無傳感器永磁同步電機的位置辨識與控制研究

劉道寬，余岳

湖南工業大學，湖南株洲，412007

0 引言

隨著我國社會各方面的發展進步，人們的生產生活需求越來越復雜化，使得各種類型的電機被不斷設計制造應用于人們的生產生活中。在工業領域以及人們日常生產中常用的電機類型有永磁電機、步進電機以及直線電機等。在諸多類型的電機中，永磁同步電機由于其體積小、重量輕的特點在我國各領域被廣泛應用，而且發揮著極其重要的作用。隨著各項技術的發展進步，永磁同步電機在制造過程中各項性能都有所提升，但是相對于應用過程中對其性能的需求還是有所欠缺。在永磁同步電機的發展中，大多數研發者以及用戶都將降低控制系統的成本作為當前的發展目標，并且有很多學者對于永磁同步電機的控制提出了各種方式和策略，取得了一定的成果。在永磁同步電機的發展中，轉子位置的獲取是非常關鍵的問題之一，以往的檢測方式是通過傳感器技術實現的，例如應用較多的霍爾傳感器以及相應的光電編碼器等機械傳感器系統，但是在應用過程中存在一定的問題。為了避免傳感器系統應用過程中存在的各種問題，本文對無傳感器的永磁同步電機控制進行了簡單的介紹，旨在提升永磁同步電機的動態控制性能。

1 永磁同步電機的控制策略

1.1 恒壓頻比控制

同步電機在運行的過程中，其轉速與電機定子電流的關系為固定的比值，在永磁同步電機轉速調節控制的過程中，通常采取的措施是調節電機輸入側的電壓頻率。電機運行效率的關鍵是其氣隙磁通是否能夠保持在恒定的值，若電機的氣隙磁通能夠維持在特定的值，則電機的效率就能處在最高狀態下且不會使磁路處于飽和狀態[1]。之所以稱之為恒壓頻比控制就是要使電機定子端的電壓與其定子側的供電頻率的比值始終保持為一個不變的常數，體現在實際運行中就是要保持基頻狀態下的氣隙磁通保持恒定不變值。若要在高于基頻頻率的狀態下進行調速，從額定供電頻率往上就會有一定的提升，但是由于電機運行的逆變器通常對輸出電壓有一定的要求，所以端電壓的值最高只能穩定在額定電壓的狀態下，造成的結果就是電機的氣隙磁通以及運轉頻率反向降低。此類控制方式無法對電機的轉矩進行有效的控制，在當前電機的控制中已經很少應用。

1.2 直接轉矩控制

直接轉矩控制是通過控制電機的電磁轉矩從而實現電機轉速以及位置的控制。在同步電機的逆變器上施加一定的電壓能夠在一定程度上改變電機的轉矩，使其相應地增大或者減小，電機的氣隙磁鏈也會發生相應的變化。不含電流環是同步電機直接轉矩控制的特性，所在實際控制中也不需要坐標變換的環節，在普通三相靜止的坐標系中就能夠進行正常的控制[2]。在目前的應用中，直接轉矩控制已經被廣泛應用于永磁同步電機的調速系統中。但是在應用過程中發現，此控制方法應用在電機運行過程中，會使電機轉矩以及磁鏈發生明顯的波動，而且由于沒有電流閉環，所以需要考慮電機過流的問題。

1.3 神經網絡控制

神經網絡控制是現在控制體系中應用較為廣泛的控制方法，其控制方式能夠很好地解決控制條件較為復雜的控制過程，例如在生產過程中常見的非線性控制系統或者一些不確定的控制系統，神經控制系統都能夠起到良好的作用。在傳統的電機控制體系中，通常都是在電機數學模型的基礎上進行數字推導從而制定電機的控制方案。但是神經網絡控制在同步電機的應用中打破了傳統意義上的控制過程，其控制方式具有較強的魯棒性，能夠有效避免一些電機參數對控制效果的影響。由于神經網絡的控制體系較為復雜，所以在實際運行過程中，需要進行大量的計算，這就導致對電機的控制芯片以及各種控制電路的要求相對較高，成本相對來說也較高，但是神經網絡控制在當前的發展中仍然有很大的提升空間。

1.4 永磁同步電機無傳感器控制

隨著電力電子技術的進步，電力電子技術在永磁同步電機領域的應用越來越廣泛。由于傳感器控制的電機在某種工業環境下的應用存在一定的局限性，所以無傳感器控制的技術成為當前永磁同步電機控制的關鍵領域。此控制方式的關鍵就是不采用傳統意義上的傳感器，而是通過計算機算法的應用來估算電機轉子的位置以及轉速。對于電機的不同轉速，永磁同步電機通常需要采取不同的控制方式，而控制方式的選擇主要取決于電機的反電動勢以及相應的轉速之間額關系，在測量電機轉子相應信息的過程中，反電動勢是其必要的條件之一。在電機啟動時，或者轉子以較低的速度運行時，電動勢的值會非常小，計算機在提取相應信息的過程中就會很艱難，所以在這種情況下，就需要通過利用控制算法來增強信息提取的效果。通常無傳感器電機在不同轉速下有著不同效果，其控制方式通常有以下幾種。

（1）高頻注入法。永磁同步電機由于自身磁鋼安裝方式的不同，會使自身的凸極效應存在很大的差別。若是永磁同步電機的磁鋼安裝在電機的內部，這種情況電機的d軸以及q軸的電感大小不一，電機d軸的電感小于q軸的電感。由于d、q軸的電感大小不一，所以電機本身就會具有凸極效應，能夠測得需要的變量信息[3]。但是如果磁鋼安裝在電機的表面，就會使得電機的d、q軸存在同樣大小的電感，從而造成電機自身不能夠產生凸極效應，在這種情況下就需要利用其他的算法促使其產生凸極效應，為變化量的求解奠定基礎。高頻注入法是在電機自身或者人為通過一定的方法使其產生凸極效應，與電機自身的其他要素沒有關系，在實際應用中，高頻信號注入法分為旋轉高頻注入以及脈振高頻注入兩種方式。

（2）直接計算法。直接計算法的特點是實施的過程相對較為簡單，動態響應的速度較快。直接計算法的原理就是利用永磁同步電機定子端電壓與電流的關系，從而計算出電機轉子的位置以及相應時間的轉速。

（3）擴展卡爾曼濾波法。擴展卡爾曼濾波法在非線性系統的控制中應用非常廣泛，而且其在應用過程中能夠在一定程度上抑制系統中存在的誤差，計算的精度相對較高，但是在實時性方面就存在一定的欠缺。

2 滑模變結構控制原理

2.1 滑模變控制原理分析

永磁同步電機實現無傳感器控制主要是建立在滑模變結構控制原理的基礎上，實現對電機位置以及轉速的控制，有著較強的魯棒性。

在滑模變控制理論的基礎上，我們分析滑動模態的定義以及其數學表達式，通常情況下，在滑模變控制系統中，有：

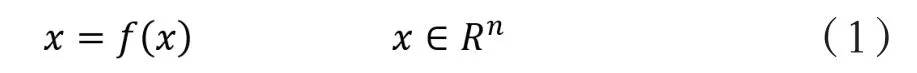
在公式（1）里有s(x)=s(x1,x2,…xn)，從而使得狀態空間分為兩部分，分別為s>0與s<0兩部分，三種情況的分布如圖1所示。

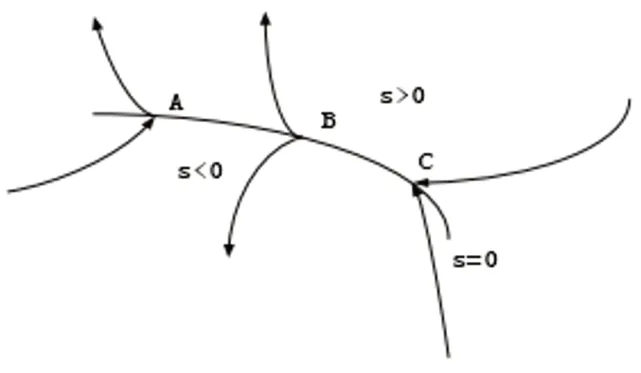
圖1 情況分布圖

對于以上三種情況，A點為通常點，B點為起始點，C點為終止點，對于A點來說，當運動點到達s=0的情況下，則會穿過；對于B點來說，當運動點到達s=0的情況下，則會從兩側離開；對于C點來說，當運動點到達s=0的情況下，會從兩邊運動到該點

在實際滑模控制中，對于前兩種情況下并沒有什么實際的意義，最關鍵的就是第三種情況。在實際控制過程中，如果所有的點都會運動到第三種情況下，就會停留在C點附近運動。所以，通常切換面s=0都是終止點的空間，通常成為滑動模態區域，在這一區間內的運動稱為滑模運動。

在點運動的過程中，若點在s=0的附近，可以通過以下數學表達式進行表示：

或者可以將以上表達式表示為：

對以上的表達式的約束下會對滑模控制提出李雅普諾夫函數的必要條件，有以下的表達式：

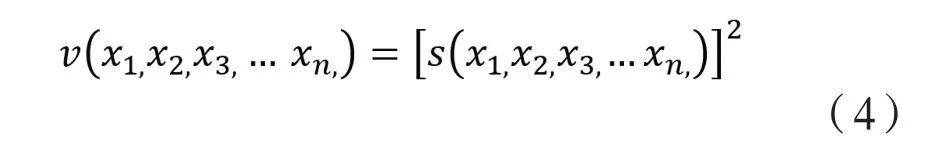
上述式子是正定的，在上述約束條件的限制下，s2在求導后得到的導數通常為負半定的情況，所以在s=0的附近v函數通常是一個單調遞減函數或者是函數值維持不變，在滿足上述條件約束的情況下，系統通常會穩定在s=0的狀態下。

對于滑模變控制階段的定義，我們可以通過以下的方式進行定義，首先假設：

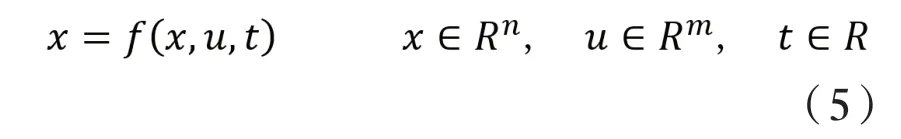
以數學表達式進行切換函數的表示為：

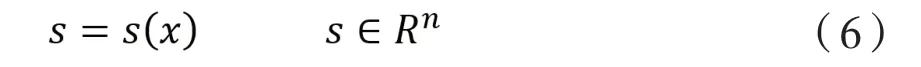
控制規律的數學表達式為：

在永磁同步電機的滑模變控制中，若滿足以上條件，理論上能夠實現電機的滑模控制，在永磁同步點擊滑模變控制過程中，s(x)與u(x)的選擇是保證運動點是否能夠快速進入滑模面的關鍵，對永磁同步點擊的控制性能的提升非常重要。

2.2 滑模變結構控制的抖振問題

在通過滑模變結構控制電機運轉的過程中，通常情況下外界環境的變化或者電機運行參數的調整并不會對控制系統產生較大的影響，抗干擾以及自我恢復能力較強。滑模變控制結構導致電機抖振是因為滑模變控制結構并不采用連續的函數以及受電機開關特性的影響，當電機處于高速運行的狀況下，則會發生抖振現象。抖振現象的存在會在一定程度上影響控制的穩定性。但若采取相應的方法消除抖振現象則會影響系統的抗擾動能力，所以電機在運行過程中不可能完全消除諧振現象，只能通過其他方法盡可能減小抖振現象對電機控制的影響。在電機運行過程中，造成抖振現象產生的原因有以下幾方面。

（1）時間滯后開關。對于圖1中s(x)的分布情況，在s(x)附近，開關函數會存在時間滯后的情況，控制狀態的實時變化也會由于開關的時間滯后而存在延遲。

（2）空間滯后開關。和時間滯后開關相似，空間滯后開關在空間狀態上存在一定的滯后情況，開關在空間狀態上的滯后會使得空間里存在相應變量的死區。

（3）系統慣量的影響。滑模結構控制的運動，在實際運行過程中由于加速度的加速幅度是有一定限制的，同樣也會使得切換過程存在一定的滯后情況。

（4）離散系統本身的因素導致抖振。滑模結構控制在正常情況下，切換動作都會發生在圖1中的s(x)面上，但是由于離散系統滑動模態并不是非常標準，所以就可能導致切換動作并沒有在切換面上，從而導致產生衰減形式的抖振現象。

以上幾種情況都會在一定程度上導致抖振現象的產生，但是在計算機技術不斷發展應用的前提下，其不斷提升的計算能力能夠將在時間及空間上滯后的情況在一定程度上減弱。另外兩種因素是由切換過程中造成的抖振現象導致的，而加強切換動作的連續性能夠提升控制效果。

3 永磁同步電機無傳感器復合控制

滑模變結構控制永磁同步電機的運行具有良好的魯棒性，但是滑模變結構通常應用在電機處于高速運轉的情況下；對于電機處于靜止或者轉速較低的情況下時，電機的反電動勢通常很小，甚至為零，就會導致無法精確估算轉子的位置，此方法則不適用。

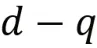
3.1 脈振高頻電壓注入法控制原理

圖2 高頻注入轉子位置估算控制框圖

向d軸注入的高頻電壓信號用數學表達式可以表示為：

實際位置角θ、位置估算角θ1與差值的關系如圖3所示。

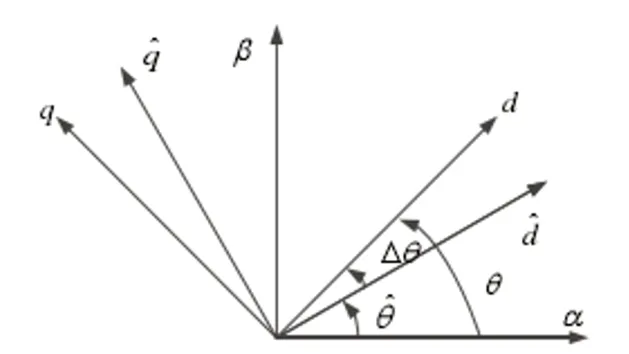
圖3 各坐標關系圖

3.2 永磁同步電機位置辨識

永磁同步電機的轉速范圍相對較寬，為了能夠在寬轉速范圍內實現有效控制[5]，需要結合電機高轉速情況下的滑模控制算法，通過加權系數法實現不同方法之間的有效切換，加權系數法如圖4所示。圖中所示的K1、K2分別表示不同估算速度下的加權系數，ω1、ω2分別表示不同切換方法的臨界速度。當ω<ω1時，電機處于低速運行的狀態，需要通過高頻注入信號來測量電機轉子的位置信息，此時，加權系數K1=1，K2=0。當<ω<ω2時，此時的估算速度為ω=K1ωHF+K2ωSM0，此種狀態下的估算轉速呈線性關系。當ω>ω2時，電機處于高速運行的狀態，此時轉子位置的檢測就需要采用滑模控制法，此時的加權系數K1=0，K2=1。

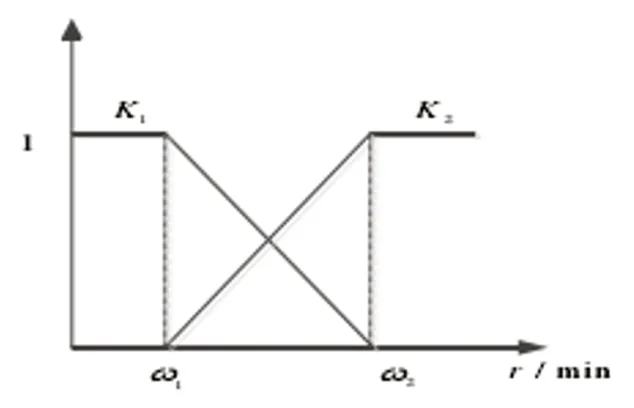
圖4 加權系數法

在永磁同步電機的位置控制中，臨界速度ω1、ω2的選取需要滿足一定的條件，在保證滿足電機能夠處于低速運行的狀態下，滑模變控制法能夠穩定運行的最低轉速要在臨界速度ω1以下，同時，還需要保證電機處于轉速較高的狀態時，低速算法運行的穩定速度要在臨界速度ω2以上。控制系統的結構框圖如圖5所示。

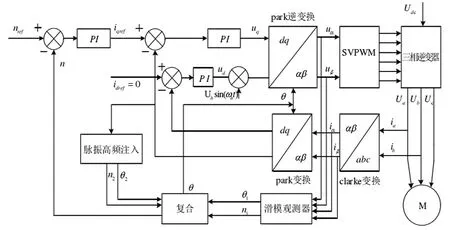
圖5 電機位置辨識結構框圖

4 結語

本文對電機處于不同轉速下的情況分別進行分析，對于高轉速下的電機，可以通過滑模變控制理論進行電機轉子位置的估算控制，若電機處于低速或者靜止的狀態下，則需要注入脈振高頻電壓對電機轉子位置進行估算。在永磁同步電機的運行中，要確保其能夠穩定持續地運行，對轉子位置的精準測量控制是非常重要的。在傳統控制中通過傳感器控制通常受環境的影響較大，且會增加電機運行的成本，所以對永磁同步電機的無傳感器控制是非常重要的。