基于深度學習的微生物高階邏輯關系分析方法

劉芃蘭，孫碩男

（遼寧工程技術大學電子與信息工程學院，葫蘆島 125105）

0 引言

整個生物圈存在著多種多樣的微生物，從海洋湖泊、土壤大氣到人體的口腔腸道都有微生物的存在。在自然界，不同類群的微生物能在多種不同的環境中生長繁殖，它們彼此聯系、相互影響。微生物復雜的生命活動和相互作用對于微生物群落的動態和功能起著重要的作用。

越來越多的證據表明物種間不僅存在成對的相互作用，也存在諸如循環交叉進食和集體共生等大量的高階相互作用，這些高階相互作用不但可以使得競爭網絡達到動力學穩定，而且對于研究新物種引進也具有重要意義。Zelezniak 等使用基因組尺度的代謝建模方法，系統地調查了超過800個社區的資源競爭和代謝交換的程度，對于所有可能的兩個、三個和四個物種組合的子群落，使用Fisher精確檢驗來評估共現關系的顯著性，從而解釋了涉及兩個以上物種的高階相互作用的可能性。Bairey 等通過模擬隨機交互作用下群落的動態，發現兩兩相互作用對增加的物種敏感，而四項相互作用對刪除的物種敏感，它們共同產生了物種數量的上限和下限。實驗結果進一步表明物種互作通常是以高階組合的形式發生的，兩個物種間的相互作用通常由一個或多個其他物種調節，這些高階相互作用對自然生態系統多樣性十分重要。

傳統計算模型大多通過成對關系構建微生物網絡。然而，由于微生物關系復雜多變，這種成對網絡構建方式可能會遺漏大量高階相互作用，不能很好地捕捉微生物網絡的本質特性。網絡基序是一種小巧、重復且保守的生物網絡單位，它是一個至少包含三個節點且常常出現的網絡子圖，在網絡中執行各種計算任務，通常被理解為一種高階功能結構。基于這些網絡基序來構建高階網絡結構，有助于微生物高階關系的挖掘，并促使人們更好地理解微生物的功能。識別網絡模塊是執行網絡分析的重要途徑，高模塊性表明網絡在某些節點組內具有密集連接，并且模塊之間的連接稀疏。Girvan 等根據社區具有高內聚、低耦合的屬性提出基于中心指數來尋找社區的算法。Benson 等提出張量譜聚類算法，根據網絡集群中指定的高階網絡結構，開發多線性譜方法對網絡進行聚類。Perozzi 等提出了一種Deep-Walk 模型，該模型通過一種截尾隨機游走的均勻采樣模型將未加權圖轉化為線性序列集合，然后利用Mikolov 等提出的跳躍圖模型從這些線性結構中學習頂點的低維表示，實驗結果表明，該模型在聚類任務中要優于常用的譜聚類和模塊度模型。基于微生物的縱向數據，Shen等利用動態貝葉斯模型（DBN）構建微生物的加權有向網絡，然后利用加權基序和未加權基序對網絡的高階結構進行分析。聚類結果表明，加權基序可以獲得更好的聚類。Yu 等提出了一種基于類內散射矩陣的超圖聚類方法，并利用譜聚類來實現社區探索，結果表明該方法在一定程度上可以有效地挖掘微生物的高階模塊。

本文提出了一種基于深度學習的超圖聚類模型（hypergraph clustering model based on deep learning,DeepHC），用于挖掘微生物的高階邏輯關系，該模型基于人體18 個部位的微生物豐度數據，計算滿足要求的8種邏輯類型的分布，并選取最普遍的邏輯類型來構建高階微生物網絡。針對簡單圖聚類方法不能有效挖掘高階關系，而網絡的線性嵌入不適用于復雜非線性關系挖掘的問題，提出了一種基于深度神經網絡的超圖聚類模型，該模型通過計算偏移正點態互信息矩陣來獲得更為準確的網絡表示，通過深度堆疊自編碼器來獲得樣本的非線性低維表示，并利用最大模塊度聚類來自適應挖掘微生物的高階模塊。與其他方法的對比結果表明，DeepHC 得到的微生物模塊具有更好的類內緊湊性和類間分離性，可以作為微生物高階模塊挖掘的有效工具。

1 數據與解決方案

1.1 數據

人類微生物組計劃研究了大量的微生物群落數據，可以用來描述與人類相關的微生物群落的生態學特征。本文從HMP 數據庫中下載16s RNA 序列數據，并經過Mothur 處理得到了V13高質量文件，涵蓋了5個人體區域（Gastrointestinal tract，Oral，Skin，Airways，Urogenital tract）的18 個部位，包括3242 個樣本，606 個微生物的豐度數據。Gastrointestinal tract 區域有214 個樣本，包含1 個部位Stool；Oral 區域有1807 個樣本，包含9 個部位，分別是Attached Keratinized， gingiva，Buccal mucosa，Hard palate， Palatine Tonsils， Saliva， Subgingival plaque，Supragingival，plaque，Throat，Tongue dorsum；Skin 區域有736 個樣本，包含4 個部位，分別是Left Antecubital fossa，Left Retroauricular crease，Right Antecubital fossa，Right Retroauricular crease；Airways 區 域 有188 個 樣 本，包含1個部位為Anterior nares；Urogenital tract區域有297個樣本，包含3個部位，分別是Mid vagina，Posterior fornix，Vaginal introitus。上述數據可以從http://hmpdacc.org/HMMCP/下載。

1.2 解決方案

本文提出的DeepHC 方法包含3 個步驟（如圖1 所示）。首先，從微生物豐度數據中計算八種邏輯關系，并提取最多的邏輯類型來構建微生物高階邏輯網絡（如圖1 的step1）。其次，構建加權超圖模型，并通過超圖約簡得到微生物的連接網絡（如圖1 的step2）。最后，提出了一種基于深度神經網絡的聚類模型用于微生物模塊挖掘（如圖1的step3）。

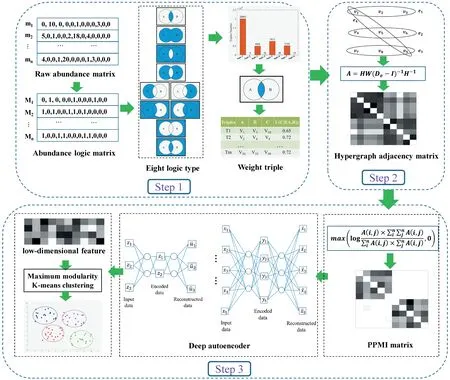
圖1 基于DeepHC的高階邏輯關系分析框架圖

2 模型與方法

2.1 高階邏輯關系提取

不確定性推理已被廣泛應用到機器學習、專家系統、智能決策等領域，概率邏輯是一種常用的不確定推理方法，它在原有邏輯研究的基礎上進行一些概率推理，將概率論和邏輯表示完美融合。微生物的相互作用是群落結構的驅動因素之一，群落中物種的非隨機分布可以用來推斷這些相互作用。基于微生物豐度數據，本文將概率邏輯應用到微生物領域，進而挖掘微生物的高階交互關系。

首先，對微生物的原始豐度矩陣離散化處理。當微生物在樣本中的豐度值(,) ＞0，則對應的(,) = 1；否則，(,) = 0，刪除∑m(,) ＜4的記錄。經過以上操作，可以獲得最終的微生物豐度邏輯矩陣。

其次，計算任意三種微生物間的不確定系數(|)、(|) 和邏輯組合譜(|(,))。對于任意隨機變量和，(|)的計算方法如下：

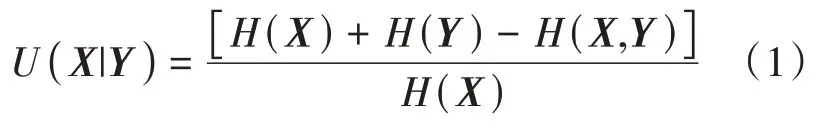
其中，()和()分別表示和的獨立分布信息熵，(,)表示和聯合分布信息熵。由式（1）可知，(|)∈[0,1]，當完全由確定時，(|)= 1；當和完全獨立時，(|)= 0。因此，對于任意微生物三元組{,,}，(|)和(|)表示微生物和的個體對微生物的影響， 對應成對關系；(|(,))表示微生物和的邏輯組合對微生物c 的影響，對應高階關系。本文中，(,)表示微生物和的8 種邏輯組合。本文選擇成對關系較弱，而高階關系較強的三元組，即選擇滿足條件：{（,,）|（|）＜0.4,（|）＜0.4,（|（,））＞0.6}的所有三元組。然后，統計18個部位中不同邏輯類型下三元組的發生情況，結果如圖2所示。

從圖2 可以看出有5 個部位（‘Right Antecubital fossa’，‘Left Retroauricular crease’，‘Left Antecubital fossa’，‘Right Retroauricular crease’，‘Anterior nares’）滿足要求三元組的總數大于2000，并且這些部位的邏輯類型‘=∧’占據絕對的優勢，即當和共同存在時，也存在。因此，基于邏輯類型‘=∧’，利用部位‘Right Antecubital fossa’，‘Left Retroauricular crease’，‘Left Antecubital fossa’，‘Right Retroauricular crease’，‘Anterior nares’中的所有三元組來構建高階交互關系。

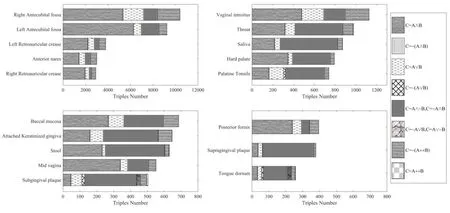
圖2 18個人體部位的8種邏輯類型的三元組統計圖

2.2 超圖構建

圖聚類根據節點之間的成對相似性對節點集進行劃分。然而，由于微生物的多樣性，且多樣性的社區很大程度依賴于高階相互作用的穩定程度，因此研究微生物的高階相互作用對理解微生物群落的多樣性和穩定性具有重要意義。Agarwal 等首先認為聚類問題是超圖劃分的一個實例，該方法首先利用一個加權圖來逼近超圖，然后利用譜聚類算法來進行超圖的節點劃分。Zhou 等將譜圖聚類技術推廣到超圖，提出了一種超圖歸一化切割準則，得到一種歸一化超圖切割的聚類算法。

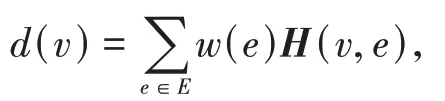
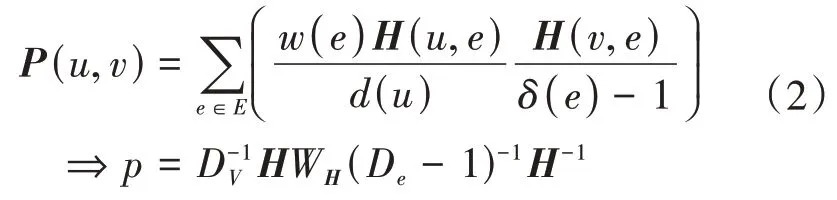
將式（2）與隨機游走的公式=對照，可以得到微生物間的連接矩陣：

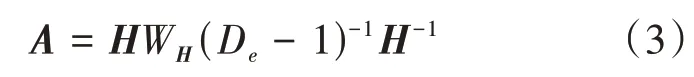
進而，可得超圖拉普拉斯矩陣為：=1-DAD。

2.3 基于深度神經網絡聚類

基于微生物的拉普拉斯矩陣，傳統的譜聚類利用奇異值分解（SVD）和均值可以得到最終的聚類結果。在此過程中SVD 起到降維的作用，通過線性投影將原始表示空間映射到一個新的低秩表示空間。然而，由于實際問題的復雜性，線性投影可能會損失重要的信息。

Tian等利用稀疏自編碼器來代替譜聚類中的SVD，取得明顯的改進，在此基礎上，Cao等提出了一種深度神經網絡模型（deep neural networks for learning graph representations,DNGR）來學習圖的表示，該模型首先利用隨機沖浪模型直接捕捉圖形結構信息，然后利用偏移正點態互信息（positive pointwise mutual information,PPMI）模型來增強圖的魯棒性，最后引入疊加去噪自動編碼器來提取復雜的非線性特征。DNGR模型在很多聚類和圖表示問題中都取很好的效果。盡管DNGR 利用隨機沖浪通過轉移矩陣的迭代可以挖掘更多的間接交互，然而該過程也在一定程度上增加部分噪聲，同時傳播參數的選擇也增加模型的復雜性。基于以上分析，本文利用PPMI 來增強網絡表示，同時利用堆疊自編碼器來挖掘樣本的低維特征，最后利用均值聚類來計算聚類結果。首先，基于微生物的連接矩陣，計算偏移正點態互信息矩陣PPMI來產生網絡表示。PPMI 矩陣構建方法如下：

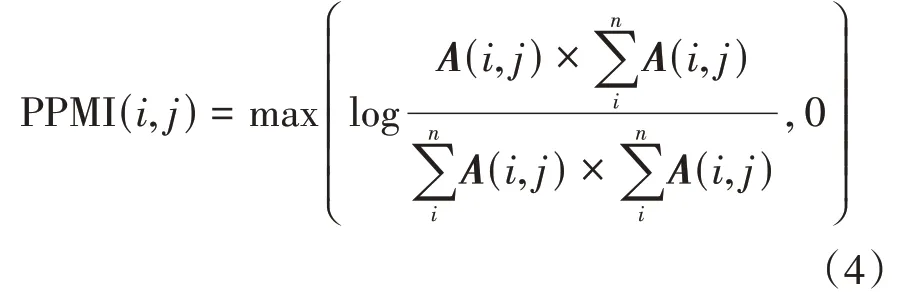
由式（4）可看出，該計算過程保證PPMI 中元素的非負性。

然后，挖掘微生物的非線性低維表示。利用堆疊自編碼器從PPMI 矩陣中產生壓縮的、低維的向量表示，這個過程執行了從高維向低維的映射。自編碼器包含兩個步驟，編碼步驟和解碼步驟。在編碼步驟，函數（·）應用到輸入向量，并將其投影到新的特征空間。解碼步驟，重構函數（·）從潛在表示空間來重構原始的輸入向量。假定：（·）=（+），（·）=（+），其中（·）是激活函數，={,}表示編碼步驟的權重參數，={,}表示解碼步驟的權重參數，和表示從輸入空間到輸出空間的線性投影，和表示偏置向量。目標是通過找出和來最小化如下的重構損失函數：

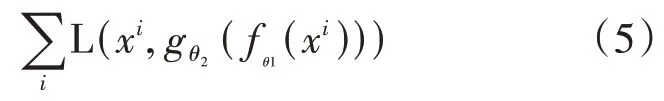
其中，L 表示樣本損失函數，x表示第個樣本。在這個過程中，激活函數通常用來建模輸入空間到輸出空間的非線性關系。堆疊自編碼器是由多層這樣的自編碼器組成的深度神經網絡，它使用分層的訓練方法來提取基本規律，從數據層逐層捕獲不同層次的抽象，高層從數據中傳遞更高層次的抽象。通過執行以上過程，可以得到樣本的低維特征表示。

最后，利用最大模塊度進行類別數選擇。基于堆疊自編碼器得到的樣本低維特征，利用均值可以得到最終的聚類結果。然而，在此過程中聚類數的選擇也是個問題。模塊性表現為模塊內部的節點比較稠密，模塊間的節點比較稀疏。模塊性是生物網絡的重要特性，研究生物網絡的模塊性有助于理解復雜的功能和特性。超圖模塊度是簡單圖模塊度在超圖中的推廣，令（,）表示頂點和頂點的期望邊數，其計算方法如下：

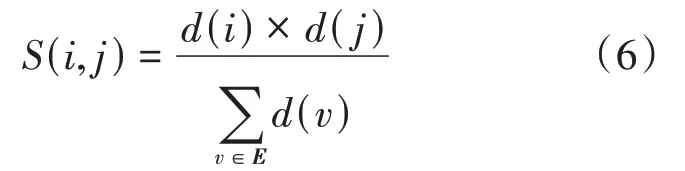
其中，（）表示加權超圖中頂點的度。令超圖模塊化矩陣為A-S，此時，對于任意的聚類結果，可以得到超圖的模塊度，如下式所示：

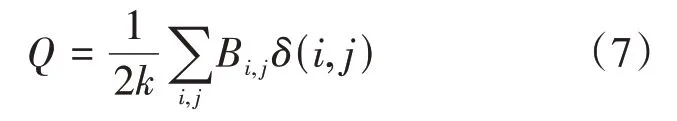
其中，表示類別數，（·）表示聚類指示函數，即當頂點和頂點為同一個類別時，（,）=1；否則（,）=0。本文計算不同聚類數下的模塊度，并選取最大模塊度對應的聚類數。

3 性能與實驗分析

3.1 模型評估

3.1.1 RMSSTD指標

RMSSTD是用來衡量聚類結果的同質性，即緊湊程度。它指的是所有類內樣本方差的平方根，具體計算公式如下：

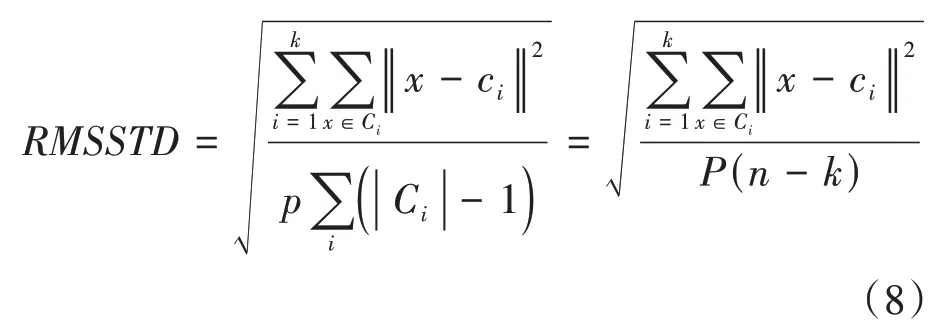
其中，表示類別數，表示樣本點，C表示第個聚類的樣本集合，c表示第個聚類集合的中心， ||C表示C中樣本總數，表示樣本的維度。由上式可以看出，越小，類內樣本的方差越小，類內樣本的緊湊程度越小，聚類效果越好。

3.1.2 RS指標

RS 指標用來評估類間差異程度，即分離程度。它用來衡量一個類別與其他類別的區分度，具體計算公式如下：

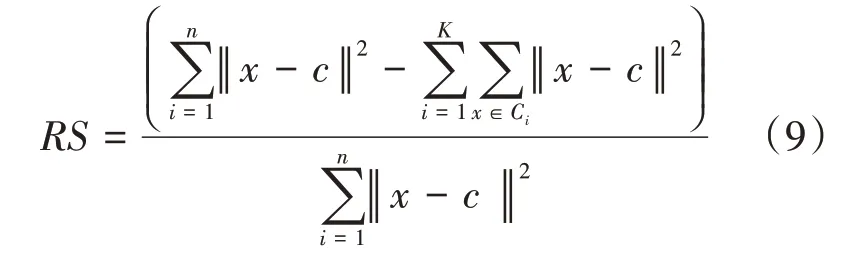
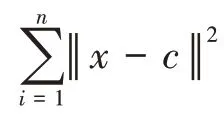
3.1.3 CH指標

CH 是一種常用的內部聚類評估指標，由Calinski 等提出，基于類間距離和類內距離的平方和來評估聚類有效性。具體計算公式如下：

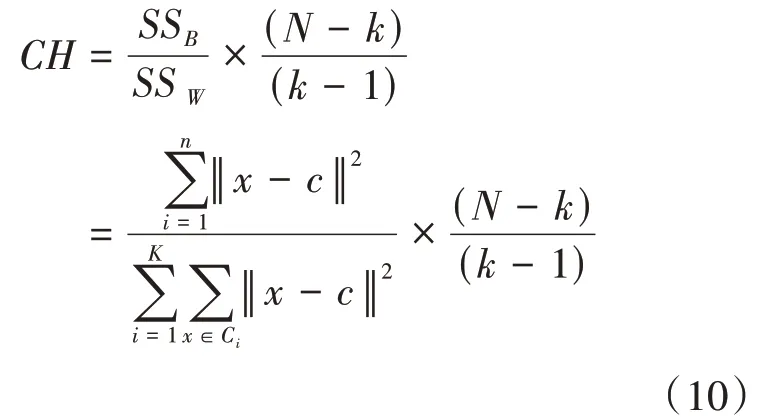
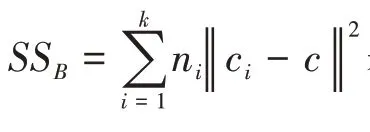
3.2 實驗設置

為了全面評估模型的性能，實驗選擇3種對比模型，分別是未加權的超圖譜聚類模型（HSC）、加權超圖譜聚類模型（HCWS）和基于類內散度的超圖聚類模型（HCIS）。對于HSC，超邊權重矩陣W為單位矩陣，即所有超邊的權重為1，并通過譜聚類得到聚類結果。對于HCWS，超邊的權重為邏輯組合譜(|(,))，并利用譜聚類計算聚類結果。對于HCIS，按照論文的原始方法來計算結果。對于DeepHC（本文方法），利用3 層自編碼器來生成堆疊自編碼器，每層輸出樣本的維度分別為100、50、10。關于模型的評估，由于所有方法都是基于豐度邏輯矩陣執行的，因此根據和每個模型的聚類結果計算評估指標。此外，為了消除偶然因素對結果的影響，本文將每個實驗執行50次，并將評估指標的均值作為最終的結果進行評估。

3.3 結果對比

關于人體的五個位點（‘Left Antecubital fossa’，‘Right Retroauricular crease’，‘Left Retroauricular crease’，‘Right Antecubital fossa’和‘Anterior nares’），基于利用邏輯類型1 提取高階邏輯關系，將本文模型（DeepHC）與HSC、HCWS和HCIS 的聚類結果進行對比。表1 展示部位‘Left Antecubital fossa’和‘Right Antecubital fossa’，四種計算模型關于三種指標的結果對比。

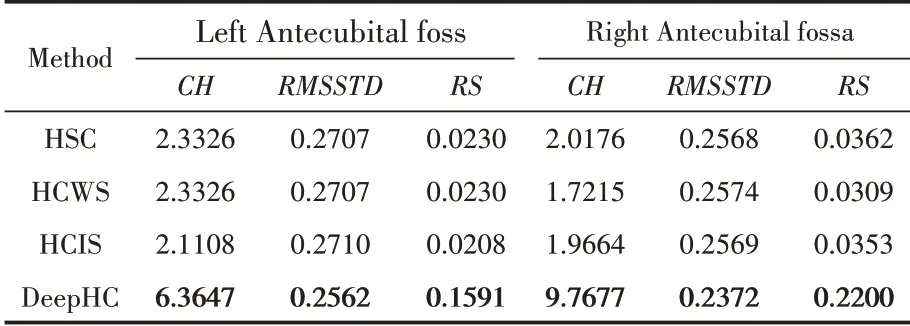
表1 Left Antecubital fossa和Right Antecubital fossa的聚類結果對比

從表1 可以看出，無論是類內緊湊度指標（RMSSTD）、類間差異性指標（RS）還是綜合評估指標（CH），本文的模型（DeepHC）關于部位‘Left Antecubital fossa’和‘Right Antecubital fossa’的聚類結果均更好。具體來講，關于部位Left Antecubital fossa，DeepHC 的RMSSTD 指 標為0.2562，小于其他模型，說明DeepHC 類內樣本的緊湊程度更好；DeepHC 的指標為0.1591，遠大于其他模型，說明DeepHC 類間差異程度更大；DeepHC 的CH 取值為6.3647，相對于HSC、HCWS 和HCIS 的2.3326、2.3326 和2.1108 分別提升172.86%、172.86%和201.53%，進一步說明DeepHC 具有更好的聚類效果。關于Right Antecubital fossa，DeepHC 的RMSSTD 指標為0.2372，小于其他模型；RS和CH指標分別為0.2200和9.7677，遠高于其他模型，進一步說明DeepHC 具有更高的聚類質量。對于剩余的三個部位‘Left Retroauricular crease’，‘Right Antecubital fossa’和‘Anterior nares’，本文將每個部位的指標歸一化處理，并將結果以堆疊柱狀圖的形式展示出來，如圖3所示。

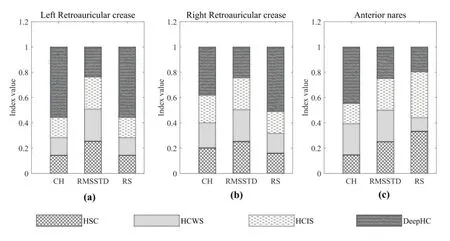
圖3 位點‘Left Retroauricular crease’，‘Right Antecubital fossa’和‘Anterior nares’的聚類結果對比

由圖3 可以看出，對于這三個部位，DeepHC 幾乎各個指標都取得了最好的結果。對于部位′Left Retroauricular crease′，如圖3（a）所示，DeepHC 的指標最小，對應類內樣本的緊湊程度最好；RS指標最大，說明DeepHC類間差異程度更大；同時綜合指標HC 也最大，說明DeepHC 取得了最好的聚類結果。關于部位‘Right Antecubital fossa’，也得到了同樣的結論。對于部位‘Anterior nares’，DeepHC 除了RS 指標不是最優之外，RMSSTD 和HC 指標都是四個模型中最優的。以上結果表明，DeepHC 可以作為微生物高階模塊挖掘的有效工具。

4 結語

本文提出了一種基于深度學習的超圖聚類模型來分析微生物的高階邏輯關系。與傳統的根據微生物成對相關性構建網絡的方式不同，本文選擇那些兩兩關系較弱，而聯合關系較強的高階關系進行分析，并統計八種邏輯類型在人體18 個部位的分布，利用出現最頻繁的邏輯類型來構建高階網絡。針對一般聚類模型或者不能很好挖掘樣本間的高階關系（簡單圖聚類），或者僅適應于具有線性關系的樣本集合（基于SVD 的譜聚類模型），本文提出了一種基于深度學習的超圖聚類模型，該模型通過計算偏移正點態互信息矩陣來增強圖的表示，通過深度神經網絡來挖掘樣本的低維非線性表示，通過基于模塊度的K 均值聚類來自適應地選擇聚類個數。實驗結果表明，本文提出的DeepHC 具有更好的聚類效果，可作為微生物的高階邏輯關系分析的有效工具。