面向亞軌道解體事故的碎片擴散分布建模研究
陳萬通, 田書雨, 張巨聯, 劉 慶, 任詩雨
(1. 中國民航大學民航航班廣域監視與安全管控技術重點實驗室, 天津 300300;2. 中國民航大學電子信息與自動化學院, 天津 300300;3. 上海飛機設計研究院, 上海 201109; 4. 上海航天電子技術研究所, 上海 201109)
0 引 言
近年來,伴隨著航天活動驅動者由政府為主轉向市場為主,商業航天成為全球航天活動的重要驅動力,亞軌道飛行的商業化進程發展迅速。與民用航空飛行方式不同,亞軌道飛行是介于萬有引力和空氣動力雙重作用下的飛行,由于未達到繞地飛行速度,飛行器相當于在太空中做個拋物線運動回到地球(最高點一般高于卡門線)[1-2]。相比于普通的航班,亞軌道飛行時間會縮短數倍;相比于飛船,亞軌道飛行器造價低廉且可重復使用,因此呈現出巨大的經濟價值。其中,以美國縮尺復合體公司與英國維珍銀河公司聯合研制的“太空船”、美國藍色起源公司的“山貓”、瑞士空間系統公司的“亞軌道飛機可復用”飛行器[3]為代表性的亞軌道飛行器已開展多次亞軌道飛行試驗。據權威機構預測:亞軌道交通運輸極有可能成為下一代空天旅行的主要方式之一[4]。
亞軌道飛行器以高超音速飛行,在強烈的氣動載荷作用下易發生解體并產生大量碎片,碎片在大氣環境中所受的氣動力呈現一定的隨機性,其分布和落點較難預測,一旦與民航客機發生碰撞,將瞬時產生災難性后果。全世界對亞軌道事故碎片碰撞風險的廣泛關注始于2003年美國哥倫比亞號航天飛機失事事件,碎片橫貫美國德克薩斯州1 000 km×40 km的陸地范圍,覆蓋人口21.6萬[5]。2018年6月30日,日本星際科技公司于北海道航天試驗基地試射自行研制的Momo2小型亞軌道火箭,升空后不久發生爆炸;同年11月28日韓國在亞軌道發射試驗中,火箭飛行10 min后部分殘骸意外落入日本沖繩島海域,引發日本民眾強烈抗議。據美國聯邦航空管理局(Federal Aviation Administration, FAA)計算,任何超過300 g碎片的撞擊都將導致商用飛機100%的損毀,不足300 g的碎片如果撞擊到較脆弱的機身區域,例如飛機操縱面或燃油箱,也將導致被撞飛機損毀的嚴重后果[6]。
為了保障航天器的在軌安全,國內外對空間碎片的研究已經長達數十年,研究內容涵蓋了空間碎片的模型和風險分析[7-8]、碰撞預警與規避策略[9]、軌道碎片環境建模[10]等多個方面。然而,空間碎片理論主要針對外層空間,重點關注空間碎片對在軌航天器的碰撞損傷,不涉及地面安全風險。繼哥倫比亞號事件之后,飛行器因解體事故產生的亞軌道碎片引起了全世界廣泛關注。相比于空間碎片的研究,亞軌道碎片與地面人群的安全利益、財產利益直接相關。國外用來預測亞軌道碎片位置的軟件主要包括法國的發射和再入安全評估工具ELECTRA?[11]、美國國家航空航天局(National Aeronautics and Space Administratio, NASA)的通用實時碎片足跡(common real time debris footprint, CRTF)[12]、美國APT公司的碎片風險評估(debris risk assessment, DeBRA)[13]、斯坦福大學的靶場安全評估工具(range safety assessment tool, RSAT)[14]、FAA開發的航天飛機危險區域計算(shuttle hazard area to aircraft calculator, SHAAC)工具[15]。上述軟件涉及專有的源代碼,僅限特殊用戶群體使用。
在亞軌道碎片分布建模方面,文獻[16-18]根據哥倫比亞號事件的碎片分布統計數據,將亞軌道碎片危險區近似等效為矩形,矩形長度為解體高度除以1 000,矩形寬度為長度的1/8,但這種近似較為粗糙,缺乏嚴謹的科學論證,不具有普遍意義;文獻[19]在亞軌道事故DeBRA的可視化仿真系統中,采用了軌跡分析模型(trajectory analysis program, TAP)仿真碎片分布,但該模型是針對航空特技表演中飛機發生意外解體事故時,對碎片的散布范圍進行預測,本質上不適用于亞軌道解體事故碎片的分布研究;文獻[20-21]利用不同協方差傳播算法對空間碎片再入解體過程中碎片的傳播軌跡進行預測,但目前只適用于單個碎片求解,對影響碎片傳播過程的關鍵因素,如彈道系數、阻力系數等缺乏詳細闡述,碎片預測模型不能滿足民航對安全性的高要求。
綜上所述,亞軌道碎片分布建模是實現危險區預測的關鍵技術,而有效的危險區預測是實施安全的空中交通管制的前提。本文在協方差傳播算法的基礎上,對亞軌道飛行器的解體模型進行建模,對解體碎片數量、尺寸分布以及阻力系數等關鍵因素進行統計分析,將有效提高碎片危險區的預測準確度,使空中交通管制人員能夠在碎片下落到達民航飛行高度之前將受影響的飛機引導出危險區域,為空中交通管制人員提供安全、高效、魯棒的決策支持,解決商業亞軌道飛行活動和傳統民航之間的潛在沖突,具有良好的應用前景。
1 亞軌道碎片運動方程
1.1 坐標系建立
利用xyz坐標系表示飛行器解體瞬間碎片在站心坐標系中的位置,坐標系的原點在地球表面的(θ0,φ0)處,θ0、φ0分別表示航空器解體瞬間的初始經、緯度。x、y軸所構成的平面表示在原點處與地球相切的平面,x軸指向東方向,y軸指向北方向,z軸垂直于xy平面指向天頂方向,xyz坐標系也可稱為東北天(east-north-up, ENU)坐標系。
1.2 單個碎片擴散機理和運動模型

(1)
式中:r=[x,y,z]T和v=[vx,vy,vz]T分別表示碎片在ENU坐標系中的位置矢量和速度矢量;ω=[0,ωecosφ0,ωesinφ0]T表示ENU坐標系的角速度矢量,其中ωe=7.292×10-5rad/s表示地球自轉的平均角速度;e3=[0,0,1]T表示第三標準單位向量;Re=6.372×106m表示地球半徑;重力加速度表示為g=ge[Re/(Re+z)]2,其中ge=9.81 m/s2;aD表示與大氣密度相關的瞬時加速度,可表示為aD(t)=-1/2(ρ|vrel|vrel)/β,其中β表示彈道系數,vrel表示碎片的速度矢量v與風矢量w之差,即vrel=v-w;ξ表示由建模不確定性和干擾所引起的隨機加速度矢量。
2 碎片傳播預測算法
空中交通管制對算法的計算效率要求很高,采用傳統蒙特卡羅方法模擬亞軌道解體事故的大量碎片雖然近似程度高但運算量巨大,不能滿足空中管制實時響應的高要求。因此,可通過解析形式的概率分布模型描述亞軌道解體事故碎片的分布特征。
2.1 協方差傳播算法
定義擴充狀態矢量s=[rT,vT]T,則碎片運動方程式(1)可重新表述[23]為
(2)
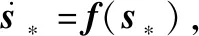
(3)
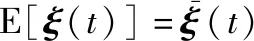
2.2 碎片概率橢球
通過引入關于時間t的由中心和形狀矩陣參數化后構造的橢球集,將碎片擴散特征的描述推廣到四維(four dimensions, 4D),由于時間變量的無限性,所得到的4D概率約束問題比三維(three dimensions, 3D)問題復雜得多。因此,解決該問題需要將時間離散化,并將每個樣本時間與一個橢球相關聯[24]。此時,單一時刻碎片的4D足跡是概率橢球的一部分,而一系列瞬時的概率橢球構成了一個“碎片通道”,碎片位置概率密度函數[21]為
(4)
(5)
式中:
(6)
其中,λ∈[-π/2,π/2],α∈[0,2π]。
3 碎片彈道系數
當亞軌道飛行器發生解體事故時,碎片的運動軌跡主要取決于彈道系數β,計算公式如下:
(7)
式中:m表示單個碎片的質量;CD表示阻力系數;A表示碎片橫截面積。接下來分別從面質比分布和阻力系數取值兩個方面來計算彈道系數。
3.1 面質比分布
亞軌道飛行器再入過程中發生解體事故時會產生大量碎片,本文采用廣泛接受的NASA標準解體模型EVOLVE4.0[25],利用該模型可以求解亞軌道碎片的質量、面質比、速度增量等關鍵參數,算法流程圖如圖1所示。
碎片的特征尺寸可表示為
(8)
式中:dx、dy、dz分別表示在三軸上的投影尺寸。對于亞軌道飛行器爆炸解體事故,解體碎片中尺寸大于dc的碎片分布數量關系可表示為
(9)
式中:cs的取值與爆炸類型密切相關,對于亞軌道飛行器解體事故來說,cs通常取值為1[26]。根據式(9)可將亞軌道碎片的尺寸分布函數表示為
(10)
在標準解體模型中,根據亞軌道碎片的特征尺寸劃分不同的區間范圍,亞軌道碎片在各個區間范圍內的面質比分布函數如下所示。
(1) 對于特征尺寸大于11 cm的亞軌道碎片,面質比分布函數可由雙正態分布方程確定:
q(λc,η)=δ(η)q1(λc)+(1-δ(η))q2(λc)
(11)
式中:λc=lg(A/m);η=lgd;δ(η)表示權系數,根據不同的解體類型確定;q1(λc)和q2(λc)表示正態分布概率密度函數:
(12)
式中:μi和σi分別表示分布函數的均值和標準差。
亞軌道碎片面質比分布函數的參數可通過下式計算:
(13)
σ1(η)=0.55
(14)
(15)
(16)
μ2(η)=-0.9
(17)
(2) 對于特征尺寸位于3~8 cm的亞軌道碎片,其面質比分布函數可表示為
q(λc,η)=q1(λc)
(18)
即權系數δ(η)=1。分布函數的參數可通過下式計算:
(19)
(20)
(3) 對于特征尺寸位于8~11 cm的亞軌道碎片,其面質比分布可通過插值的方法獲得。對于特征尺寸小于3 cm的碎片,考慮在下落過程中充分燃燒,本文中不做進一步考慮。
在亞軌道飛行器解體時刻,解體碎片獲得相對于飛行器的速度增量Δv滿足正態分布,即
(21)
式中:v=lg Δv;均值μv=0.2λc+1.85;標準差σv通常取0.4。對于亞軌道飛行器來說,考慮在解體瞬間各個碎片獲得的速度增量的方向是隨機的,其方向余弦可表示為
(22)
式中:θ1和θ2為方向角,分別在[-π/2,π/2]和[0,2π]取值區間內均勻分布。
3.2 阻力系數
亞軌道解體碎片再入過程中,努森數(Knudsen number, Kn)的大小對于計算亞軌道碎片在下落過程中所受到的空氣阻力十分重要[27],可表示為
(23)
式中:d表示亞軌道碎片特征尺寸;χ表示氣體分子平均自由程,數值大小與空氣分子的數量密度和分子大小相關:
(24)
式中:l表示空氣的分子直徑,取值為l=3.65×10-10m。N表示1 m3體積內空氣分子的總數,取值大小跟海拔高度h相關,計算公式為
N=(2.0×1025)·exp(-0.14h)+
(4.0×1017)·exp(-0.02h)
(25)
在空氣動力學中,根據Kn的大小,可劃分3個區間來計算亞軌道碎片的阻力系數,依次可劃分為連續流區、過度流區和自由分子流區。對于解體碎片,其在大氣不同流區的阻力系數CD如下所示。
(1) 在連續流區(Kn≤0.01),亞軌道碎片的阻力系數為
CD-cont=0.91
(26)
(2) 在過渡流區(0.01 (27) (3) 在自由分子流區(Kn≥1.0),亞軌道碎片的阻力系數為 CD-fm=2.1 (28) (29) 通過上述航天器標準解體模型,首先根據不同碎片的特征尺寸劃分區間范圍,確定碎片的最小特征尺寸dc,利用式(9)計算碎片總數目。然后根據分布律式(10)、式(11)、式(18)、式(21)確定解體碎片的尺寸大小、面質比、速度增量,通過采用反函數的方法對隨機變量進行抽樣取均值計算,數據統計如表1所示。 表1 標準解體模型數據統計表Table 1 Statistical table of standard disintegration model data 在此次仿真模擬中使用廣泛接受的經驗密度模型質譜儀非相干散射雷達擴展2000[29](mass spectrometer incoherent scatter radar extended 2000, MSISE-00)和水平風模型2014[30](horizontal wind model 2014, HWM14)。根據不同碎片特征尺寸和下落高度變化,計算碎片在不同高度區間內的Kn,如表2所示,根據式(26)~式(28)確定阻力系數值。在此基礎上結合表1彈道系數計算值,根據碎片特征尺寸區間將亞軌道碎片數據信息分為5組,如表3所示。利用協方差傳播算法計算碎片云的傳播軌跡,通過設置不同置信度參數分別顯示3個不同時刻的碎片傳播軌跡,如圖2和圖3所示。 表2 Kn計算表Table 2 Kn calculation table 表3 碎片數據信息分析表Table 3 Debris data information analysis table 碎片危險區邊界的劃定需要依據民航可接受的風險概率來確定。圖2和圖3分別顯示的是置信度為99.99%和95%時的橢球邊界范圍。置信度越高時,橢球邊界范圍越大,越接近真實碎片下落傳播范圍。此外,不同彈道系數值對應碎片群的下落時間也不相同,如圖4所示。彈道系數β越小,碎片下落時間越長,而β越大碎片下落的越快。 當亞軌道解體事故發生時,碎片危險區會對飛機的安全飛行造成嚴重影響,在改航路線規劃之前首先要確定碎片危險區域,碎片危險區的預測精準度將對后續改航路線的規劃產生重要影響。 本文針對亞軌道發射活動中飛行器潛在解體風險,利用協方差傳播算法來預測亞軌道飛行器在高空解體后碎片的傳播軌跡,將位置概率橢球的概念用于仿真結果的可視化。在此基礎上,參照標準解體模型,對影響碎片傳播軌跡的關鍵因素彈道系數進行推導計算,可有效提高碎片危險區的預測準確度。文章中充分考慮民航安全置信度的高要求,可通過設置置信度參數來適應民航對生命安全的風險要求,為航班規避構建安全、高效的決策支持系統。上述研究成果可以為推進民航風險防控體系建設、促進商業亞軌道飛行與民航協調一致發展提供技術參考。4 仿真結果分析




5 結 論

