一種基于神經網絡的離散傅里葉矩陣重構方法研究
黃權,阮建高
(工業和信息化部電子第五研究所,廣東廣州 510610)
在近場掃描電磁圖像的處理[1-3]中,需要對電磁圖像進行變換,如空域變換、頻域變換,近場掃描電磁圖像通過電磁場探頭探測得到[4-6]。傳統的快速傅里葉變換能夠對電磁圖像進行快速運算后得到結果,但基于近場掃描電磁圖像所反映的電磁輻射圖案的多樣性,希望能夠設計一種算法去學習這些圖案的特征,從而為電磁圖案的后續分析如聚類等提供有效的圖案特征,神經網絡是最適合學習圖案特征的框架,在研究的過程中發現神經網絡不僅可以有效地學習到電磁圖案的特征,還能夠學習到離散傅里葉矩陣。
目前,深度學習的絕大多數構建模塊、技術和架構都基于實數的運算和表征。但是,近來在循環神經網絡和其他更古老的基礎理論上的分析表明復數可以有更加豐富的表征能力,也可以促進對噪聲魯棒的記憶檢索機制[7-9]。盡管它們在帶來全新的神經架構上有引人注目的性質和潛力,但由于缺少設計這種模型所需的構建模塊,復數值的深度神經網絡一直處于邊緣化的狀態[10]。隨著計算機硬件的發展,神經網絡的應用越來越廣泛,在預測、分類方面取得了很大的應用[11],比如推薦系統、人臉識別等。
Reichert 等人從生物學的角度出發,將復數神經元用在深度神經網絡中,這些使用復數表示的神經元具有更加豐富的表達能力,復數值的公式允許人們用神經元的放電率和活動的相對時間來表示神經元的輸出。該復數神經元的振幅代表放電率,而其相位則代表活動的相對時間[12]。復數中的相位信息在信號處理時也是十分重要的,在語音信號中,相位信息影響著語音信號的可理解性[8]。Oppenheim 和Lim 還表明,在圖像的相位中存在的信息量足以恢復以其大小編碼的大部分信息。事實上,相位在編碼形狀、邊緣和方向時提供了對象的詳細描述[13]。
最近,Rippel等人將傅里葉譜表示用于卷積神經網絡,提供一種在頻譜域中參數化卷積核權值的技術,并在信號的頻譜表示上執行池化[14],然而,作者在論文中回避了執行復數值卷積,而是從空間域中的實值進行核卷積構建。為了確保譜域中的復數值參數化映射到實數值核函數,作者對譜域權重施加了共軛對稱約束,這樣當對它們應用傅里葉逆變換時,它只產生實數值的核函數[14]。
離散傅里葉變換作為一種有效的信號處理工具得到了廣泛的應用,經典的快速傅里葉變換[15]更是將這個算法的應用發揮到了極致,但是快速傅里葉變換涉及到復數運算,而目前神經網絡在復數運算方面基本上是不支持的,為了將神經網絡應用到信號處理中,一方面設計可以進行復數運算的神經網絡,另一方面是通過某種變換和設計,將復數進行拆解,使之能夠按照實數進行計算,卻不丟失原來復數運算包含的信息。
該文研究的離散傅里葉矩陣構建方法,完美地避開了復數運算,同時保留了和原始矩陣同樣的信息量,并基于神經網絡來學習和重構離散傅里葉矩陣,該矩陣可用于近場掃描之后的數據處理中[17]。
1 研究內容
1.1 離散傅里葉矩陣設計的數學原理
對于一個長度為N的信號序列x=[x0,x1,…,xN-1],它的離散傅里葉變換公式為:
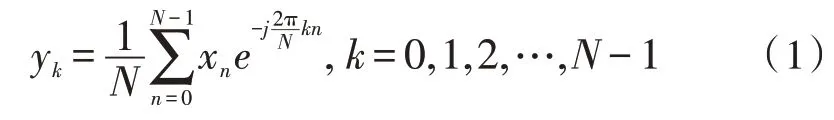
式(1)可以寫成點積的形式:

式(2)寫成矩陣形式:

式(3)寫成矩陣形式:

其中,F∈RN×N,(F)kn=。式(2)、(3)都包含復數,復數運算是比較復雜和耗時的,因此引入歐拉公式:
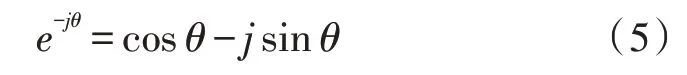
對此,令:

代入式(5)可得:
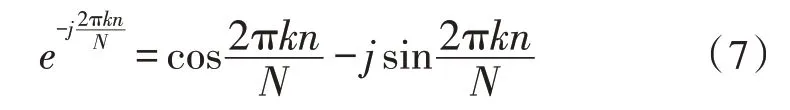
將式(7)的實部和虛部分開,然后排放在一個矩陣的上半部分和下半部分:

令WFourier表示式(8)右邊的復指數值構成的矩陣,x表示[x0,x1,…,xN-1]T,則式(8)可以簡寫為:

y和包含的信息是完全一樣的,但是式(9)不包含復數計算,因為引入歐拉公式將其實部和虛部放在矩陣的上半部分和下半部分,所以的長度是y長度的2倍。
1.2 神經網絡設計
1.2.1 神經網絡架構
如圖1 所示,所設計的神經網絡共有兩層,輸入層因為用于原始數據輸入,通常只是進行了展平處理,對數據沒有影響,所以不作為層計數,隱藏層的神經元數量為輸入層神經元數量的2 倍,輸出層只有一個神經元,用于計算損失。
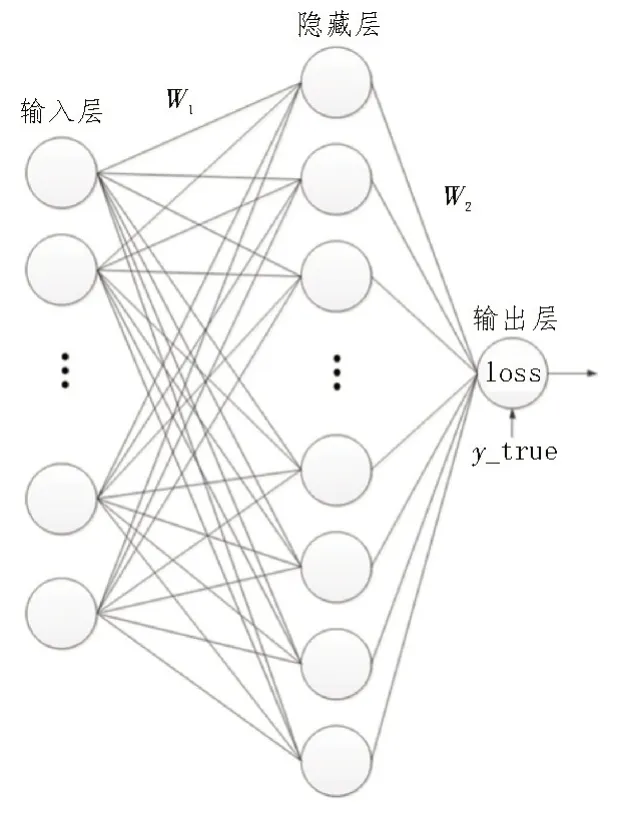
圖1 神經網絡結構設計
1.2.2 訓練過程
如圖2 所示是神經網絡重構離散傅里葉矩陣的原理框圖,重構步驟如下:
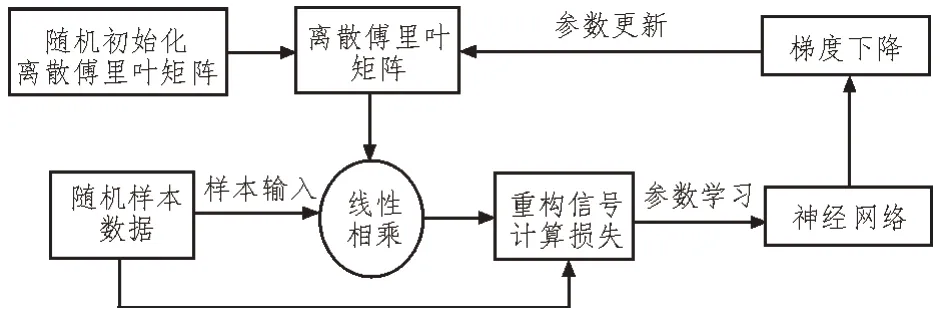
圖2 神經網絡訓練的原理框圖
1)隨機初始化離散傅里葉矩陣WFourier,該矩陣是神經網絡需要學習的參數;
2)生成隨機樣本輸入x,與第1)步的參數矩陣進行線性相乘;
3)根據式(3)取出對應的實部和虛部,進行信號的重構,重構的方法如下:
已知一個信號的離散傅里葉變換的系數y=a+jb,其中y是一個復數,根據傅里葉分析理論,則對應的信號部分x為:

代入y=a+jb,展開可得:
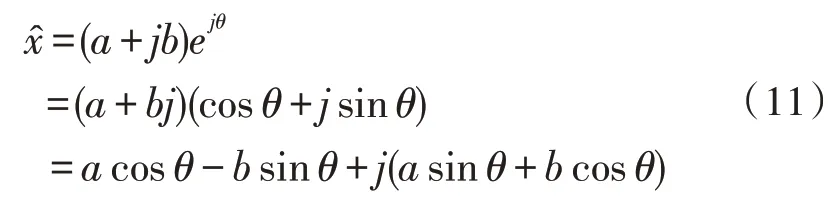
其中,a和b對應第3)步中實部和虛部。
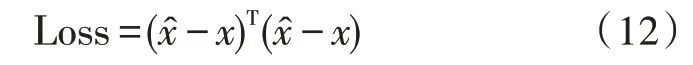
5)式(12)的損失函數(LossFunction)作為神經網絡訓練精度的衡量標準,并計算它的梯度后,進行參數更新,重復從第(1)步-第(4)步繼續訓練,直到訓練達到指定的次數或者符合誤差要求。
2 實驗結果與分析
文中的實驗環境為搭載Intel(R) Core(TM) i5-8265U CPU@1.60 GHz 1.80,雙核1.60 GHz 主頻處理器,內存8 GB的計算機,實驗在64位Windows 10操作系統,使用神經網絡框架pytorch 1.8.1+cpu 版及numpy1.16.5 條件下進行實現。
如圖3 所示是理論計算的離散傅里葉矩陣與神經網絡學習到的離散傅里葉矩陣的對比,其中神經網絡迭代次數為10 000次,從圖形上可以直觀地看出,神經網絡基本上學習到了離散傅里葉矩陣的特征。
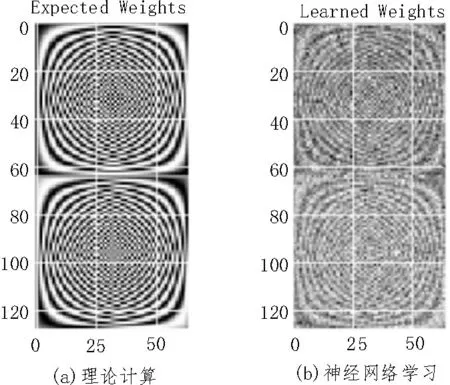
圖3 兩種方法得到的離散傅里葉矩陣的對比
如圖4和圖5所示,可以看出重構信號的損失值和RMSE在2 000次迭代以后基本上不變,即通過神經網絡學習到的離散傅里葉矩陣已經能夠很好地還原原始信號,同時也說明在精度上,神經網絡學習到的離散傅里葉矩陣基本上不再隨著迭代次數的增加而有所提升。

圖4 重構信號的損失值隨迭代的變化
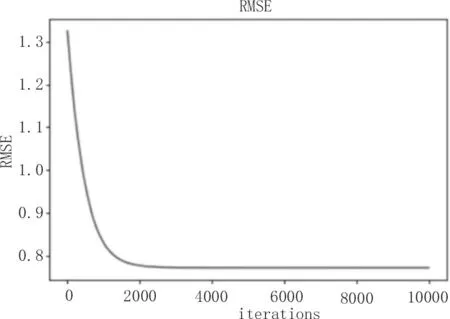
圖5 離散傅里葉矩陣均方差隨迭代的變化
圖6 是原始的信號,圖7 是使用神經網絡學習的離散傅里葉矩陣重構的信號,可以看出,兩種信號幾乎完全相同,這是因為在神經網絡訓練2 000 次之后,神經網絡學習到的離散傅里葉矩陣基本上與理論計算的離散傅里葉矩陣完全相同,這可以從圖4和圖5 得到驗證。文中的實驗數據沒有加入噪聲,因而重構信號的誤差取決于神經網絡學習到離散傅里葉矩陣的誤差,從圖5 中可以看出,這個誤差在迭代2 000 次之后基本上再無變化,假如數據包含噪聲,那么這種情況可能是神經網絡在訓練時過擬合了,因為從圖3 來看神經網絡學習到的離散傅里葉矩陣和理論計算的離散傅里葉矩陣是有差別的,而迭代次數在2 000 次之后對這種差別卻無明顯的改善,說明神經網絡在結構分布上可以完美地學習到離散傅里葉矩陣,但是在數值精度上不能完美地接近。通過實驗得到迭代次數與模型損失關系如表1 所示。
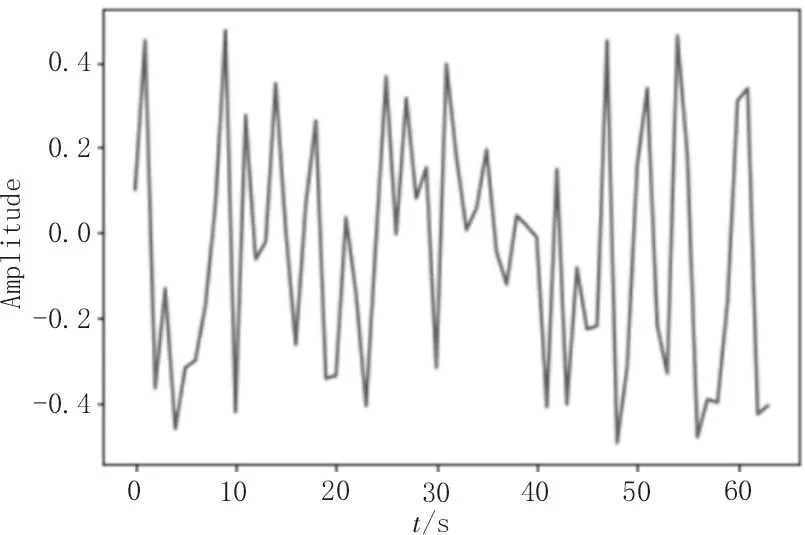
圖6 原始信號
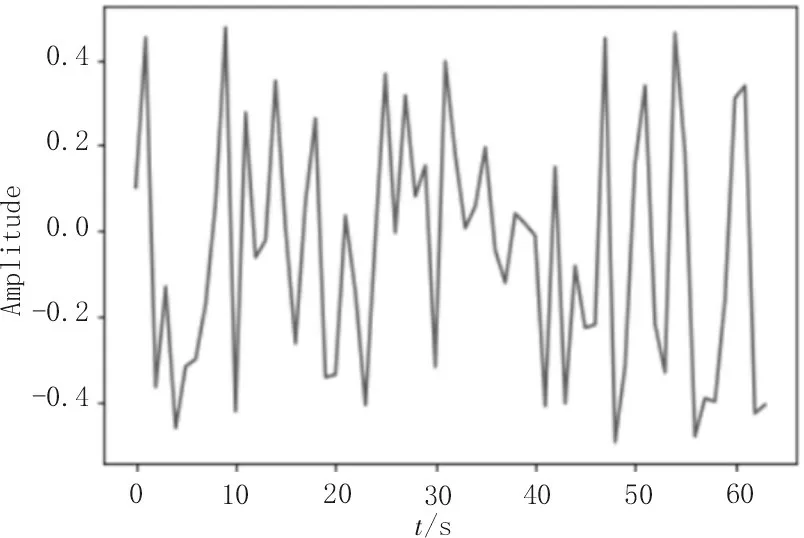
圖7 神經網絡學習的離散傅里葉矩陣重構的信號
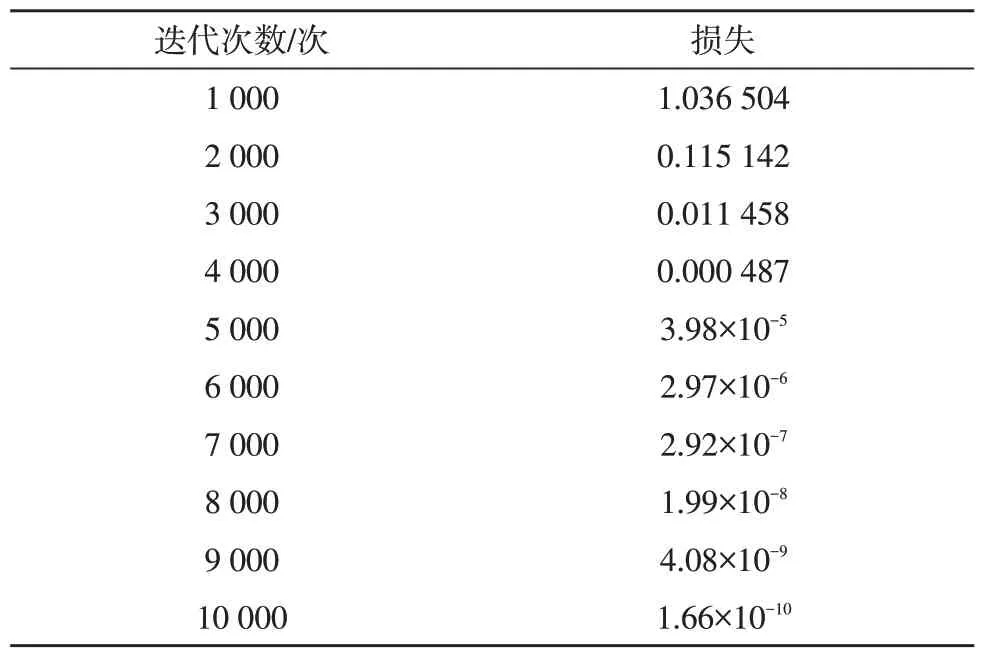
表1 迭代次數與模型損失
通過表1可以看出,迭代次數在4 000 次以后,損失值基本上接近于0。
3 結論
該文提出了一種將離散傅里葉變換避開矩陣運算的復數操作方法,并使用神經網絡來學習該矩陣。可以看出神經網絡很完美地學習到了該矩陣,且用該矩陣重構的信號與原始信號基本相似。其根本原因是該文設計的神經網絡是一種線性變換,而離散傅里葉變換也是一種線性變換。那么在使用隨機梯度下降的迭代中,只要迭代次數足夠,就可以完美地學習這種線性變換。后續可研究的工作是用神經網絡研究二維離散傅里葉變換,同時結合圖像降噪的理論研究近場掃描電磁數據的降噪設計。

