基于慣性傳感器行人室內定位導航算法研究

劉昶

(合肥市測繪設計研究院，安徽 合肥 230000)

1 引 言

目前發展比較完善的全球定位系統(GPS)技術，在一些易受遮擋、GPS信號干擾、室內場合等環境下無法提供有效的定位服務，而基于微機電系統(micro-electro-mechanic system，MEMS)的慣性傳感器的定位技術能很好解決這一問題，慣性系統是一種自主導航系統，它能夠提供連續性好、短期精度高和穩定的導航信息(如位置、航向、姿態角數據)[1]。隨著慣性傳感器不斷在人們生活中得到應用和發展，特別在室內的環境中，如通過加速度檢測行人的步長和步幅，結合慣性傳感器提供的航向信息，通過航位推算確定行人位置(pedestrian Dead Reckoning，PDR)[2～4]。Robertson等提出基于鞋底安裝慣性傳感器的貝葉斯定位算法框架，采用卡爾曼濾波估計行人位置[5]；John-OlofNilssion等提出了基于鞋綁式零速度修正(Zero Velocity Update，ZUPT)輔助的慣性導航系統，提供開源的代碼，但算法參數設置繁多，對不同的環境定位應用帶來不便[6]；Skog I，H?ndel P等研究ZUPTs在輔助慣性導航系統中局限性和傳感器誤差建模影響分析[7]。

本文以航向姿態參考系統(AHRS)為基礎，IMU(Inertial Measurement Unit)的三軸陀螺儀和三軸加速度計追蹤載體運動的旋轉和平移，提出對三軸動態方向估計濾波融合修正，優化設計行人行走中零速度檢測算法，通過對行人靜止判斷，進行加速度方向校準和行人速度漂移誤差的剔除，最后對時刻速度積分獲取精確的位置信息，從而提高系統定位的精度。

2 行人步態跟蹤定位算法結構

當前MEMS IMU的應用精度相對較低，進行獨立的慣性導航解算時，其解算的位置積累誤差隨著時間成三次方發散，從而失去慣性傳感器導航定位的現實意義，因此采用零速修正(ZUPT)可有效解決慣性傳感器的積累誤差的三次方發散問題。行人行走過程如圖1所示： 從運動可以看出， 行人行走的明顯規律為“運動—靜止—運動—靜止……”的過程，腳底A與地面接觸時會有短暫的靜止時間，從時刻T=0.48 s到T=0.72 s的行人短暫△T時間段內為靜止狀態，此時行人速度VA=0，針對△T靜止時間段內進行零速度修正，其修正效果如圖2(a)，其中慣性導航系統(INS)是未經零速度修正的速度誤差呈三次方發散。INS+ZUPT為經過零速度修正后誤差發散情況，由此可得，經過零速度修正后的速度獲取的位置信息，如圖2(b)所示，位置誤差與行人步數成一定的線性相關。

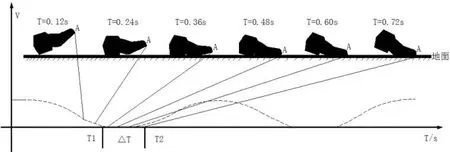
圖1 行走動態階段

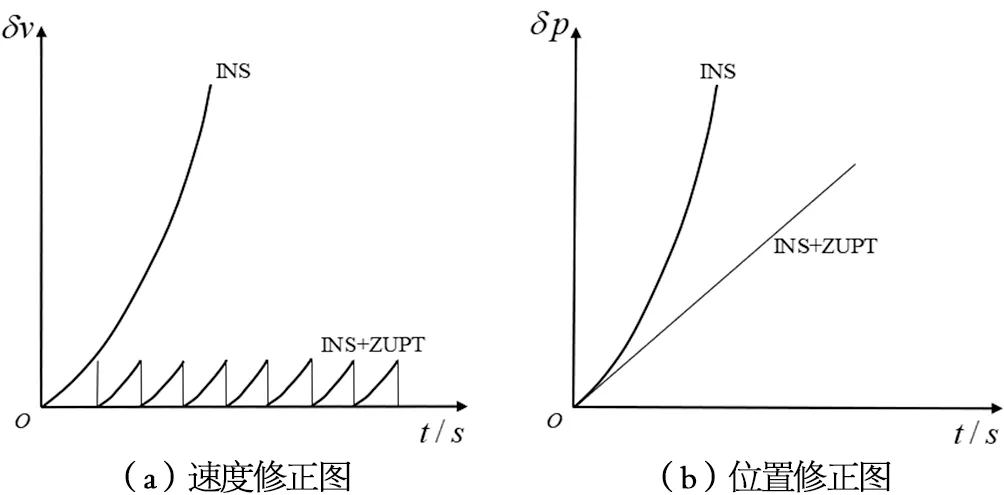
圖2 零速修正結果

本文將MEMS慣性傳感組件安裝于人體足部，結合人體足部行走特征，通過互補濾波融合的方向估計修正算法，及足部零速檢測判斷，構成基于方向和零速修正的慣性輔助行人跟蹤定位系統。該系統主要為三部分組成：

①航向姿態更新算法。方向估計更新在AHRS系統上，采用方向四元數(Quaternion)算法解算，通過MEMS慣性傳感器的三軸加速度計和三軸陀螺儀的互補濾波融合對載體的三軸姿態進行精確方向估計。與歐拉角算法相比，避免采用三角函數運算，既保證更新速率，計算時也不會出現奇異性

②零速度檢測算法。零速度檢測算法通過MEMS慣性傳感器的三軸加速度值檢測行人行走過程中足部與地面接觸時間段內的零速度，本次實驗設計廣義似然比檢測算法(GLRT)，通過設置零速檢測閾值判斷是否處于零速度狀態，為零速更新提供必要條件。對于正常行走步態可實現很好的檢測，但對于跳動、抖動的步態難以檢測，目前本文只研究正常行走步態。

③修正算法。修正算法主要是削弱圖2(a)和圖2(b)中的速度積累誤差和位置積累誤差的發散問題，通過對方向修正及零速、非零速時漂移誤差的剔除更新，獲取用于導航計算最終人體速度。

3 濾波融合方向估計算法

AHRS系統，是一種主要采用慣性傳感器數據測量空間姿態的傳感系統，一般情況，AHRS系統能夠確定載體的三軸姿態[10]。

方向是基于AHRS系統進行估計，采用慣性傳感器的三軸加速度計和三軸陀螺儀，分別量測載體坐標系下三軸上的加速度和角速率，利用陀螺儀補償角解算出量測誤差的四元數的微分形式，從而估計出地理坐標下的方向四元數。

設三軸陀螺儀在載體坐標系下的角速度為wx，wy，wz，則角速度向量Ww：

Ww=[0wxwywz]

(1)

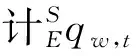
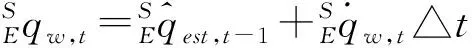
(2)

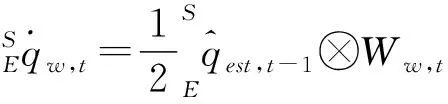
(3)

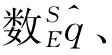
(4)

(5)

則設誤差函數f：

(6)

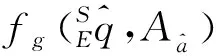
通過迭代計算來估計方向四元數，即計算公式為：

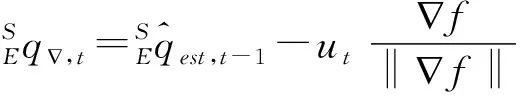
(7)

(8)

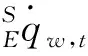
4 零速度檢測算法

零速檢測的目的是檢測行走過程中速度為零的時段，即對圖1中△T的時間段內VA=0的檢測，零速度檢測是觸發零速修正的前提，也是實現速度誤差清零關鍵步驟。崔瀟等文獻采用一種多條件閾值復合檢測算法(比力模值、比力方差、角速度模值)，只有三條件同時滿足，對零速檢測效果表現出更有效性[8]；Skog I，H?ndel P，Nilsson J O等通過與常用的加速度方差檢測、加速度幅度值檢測、角速度能量檢測方法相比較，它們都存在一定缺陷，而廣義似然比檢測方法適用性更有效[9]。

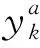
(1)加速度值和角速度值向量表示。

(9)

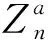
(2)檢測算法公式。

(10)

式(10)中g為重力加速度值。

(3)設置檢測閾值γ：

(11)

當式(11)滿足條件，認為速度為零(足部靜止狀態)，設置為1，非零速度設置為0(足部離開地面)。

對本文樓道采集的數據進行零速檢測，截取部分時段數據如圖3所示，Stationary為零速檢測折線圖，數值為1表示為行人靜止狀態，由Stationary折線圖可得，零速檢測對行走過程中靜止時刻能有效檢測。X、Y、Z分別為三軸加速度，X、Y軸加速度周期性的出現加速度為零(aA=0)，即對應行人速度為零的時刻(vA=0)。

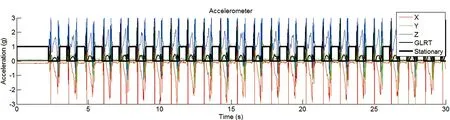
圖3 零速檢測結果

5 基于方向和零速修正輔助定位算法

本章節修正算法包括對方向估計后三軸方向的修正以及零速檢測后的速度修正，并對非零速狀態下的速度漂移改正，來約束行人在運動過程中的方向漂移以及速度漂移，從而提高行人行走狀態下的位置更新精度。

5.1 互補濾波融合方向修正算法

(12)

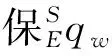
(13)

(14)

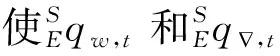
(15)

則式(14)中可簡化為：

(16)

將式(2)、式(15)和式(16)帶入式(12)，可簡化為：

(17)

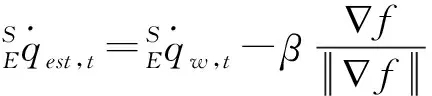
(18)

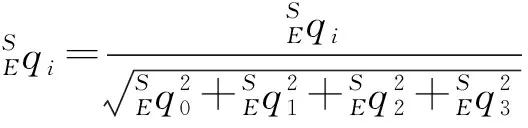
(19)

5.2 零速及速度漂移修正輔助定位

將MEMS慣性傳感器固定在行人足部，按照文中5.1節的互補濾波融合算法的方向修正和第4節的零速檢測的零速更新修正實現行人行走狀態下導航定位。

①計算平移加速度。通過5.1節的方向四元數估計，將加速度計量測的三軸加速度通過旋轉變換到地理坐標系下，得到精確地理坐標系下的三軸加速度a。即：

(20)

式中?表示將三軸加速度通過四元數乘積的旋轉變換計算。

②計算平移速度，將①中轉換得到的地理坐標系中實際三軸加速度a，通過對a數值積分獲得速度v。

vt=vt-1+at△t

(21)

式(21)中，△t為采樣周期。在對通過積分求取的速度，并通過零速更新修正，當判斷在某時刻速度為零時，速度設置為零，并觸發ZUPT更新機制，實現行人軌跡定位，同時本文考慮對非零時刻的速度，剔除非零速存在的整體漂移vD。

v=v-vD

(22)

③計算行人位置。對最終求得的速度v進行積分獲取行人位置P。

Pt=Pt+vt△t

(23)

5.3 室內導航定位算法流程

基于以上算法結構，設計基于慣性傳感器的行人室內導航定位算法系統的完整結構圖，如圖4所示。

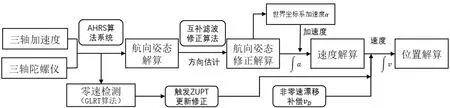
圖4 行人定位導航算法工作原理流程圖

6 實驗結果及驗證

為了驗證設計的行人步態導航定位系統的有效性，本次實驗區為連續的矩形樓道走廊，其實驗區示意圖如圖5所示，慣性傳感器為X-IMU型號，固定于足部，如圖6所示。實驗為閉合路徑，共四次拐彎，起點為西北處，沿樓道連續行走兩圈，數據量共166.04×2 m。

圖5 樓道示意圖 圖6 慣性傳感器與足部固定位置示意

利用MATLAB軟件編寫上述算法，實現INS(未修正)、INS+ZUPT(修正，包括方向和速度修正)與實際樓道路徑對比實驗的方法。圖7為實驗行走路徑對比結果。

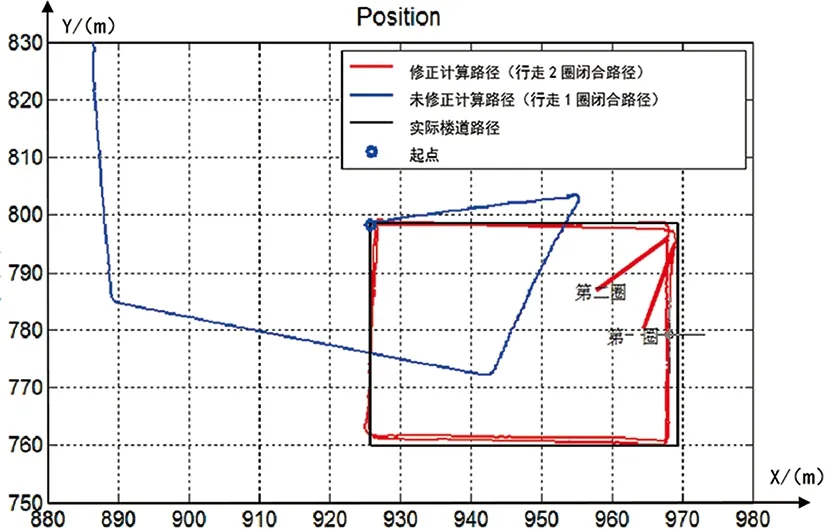
圖7 兩圈矩形軌跡定位結果

表1為在矩形樓道中連續行走兩圈，回到最初起點的路徑統計結果，第一圈為各拐彎路徑的行走結果，然后統計第一圈和第二圈的統計結果。

表1 行走距離結果

在圖7中得：在實驗中，藍色路徑為行走一圈路徑，隨時間推移已嚴重偏離實際路徑，且位置誤差積累不斷增大，主要原因是未經方向誤差補償修正和速度修正導致。則紅色路徑是采用互補濾波融合方向修正計算，能有效補償陀螺儀的漂移誤差和濾除加速度計的高頻錯誤，從而獲取精確的方向，并結合零速修正，解決速度誤差積累，且與實際路徑相吻合，有效實現行人步態導航定位。在實驗中，兩圈矩形路徑行走的最后閉合差約為 1.6 m，其定位精度均在1.1%以內。

7 結 語

基于MEMS的慣性傳感器行人步態室內導航定位算法的實現，主要采用基于AHRS系統的互補濾波融合方向估計算法和零速修正技術完成行人跟蹤定位的過程，本文重點論述了在AHRS系統上，融合MEMS慣性傳感器的加速度計和陀螺儀的數據提出一種濾波融合方向估計算法，有效補償陀螺儀漂移，并有效的計算出全局方向估計，結合足部慣性傳感器的加速度和角速度特性設計零速檢測算法(GLRT)，并觸發ZUPT更新，完成跟蹤定位。在對缺少GPS信號的室內和室外環境均可有效的較長時間進行跟蹤定位，具有重要的意義。