多機動控位水雷隊形控制技術

蔣 平，李加強

（1. 中國船舶集團有限公司第七一〇研究所，湖北 宜昌 443003；2. 清江創新中心，湖北 武漢 430076）

0 引言

機動控位水雷本質上是一種大型 AUV。與AUV集群相似，機動控位水雷編隊協作執行任務的能力相較于單個機動控位水雷執行任務具有顯著提升。通過各水雷之間的協調與合作，不僅可以改善單個水雷的基本能力，而且在各水雷的交互中進一步體現了社會行為。通過共享資源（信息、知識、物理裝置等）擴大完成任務的能力范圍，如分組形成編隊能夠提高系統的探測能力、導航能力和通信范圍等。通過設伏、圍捕、齊射、梯隊攻擊等方式來提高任務的執行效率，并大大提高了水雷行為的智能化程度。

在水下隱蔽作戰中，機動控位水雷可突破傳統水雷位置固定、封鎖范圍有限的限制，可以通過集群編隊式移動，更為有效地執行區域覆蓋式目標搜索、協同探測、攻擊等任務，共同完成傳統水雷無法完成的復雜任務。要實現多機動控位水雷編隊協作，隊形控制是首先要解決的技術難題。近年來，隊形控制已經在無人機、無人船、移動機器人等領域得到了一定應用，水中兵器領域相關高校[1-2]和院所[3-4]在水下領域也開展了相關研究，取得了一些研究成果。從已有的文獻來看，常用的隊形控制方法主要有：領航–跟隨者方法、虛擬結構方法、行為融合方法、基于強化學習的方法等，并在此基礎上衍生出許多改進和組合方法。

1 領航–跟隨者法

領航跟隨者方法也被稱為主從式編隊方法：編隊中設置1臺AUV作為領航者，領航者按照預定的航路規劃航行；編隊中其他AUV則作為跟隨者，與領航者保持一定的距離，使整體呈現相對固定的隊形航行。領航跟隨者編隊方法簡單明了，沒有太多復雜理論和計算，跟隨者只需要通過觀測領航者的運動信息來調整自身運動軌跡，是目前應用最為廣泛的編隊方法。

機動控位水雷配備了磁羅盤、DVL、GPS/北斗等設備用來進行導航定位解算，是一種具備自主航行能力的新型水雷。機動控位水雷在進行水下組網通信和區域封鎖/巡航時，需要通過保持隊形來得到更好的效果。由于機動控位水雷本身具備獨立的導航能力，因此可讓每一條水雷按預先設置的航路行進（每條航路之間保持固定的間距），再通過水聲通信交互位置信息，以位置、速度等信息作為隊形控制的對象，通過領航–跟隨者方法來實現隊形控制的工程應用。

對不同面積區域的覆蓋封鎖，機動控位水雷群的數量也是不定的。為了簡化模型并能將多 AUV的隊形控制方法移植到水雷上，本文選取3條機動控位水雷進行編隊，包括1條領航者水雷和2條跟隨者水雷。

2 機動控位水雷模型

機動控位水雷從流體結構和動力特性上來分析，是一種典型的欠驅動 AUV，其水平面運動動力學和運動學方程[5]：

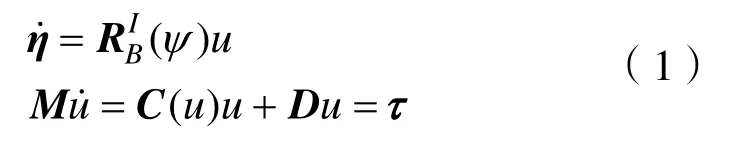
式中：η=[xyψ]T，其中[xy]T表示機動控位水雷在水平面上的位置信息；ψ為偏航角；u=[μvr]T表示載體坐標系下水雷的前向速度、側向速度及偏航角速度。

雷體坐標系到大地坐標系的轉換矩陣：

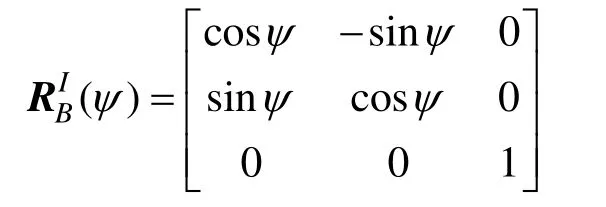
科里奧利–向心矩陣：

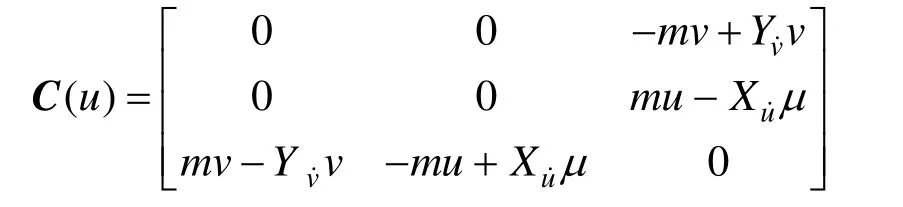
慣性矩陣：

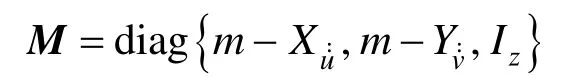
水動力阻尼矩陣：

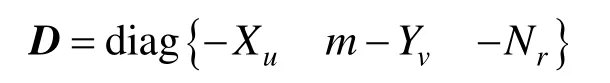
機動控位水雷軸向力、側向力及偏航力矩的外部控制輸入：

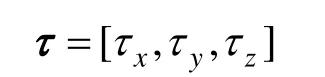
對于機動控位水雷來說，幾乎不受側向力，即τy=0。

3 基于位置信息的領航–跟隨者法

傳統的多 AUV在進行領航–跟隨編隊時，領航者按照事先設定的航路規劃航行，跟隨者則通過水聲通信廣播的方式獲取領航者的位置和速度信息，自主調整自身的航行路線和速度來保持隊形。與常規AUV不同的是，機動控位水雷有2個特點：1）作為水雷，隱蔽性是其重要特征，因此無法頻繁的通過水聲通信來進行位置信息交互，并且由于相互之間的距離較遠，水聲通信數據傳輸量有限，因此需要盡可能的減少交互信息；2）編隊中的每一條機動控位水雷，都具備出色的導航定位的能力，且相互間距離足夠遠，因此編隊航行時可不考慮航向偏差和相互規避。

對于對領航者狀態信息需求較少的隊形控制方法，文獻[6]和文獻[7]中提出了一種僅需要領航者的位置及航向的隊形控制器，而文獻[8]設計的控制器只利用了領航者的速度信息。本文結合機動控位水雷的自身特點和應用場景，設計了一種只需要領航者的位置信息的控制方法。

3條機動控位水雷組成的編隊如圖1所示，為簡化流程，假設：1）3條水雷航行時位于同一深度，這樣就將機動控位水雷的運動由3維簡化到水平面的 2維平面上；2）3條水雷均按設定航路進行直航，分別處于互相平行且等間距的航線上，這樣可以更容易地保持隊形。

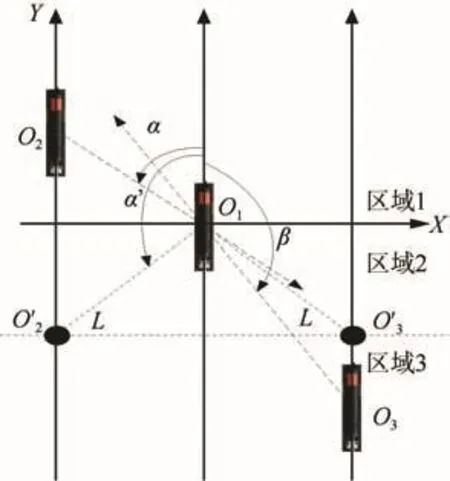
圖1 領航者與跟隨者所處位置示意圖Fig. 1 A sketch of the positions of the leader and follower

圖中O1(x1,y1)是領航者的位置，O2(x2,y2)，O3(x3,y3)分別是2個跟隨者的位置，整個編隊期望保持的隊形是以O'2O1O'3為定點的三角形，其中O'2(x'2,y'2)，O'3(x'3,y'3)是跟隨者在編隊中的期望位置。

以伴隨者O2的隊形控制方法進行分析，α為O1O2'和直航方向的夾角，α'為O1O2'和直航方向的夾角，伴隨者O2在獲知了領航者O1的位置信息后，通過計算：

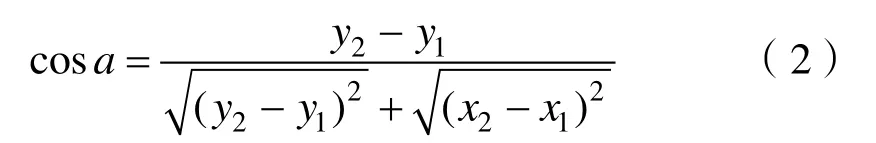
得出當前O2當前的位置分布，包含2種情況：

由圖1可見，伴隨者O2的期望位置O2'位于區域2，有：

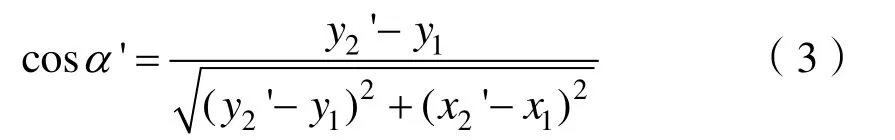
當伴隨者O2位于區域1時，定義該狀態為N1，狀態判據為

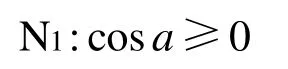
當伴隨者O2位于區域 2時，此時又包括2種狀態，分別定義為N2，N3，狀態判據為

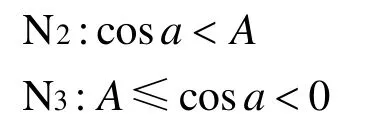
3種狀態與對應的控制策略見表1。

表1 跟隨者狀態與控制策略Table 1 State and control policy of the follower

4 模糊PID控制器

按照表1的控制策略，處于跟隨狀態的機動控位水雷，可通過調節自身的航行速度保持隊形，采用模糊PID控制方法設計速度控制器：

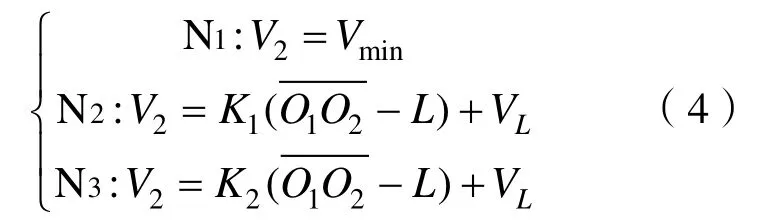
式中：V2為跟隨者當前的速度；Vmin是機動控位水雷最小航行速度；VL是整個編隊的期望速度；L為三角編隊時領航者與伴隨者之間的直線距離期望值；系數K1,K2＞0

如上所述，當編隊處于狀態 N1時，跟隨者位于領航者前方，此時只需要保持最低航速，直到進入狀態N2；在N2狀態下，此時跟隨者位于領航者和跟隨期望位置之間，只需選取合適的位置比例控制參數K1即可使編隊趨于期望隊形；當跟隨者位于狀態3時，情況較為復雜，為了確保不丟失跟隨目標和快速調整隊形，不僅需要基于跟隨者與領航者之間的距離為反饋，根據距離的大小，設置多級調控模式，因此 N3狀態下隊形控制的關鍵在于速度控制器的控制參數K2。

對于控制參數K2，本文采用模糊推理的方式來獲得，設計單變量二維模糊控制器輸入選取D和V，其中D=y2'-y2，表示跟隨者的期望位置與當前位置在Y軸上的差值，V表示跟隨者的當前速度。

圖2 模糊控制器框圖Fig. 2 Fuzzy controller block diagram

模糊輸入D的論域Y= [ 0,+ ∞]，對應的模糊子集為Ai(i=1,2,3,4)，對應的模糊語言為{近、較近、較遠、遠}，取梯形隸屬函數，其中D1為領航者與跟隨者在Y向上的最大允許間距。

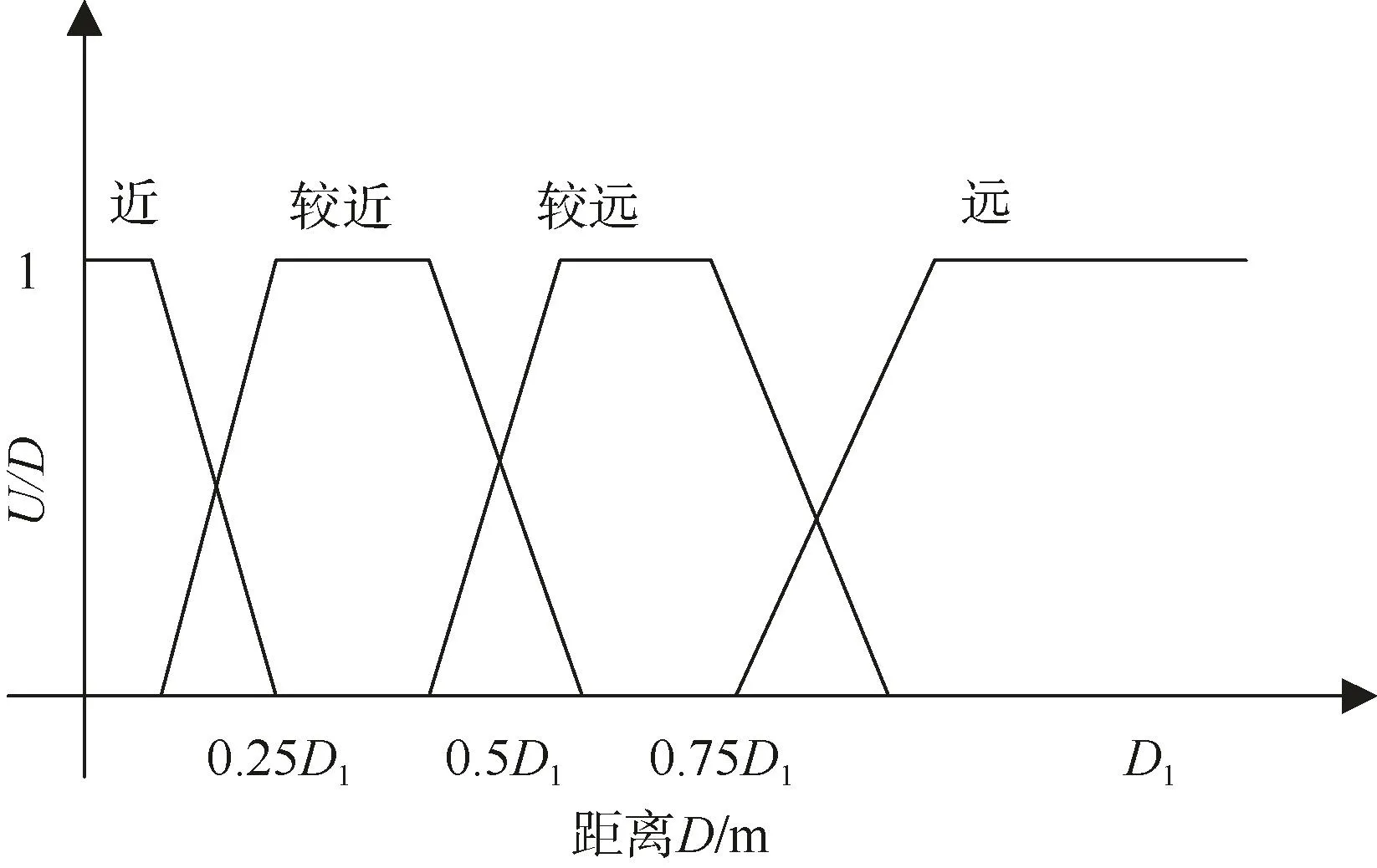
圖3 跟隨者Y向位置偏差隸屬函數Fig. 3 Y-direction position deviaton membership function of the follower

模糊輸入V的論域Y=[VminVmax]對應的模糊子集為Bi(i=1,2,3,4)，對應的模糊語言為{慢、較慢、較快、快}，取梯形隸屬函數。

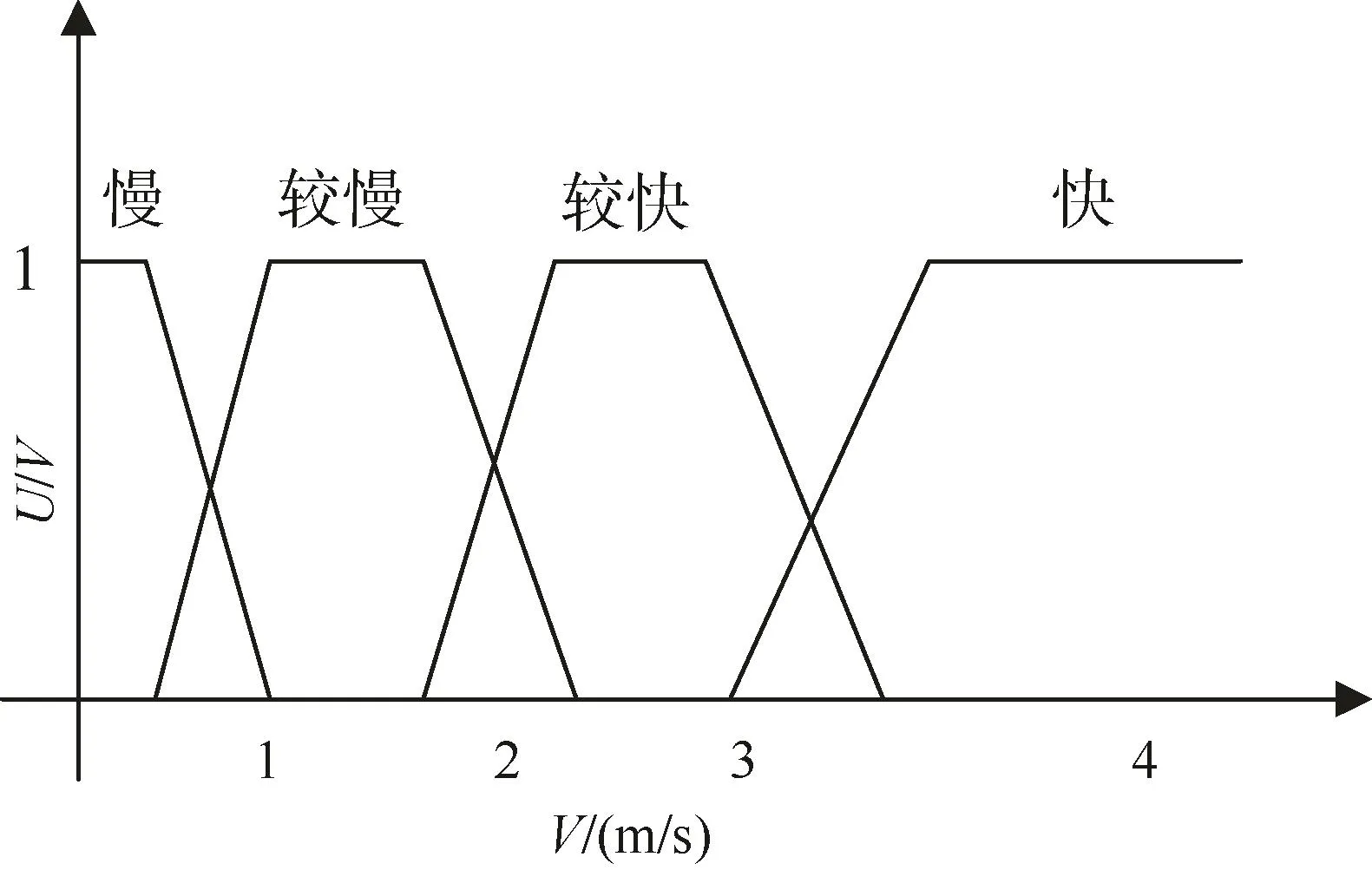
圖4 跟隨者速度隸屬函數Fig. 4 Velocity membership function of the follower

速度控制器的控制參數K2，論域Y= [ 0.01,0.1]，對應的模糊子集為zi(i=1,2,3,4,5)，對應的模糊語言為{小、較小、中、較大、大}，取梯形隸屬函數。

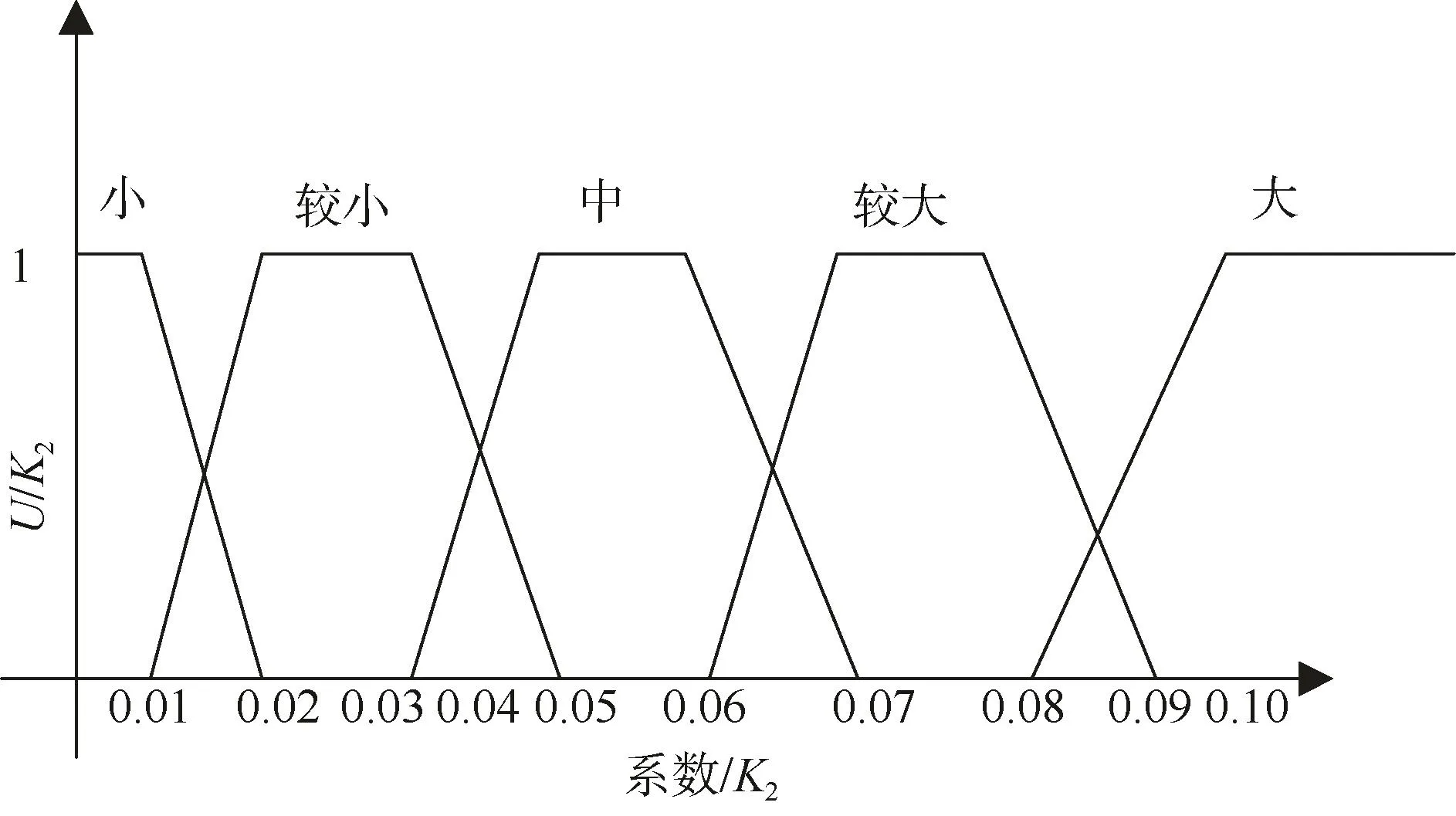
圖5 跟隨者控制參數隸屬函數Fig. 5 Control parameter membership function of the follower

根據上述分析，制定K2模糊推理規則如表 2所示。

表2 模糊推理規則表Table 2 Table of fuzzy inference rules

在得到上述推理后，需要對推理結果解模糊化從而得到最后輸出。解模糊化的方法有重心解模糊化法、面積和中心解模糊化法、最大隸屬度值解模糊化法等。本文采用最常用的重心解模糊化法。

由模糊規則AiandBi→k得到推理結果Cn'：

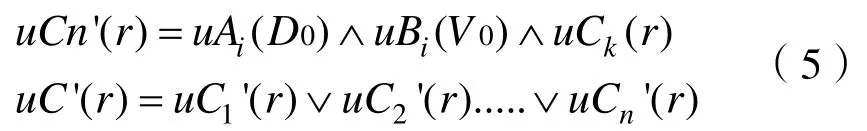
式中：∧表示最小值min；∨表示最大值max。

模糊集合C'隸屬函數的“重心”為

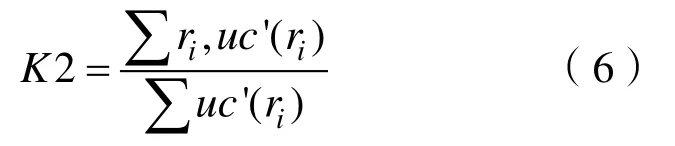
在得到整個輸出范圍內離散采樣點的重心值后，取K2模糊集合中最接近上述計算的值作為輸出。

5 仿真驗證

上述章節選取跟隨者O2作為研究對象，跟隨者O3與跟隨者O2中心對稱，控制方法與跟隨者O2相似。

在MATLAB上對本文的隊形控制方法進行仿真驗證，3條機動控位水雷的坐標點分別為跟隨者1（100，100）、領航者（0，0）、跟隨者 2（–100，–200）沿Y軸方向運動1 000 m，期望速度跟隨者VL=2 m/s，Vmin=1 m/s，Vmax=4 m/s，期望的距離L1=L2=200 m，通信周期10 s，最終呈現正三角隊形。采用上述PID模糊控制器，機動控位水雷群的運動軌跡和速度曲線如圖6–7所示。

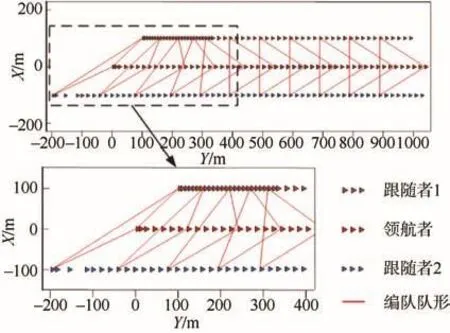
圖6 領航–跟隨者航行軌跡Fig. 6 Path of the leader-follower

由圖6可以看出，3條機動控位水雷開始航行時，跟隨者1和跟隨者2分別在期望位置的前方和后方，在模糊PID控制的作用下，逐漸構成了三角形隊形并趨于穩定。圖7的速度曲線中，領航者保持期望速度勻速航行，跟隨者則根據實際隨處位置與期望位置不斷調整航行速度，最終達到期望隊形并保持穩定。

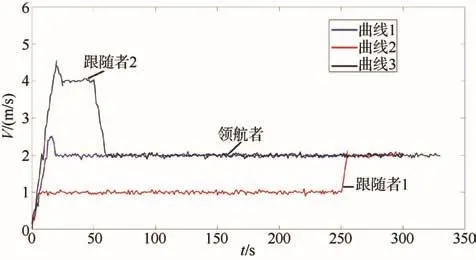
圖7 領航–跟隨者速度曲線Fig. 7 Speed curve of the leader-follower

6 結束語

本文基于水雷隱蔽、高效、可靠通信的應用場景，為盡可能減少水聲通信數據交互信息，提出了一種基于領航者位置信息的隊形控制方法，通過設計一種基于 PID模糊控制的跟隨者速度控制器。MATLAB仿真結果表明：該方法適用于機動控位水雷，能夠快速、穩定的形成隊形并穩定，具備工程應用前景。

本文的隊形控制方法，很大程度上依靠各編隊成員自身的導航精度，然而在真實水下環境中，多個機動控位水雷在長時間保持航向一致和間距穩定，對導航精度的要求非常高，對導航成本也是很大的考驗。下一步，將圍繞“高精度領航、低成本跟隨”的編隊構思，設計新的隊形控制方法，以適應機動控位水雷協同搜索、集群攻擊的任務需求。