無信號控制路段人車過道交互高效通行的數學模型分析

譚 俊，楊 光，李 衛，楊興愿

（湖南文理學院 土木建筑工程學院，湖南 常德 415000）

盡管有紅綠燈與人行橫道等眾多交通設施及標志來保障行人和車輛過道安全，但是由于非人行橫道區段占總道路長度比重大和部分人行橫道無交通信號控制等原因，導致行人在過道時人車沖突的事故頻發，其背后主要原因是行人和車輛駕駛員無法準確預測對方行為。

在無信號控制路段行人過道的行為主要取決于外部交通特征因素對行人過道決策選擇的影響以及行人本身對安全過道的心理狀態。為了解決人車交互通行的問題，已有大量學者進行了相關研究：王穎志、袁振洲等人采用人車交互事故的數據采集，從人車交互實況站在事故的視角上進行人車交互數據分類分析；連靜等人在大數據的基礎上建立模型，對人車交互的影響因素分析；楊城城等人針對人行橫道區段人車交互展開分析，提出提高通行率的建議。

無信號控制路段在國內城市支線道路大量存在，雖然方便了行人過道，但人車交互通行的沖突事故頻發，已引起交通管理部門的重視。文章通過對行人及車輛在直線區段建立數學模型進行仿真模擬分析，從而探索出不同情形下行人與車輛交互通行的最優過道方式，以達到安全高效通行的目的。

1 基本假定及參數取值

假定單輛車輛在直行車道不減速避讓行人條件下交互通行，車輛和行人軌跡近似為直線運動，人車不產生沖突，為了模擬方便，車輛模型簡化為矩形，道路行人模型抽象成單質點。通過調查顯示在車輛行駛頻繁的道路上，大多數行人選擇在車輛到來前的4~6 s的間隙過街，因此對行人與車輛距離在4~6 s時間與行車速度范圍內分類討論，這樣就能盡可能多覆蓋道路上人車交互通行的各種情況。

在車輛與行人的相對位置建立數學關系，人車相對位置由人車在坐標系的縱向距離D和橫向距離d共同確定，行人沿角度c進行過道。考慮人車之間不同的距離，再根據行人行走速度vr和車輛行駛速度vi，分不同工況進行數據模擬。根據文獻和大量現實數據的調研，選取行人的過道速度為5 km/h，對應的vr=1.2 m/s，車輛速度分別取值為10 km/h、30 km/h、50 km/h，對應的v1=2.7 m/s、v2=8.3 m/s、v3=13.8 m/s。模型中道路寬度、家用小車的尺寸等參數取值見表1。

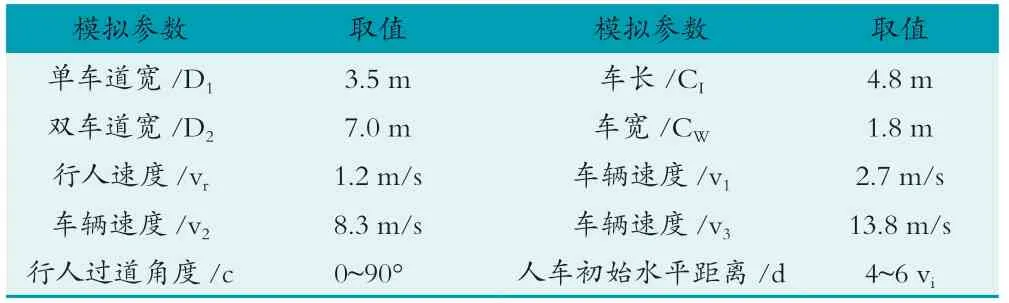
表1 模型參數取值表

2 人車交互通行軌跡數學模型建立

根據道路寬度、車輛尺寸、車輛速度、行人行走速度和人車相對位置等建立直角坐標系模型，通過構建數學方程表征人車隨時間的相對變化關系，從而模擬確定人車運動軌跡。

模型中車輛在與行人在互不干擾下各自做勻速直線運動，建立模型時，考慮行人沿一定的過道角度c通行，人車交互通行安全過道存在3種情況：①當車輛速度較快、行人速度較慢而人車初始水平距離相對較近時，此時車輛能夠在行人未過道之前駛離；②當車輛速較慢、行人速度較快而人車初始水平距離相對較遠時，此時車輛還未能逼近行人而行人已經實現安全過道；③在車輛速度、行人速度、人車初始水平距離3個不定因素影響下，導致行人通行與車輛駛離存在碰撞風險。在前2種情況下，行人過道與車輛駛離不相沖突，不存在發現碰撞，行人只需要直線通行即可。車輛速度、行人速度、人車初始水平距離均會對通行方式造成影響，因此可以嘗試通過固定車輛速度和行人速度去尋找造成不同通行結果的人車初始水平距離。模型示意圖，如圖1所示。

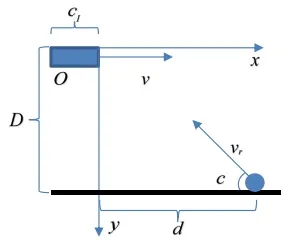
圖1 人車交互通行運動模型

模型中車輛與行人均為勻速直線行駛，對于行人在模型的行動軌跡為：

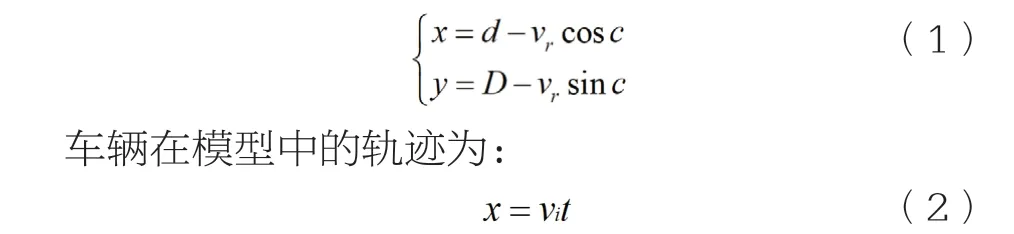
在行人決策選擇過道行動后，行人和車輛同時運動，行人安全通過車道和人車水平方向相遇分別對應一個具體時間，若前者小于后者，則說明人車交互通行是安全的，安全時刻的位置狀態用數學關系式進行描述為：

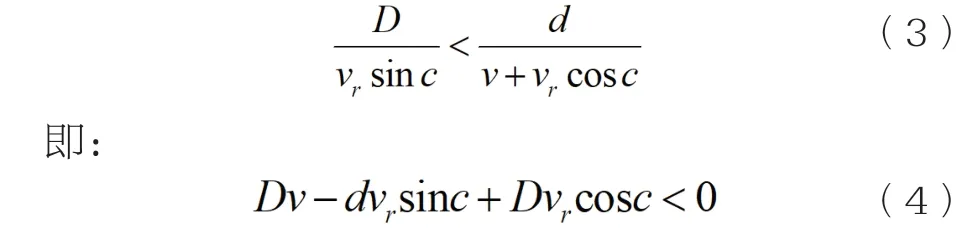
通過對模型參數的排列組合模擬各組工況下人車交互通行軌跡，其中調整行人的過道角度最為具有可行性，即，通過式（4）得到行人過道角度c的求解表達式：

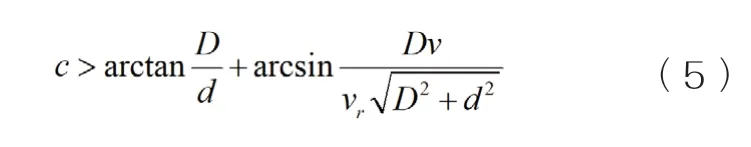
其中，行人過道角度c∈（0，90°]，c=90°表示行人僅直線過道，若求解得到c＜90°，表示行人過道時間相對充裕，可與車輛相向而行且斜行過道。對人過道角度c在各組參數變量工況進行疊合，進而得到組任意參數變量下行人過道角度c的最優解。

構建人車交互的函數關系，并進行模擬分析，關鍵函數如下：

通過選擇常見的車速和行人過道速度，利用計算機軟件編程輸入不同的人車初始水平距離即可得到與之相應的行人安全過道角度c，進而分析得到不同距離下行人的安全過道方式。

3 模型計算結果及分析

根據人車交互通行軌跡模型的數學模型，在行人與車輛距離在4~6 s時間與距離內，將表1的參數代入，分別考慮2種車道寬度和3種車輛行駛速度的組合工況。根據車速和車道寬度類別分六種情形進行模擬分析，具體工況及計算結果見表2。

表2 不同工況下人車交互通行計算結果

通過表2可知：

（1）工況1下行人經過單車道，當車輛與行人距離較近時，只要人車初始水平距離小于4 m，車輛能夠在極限相遇之前駛離，而距離較遠時，只要人車初始水平距離大于8 m行人能夠在極限相遇前安全通過。即，人車水平距離在[4，8]m時，行人極限過道角度均不小于59°，行人安全過道角度為[0，59]°。

（2）工況2下行人經過雙車道，模擬工況發現人車水平距離在[0，11]m時，行人安全過道角度均為90°，而此時行人在該工況速度較低而車能夠在行人與其有碰撞風險之前駛離，表明在距離小于11 m之前，人車過道互不影響，行人以直線90°方式過道最為高效安全。

（3）工況3下行人經過單車道，初始距離較近，只要人車初始水平距離小于20 m，車能夠在極限相遇前駛離，而距離大于33 m則行人能夠在極限相遇前安全通過。在存在碰撞風險的區段，行人極限過道角度均不小于47°，行人安全過道角度為[0，47]°，以47°斜向通行能夠在確保安全下高效過道。斜行區段為[20，33]m，不在該區段的以直線90°通行效率最高。

（4）工況4下行人經過雙車道，發現極限相遇的水平距離的區段為[43，57]m，在該區段存在碰撞風險，適合斜向通行，行人極限過道角度均不小于59°，行人安全過道角度為[0，59]°，以59°斜向通行能夠在確保安全下高效過道。不在該區段的，行人以直線90°通行效率最高。

（5）工況5下行人經過單車道，極限相遇的水平距離的區段為[35，58]m，在該區段存在碰撞風險，適合斜向通行，行人極限過道角度均不小于45°，行人安全過道角度為[0，45]°，以45°斜向通行能夠在確保安全下高效過道。不在該區段的，行人以直線90°通行效率最高。

（6）工況6下行人經過雙車道，極限相遇的水平距離的區段為[76，97]m，在該區段存在碰撞風險，適合斜向通行，行人極限過道角度均不小于57°，行人安全過道角度為[0，57]°，以57°斜向通行能夠在確保安全下高效過道。不在該區段的，行人90°直線通行效率最高。

當人車初始水平距離屬于斜向通行最高效區段時，在編程模擬運行結果中均能得到各個距離所對應的最佳高效通行角度。以工況3的數據集進行分析，當車輛以8.3 m/s行駛、行人以1.2 m/s行進，初始水平距離為20 m時，行人斜向通行最佳角度為56°，安全避讓角度為（0，56）°；初始水平距離取32 m時，行人斜向通行最佳角度為47°，安全避讓角度為（0，47）°；當初始水平距離為40 m時，最佳通行角度為90°，即行人直線通行最高效。同理可得到任意區段適用的通行方式和行人斜向過道最佳通行角度。

4 結論與展望

（1）通過建立人車交互通行數學模型，確定人車直線勻速運動下高效通行的安全通行角度計算方法，利用計算機軟件編程對6組工況進行數據仿真，得到了能夠確保安全的情況下行人直行的高效通行建議。驗證了行人成一定夾角的過道方式也能保證安全性和高效性，為道路規劃、出行方式和汽車智能自動化設計提供理論依據。

（2）對于行人過道策略的選擇仍是目前自動駕駛的難點，對多人過道或在人車變速和曲線運動下的人車交互過道仍有待繼續深化研究。