機器人TIG焊接的焊縫形貌遺傳神經(jīng)網(wǎng)絡(luò)預測

吳月玉，張 弓，林群煦，侯至丞，楊文林

（1.廣州中國科學院先進技術(shù)研究所，廣州 511458；2.五邑大學 軌道交通學院，江門 529020）

0 引言

機器人焊接是一個典型的多輸入多輸出非線性時變系統(tǒng)。焊接工藝是工業(yè)制造中不可缺少的重要組成部分[1]。鎢極惰性氣體保護焊（TIG）是最常用的弧焊工藝之一，是在惰性氣體的保護下，通過非消耗性鎢電極和工件之間產(chǎn)生電弧熔化母材和填充焊絲實現(xiàn)焊接的一種方法[2]。隨著焊接產(chǎn)品制造技術(shù)自動化、柔性化和智能化的提高，焊接工藝參數(shù)的選擇必須經(jīng)過進一步優(yōu)化，才能在給定的生產(chǎn)率下獲得理想的焊縫[3]。各焊接工藝參數(shù)之間的高度復雜耦合性使求解最佳焊接工藝成為一個難題[4]。

傳統(tǒng)的焊接工藝需要通過大量試驗制定，成本高且實驗結(jié)果不確定性很大[5]。因此，國內(nèi)外很多學者建立焊接工藝參數(shù)和焊縫幾何形狀之間的數(shù)學模型來控制和優(yōu)化焊接過程。Yang[6]等建立了多元線性回歸模型對埋弧焊的焊縫寬度、余高和熔深進行預測；Kim[7]等利用BP神經(jīng)網(wǎng)絡(luò)方法預測多道次焊接的焊縫余高和焊縫寬度；Marina[8]等利用人工神經(jīng)網(wǎng)絡(luò)預測奧氏體不銹鋼焊縫的鐵素體含量、熔寬、余高和熔深；Yin[9]等建立深度網(wǎng)絡(luò)模型對5083鋁合金雙絲CMT焊接焊縫的熔深、熔寬和余高進行預測；陳子琴[10]等用焊接特征信息圖像所提取的9組特征信息作為輸入建立含兩個隱藏層的貝葉斯神經(jīng)網(wǎng)絡(luò)對焊件背面的寬度進行預測；Yang[11]等利用決策樹和貝葉斯神經(jīng)網(wǎng)絡(luò)研究了攪拌摩擦焊氣孔形成條件；Parikshit[12]等利用遺傳算法替代BP神經(jīng)網(wǎng)絡(luò)的梯度下降法搜索神經(jīng)網(wǎng)絡(luò)的最優(yōu)權(quán)值后建立神經(jīng)網(wǎng)絡(luò)預測TIG焊接焊縫的正面高度、背面寬度、背面高度和背面寬度。雖然這些模型對焊縫形貌預測具有一定的作用，但由于影響焊縫形成的因素眾多且復雜，各個焊接工藝參數(shù)之間高度耦合，導致預測的精度不是很高且泛化能力不是很強。此外，傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)存在收斂速度慢、訓練時間長、容易陷入局部最小值的問題[13]；而利用遺傳算法替代BP神經(jīng)網(wǎng)絡(luò)的梯度下降法雖克服了BP神經(jīng)網(wǎng)絡(luò)易陷入局部最小點的問題但仍存在遺傳迭代次數(shù)多、訓練時間過長的問題。

為了解決上述問題并進一步提高焊縫形貌預測模型的預測精度和泛化能力，本文通過試錯實驗確定BP神經(jīng)網(wǎng)絡(luò)的拓撲結(jié)構(gòu)，其次利用遺傳算法確定BP神經(jīng)網(wǎng)絡(luò)初始的權(quán)值和閾值后建立TIG焊接的焊縫形貌預測模型,最后通過一些測試實例對比和驗證該模型的性能。

1 TIG焊接過程的特征參數(shù)

焊縫幾何形狀在確定焊縫的質(zhì)量方面至關(guān)重要，而焊接機器人的各個焊接工藝參數(shù)都在一定程度上影響焊縫幾何形狀的形成。圖1是TIG焊的原理示意圖[14]，圖2是TIG焊接的焊縫主要形貌幾何參數(shù)示意圖。

圖1 TIG焊原理示意圖

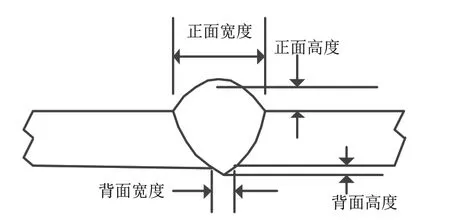
圖2 焊縫幾何參數(shù)示意圖

TIG焊接過程的輸入工藝參數(shù)（如焊接速度、送絲速度、陰極清洗率、間隙、焊接電流)與輸出焊縫的形貌幾何參數(shù)（如正面高度FH、正面寬度FW、背面高度BH、背面寬度BW）之間的映射關(guān)系如圖3所示。

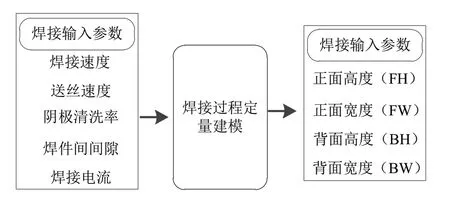
圖3 TIG焊接輸入輸出參數(shù)映射示意圖

為了提高建模的效率，本文利用全因子實驗設(shè)計(DOE)的樣本數(shù)據(jù)作為訓練模型的數(shù)據(jù)，每個輸入變量考慮兩個水平如表1所示，實驗組合為32組實驗。另外選用33組實驗數(shù)據(jù)驗證模型的預測精度和泛化能力；需要指出的是，上述所提及的訓練和測試模型的數(shù)據(jù)均是從文獻[15]中收集所得。

表1 輸入焊接參數(shù)及其范圍

2 建立GA優(yōu)化的BP預測模型

2.1 BP神經(jīng)網(wǎng)絡(luò)的建立

BP神經(jīng)網(wǎng)絡(luò)具有較強的非線性映射能力和容錯能力[16]；已被廣泛運用于各種焊接參數(shù)的非線性預測中。所建立的5輸入4輸出的TIG焊接焊縫形貌BP神經(jīng)網(wǎng)絡(luò)拓撲結(jié)構(gòu)如圖4所示。

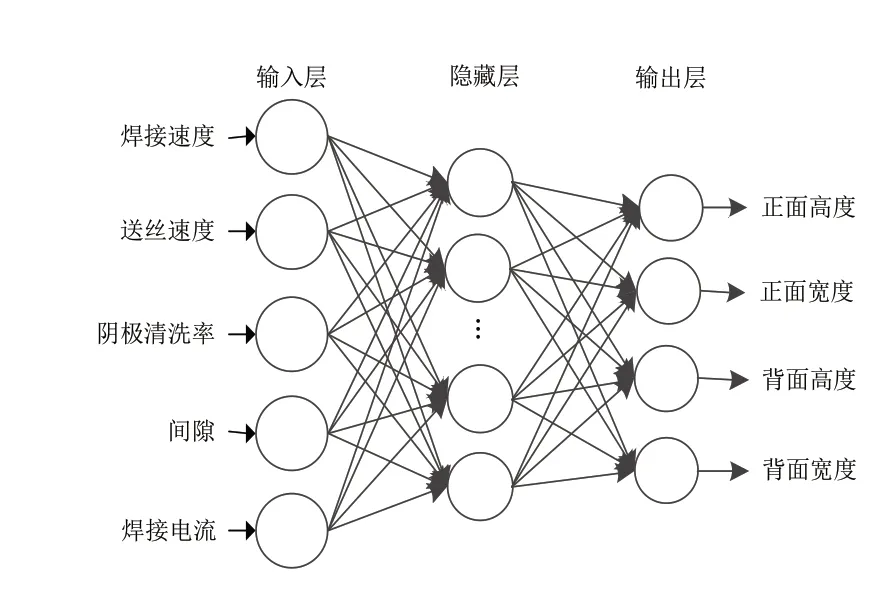
圖4 TIG焊接過程BP神經(jīng)網(wǎng)絡(luò)拓撲結(jié)構(gòu)

BP神經(jīng)網(wǎng)絡(luò)主要包含信號前向傳播和反向傳播兩個過程，每一層中特定神經(jīng)元的示意圖如圖5所示，分別為輸入層的第個神經(jīng)元、隱藏層的第個神經(jīng)元和輸出層的第個神經(jīng)元[12]，BP神經(jīng)網(wǎng)絡(luò)各層的各個神經(jīng)元的運算過程如圖5所示。

圖5 每一層中特定神經(jīng)元的示意圖

信號前向傳播具體運算過程如下：

1）位于輸入層的第j個神經(jīng)元的輸出可確定為：

其中a1是傳遞函數(shù)常數(shù)，b為偏置值，IIj為位于輸入層的第j是個神經(jīng)元的輸入。

2）位于隱含層上的第k個神經(jīng)元的輸入可計算如下：

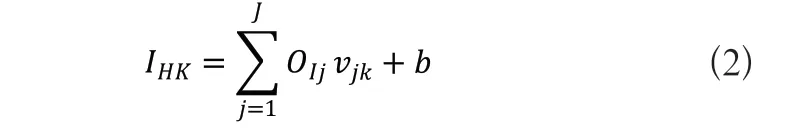
其中vjk表示輸入層第j個神經(jīng)元與隱含層第k個神經(jīng)元的連接權(quán)值。隱藏層的第k個神經(jīng)元的輸出如下：

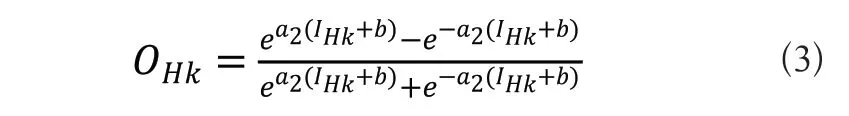
其中a2為傳遞函數(shù)常數(shù)，b為偏置值，IHk為隱藏層的第個神經(jīng)元的輸入。

3）位于輸出層的第m個神經(jīng)元的輸入如式(4)所示：

其中wkm表示隱藏層的第k個神經(jīng)元與輸出層第m個神經(jīng)元的連接權(quán)值。輸出層的第m個神經(jīng)元的輸出如式(5)所示：

其中a3為傳遞函數(shù)常數(shù)，b為偏置值，IOm為位于輸出層的第m個神經(jīng)元的輸入。

4）信號反向傳播的運算過程如下：

（1）使用隨機梯度下降算法如式(6)所示最小化損失函數(shù)：

其中J(θ)為損失函數(shù)，θ為參數(shù)，a為學習率。

（2）損失函數(shù)為：

其中p為訓練數(shù)據(jù)的個數(shù)，n為輸出向量中變量的個數(shù)。yij為輸入第i個樣本時第j個節(jié)點的期望輸出值；y′ij為輸入第i個樣本時第j個輸出節(jié)點的輸出值。

為了對神經(jīng)網(wǎng)絡(luò)進行適當?shù)挠柧毢蜏y試，訓練樣本數(shù)據(jù)和測試樣本數(shù)據(jù)所列的實驗焊接數(shù)據(jù)歸一化，歸一化范圍為[0，1]。設(shè)置Sigmoid 函數(shù)為隱藏層的傳遞函數(shù)，設(shè)置Purelin 函數(shù)為輸出層的傳遞函數(shù)，設(shè)置學習率為0.05，網(wǎng)絡(luò)訓練目標為0.01，最大迭代次數(shù)設(shè)置為20000。

為了確定BP神經(jīng)網(wǎng)絡(luò)的隱藏層的最佳神經(jīng)元節(jié)點數(shù)，在4～26之間通過試錯實驗確定，每個網(wǎng)絡(luò)重復5次，并記錄測試樣本MSE最低時所對應的網(wǎng)絡(luò)性能參數(shù)。隱藏層神經(jīng)元數(shù)目不同時所對應的網(wǎng)絡(luò)性能如表2所示，結(jié)果表明隱藏層神經(jīng)元數(shù)目的增加并不能保證均方差的降低。考慮網(wǎng)絡(luò)的泛化能力與網(wǎng)絡(luò)的逼近能力，通過對比驗證，選取隱藏層神經(jīng)元數(shù)為22即確定BP神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)為5-22-4。

表2 用于TIG焊接過程建模的各種反向傳播網(wǎng)絡(luò)

2.2 GA和BP的結(jié)合

遺傳算法（genetic algorithm，GA）是基于生物界適者生存、優(yōu)勝劣汰的進化規(guī)律實現(xiàn)全局空間優(yōu)化搜索的算法[17]，將待優(yōu)化參數(shù)轉(zhuǎn)換成編碼串聯(lián)到群體中，再按照所選擇的適應度函數(shù)對編碼的參數(shù)進行若干代的交叉、變異和選擇操作最終獲得適應度最高的個體[18,19]。

利用遺傳算法優(yōu)化反向傳播神經(jīng)網(wǎng)絡(luò)（back propagation neural network，BP）的初始權(quán)值和閾值的流程如下：

1）設(shè)置GA的種群個體數(shù)50、遺傳迭代代數(shù)為20，交叉率為0.5，變異率為0.005。根據(jù)2.1節(jié)所確定的BP神經(jīng)網(wǎng)絡(luò)網(wǎng)絡(luò)設(shè)置各層的初始權(quán)值和閾值的個數(shù)（如表3所示）后按實數(shù)編碼的方式將其對應于染色體每個基因位；然后將[-0.5，0.5]之間的數(shù)值隨機賦予BP神經(jīng)網(wǎng)絡(luò)的連接權(quán)值和閾值即生成初始種群。

表3 BP神經(jīng)網(wǎng)絡(luò)的權(quán)值和閾值的個數(shù)

2）利用神經(jīng)網(wǎng)絡(luò)訓練樣本的均方差的倒數(shù)計算GA當前種群的每個個體的適應度值，即：

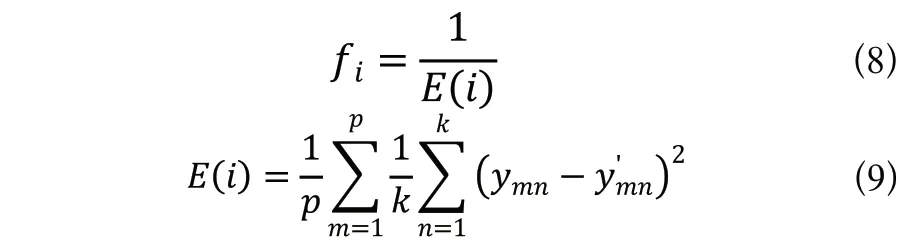
其中，fi為個體i的適應度值；k為輸出層節(jié)點數(shù)；ymn為輸入第m個樣本時第n個節(jié)點的期望輸出值；y′mn為輸入第m個樣本時第n個輸出節(jié)點的輸出值。

3）重復進行選擇、交叉、變異操作達到20次后將最優(yōu)個體所對應的值分解后賦給BP神經(jīng)網(wǎng)絡(luò)作為它的初始權(quán)值和閾值；最后導入訓練樣本對BP神經(jīng)網(wǎng)絡(luò)進行訓練并保存最優(yōu)的BP神經(jīng)網(wǎng)絡(luò)模型。

4）利用測試樣本對所保存的網(wǎng)絡(luò)模型的預測精度和泛化能力進行測試和驗證。

3 焊縫形貌的預測

3.1 訓練網(wǎng)絡(luò)模型

將訓練樣本歸一化后導入到GA-BP網(wǎng)絡(luò)模型中進行訓練。尋找最優(yōu)適應度個體過程中種群的平均適應度值的變化如圖6所示，平均適應度值隨著遺傳進化代數(shù)的增加而增大，在第11代時平均適應度值最大，進化到20代時停止遺傳操作。將最優(yōu)個體分解后賦給BP神經(jīng)網(wǎng)絡(luò)作為初始權(quán)值和 值后訓練BP神經(jīng)網(wǎng)絡(luò)，優(yōu)化后的BP神經(jīng)網(wǎng)絡(luò)訓練過程的損失函數(shù)變化如圖7所示，網(wǎng)絡(luò)訓練到401步時達到要求的訓練精度，迭代訓練終止。

圖6 平均適應度值變化曲線

圖7 訓練誤差變化曲線

3.2 仿真驗證與分析

為了檢驗本研究建立的GA-BP的TIG焊接的焊接工藝參數(shù)與焊縫形貌關(guān)系回歸模型的性能，采用傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)（BP）、遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)（GA-BP）進行對比試驗。兩種算法中的BP神經(jīng)網(wǎng)絡(luò)的訓練模型的目標精度均為0.01，學習率均為0.05；將訓練樣本進行歸一化處理后分別導入BP神經(jīng)網(wǎng)絡(luò)模型和GA優(yōu)化后的BP網(wǎng)絡(luò)模型中進行訓練后并保存最優(yōu)模型；再將測試樣本進行歸一化處理后導入到所訓練好的兩種模型中，最后將預測結(jié)果進行反歸一化處理即可得到對應焊縫的正面高度FH、正面寬度FW、背面高度BH、背面寬度BW的預測值，預測結(jié)果如圖8所示。表4為BP神經(jīng)網(wǎng)絡(luò)模型和GA-BP神經(jīng)網(wǎng)絡(luò)模型的決定系數(shù)表，表5為BP神經(jīng)網(wǎng)絡(luò)模型、GA-NN神經(jīng)網(wǎng)絡(luò)模型和GA-BP神經(jīng)網(wǎng)絡(luò)模型的平均絕對百分比誤差表。

由圖8可以看出BP神經(jīng)網(wǎng)絡(luò)模型和GA優(yōu)化的BP網(wǎng)絡(luò)模型都能較好地預測TIG焊接的焊縫主要形貌參數(shù)；通過表4和表5的數(shù)據(jù)分析可知，遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)模型測試得到的平均絕對百分比誤差比較小，且決定系數(shù)比較大，說明遺傳神經(jīng)網(wǎng)絡(luò)預測效果優(yōu)于傳統(tǒng)BP神經(jīng)網(wǎng)絡(luò)，預測精度更高，泛化能力更強，選用遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)模型可以建立更有效的TIG焊接的焊接工藝參數(shù)與焊縫形貌關(guān)系回歸模型。

圖8 預測效果對比圖

表4 兩種模型決定系數(shù)（R2）表

由表5可知本方法訓練時只需經(jīng)過20次遺傳迭代獲取初始權(quán)值和閾值后結(jié)合BP神經(jīng)網(wǎng)絡(luò)的401次梯度下降迭代訓練達到均方差目標為0.01時，同一測試集的部分響應可比文獻[8]中的GA-NN預測方法所預測的FH、FW、BW的平均絕對百分比誤差分別減少12.057%、5.442%、6.703%，適應性更強，預測精度更高。GA-BP焊縫形貌預測結(jié)果的優(yōu)劣在很大程度上取決于BP網(wǎng)絡(luò)的好壞。由于多輸出BP神經(jīng)網(wǎng)路的損失函數(shù)的局限性，所預測的背面高度BH的預測精度有待提高。后期可通過改進損失函數(shù)和優(yōu)化網(wǎng)絡(luò)訓練集等方式對模型的訓練過程進行優(yōu)化提高BH的預測精度。

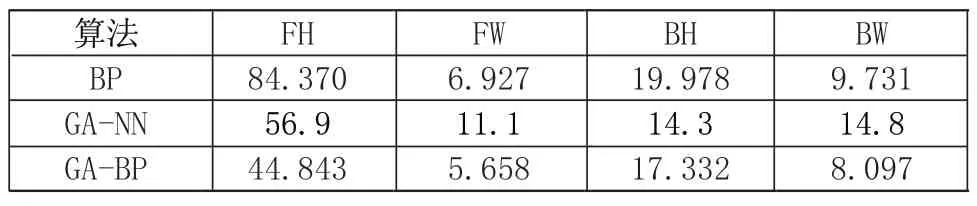
表5 三種模型平均絕對百分比誤差（MAPE）

4 結(jié)語

1）利用全因子實驗設(shè)計可以大量減少試驗次數(shù)和訓練的樣本容量，保持其代表性的同時減少訓練模型所需的時間。

2）仿真驗證結(jié)果表明，與傳統(tǒng)的BP神經(jīng)網(wǎng)絡(luò)相比，通過遺傳算法優(yōu)化BP神經(jīng)網(wǎng)絡(luò)的初始權(quán)值和閾值后的BP神經(jīng)網(wǎng)絡(luò)模型的預測精度更高，適應性更強，能有效預測TIG焊接的形貌特征參數(shù)。

3）根據(jù)本研究建立的TIG焊接的焊接工藝參數(shù)與焊縫形貌關(guān)系回歸模型可以較好地預測TIG焊接的焊縫正面高度、正面寬度、背面高度和背面寬度，從而為TIG焊接地焊接工藝參數(shù)調(diào)優(yōu)提供理論基礎(chǔ)。