雙高箱集裝運輸線路接觸網-受電弓適應性研究

孫立金，時恒明，羅 群，呂青松，劉 暢，喬 維

0 引言

具有低能耗、高效率等優勢的鐵路運輸是交通強國戰略的重要組成部分[1]，為連接“一帶一路”沿線各國及各區域發揮紐帶作用。隨著經濟的快速發展，迫切需要更為高效的鐵路集裝箱運能方式，為此，國家制定了推進發展雙層集裝箱運輸規劃[2]。由兩個高箱疊裝的雙高箱集裝運輸不但節約運營成本，同時減少跨國高箱運輸更換箱體的步驟[3]，能夠大幅提升運輸效率。為更好地展現鐵路運輸優勢、發展多式聯運，有必要對雙高箱集裝運輸系統進行研究。

受電弓-接觸網系統為列車運行提供能量，受電弓將接觸網系統中電能傳輸到列車（受流），為牽引電機提供動力，列車能夠安全穩定運行的前提是具有良好的受流質量[4，5]。在取流過程中，受電弓與接觸線之間存在一定的接觸壓力，當接觸壓力保持合適即匹配的弓網系統動力學特性時，才能保證其受流質量，因此，必須對弓網系統的動力學特性展開研究[6]。對于雙高箱集裝運輸線路如金甬線，接觸網導線高度已達到6 680 mm，國內外均缺少在該條件下的弓網系統動力學特性研究[7]。為合理組織跨線運行[8]，對動車組通過雙高箱集裝運輸線弓網適應性問題的研究同樣不可忽視。

本文將針對金甬雙高箱集裝運輸線路接觸網系統展開電力機車運輸時以及動車組跨線運行時的弓網系統動力學特性研究，以弓網系統間的接觸力各統計數值分析其適應性。在保證受電弓取流的情況下，選取HXD2B、FXD1（貨運機車）及CHR6A（動車組）3種車型所搭載的對應型號受電弓展開弓網受流質量分析，可為雙高箱集裝運輸線路以及跨線運行的弓網適應性研究提供一定參考。

1 模型建立及驗證

1.1 接觸網模型

準確建立接觸網系統模型是進行弓網系統動力學研究的前提條件，接觸網建模有兩種常用方法：通過計算接觸網振動模態的模態疊加法[9，10]和基于空間有限元法的直接建模法[11，12]。由于直接建模法具有建模方式簡單、精度高等優點，本文將采用該方法對接觸網系統進行建模。首先，根據接觸線、承力索以及吊弦間連接關系及邊界條件采用歐拉梁單元建立初始接觸網模型；其次，通過分模法[13]獲取接觸網系統的關鍵節點信息，即完成接觸網找形；最后，根據接觸網系統的關鍵節點信息建立仿真初始模型，其中吊弦由于其工作特性使用非線性彈簧單元模擬[14]。

金甬雙高箱集裝運輸線路接觸網采用簡單鏈形懸掛方式，結構高度為1 400 mm，其具體參數如表1所示，與文獻[7]不同的是將接觸網系統張力體系改為15/20 kN。

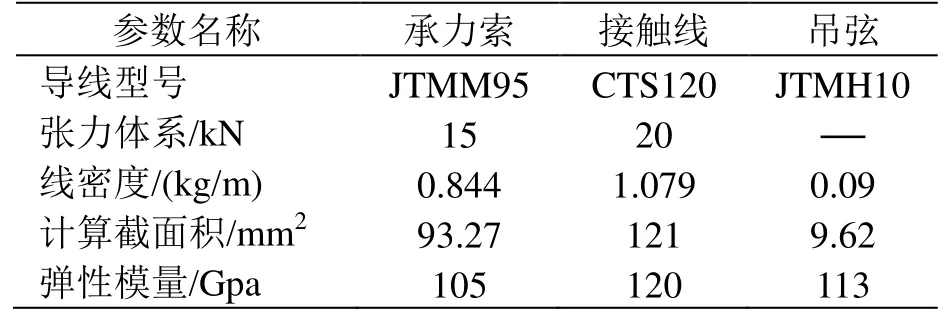
表1 金甬雙高箱集裝運輸線路接觸網參數[7]

依照上述建模方法完成接觸網系統模型搭建后，接觸網的運動微分方程可表示為

式中：M、C、K分別表示接觸網系統的質量、阻尼和剛度矩陣，Y表示各單元節點位移組合矩陣，F則為接觸網外載荷矩陣。

1.2 受電弓模型

針對不同的研究需求，受電弓建模可處理為不同的模型，其中多剛體系統更接近實際，進而本文將受電弓處理為多剛體系統。受電弓多剛體系統又可分為受電弓弓頭部分及框架部分，其中框架部分由下臂桿、上框架、拉桿和平衡桿組成，各桿件之間通過鉸接組成只由升弓角θ表示的單自由度系統。框架部分的動力學方程可寫為[15]

式中：Ak、qk、Bk分別為框架系統的系數、坐標向量以及廣義載荷向量矩陣，Φk為鉸接約束方程雅可比矩陣，λk為其對應的拉格朗日乘子。

參考文獻[15]，弓頭部分的動力學方程可寫為

式中：Mh、Yh、Fh分別表示弓頭系統的質量、位移和載荷矩陣。

因此，可得受電弓多剛體系統的動力學方程：

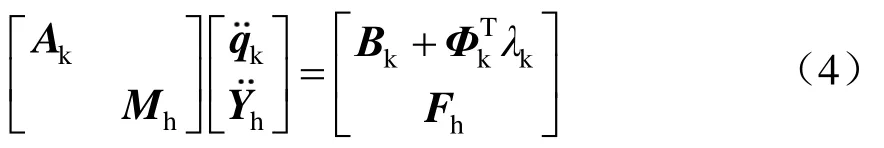
1.3 弓網耦合模型

弓網系統通過接觸力耦合，常通過線性接觸剛度并結合罰函數法計算接觸壓力[16]，接觸模型及其示意圖如圖1所示。

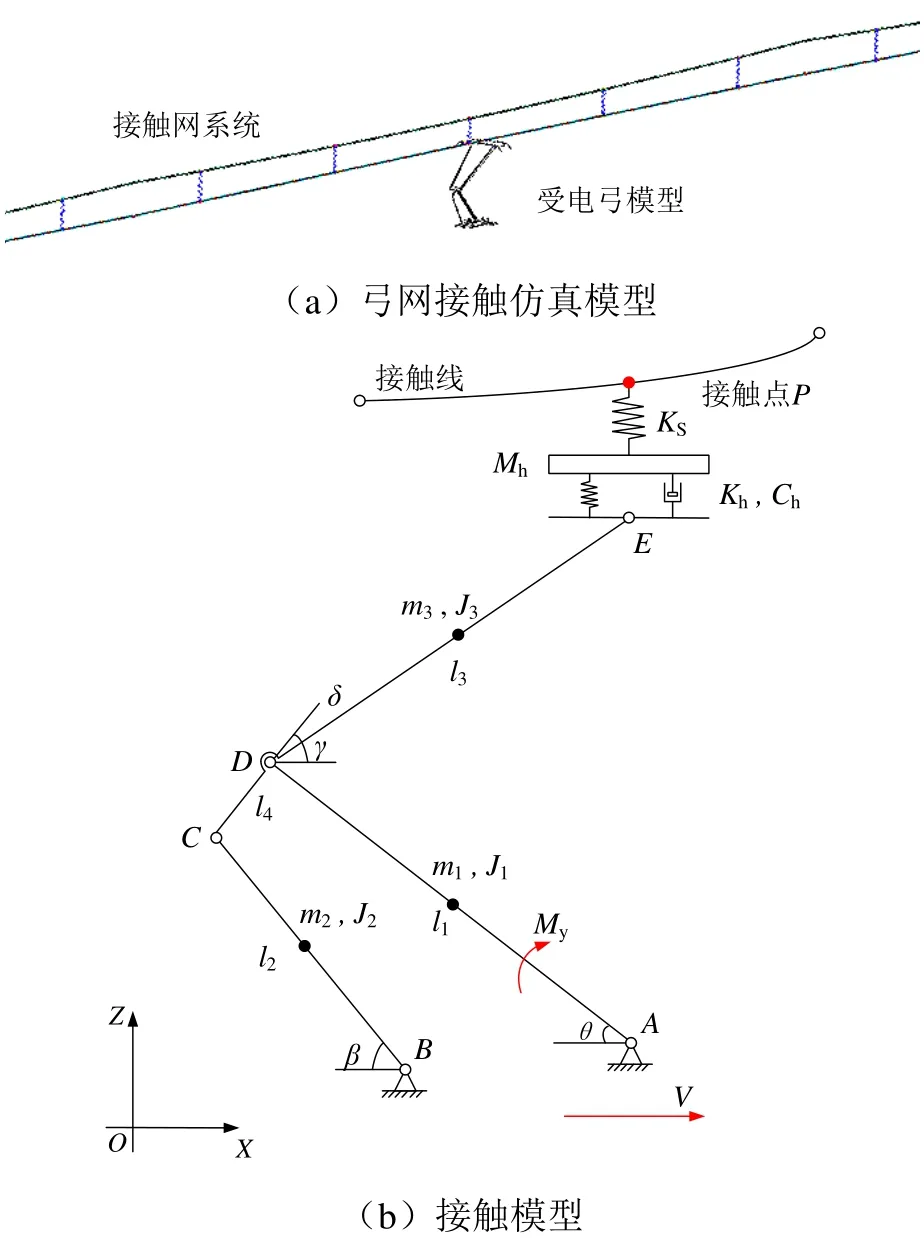
圖1 弓網系統接觸模型

設接觸點P的垂向位移為zc，則接觸力可寫為

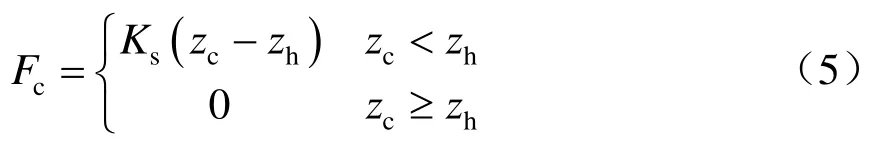
式中：Ks為接觸剛度，取50 000 N/m[17]；zh為弓頭相對位移。

1.4 模型驗證

對于弓網系統仿真，歐洲標準 EN 50318—2018[17]提供了雙弓系統仿真模型的建立方法可行性驗證，依照本文方法建立該標準中受電弓-接觸網仿真驗證模型。將速度級275 km/h仿真結果與標準中參考數值進行對比，結果見表2。可以看出，各參數統計結果均在標準范圍內，即驗證了本文方法的可行性。

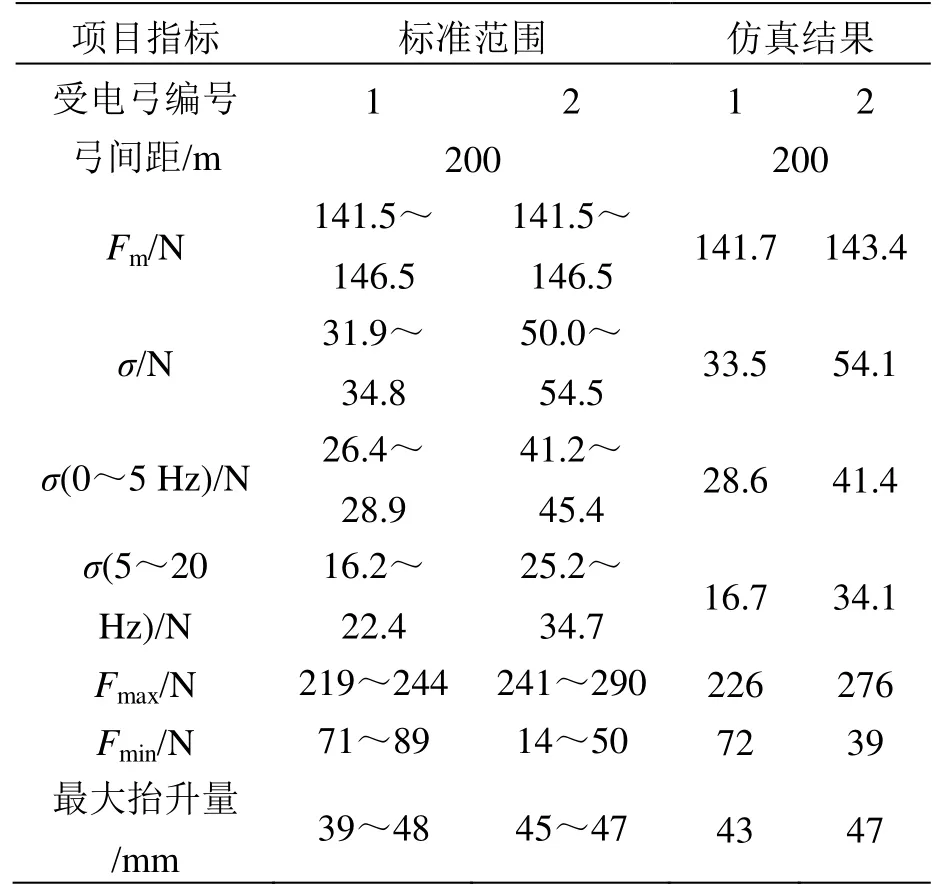
表2 模型驗證結果對比

2 仿真結果分析

針對金甬雙高箱集裝運輸線路接觸網系統，為分析電力機車如HXD2B、FXD1（貨運機車）運輸時以及動車組如CHR6A跨線運行時的弓網動力學特性，依據本文建模方法，分別建立接觸網模型以及對應受電弓模型進行仿真計算，通過計算結果中弓網系統間的接觸力各統計數值分析其適應性。

接觸力各統計數值與標準TB/T 3271—2011[18]中指標進行對比，主要包括對接觸力均值Fm、標準偏差σ、統計最大值、統計最小值的對比，各統計數值標準指標如下：

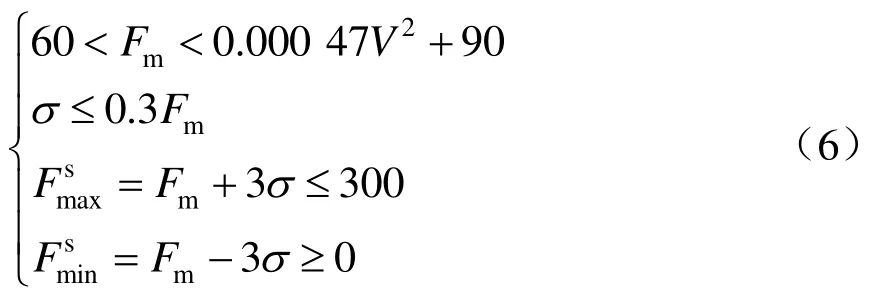
式中：V為運行速度。

金甬雙高箱集裝運輸線路設計時速為160 km，預留時速200 km條件，各車型搭載的受電弓詳細信息以及規劃計算工況如表3所示，其中受電弓工作高度包含絕緣子高度。

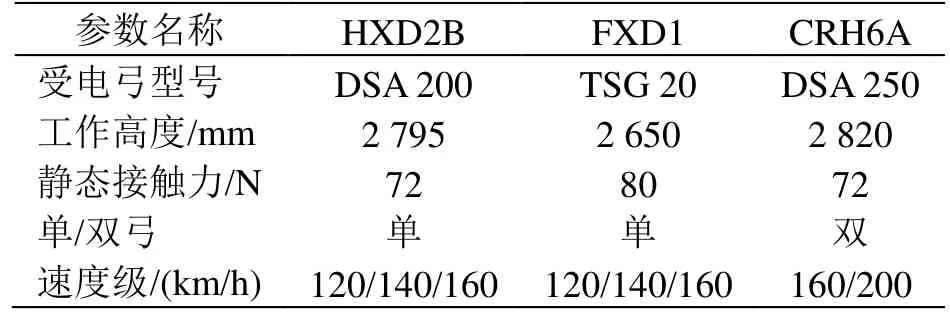
表3 受電弓型號詳細信息及計算工況設置

2.1 DSA 200型受電弓仿真結果

由表3可知，車型HXD2B所搭載的DSA 200型受電弓工作高度為2 795 mm，靜態接觸力為72 N，各速度級仿真結果如圖2所示。

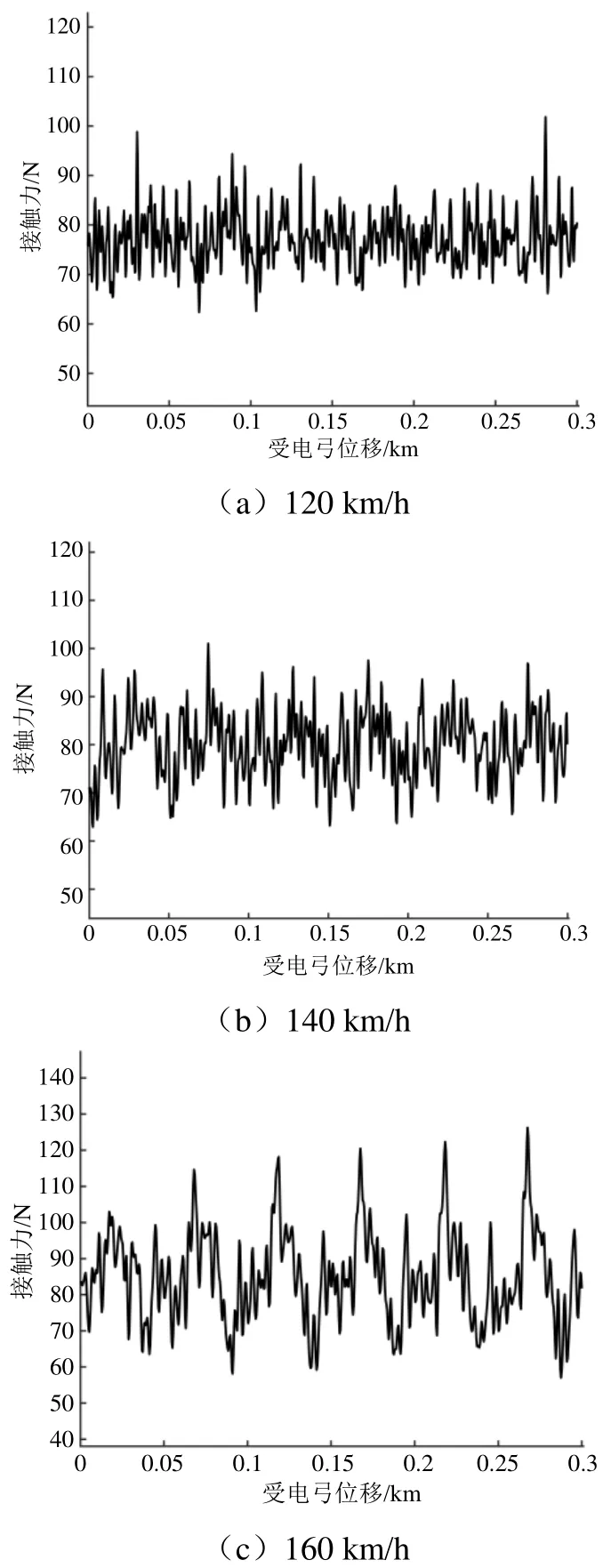
圖2 DSA 200型受電弓各速度級仿真結果

將DSA 200型受電弓各速度級下接觸力仿真結果進行統計并計算各統計數值，得到表4。可以看出，隨著速度級的增加，弓網系統間接觸力均值、標準偏差呈現增加的趨勢，即受流質量相對變差。同時，對比式（6）各指標，接觸力均值、標準偏差、統計最大值以及統計最小值均處于標準范圍內，未出現受電弓離線情況，受流質量良好，即 DSA200型受電弓與金甬雙高箱集裝運輸線接觸網系統匹配適應性良好。

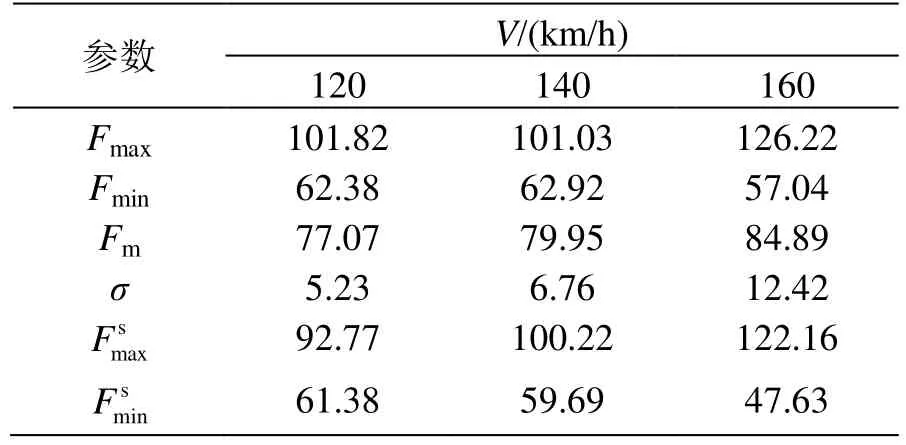
表4 DSA 200型弓網動力學統計值 N

2.2 TSG 20型受電弓仿真結果

車型FXD1所搭載的TSG 20型受電弓工作高度為2 650 mm，靜態接觸力為80 N，各速度級仿真結果如圖3所示。

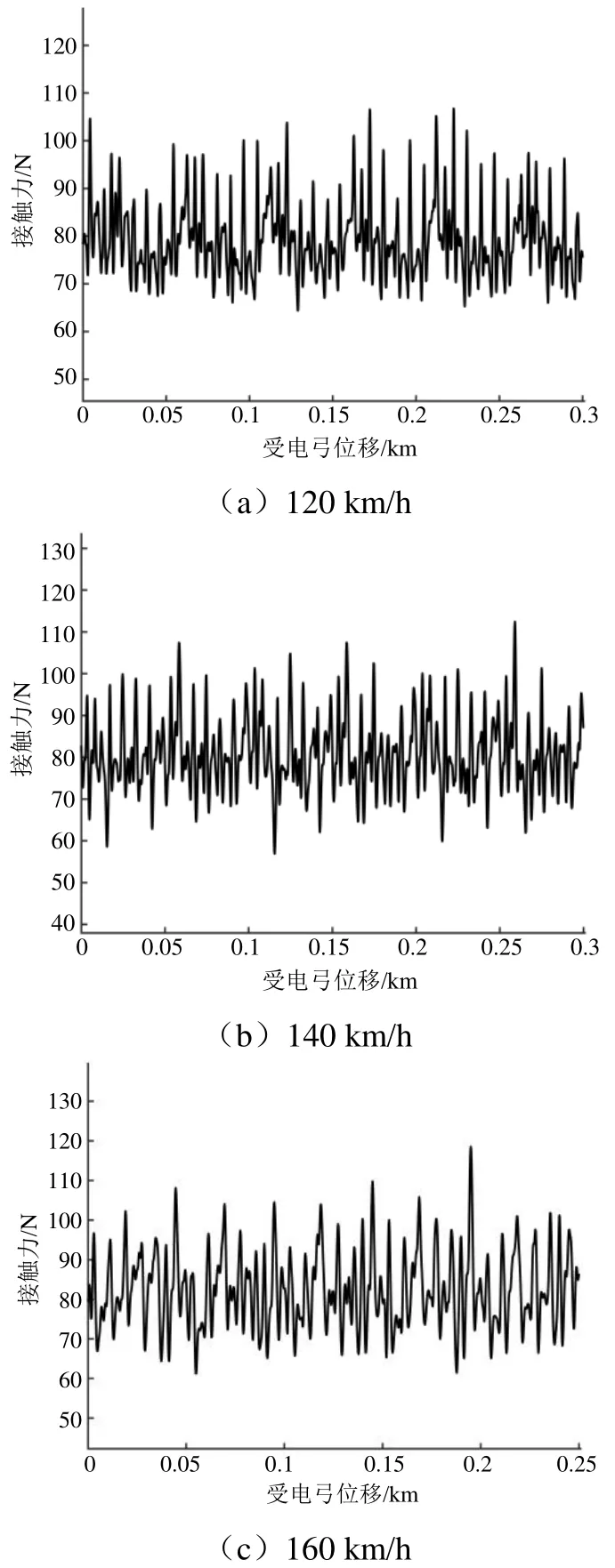
圖3 TSG 20型受電弓各速度級仿真結果

將TSG 20型受電弓各速度級下接觸力仿真結果進行統計并計算各統計數值，得到表5，其均值、標準偏差也呈現隨速度增加而增加的趨勢。同樣對比式（6）各指標，該型號受電弓弓網動態接觸力均值、標準偏差、統計最大值以及統計最小值均處于標準范圍內，未出現受電弓離線情況，受流質量良好，即TSG 20型受電弓與金甬雙高箱集裝運輸線接觸網系統匹配適應性良好。

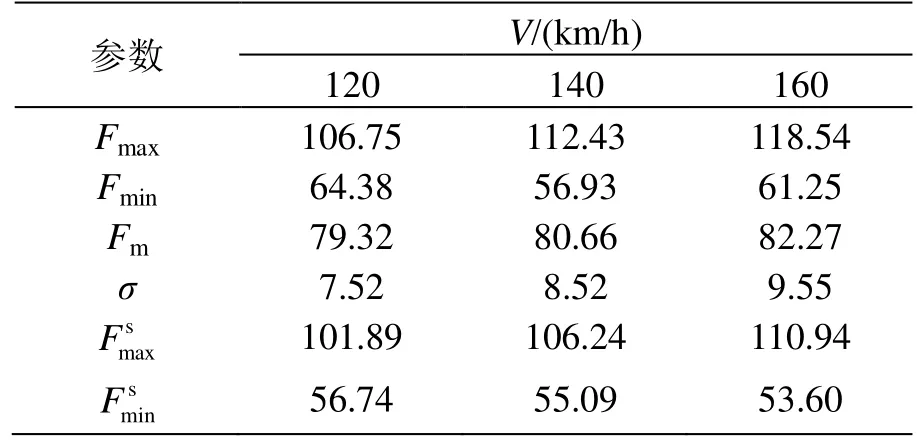
表5 TSG 20型弓網動力學統計數值 N

2.3 DSA 250型受電弓仿真結果

上述已完成兩種型號的貨運機車搭載受電弓的弓網系統受流質量評估，即金甬雙高箱集裝運輸線路上貨物運輸車型的弓網關系適應性研究，下文將針對跨線運行動車組 CRH6A車型搭載的 DSA 250型受電弓展開弓網關系適應性研究。根據表3，DSA 250型受電弓在金甬雙高箱集裝運輸線路上工作高度為2 820 mm，且為雙弓受流，靜態接觸力為72 N，其中雙弓間距為210 m。各速度級仿真結果如圖4所示。

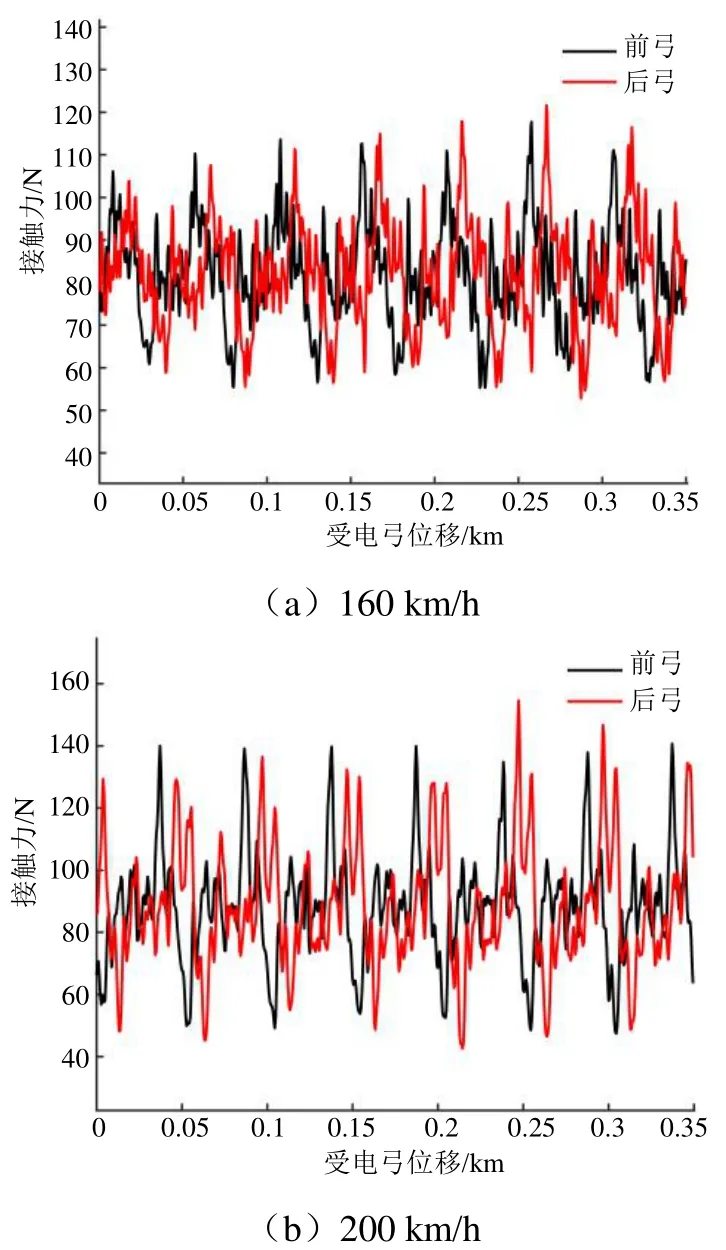
圖4 DSA 250型受電弓各速度級仿真結果

獲取雙DSA 250型受電弓系統各速度級下接觸力仿真結果并相應計算各統計數值，匯總得到表6。可以看出：在同一速度級時，后弓接觸力均值與前弓基本一致，標準偏差小幅增加，即后弓受流質量稍差于前弓受流；速度級增加時，接觸力均值、標準偏差也呈增加趨勢，但各統計數值均處于標準范圍內，未出現受電弓離線情況，受流質量良好。即DSA 250型受電弓雙弓系統跨線運行與金甬雙高箱集裝運輸線接觸網系統匹配適應性良好。

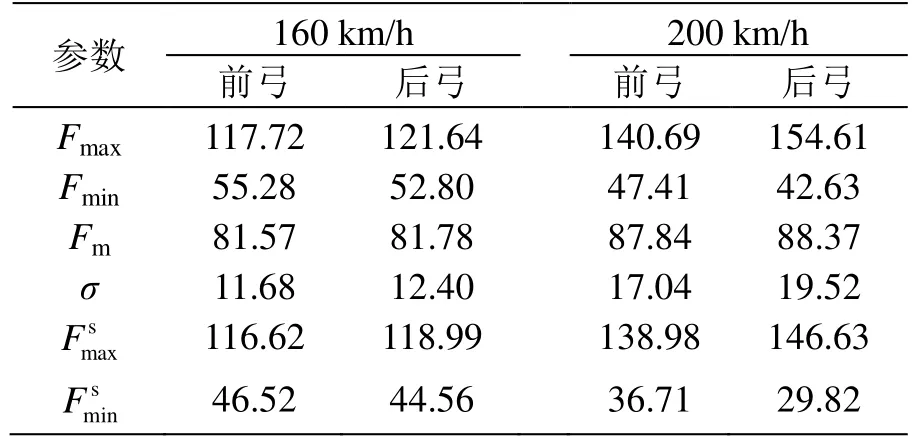
表6 DSA 250型弓網動力學統計數值 N

3 結論

本文對DSA 200、TSG 20及DSA 250型受電弓在單、雙弓條件下與金甬雙高箱集裝運輸線路接觸網系統的弓網動力學特性進行研究，將弓網間接觸力仿真結果各統計數值與相關標準對比，分析其弓網適應性，為雙高箱集裝運輸線路及跨線運行的弓網適應性研究提供一定的理論依據。結果表明：

（1）單弓受流時，DSA 200、TSG 20型受電弓接觸力均值、標準偏差均呈現隨速度級增加而增加的趨勢，即弓網受流質量隨速度增加而降低，但各統計數值均處于標準參考值范圍內，受流質量以及弓網適應性良好。

（2）雙弓受流時，DSA 250型受電弓在同一速度級下，后弓接觸力均值與前弓基本一致，但標準偏差小幅增加，即后弓受流質量稍差于前弓受流，不同速度級下接觸力均值、標準偏差變化與單弓受流的趨勢一致，且均處于標準范圍內，前、后弓受流質量及弓網系統適應性均良好。