混合模式磁流變阻尼器的機械腿減振控制

楊坤全，黃惠

(1.漳州職業技術學院汽車工程系，福建 漳州 363000；2.福州大學機械工程及自動化學院，福建 福州 350108)

0 引言

機器人是多學科交叉和技術綜合的結晶[1],目前在生產、運輸、軍事等領域都發揮著重大作用.其中足式機器人因具有更接近生物的行動方式、較強的環境適應能力、可代替人類開展復雜且危險的工作、節約人力成本[2]等特征，而擁有廣闊的應用前景.但實際使用過程中，機械腿在高速、重載、跳躍、崎嶇道路等情況下，會發生很大的振動，影響到工作的穩定性.如何消除或抑制振動以保證機器人的穩定性是足式機器人研究的關鍵問題之一[3].目前使用的減振控制方法主要有被動減振控制、主動減振控制和半主動減振控制.

被動減振控制的原理是在系統中加入阻尼元件來吸收振動能量并轉化為其他形式，或者改變結構使得系統質量得到優化分布而實現減振效果[4].常采用的方法有：在機器人腳底安裝橡膠、泡沫[5-6]一類的軟質材料或彈簧緩沖裝置[7-8]來減小地面沖擊，又或者模仿人腳的生理結構，在腳的側面和后部擴大穩定支撐區域[9].雖然被動減振系統性能穩定、易于維護、針對高頻振動減振效果較好，但其結構一旦確定，只對固定頻率的振動起作用[6]，難以適應某些足式機器人的復雜工作場所.主動減振控制需要外部能源輸入提供控制力，控制過程依賴于結構反應和外界干擾信息，具有適應范圍廣、控制效果好等特點，但其控制系統結構復雜，造價昂貴.而半主動控制綜合了前兩者的優點[10]，其中，磁流變阻尼器具有響應速度快、阻尼可調范圍大、能耗較低等優勢，是當前振動控制領域的研究熱點[11].戴金橋等[12]使用磁流變阻尼器實現對柔性機器人關節振動的半主動控制，蔣楠[13]設計了一種旋轉型磁流變液阻尼并將其應用于機器人腿中，通過不同的電流控制策略調整機器人腿與地面的相互作用，實現運動過程中的半主動控制.然而這些磁流變阻尼器的出力效果仍無法滿足機械腿在特殊工況下的減振需求.

因此，本研究提出一種剪切閥-擠壓混合模式磁流變阻尼器對機械腿進行減振控制的方法.該新型阻尼器相較傳統磁流變阻尼器而言具有更大的出力，在阻尼通道處具有更為均勻的磁場分布以及更高的磁感應強度.在剛性地面與柔性地面之間，依靠模式切換可快速提供連續可調的阻尼力，滿足足式機器人對復雜工作場所的減振需求.對該阻尼器進行動力學臺架試驗獲取其動力學數據，建立其 Bouc-Wen 模型，基于遺傳算法對模型參數進行辨識，建立機械腿的Simulink仿真模型，并采用天棚控制的方法進行減振控制，為足式機器人的機械腿減振提供了一種方法.

1 新型混合式磁流變阻尼器介紹

將現有的一種新型剪切閥-擠壓混合模式磁流變阻尼器應用于機械腿減振控制，其結構如圖 1所示，主要結構的尺寸參數，如圖2所示.

圖1 新型混合模式磁流變阻尼器結構Fig.1 New hybrid mode magnetorheological damper

圖2 新型混合模式磁流變阻尼器主要結構尺寸(單位：mm) Fig.2 Main structural dimensions of new hybrid mode magnetorheological damper(uint:mm)

該阻尼器具體性能可參考前期研究[14].該阻尼器的重點創新設計在于：活塞和缸筒處都安裝了兩組勵磁線圈，實現磁流變阻尼器在兩種工作模式的轉換.當在一般較輕負載的情況下，只給活塞線圈通入電流，不給套筒線圈通入電流，該閥處于剪切閥式的工作模式.在特定的極端負載的情況下，給活塞處和套筒處的線圈同時通入電流，此時該閥處于剪切閥-擠壓式的工作模式，活塞桿向外輸出較大的阻尼力.此款新型混合式磁流變阻尼器，可根據不同的場景，通過控制輸入電流的大小，控制阻尼器的最大輸出力，符合足式機器人對復雜工作情況的需求.

2 混合式磁流變阻尼器正模型

2.1 混合式磁流變阻尼器力學實驗

為獲取該混合模式磁流變阻尼器的力學數據，利用萬能材料試驗機進行測試，對活塞線圈和缸筒線圈分別提供不同的電流激勵，測試阻尼器在不同工作模式下的力學性能，萬能材料試驗機測試現場如圖3所示.

圖3 阻尼器力學性能測試Fig.3 Mechanical performance test of damper

設置激勵信號為正弦輸入信號，當測試線圈分別通入 0.1，0.3，0.6，1.0 A電流時，剪切閥式下力與位移的關系如圖4所示.實驗結果表明，混合式阻尼器在剪切閥式下，對活塞兩線圈施加1.0 A電流時阻尼器的最大出力可達1.065 kN；當測試線圈分別通入 0.1，0.3，0.6，1.0 A電流時，剪切閥-擠壓模式下阻尼器力與位移的關系如圖5所示.從圖5中可見，剪切閥-擠壓式阻尼力位移滯回曲線與剪切閥式阻尼力位移滯回曲線有所不同，剪切閥-擠壓式在兩端有尖角現象.主要原因是在剪切閥-擠壓式下，磁流變液與活塞相互作用時會出現拉伸和壓縮狀態，從而導致尖角現象的發生.試驗測試結果表明，當只給兩線圈施加1.0 A電流時，混合式阻尼器在剪切閥-擠壓式下最大出力可達4.939 kN.相比單一形式的磁流變阻尼器，混合式阻尼器可以使阻尼力的最大出力增加364%.

圖4 剪切閥式下阻尼器力與位移曲線Fig.4 Force and displacement curves of damper under shear valve type

圖5 剪切閥-擠壓模式下阻尼器力與位移曲線Fig.5 Damper force and displacement curves in shear valve-squeeze mode

2.2 混合式磁流變阻尼器模型識別

由于磁流變液體的非線性，選用Bouc-Wen模型作為磁流變力學模型，它是目前應用最為廣泛的非線性滯回模型，通過改變模型參數就可以模擬眾多的滯回特性.該模型由滯回系統、彈簧和阻尼器并聯而成，如圖6所示.其模型方程可表示為：

圖6 阻尼器力學性能測試Fig.6 Schematic diagram of Bouc-Wen model

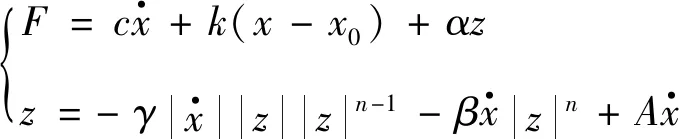
(1)

由于Bouc-Wen力學模型具有多個未知參數、運算較為復雜，本研究采用遺傳算法進行模型參數的識別工作.具體分為如下6個步驟：

1) 通過分析具體問題采用不同的編碼方式獲得初始種群；

2) 利用適應度函數計算出個體的適應度值；

3) 通過對個體適應度值進行評估將滿足條件的個體遺傳到下一代；

4) 在計算過程中設置一定比例作為種群的交叉概率遺傳到下一代；

5) 設定種群中一定的變異概率，將新得到的種群再次進行適應度計算；

6) 對種群適應度值進行評估滿足條件計算結束，否則繼續對種群執行選擇交叉變異直至收斂為止.

首先將混合式磁流變阻尼器試驗數據進行稀釋得到遺傳算法的初始種群，確定初始種群的個數為N=40.基于上述實驗位移幅值，對頻率f=5 Hz時0～1 A的試驗數據進行參數辨識，將辨識后得到的參數值代入所選的力學模型進行仿真.通過對比試驗數據與仿真結果的吻合情況，來確定參數辨識結果的正確性.采用仿真值與實驗值之差的最小平方值為適應度值，得出適應度函數具體的數學表達式為：

(2)

式中:fitness為適應度值；Fi，仿真值為第i個點的仿真值；Fi，實驗值為第i個點的實驗值;Fmax為初始種群中試驗數據的最大值；Fmin為初始種群中試驗數據的最小值；m為初始種群的個數.

滯回力模型：

滯回位移模型:

式中：由于試驗中有具體的激勵信號，因此活塞的相對位移x、相對速度v都能確定;n表示滯回曲線的圓滑程度，根據前人的研究經驗設n=2;模型中的未知參數有c、k、α、γ、β、A共6個.

在確定好適應度函數之后，設置交叉、變異比例分別是75%和25%.在初次參數辨識求出一組未知參數值后，找出每個參數的變化范圍，并將每個參數的最大值與最小值用來設置下次參數辨識的上下限，多次重復以上步驟直到每個參數達到預期精度.

2.3 辨識結果分析與驗證

1) 剪切閥式下的辨識結果.在對初始種群辨識后得到參數的最小值作其參數LB，最大值作為其參數UB，不斷重復上述操作.從而縮小模型未知參數的取值范圍，因此最終參數識別的精度也不斷提高.經過多組運算后得到的各參數值如表1所示.

表1 剪切閥式下各參數辨識結果Tab.1 Parameter identification results of shear valve type

2) 剪切閥-擠壓模式下的辨識結果.混合模式下剪切閥-擠壓模式辨識結果如表2所示.給活塞和缸筒內4個線圈同時通電，當活塞運動到缸筒中間時，形成剪切閥式；當活塞運動靠近左右端蓋時，將會形成剪切閥-擠壓式，此時阻尼力將會瞬間增大.因此在這種混合模式下，需要做兩次參數辨識工作，但活塞運動到缸筒中間可近似看成只給兩線圈通電時的普通剪切閥式，因此在混合模式下只需要對剪切閥-擠壓式進行參數辨識，辨識過程和方法與普通剪切閥式類似.

表2 剪切閥-擠壓式下各參數辨識結果Tab.2 Parameter identification results of shear valve-extrusion type

通過遺傳算法參數辨識得出的模型可以適用固定電流下，但不能適用于一般情況，因此參數辨識的結果只能接近真實值無法等于真實值.為了找出精確的模型通用表達式，可根據劉永強等[15]將c、k、α看成與電流的函數關系，β、γ、A看成為某常數對該力學模型進行改進，將Bouc-Wen模型中的c、k、α表達成電流的二次函數關系，即：

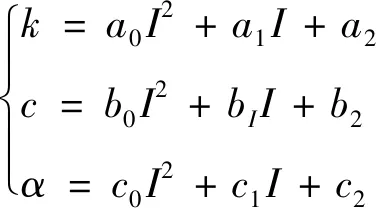
(3)

結合Bouc-Wen力學模型將其表達為：

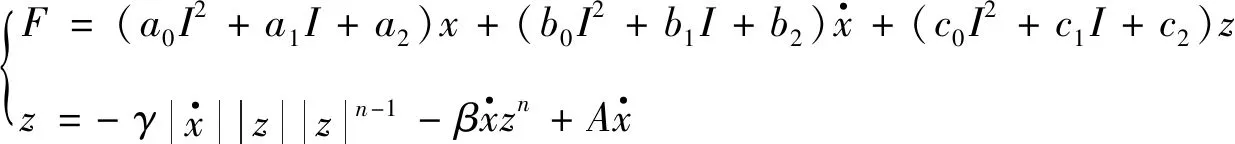
(4)

將阻尼器在不同電流下的試驗數據作為遺傳算法的初始種群，以式(4)力學模型利用遺傳算法對其進行參數辨識，得出a0、a1、a2、b0、b1、b2、c0、c1、c2、γ、β、A的值.混合式MRF阻尼器通過參數辨識.

在剪切閥式下辨識結果為：

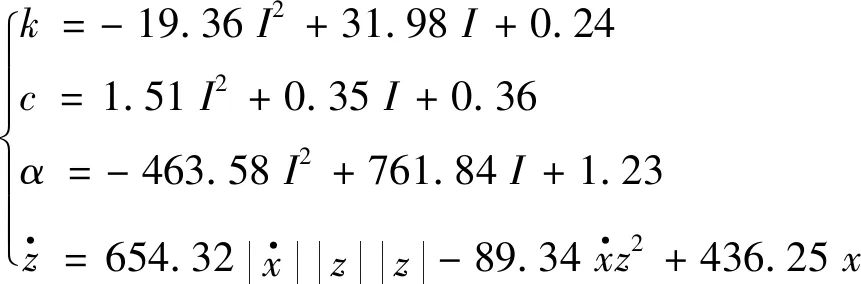
(5)

在擠壓模式下辨識結果為：

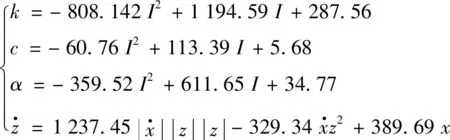
(6)

為檢驗采用遺傳算法參數辨識得出的未知參數值是否正確，將在不同電流作用下得到的參數值帶入力學模型中進行仿真,如圖7，圖8所示，并與試驗數據進行對比.從圖7、圖8中可知，在阻尼力-位移曲線中實驗值(點線)和模型預測值(實線)沒有完全吻合.因為Bouc-Wen并不是磁流變液真實力學模型，但基本能夠表達磁流變液的力學特性，在圖中具有較高的吻合度，因此得出采用遺傳算法參數辨識求解出的參數值是相對準確的.

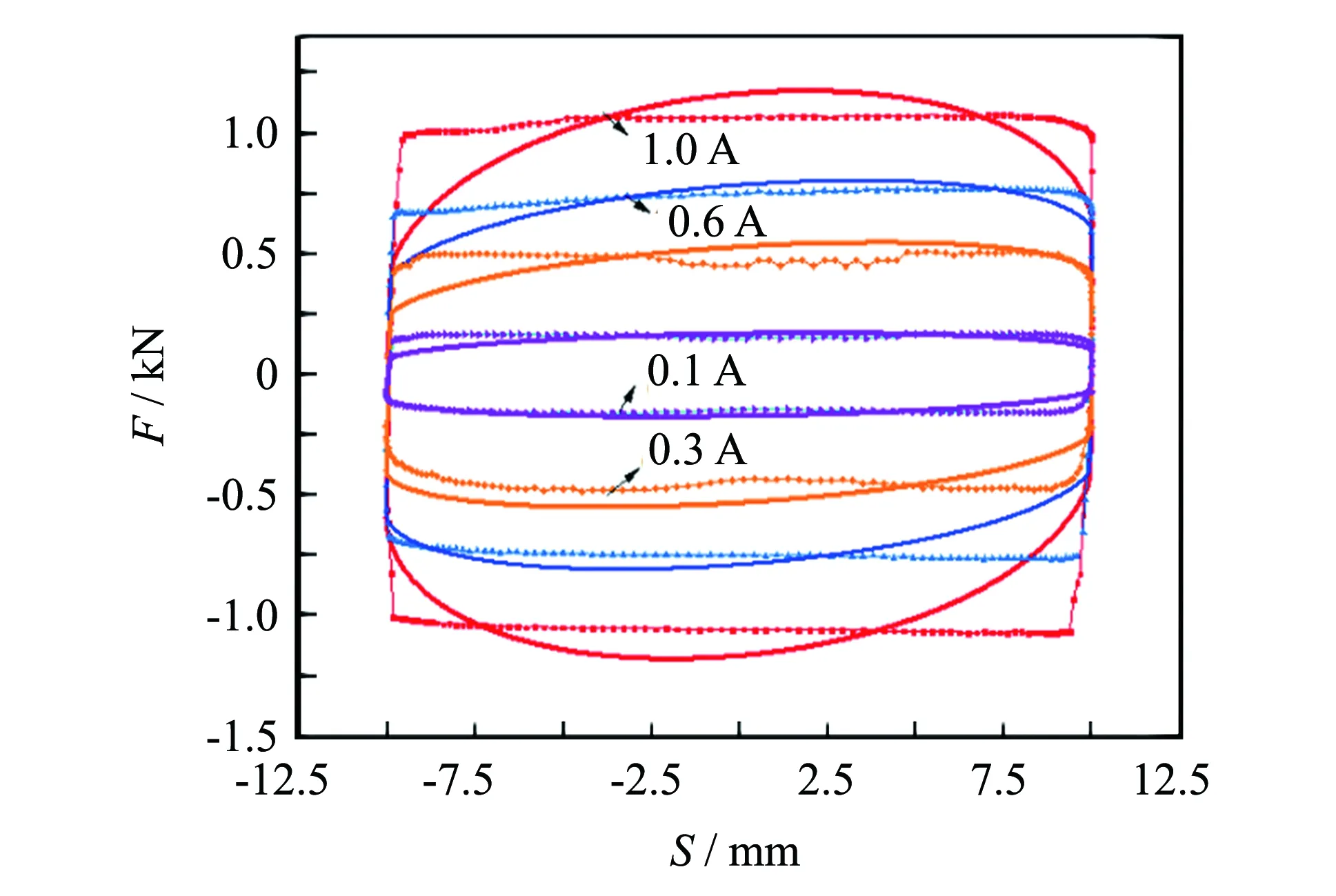
圖7 剪切閥式下阻尼器力與位移曲線Fig.7 Force and displacement curves of damper under shear valve type

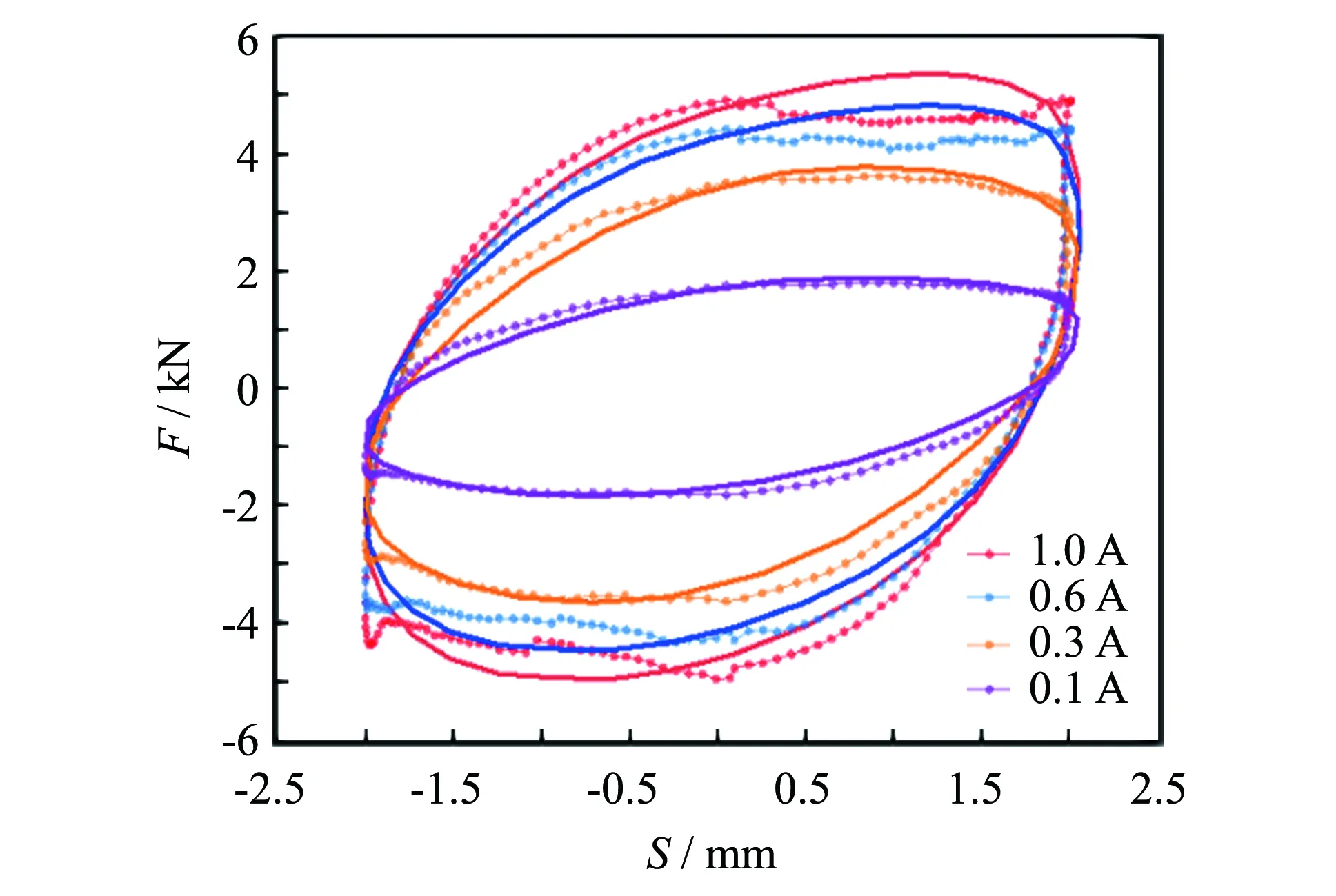
圖8 剪切閥-擠壓模式下阻尼器力與位移曲線Fig.8 Damper force and displacement curves in shear valve-squeeze mode

3 基于混合式磁流變阻尼器的機械腿模型

3.1 Simulink建模仿真

為簡化機器人運動學求解過程，給機器人加入約束條件，一般是機器人在行走過程中身軀始終保持正直狀態，而且機械腿與地面接觸時處于完全接觸狀態，減振理論模型如圖9所示.其中，機身質量為m，其振動位移為u(t) ；地面振動位移為v(t).

圖9 機械腿簡化模型Fig.9 Simplified model of mechanical leg

假設地面振動位移為：

v(t)=Asin(ωt)

(7)

式中:A為振動幅值；ω為角頻率.

建立機械腿減振系統微分方程：

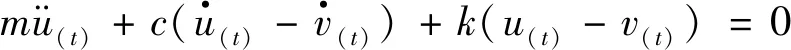
(8)

式中:c為阻尼系數；k為剛度系數；u(t)為機身位移；v(t)為地面振動位移.

機身位移為：

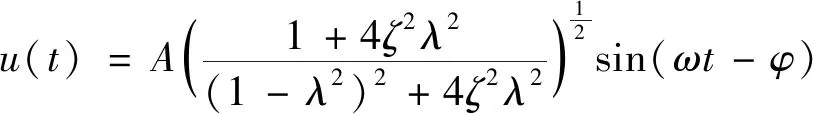
(9)

采用Simulink建立機械腿減振系統的仿真模型，在減振模型仿真過程中，減振數學模型為式(9)，具體的仿真流程如圖10所示.

圖10 機械腿仿真流程圖Fig.10 Flow chart of mechanical leg simulation

在機械腿減振系統仿真過程中，只分析給4個線圈同時通電時，混合式MRF阻尼器的減振性能將地面激勵信號設置為0～20 Hz的正弦掃頻信號.MRF阻尼器的力學模型使用自定義模塊完成，在掃頻信號下，對減振系統在固定電流作用下的振動與地面基礎振動進行仿真，得出減振系統在地面與機身的位移幅值仿真曲線如圖11所示.將Simulink仿真結果進行處理并與理論對比，得出在不同頻率下傳遞率的變化曲線如圖12所示，圖中結果表明理論推導與軟件仿真的結果較為吻合，說明所建立的Simulink模型具有可靠性.

圖11 機械腿仿真結果圖Fig.11 Simulation results of the mechanical leg

3.2 天棚阻尼控制

天棚阻尼控制的基本原理是在簧載質量與天空慣性系之間模擬連接一個阻尼減振器，能夠有效地抑制目標的振動.天棚控制模型是一種具有理想化的模型，本研究建立的天棚控制機械腿模型如圖13所示.

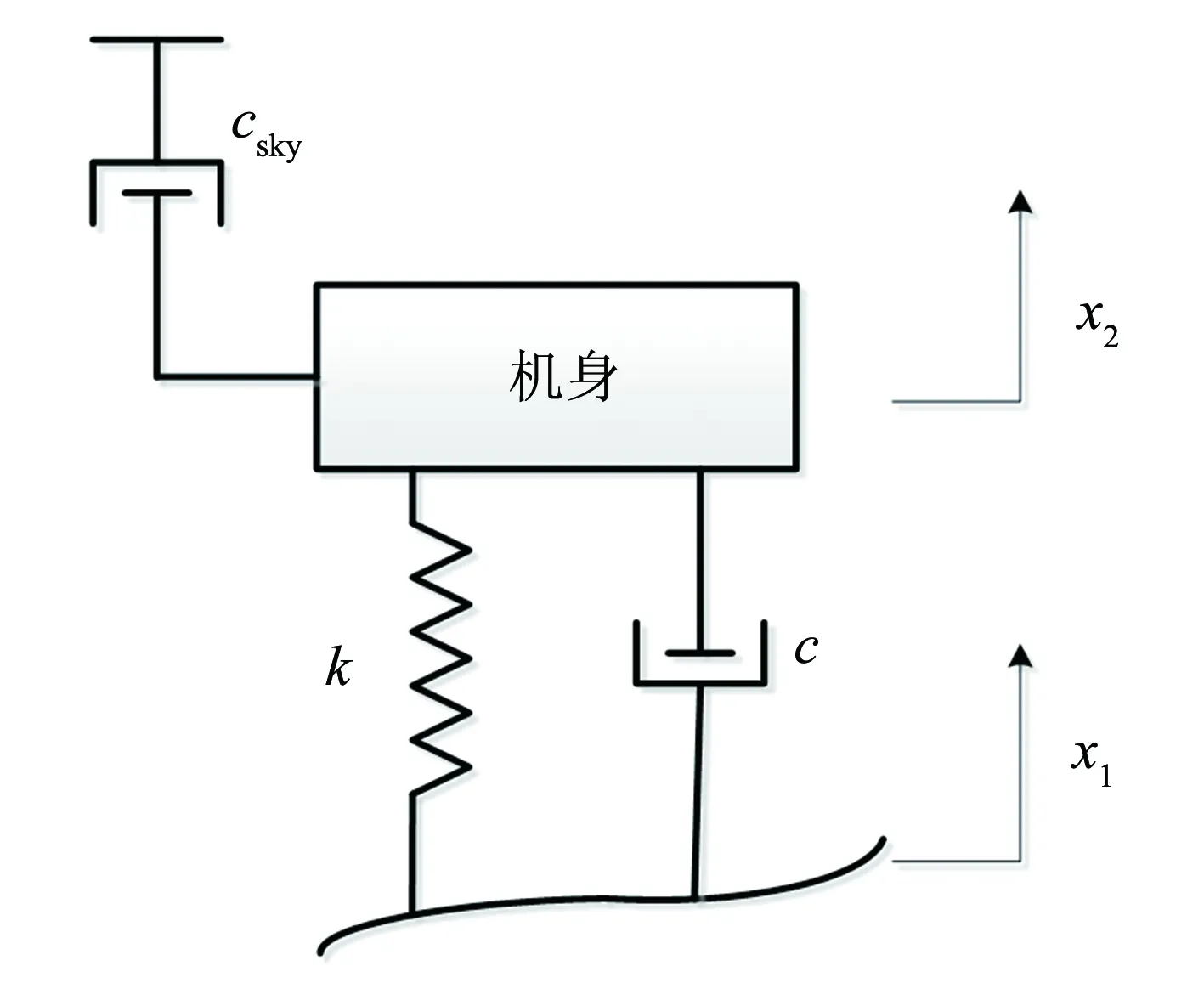
圖13 機械腿天棚控制模型Fig.13 Skyhook control model of mechanical leg

理想天棚模型時阻尼力為：

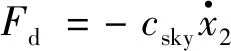
(10)

式中:csky為天棚阻尼系數.它由系統特性決定，其作用主要是調節機械腿工作來改善控制系統的平順性，其原理是將產生的天棚阻尼力與其機身運動方向相反.即：

(11)

式中:m為機身質量;x2為機身位移;k為剛度系數;c為阻尼器的粘性系數.將上式進行拉氏變換得：

ms2X2(s)+k(X2(s)-X1(s))+cs(X2(s)-X1(s))+cskysX2(s)=0

(12)

解上式方程,可得到機械腿振動的傳遞函數為：

(13)

其加速度的頻率響應函數為：

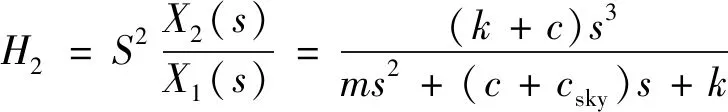
(14)

其中，由(13)、(14)式，并利用Matlab計算出機械腿天棚控制模型的幅頻響應曲線，結合仿真曲線綜合考慮取csky= 2 500 N·s·m-1.

在天棚控制系統中，磁流變阻尼器的輸出力滿足：

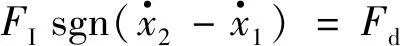
(15)

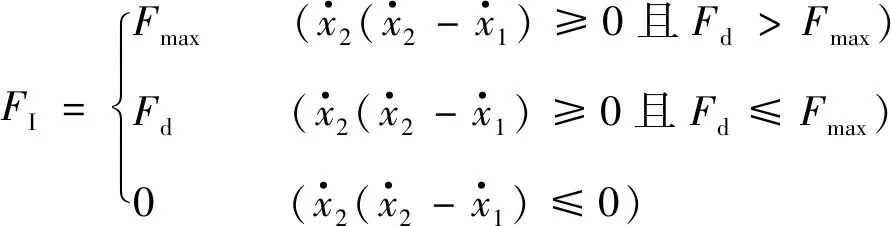
(16)

式中：Fmax為最大庫倫阻尼力.

3.3 結果分析

在機器人減振領域，一般利用簡諧信號與隨機信號來測試減振系統的好壞，隨機信號一般為白噪聲信號，采用Simulink建立天棚控制的機械腿減振系統程序，如圖14所示.

圖15和圖16是在振幅10 mm、頻率為5 Hz的正弦信號下，混合式磁流變阻尼器機械腿的減振控制仿真結果，圖17為隨機信號激勵下機械腿的減振仿真結果.從圖15和圖16可以看出，在正弦信號激勵下，天棚控制相比通入固定電流，其振動幅值從6.8 mm下降到3.3 mm，降低了49%；加速度從7.5 m·s-2下降到4.0 m·s-2，降低了47%，都有較大程度的降低.圖17結果表明,在隨機信號激勵下，機械腿振動位移也有大幅度降低，驗證了該控制算法的控制效果和實用性.

4 結語

提出一種剪切閥-擠壓混合式磁流變阻尼器對機械腿進行減振，對其力學性能進行試驗研究.基于試驗數據，選擇合適的磁流變液力學模型，利用遺傳算法對所選的力學模型進行參數辨識，并建立機械腿動力學模型.最后，在天棚控制策略下對機械腿進行了減振研究，得出如下主要結論：

1) 在混合式阻尼器實驗中，得出在剪切閥式下阻尼力最大可達1.065 kN，在剪切閥-擠壓混合模式下最大可達4.939 kN；

2) 采用遺傳算法對磁流變液的Bouc-Wen模型進行參數辨識，得到新型混合模式磁流變阻尼器的力學正模型，且模型準確；

3) 將新型混合模式磁流變阻尼器應用于機械腿減振，配合天棚控制策略，能有效抑制機械腿振動，振動位移幅值與加速度分別下降了49%和47%.