齒面點蝕對航空螺旋錐齒輪副嚙合特性影響分析

王笑樂，盧劍偉，蔡云慶，王紅州

1.安徽農業大學，安徽 合肥 230036

2.合肥工業大學，安徽 合肥 230009

螺旋錐齒輪作為一種重要的齒輪傳動零件，被廣泛地應用于航空航天和汽車等行業的傳動系統中。與直齒圓柱齒輪相比，螺旋錐齒輪常用于相交軸間的動力傳送，工作時為連續的節線接觸，具有平穩的傳遞性，噪聲和振動都非常小，適合高速傳動，因此其嚙合特性直接影響系統的傳動穩定性[1]。隨著現代航空工業對齒輪傳動要求的日趨嚴格，螺旋錐齒輪副承載工況更加惡劣復雜，服役過程中易產生齒面點蝕故障，顯著影響裝備的動力性、經濟性、平順性和可靠性[2]。而且，航空器在加工制造方面具有更高的精密性，一旦發生點蝕情況，則對其傳動系統的工作產生重要影響，甚至引起航空航天事故的發生[3]。因此，深入研究齒面點蝕對螺旋錐齒輪副嚙合特性的影響在航空航天領域具有重要意義[4]。

螺旋錐齒輪相比圓柱齒輪具有更為復雜的幾何特征和齒面形貌，點蝕的產生進一步加劇了接觸分析的復雜程度，有限元法是目前研究其故障狀態下嚙合特性的主要技術手段[5-6]。馬鵬程、汪中厚等基于Abaqus軟件研究了齒面橢球形點蝕對弧齒錐齒輪副承載傳動誤差的影響規律[7]。李秋澤等以高速動車組弧齒錐齒輪疲勞點蝕為研究對象，統計了點蝕故障的發生位置，并基于加載嚙合試驗分析了齒面接觸應力與接觸面積的變化規律[8]。馮松等對比研究了齒面磨損、微點蝕和宏觀點蝕對漸開線直齒圓柱齒輪副嚙合剛度的影響[9]。王曉鵬建立了齒面微點蝕狀態下的法向接觸剛度預估模型，計算了漸開線齒輪副不同程度點蝕狀態下的法向接觸剛度[10]。趙鑫等利用勢能法計算了漸開線直齒輪副齒面橢圓形點蝕故障下的嚙合剛度[11]。羅棚等運用Abaqus軟件建立了直齒圓柱齒輪副嚙合模型，分別獲得了健康齒、圓點蝕和方形點蝕故障齒的最大接觸應力，并基于試驗研究了不同點蝕程度對齒輪系統振動噪聲的影響規律[12]。

現階段，分析齒面點蝕對螺旋錐齒輪副嚙合特性影響規律的研究仍較少見。為此，本文以刀傾半展成法加工的螺旋錐齒輪副為研究對象，基于承載接觸分析技術（LTCA）研究了不同載荷下不同位置點蝕對齒輪副嚙合印痕、動態傳動誤差、接觸應力等嚙合特性的影響規律，為后續研究航空航天飛行器傳動系統的工作原理及可靠性分析奠定基礎。

1 螺旋錐齒輪副承載分析模型

1.1 螺旋錐齒輪副參數及實體模型

本文所研究的某航空減速器螺旋錐齒輪副采用小輪下偏置，幾何參數見表1。其中，大輪采用成形法、小輪采用刀傾法加工，是國內外航空航天專用螺旋錐齒輪副常見加工方式，大小輪的加工參數見表2、表3。

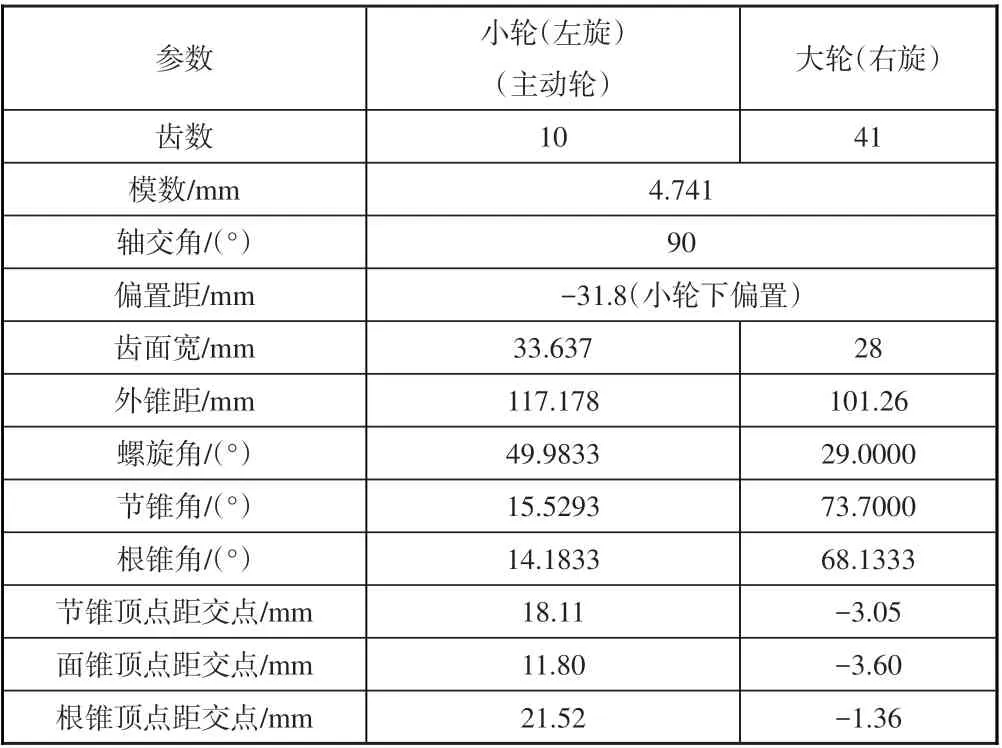
表1 螺旋錐齒輪副幾何參數Table 1 Geometric parameters of the hypoid gear pair

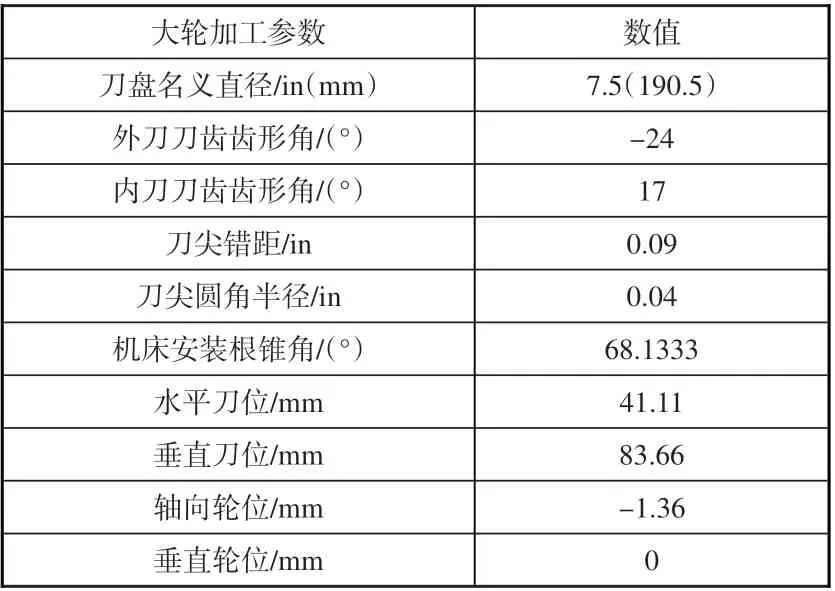
表2 大輪加工參數Table 2 Processing parameters of the gear

表3 小輪加工參數Table 3 Processing parameters of the pinion

研究螺旋錐齒輪加工過程的數學表達，基于Matlab 軟件建立機床加工過程的仿真數學模型，計算加工參數，完成虛擬加工，根據加工程序計算完成螺旋錐齒輪副含齒根過渡曲面的全齒面精確建模，求解得到大、小輪齒面點云坐標[13]。加工仿真非本文研究重點，故不再贅述。將獲得的離散點云采用曲面擬合的方式生成含齒根過渡曲面大、小輪齒面，分別建立其三維模型，如圖1、圖2所示。

圖1 大輪三維模型Fig.1 3D model of the gear

圖2 小輪三維模型Fig.2 3D model of the pinion

1.2 螺旋錐齒輪副有限元模型

將大小輪三維模型導入Hypermesh 軟件進行網格劃分，綜合考慮計算精度及效率，建立小輪全齒、大輪6 齒網格模型，如圖3、圖4 所示。為了在齒輪表面準確構造出點蝕特征，對工作齒面進行網格細化加密，控制單元長度小于0.2mm、單元厚度小于0.1mm，小輪工作齒面網格細節如圖5所示。

圖3 大輪有限元網格模型Fig.3 Finite element mesh model of the gear

圖4 小輪有限元網格模型Fig.4 Finite element mesh model of the pinion

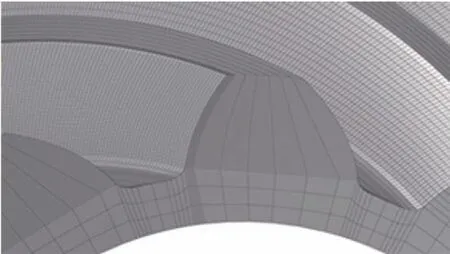
圖5 小輪工作齒面網格模型Fig.5 Finite element mesh model of the working surface of the pinion

將大、小輪網格模型導入有限元分析軟件Abaqus，完成分析類型、材料屬性、截面屬性、分析步、場輸出變量、歷史輸出變量、相互作用、邊界條件及載荷等參數設置[14]，材料參數采用45鋼參數，部分前處理參數設置見表4。

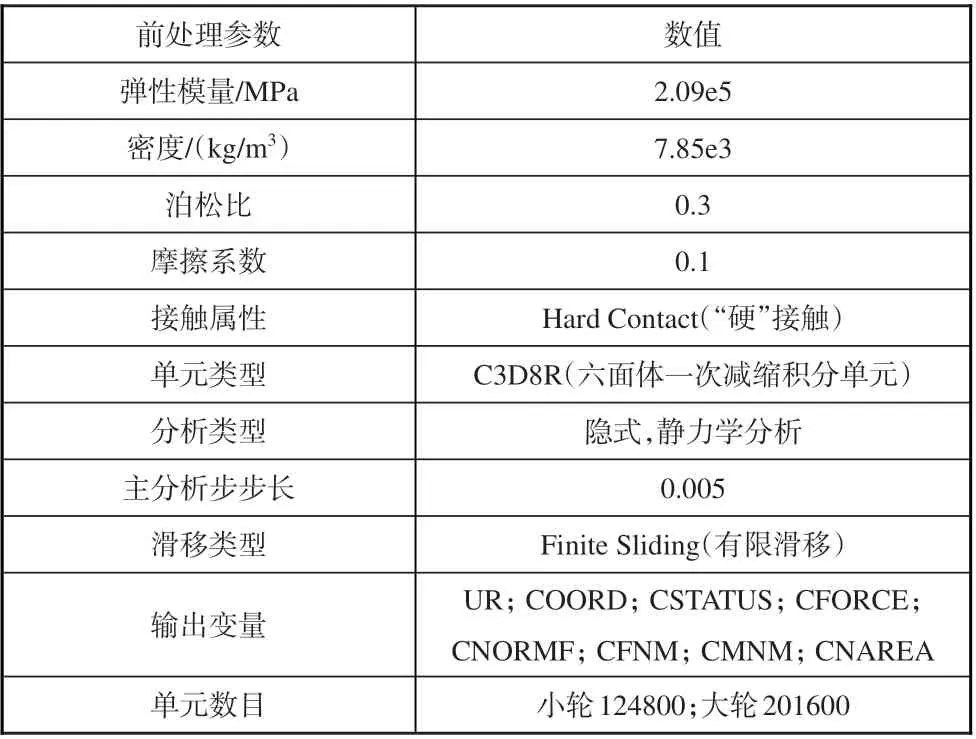
表4 部分前處理參數Table 4 Some preprocessing parameters

對螺旋錐齒輪副嚙合過程進行仿真，要模擬大輪和小輪在靜止不動時相互接觸產生的嚙合特性，由于齒側間隙的存在，齒輪剛開始接觸時可能存在嚙合沖擊現象。為使嚙合沖擊最小，迭代過程收斂，靜態分析步選擇staticgeneral 類型[15]，一般分為三個分析步，分別設置為：（1）約束小輪6個方向的自由度，將大輪繞軸線偏轉微小角度，使大、小輪齒面接觸。第(1)步設置時長為0.05s，初始增量步長設置為0.01，最大增量步長為0.05，最小增量步長為默認設置，最大增量步數設置為100。（2）釋放小輪軸向自由度，固定大輪6個方向的自由度，將小輪繞軸線偏轉微小角度，使大、小輪齒面接觸，達到初始分析狀態。第(2)步中步長相關設置同第(1)步。（3）同時釋放大、小輪軸向自由度，小輪施加繞軸線固定角速度作為主動輪，大輪則作為從動輪，完成嚙合。第(3)步根據小輪角速度及旋轉角度，設定時間為0.85s，此時嚙合至第6個齒，同時將初始增量步和最大增量步均設置為0.005，最大增量步數設置為1000。

2 螺旋錐齒輪副承載嚙合分析

2.1 健康齒輪副嚙合特性分析

分別為大輪施加100N?m、500N?m、1000N?m和3000N?m的4 種負載扭矩，為小輪添加大小為5rad/s 的驅動轉速。經Abaqus軟件仿真嚙合過程，得到4種工況下健康齒面的嚙合印痕，如圖6所示，對比發現，隨著載荷的增大，嚙合區域的面積也不斷增加，并向著兩端和齒根擴展[16]。

圖6 不同載荷下大輪齒面嚙合印痕Fig.6 Meshing pattern on gear tooth surface under different loads

對比4種工況下齒輪副嚙合至同一轉角時的等效應力云圖，如圖7 所示，隨著載荷增加，齒面應力集中區域向兩端和齒根擴展，與嚙合區域的變化特征一致，接觸區域為扁平的橢圓形，應力最大區域位于橢圓中心。

圖7 不同載荷下大輪齒面等效應力云圖Fig.7 Meshing pattern on gear tooth surface under different loads

提取不同載荷工況下第四對嚙合齒的齒面接觸力，如圖8所示。可以看出，螺旋錐齒輪齒面嚙合力曲線近似于拋物線形狀，且隨著載荷的增加，齒面嚙合力也相應增大。

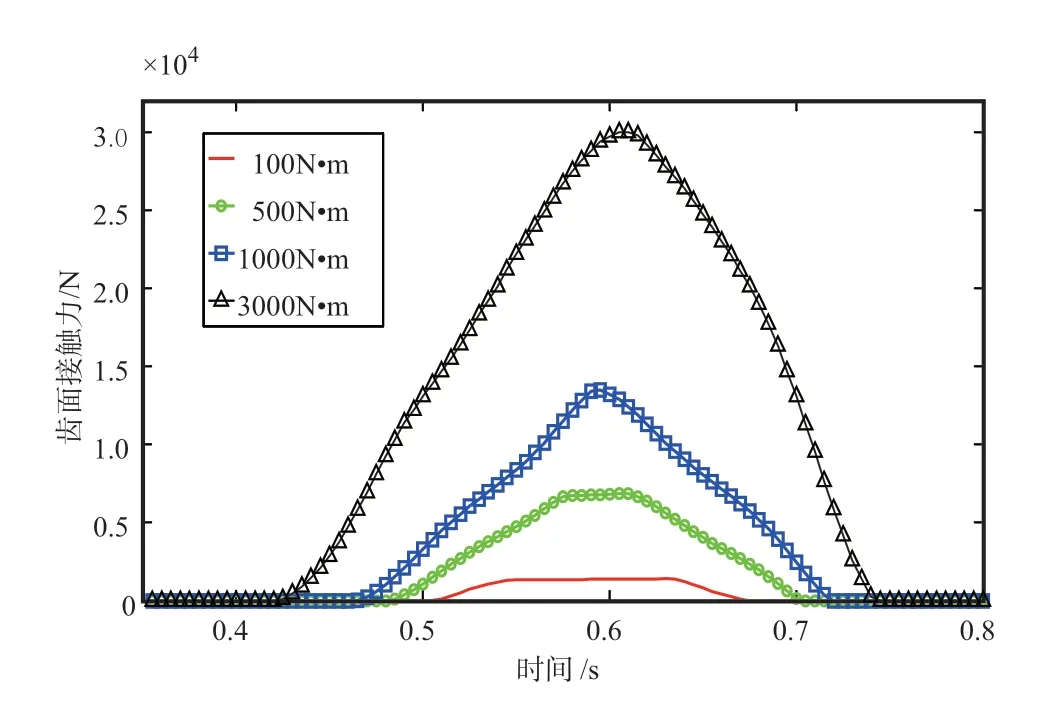
圖8 不同載荷下齒面嚙合力Fig.8 Meshing force under different loads

在理想狀態下，螺旋錐齒輪副的嚙合傳動是無誤差的，但是實際中螺旋錐齒輪副瞬時傳動比是不斷變化的，因此存在傳動誤差。傳動誤差的定義為：當小輪轉過一定角度時，大輪實際轉角與理論轉角之差。即

式中：δ為傳動誤差，Δφh1為小輪轉角，Δφh2為大輪轉角，z1為小輪齒數，z2為大輪齒數。

圖9 為齒輪副在不同載荷下的齒輪傳動誤差，可以看出，不同載荷工況下的傳動誤差呈周期性波動，隨著載荷的增加，傳動誤差幅值也逐漸增大。

圖9 不同載荷下齒輪副傳動誤差Fig.9 Transmission error of the gear pair under different load

2.2 點蝕齒輪副嚙合特性分析

本文研究的螺旋錐齒輪副小輪為主動輪，大輪為從動輪，齒數比為Z1/Z2 = 10/41，工作過程中小輪齒面嚙合次數更多，更易發生磨損失效等情況，此外小輪凹面為工作面，相同載荷下凹面應力遠大于凸面應力[17]，因此本文將點蝕模擬在小輪凹面。將大、小輪均劃分為純六面體網格，將齒面網格加密為4 層。根據500N?m 載荷工況下的齒面實際嚙合區域，分別在A、B、C 三個位置進行模擬點蝕，如圖10所示。

圖10 齒面三種點蝕位置Fig.10 Three kinds position of pitting on tooth surface

以500N?m工況為例，對比點蝕齒輪副與健康齒輪副在點蝕位置時的等效應力云圖，如圖11 所示。對比發現，由于點蝕的存在，當齒輪嚙合至該位置時，點蝕坑周圍區域的等效應力顯著增大，這將會導致點蝕面積進一步增大，從而加劇齒輪振動，對齒輪傳動誤差造成影響。

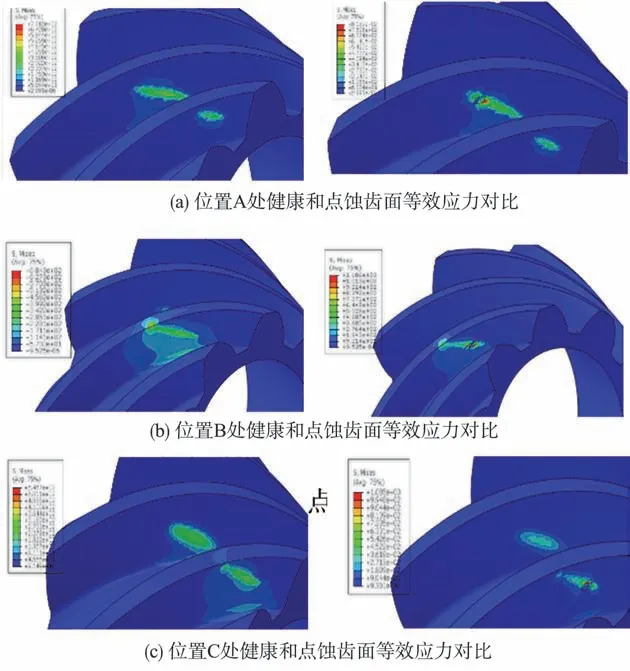
圖11 健康和點蝕齒面接觸應力對比Fig.11 Three kinds position of pitting on tooth surface

在500N?m載荷工況下，健康齒輪副與不同位置點蝕齒輪副第四對嚙合齒嚙合力變化如圖12所示。可以看出，點蝕齒輪副與健康齒輪副齒面嚙合力的變化趨勢基本一致，呈拋物線形狀。當齒輪嚙合至點蝕位置時，相較于健康齒輪，不同位置點蝕齒輪副的齒面接觸力均有不同程度的下降[18]。

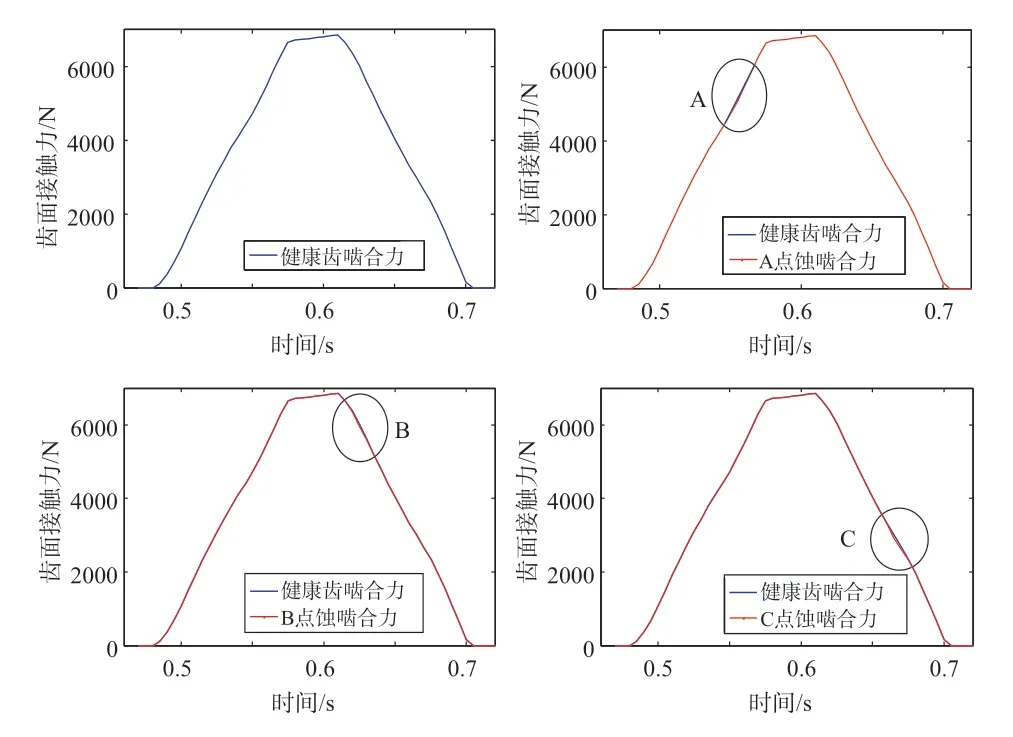
圖12 健康、點蝕齒輪副齒面嚙合力Fig.12 Meshing force on tooth surface of healthy and pitting gear pair

圖13為500N?m工況下不同位置點蝕齒輪副的傳動誤差曲線，可以看出，對于A、B、C三種點蝕位置，當齒面嚙合至點蝕區域時，傳動誤差幅值均有所增大。將健康齒輪副傳動誤差與點蝕齒輪副傳動誤差進行求差，得到圖14所示的誤差曲線。

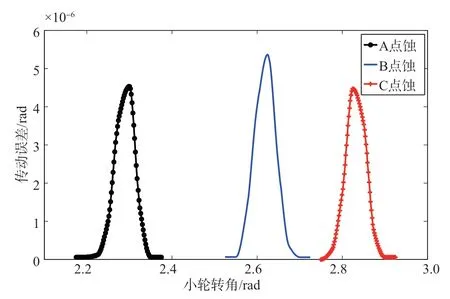
圖13 不同位置點蝕齒輪副傳動誤差Fig.13 Transmission error of the gear pair at different pitting positions

從圖14 中可以看出，相同載荷下，位于嚙合區域中心位置的B 點蝕對傳動誤差的影響較大，位于嚙合區域邊緣位置的A、C點蝕影響較小，原因是當齒面嚙合至B位置時，該區域為主要受力區，齒面應力相比較A、C區域更大，因此該位置點蝕對傳動誤差影響也較大，A、C 位置位于嚙合邊緣區域，此時有其他齒面分擔載荷，點蝕位置的應力也相對較小，該位置的點蝕對傳動誤差影響較小，因此點蝕越靠近嚙合邊緣區域，對傳動誤差的影響越小。

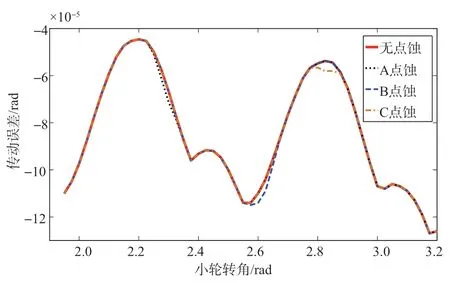
圖14 不同位置點蝕對傳動誤差的影響Fig.14 Influence of pitting at different positions on transmission error

為了深入分析不同載荷下點蝕對傳動誤差的影響，增加載荷數目，對齒輪副分別施加100N?m、300N?m、500N?m、1000N?m、3000N?m 和4000N?m 載荷，將不同載荷下的健康齒輪副傳動誤差與有點蝕傳動誤差求差，得到結果如圖15所示。

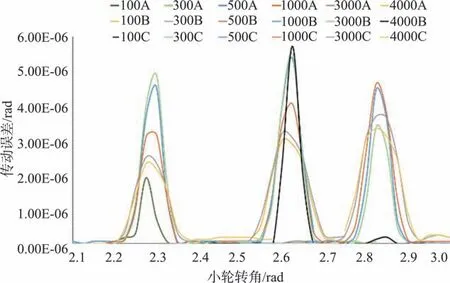
圖15 不同位置點蝕齒輪副在不同載荷下傳動誤差Fig.15 Transmission error of pitting gear pairs in different positions under different loads

圖15 中從左到右分別為A、B、C 三個點蝕位置的不同載荷對傳動誤差的影響曲線。可以看出，隨著載荷增加，靠近齒面邊緣的A、C點蝕處的傳動誤差呈先增大后減小的趨勢，位于齒面中部的B 點蝕處的傳動誤差則一直增大。原因是嚙合區隨載荷增加向齒面邊緣延伸，B 點蝕位于齒面中部，受接觸區擴大的影響不大，傳動誤差增加主要受載荷增大引起。A、C 點蝕在低載荷時位于齒面邊緣區域，但由于嚙合區隨載荷增加向兩端延伸，A、C 點蝕逐漸向嚙合區中心移動。對于A、C位置點蝕，在載荷增加前期載荷變化對傳動誤差的影響大于點蝕相對位置變化的影響，故在前期載荷增大時A、C影響曲線呈現增大的趨勢，后期隨著載荷的增大，A、C逐漸移向嚙合區域中心位置，此時載荷變化對傳動誤差的影響小于相對位置移動造成的影響，故傳動誤差隨著載荷的增大而逐漸減小。雖然載荷增大的后期點蝕對齒輪副傳動誤差的影響越來越小，但點蝕坑附近區域等效應力顯著增大，甚至有可能超過齒輪許用應力，導致點蝕坑面積擴大，甚至發展到輪齒斷裂的后果。

3 結論

本文以采用刀傾半展成法加工的螺旋錐齒輪副為對象，通過建立健康齒輪副和點蝕齒輪副的有限元模型，基于承載接觸分析技術研究了不同位置齒面點蝕在不同工況下對螺旋錐齒輪副動態嚙合特性的影響，獲得以下結論：

（1）對于健康螺旋錐齒輪副，隨載荷增加，齒面嚙合區面積不斷增大，接觸區域及齒面應力集中區向兩端和齒根擴展，傳動誤差幅值逐漸增大。

（2）螺旋錐齒輪副嚙合至點蝕位置時，點蝕處附近區域應力顯著增大，而點蝕位置齒面接觸力相比較健康齒面有所下降，會造成點蝕位置區域面積不斷增大，加劇齒輪振動。

（3）螺旋錐齒輪副嚙合至點蝕位置時，傳動誤差絕對值有所增加，位于齒面中部位置的點蝕對傳動誤差影響較大，位于邊緣區域的點蝕對傳動誤差影響較小。當點蝕位于齒面中部時，載荷越大，點蝕對傳動誤差的影響越小，但影響范圍越廣。

（4）將螺旋錐齒輪應用至航空航天領域時，應采取一定的手段避免點蝕情況的發生；一旦航空減速器中螺旋錐齒輪副發生點蝕，應及時采取補救措施或者更換相應零件，以便降低事故發生的概率，提升航天器性能的可靠性。