求解SDCP 模型問題的人工蜂群算法研究*

牛佳惠 肖 寧 王煜東

（1.陜西職業技術學院人工智能學院 西安 710100）（2.國網咸陽供電公司 咸陽 712100）

1 引言

隨 機 相 關 機 會 規 劃［1～2］（Stochastic Dependent-Chance Programming，SDCP）是隨機規劃的一個子模型，是在隨機環境下，決策者以極大化隨機事件成立的機會（概率）為目標而提供最佳策略的一個不確定模型。如何高效求解SDCP 模型問題，一直是存在于經濟、管理、最優控制等領域中的熱點研究方向。

在實際的含有隨機不確定因素的水土資源的最優配置、電力系統優化、無線傳感網絡的路由選擇、作業車間調度、路徑優化等應用方向中，SDCP問題不難提取，而SDCP 問題所表現的隨機性及非線性導致了它難以求解，因而，研究者仍在繼續探究著SDCP 這類問題的更優的求解途徑。現在，各類智能計算技術在高速發展的算力平臺的助力下，可以計算常規的或傳統的方法很難實現的繁雜問題。SDCP問題的有代表性求解算法是基于遺傳算法（Genetic Algorithm，GA）［1～3］，但因該算法自身的一些缺點，如，遺傳操作過程復雜、程序需要控制的變量多、計算耗時、計算量大及容易早熟等等，探究更為有效的SDCP模型問題的求解途徑仍舊為研究人員的關注點。

2005 年，Karaboga 提出人工蜂群（Artificial Bee Colony，ABC）［4］算法，為蟻群算法、微粒群算法之后的又一種仿生智能算法，如今已是智能計算的一個重要組成部分，同微粒群算法、遺傳算法等群體智能算法相比較，它具有參數少、結構簡單、易實現，并在整個尋優階段，局部、全局搜索在每次迭代中都會進行，這一特點提高了該算法獲得最優解的概率，這在很大程度上阻擾了發生早熟等優點，從算法的提出到如今的不足十五年，ABC算法在最優控制等領域中的應用得到大量的研究者的研究和關注［5～15］，然而，至今國內外文獻資料只有本文作者發表的有關蜂群算法在隨機規劃問題求解中的應用研究的論文［16］，本文就是把隨機模擬技術和人工蜂群算法相融合求解隨機規劃中的SDCP 模型問題，本論文算法的優化效果通過代表性的算例加以檢驗，同時它也為其它不確定環境下尋優提供了思路。

2 SDCP模型

SDCP單目標模型形式如下：

式中：ξ，x分別代表隨機向量和決策向量，f（x）=pr｛hk(x,ξ)≤0,k=1,2,…,q｝，不等式組：hk(x,ξ)≤0,k=1,2,…,q是對隨機規劃的目標事件的描述，gj(x,ξ)≤0,j=1,2,…,p代表了隨機不確定環境。該模型描述了在隨機環境gj(x,ξ)≤0,j=1,2,…,p約束下使得事件hk(x,ξ)≤0,k=1,2,…,q成立的機會達到最大。在隨機環境下，一個事件的機會等于與該隨機事件相容的概率，這就是不確定原理所描述的內容，它是求解SDCP 的理論基礎。

在管理目標與部分優先結構給定后，可通過極小化與本目標的正或負偏差，獲得FDCP 目標規劃描述如下：

這里，gj描述了隨機環境中的約束函數；pj描述了優先系數，代表各個目標的相對重要性，且對于?j，有pj?pj+1；第i個目標小于、大于目標值的偏差用代表；目標約束的數量用m 代表；p 代表系統約束的數量；1 代表了優先級的數量；目標i 的函數值由bi代表；hik代表了實值函數；uij、vij分別描述了目標i的第j個優先級的正、負偏差權重系數。

3 人工蜂群算法

2005 年，Karaboga 提出人工蜂群算法，它也是基于仿生智能的一種啟發式算法，該算法受啟于蜂群的協作覓食，不斷探索蜜源的行為，以找到花蜜量最大的蜜源為目標，完成優化問題的求解。

在該算法中，整個蜂群由三類角色的蜜蜂組成：雇傭蜂、偵察蜂和觀察蜂，它們在覓食中分工合作，不斷迭代，其中，雇傭蜂的數量是整個蜂群的二分之一，同具體的蜜源相對應，雇傭蜂以跳搖擺舞的形式來與其他的個體分享蜜源信息，觀察蜂數量上也是占蜂群總數的二分之一，它們等候于舞蹈區，通過分享雇傭蜂的信息對蜜源完成挑選，雇傭蜂們總能根據自己記憶中的最優位置并在其周圍進行探測與偵查，丟棄食物源變為偵察蜂的雇傭蜂的工作則是開始在蜂房周圍隨機地探索新食物源。

在ABC 算法中，最優化問題的求解就是在問題空間上不斷搜尋最優的數據使得目標函數達到最優。在維數為D的問題空間，食物源的位置對應了優化問題的候選解，蜜源的濃度則代表了每個候選解的適應度，食物源的數目等于雇傭蜂和觀察蜂數目的和，表示為CN，若第i 個食物源的第n 次迭代的位置表示為xi=[xi1,xi2,…xiD]，則該食物源i的初始位置利用式（1）在搜索空間隨機產生：

雇傭蜂根據式（2）在當前位置周圍探測與偵查潛在食物源：

其中的k（k≠i）代表在蜜源里隨機選擇一個蜜源k；若新的蜜源new_的適應度好于，那么通過貪婪機制選擇保留該較好解。所有的雇傭蜂完成了式（2）的運算之后，則將蜜源信息帶回蜂巢并通過舞蹈的方式進行分享。觀察蜂依據雇傭蜂所分享的花蜜信息，依照式（3）選擇一個蜜源：

其中，fiti表示第i 個潛在解的適應度值，pi則代表了食物源i被選中的概率。

以尋找最小化問題為例，潛在解的適應度值依據式（4）完成：

其中，fi代表了第i個潛在解所對應的函數值。

所有的雇傭蜂和觀察蜂全部完成了搜索，然而食物源相對應的適應值在預定的number 次搜索，并在限定的食物源的改進次數limit 次仍沒取得更好的食物源，則說明該潛在解已經淪為了局部最優解，則該食物源被丟棄，而與該食物源所對應的雇傭蜂轉變角色成為偵察蜂，它將依據式（5）繼續搜索新的食物源。

綜上，使用ABC 算法尋優的要點是雇傭蜂的任務是負責搜索食物源；觀察蜂的任務是依據雇傭蜂所分享的花蜜信息，然后觀察蜂以指定的概率值完成對食物源的篩選；若某蜜源被丟棄，那么生成一個偵察蜂與隨機產生的新食物源相對應。

4 嵌入隨機模擬的ABC 算法求解SDCP模型問題

SDCP 模型問題求解時，通過使用人工蜂群算法在解空間進行尋優，在不斷地迭代時需完成求解隨機適應度值，適應度值的計算離不開隨機機會函數的計算，而利用隨機模擬技術可很容易地進行計算，在利用ABC 算法進行尋優時，它主要為算法的初始化及所有迭代中均需要隨機模擬的概率估計算法來實現花蜜量的計算。

4.1 隨機模擬的概率估計算法

常規的解析法很難計算隨機事件的機會，現通過隨機模擬求解事件的機會。

已知量ξi（i=1，2…m）隨機變的概率分布函數用?i（i=1，2…m）表示，X 代表給定的決策向量，則計算隨機事件的機會如下：

下面給出隨機模擬的概率估計算法的基本流程：

步驟1：N′=0；

步驟2：利用概率分布函數?i，生成隨機變量ξi；

步驟3：若果hk（x，ξ）≤0 ，gj（x，ξ）≤0 ，則，N′++；

步驟4：步驟2～步驟3 共重復執行N次；

步驟5：將N′/N的值返回。

4.2 算法步驟

嵌入隨機模擬的ABC 算法求解SDCP 算法的操作步驟。

步驟1：在D 維問題空間中對蜜源總數為ColonyTotal 的蜜源xi（i=1，2…ColonyTotal）初始化：雇傭蜂、觀察蜂的數目均為蜜源數量的ColonyTotal/2，蜜源最大限制搜索的次數limit，最大迭代次數MaxLoopNumber，各個維度的上、下界，通過式（1）獲得ColonyTotal個隨機初始蜜源，并將雇傭蜂與其相對應，利用隨機模擬概率估計算法計算適應度值，并對雇傭蜂位置、觀察蜂位置、最好蜜源等初始化。

步驟2：雇傭蜂通過式（2）修改食物源信息，通過隨機模擬概率估計算法計算給定的隨機機會函數的值并計算適應度值。然后對新食物源實施評價：若新食物源：new_的適應度比的適應度更好，那么通過貪婪機制把目前的較好解進行保留，反之則保留。

步驟3：利用式（3）來獲得雇傭蜂找到食物源被觀察蜂追隨的概率，然后觀察蜂則依據該數值來挑選食物源。

步驟4：使用與雇傭蜂相同的搜索方式，觀察蜂進行食物源的搜索，也就是通過隨機模擬可信性估計算法計算機會函數值、花蜜量，再通過貪婪機制保留當前最好的食物源。

步驟5：檢驗各食物源的連續搜索記錄即number 的值是否超過最大限制次數limit，如果超過，那么通過式（5）隨機產生一個新的食物源，利用隨機模擬概率估計算法計算隨機機會函數值、適應度值，相應的角色轉變：雇傭蜂轉變成偵察蜂，仍然通過貪婪機制保留當前最好的食物源。

步驟6：判斷此時的算法是否達到了已經給定的最高迭代次數MaxLoopNumber，若滿足，則尋優結束，否則跳轉到步驟2。

5 性能測試與效果對比

筆者借助于經典的文獻［1］里的實例完成仿真實驗。

例5.1對單目標的SDCP模型進行求解：

式中，ξ1服從正態分布N（5，1），ξ2服從指數分布EXP（4）。

例5.2對目標規劃SDCP進行計算：

式中，ξ1服從從均勻分布U［3，5］，ξ2服從正態分布N（3.5，1），ξ3服從指數分布EXP（9）。

對于例5.1，事件為x1+2x2+3x3+4x4=6，該事件ε的支撐用ε*表示，ε*=｛x1,x2,x3,x4｝，對應的相關支撐用ε**表示，ε**=｛x1,x2,x3,x4｝，根據隨機不確定原理，ε事件的機會函數：

機會函數的值可通過概率估計算法求得。

算法中相關參數的設置等同于文獻［1］：隨機模擬次數RandTime 設置為5000 次；蜂群規模ColonyTotal 設置為30 個；迭代次數MaxLoopNumber 設置為300 代；運行次數設置為1。雇傭蜂和觀察蜂的數目都設置為15 個，最大限制搜索的次數limit設置為15次。

顯然，它們的機會函數值可利用概率估計算法求得。

算法中相關參數的設置等同于文獻［1］：迭代次數MaxLoopNumber 設置為1000 代；隨機模擬次數RandTime 設置為6000 次；蜂群規模ColonyTotal設置為30 個；運行次數設置為1 次，雇傭蜂的數目設置為15個，觀察蜂的數量設置為15個，最大限制搜索的次數limit設置為15次。

在內存容量8GB、CPU 主頻3.0 GHz、操作系統Win10、Visual C++6.0為主要配置的臺式電腦上完成驗證。

在例5.1 中：嵌入隨機模擬的ABC 算法運行的結果見表1，相比于文獻［1］中的結果，本文的優化效果和利用了GA 算法的文獻［1］的相當，但從迭代過程可知，文獻［1］迭代到300 代取得了最優值94.7%，本文的ABC算法只要迭代到98代時就可達到，本文算法所得的最優值隨著迭代次數增加的變化流程，進行每間隔10 代采樣一次，迭代曲線如圖1 所示，它直觀地地展示了整個迭代過程：當迭代次數增加時，問題的全局最優值開始穩定。

圖1 實例5.1迭代曲線圖

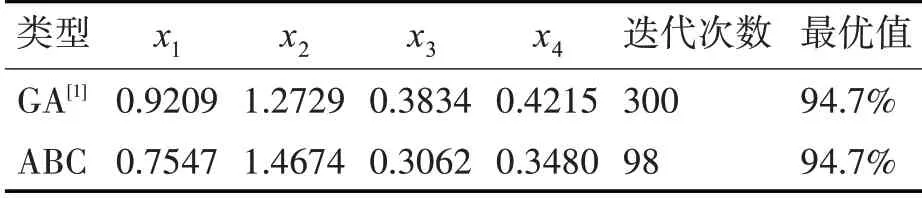
表1 實例5.1兩種算法的優化結果

在例5.2 中：運行嵌入隨機模擬的ABC 算法所得的最優解、最優值和結果如表2，同文獻［1］中的求解結果相對比，顯然優于文獻［1］：文獻［1］中第一、第二目標的負偏差、可以滿足，但第三目標的負偏差的最終優化結果為0.048，本文算法優化的效果是所獲得的最優解對應的所有目標負偏差均能滿足。

表2 實例5.2兩種算法的優化結果對比

6 結語

人工蜂群算法的策略是局部、全局搜索同時進行，這使得本算法具有了很強的全局尋優、收斂能力，本文主要討論了嵌入了隨機模擬的人工蜂群算法求解SDCP 問題，對照以GA 算法為核心的混合智能算法所得的求解結果，本算法求解質量顯著，展示了它對于SDCP問題的求解優勢。補充了通過ABC算法對隨機規劃問題求解研究的缺席，也拓展了該算法的應用研究范圍。

值得一提的是，本文作者將ABC 算法對隨機規劃的另外兩個子模型以及模糊規劃模型進行了仿真實驗，取得了與本文類似的結果，這為各類混合不確定規劃問題的求解提供了參考，這是后期我們將開展的探究。