多用戶大規模FD-MIMO 下行系統中基于降維的仿射投影解碼策略*
陳 靖,戴譚明,吳君欽
(江西理工大學,江西 贛州 341000)
0 引言
雖然有研究表明三維大規模多輸入多輸出(Full-Dimention Multiple Input Multiple Output,FD-MIMO)多用戶系統能提升傳輸效率[1-2],但實際上,由于用戶間存在干擾,必然使得系統性能降低。如果基站側和用戶側都獲取到瞬時信道狀態信息(Channel State Information,CSI),可通過臟紙編碼技術達到其最大可實現的速率域[3]。然而,一方面,臟紙編碼技術具有非常高的復雜度;另一方面,在基站側獲取瞬時CSI 難以實現。因此,利用臟紙編碼技術提高傳輸效率存在較大的挑戰性。緊接著,有限反饋預編碼碼本的設計被提出,如文獻[4]提出了基于單用戶FD-MIMO 下的窄帶和寬帶的量化策略。之后,文獻[5]基于多用戶的FD-MIMO下行系統采用了一種協同反饋方案,通過設備間相互通信的方式交換CSI,再計算預編碼器,并將預編碼器反饋給基站;然而該方案適用于用戶相隔較近的場合,且因天線規模較大,導致反饋開銷增加,同時在用戶數較多的情況下,交換時延也會增加。接著,文獻[6]基于有限反饋大規模MIMO 系統提出了內外層聯合預編碼策略。但在基站側完全不知道CSI 的場景下,無論是臟紙編碼技術,還是預編碼技術,都難以達到最大可達速率域。
本文基于基站側完全不知道CSI 的場景,針對大規模FD-MIMO 多用戶系統,首先在基站側采用降維矩陣[7-9]將大規模天線進行有效合并,其次在接收方利用仿射投影技術[10]提出新的解碼策略。由于基站側天線規模巨大,利用降維矩陣既可減少系統開銷,又能降低解碼復雜度,而且能將多根天線上的信號聯合成單個波束,有利于提升空間增益。此外,降維矩陣與CSI 是獨立無關的。因下行信道中的每一個用戶接收到的信號都涵蓋了基站發送給全部用戶的信息,由此勢必會帶來多用戶間的干擾。為了消除這些干擾,并獨立地解出各自需要的信號,提出了仿射投影解碼策略,該策略能有效地處理用戶間的干擾。與此同時,本文也提出了基于循環矩陣形式的傳送方案和解碼方法,并從理論上分析了所提出解碼策略的性能。分析結果表明,循環重復傳送信號會導致速率下降,但當用戶數與合并后的天線數相等時,仿射投影解碼策略仍能達到最佳自由度。
文中的符號定義:Cn×m表示n×m的復矩陣,分別表示取共軛、轉置和共軛轉置,分別為兩個矩陣的Kronecker積和兩個矩陣的直和。E(●)表示數學期望,CN(μ,σ2)變量服從均值為μ、方差為σ2的復高斯分布。
1 預備知識
1.1 系統模型和降維矩陣的引入
本文采用文獻[2]中的信道模型,基站側配置M=Mv×Mh根天線,其中Mv表示垂直方向上的天線數,Mh表示水平方向上的天線數,dv表示垂直方向天線間距,dh表示水平方向天線間距,K表示用戶數量。如圖1 所示。
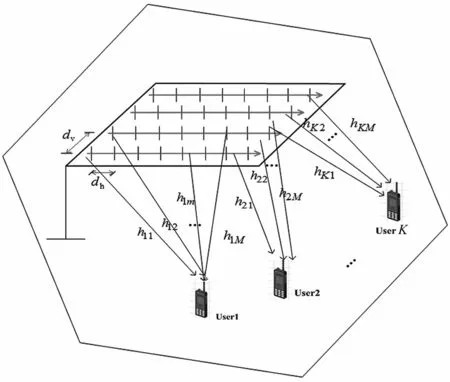
圖1 多用戶大規模FD-MIMO 下行系統
假設基站與天線間存在P個輻射路徑,且每個輻射路徑可以表示為:
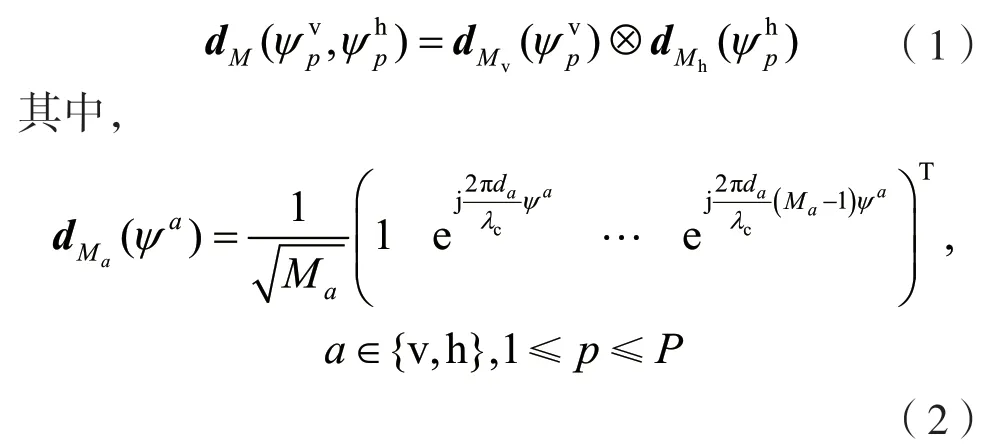
式中:ψv=sin?v;ψh=sin?hcos?v。?a是陣列向量的角度。λc是中心頻率fc所對應的波長,滿足c=fcλc,c是光速。則信道可表示為:
式中:D為輻射路徑。a=(α1…αp)T∈CP是各輻射路徑的增益,假設各路徑增益相互獨立且αp~CN(0,1)。由于系統中天線數量巨大,降維矩陣可將大規模天線進行有效合并,從而降低系統開銷。定義降維矩陣[8]:
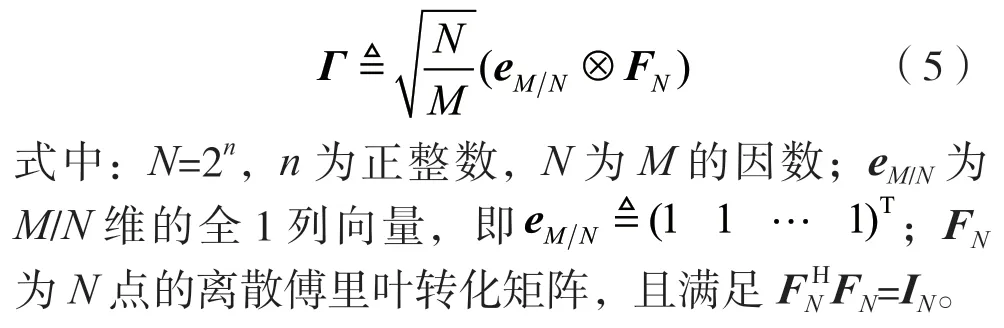
假設在該系統中,基站側的天線數為M,同時給K個單天線用戶發送信息。第i個用戶的碼本記為Φi,其功率滿足E(|sit|2)≤ρi,其中sit是碼本Φi中的碼字,ρi是第i個用戶的功率。
基站傳送信息的方案如下:
(1)根據第i個用戶的需求在對應碼本中選擇碼字sit∈Φi(t=1,2,…,T,i=1,2,…,K),T為時隙數;
(2)將步驟(1)中獲得的碼字映射到信息矩陣S∈CN×T中;
(3)最后,利用基站側的M根天線,經降維后在T時隙內,對信息矩陣S進行傳輸。
基于上述假設的信道模型,以第i個用戶的接收信號為例,則有:
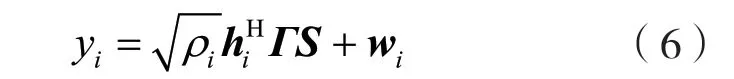
式中:hi為第i個用戶的信道;Γ為M×N維的降維矩陣;wi∈C1×T為噪聲向量,且每個分量都為均值為0、方差為1 的復高斯變量,分量間相互獨立。
1.2 仿射投影及極分解基礎
假設U,V是某個向量空間中的兩個子空間,且U∩V=?,其中,U?span{u1u2…un},{v1v2…vn},記Z=U⊕V(表示子空間U和V的直和),其中{u1u2…un}和{v1v2…vn}分別為U和V的一組基底。<,>表示兩個向量的內積,定義如下矩陣:
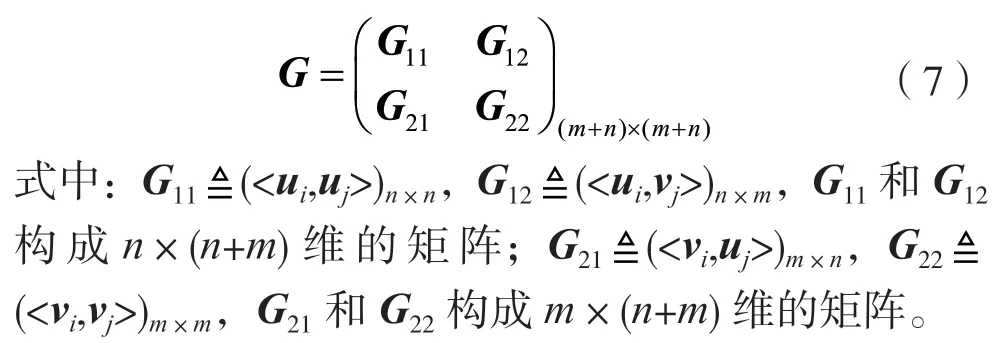
由于子空間U和V的交集為空,故這兩個空間的兩組基底必然線性無關,也就是說矩陣G11和G22可逆。此外,因空間Z=U⊕V,所以{u1u2…un,v1v2…vn}可作為Z的一組基底,因此矩陣G也是可逆的。對于任意給定的向量z∈Z,存在唯一一組分解使得z=u+v,其中(u∈U,v∈V),可通過下述方法獲得這個線性組合的系數,假設:

因矩陣G可逆,故方程兩邊左乘G-1,可得到系數的矩陣形式。
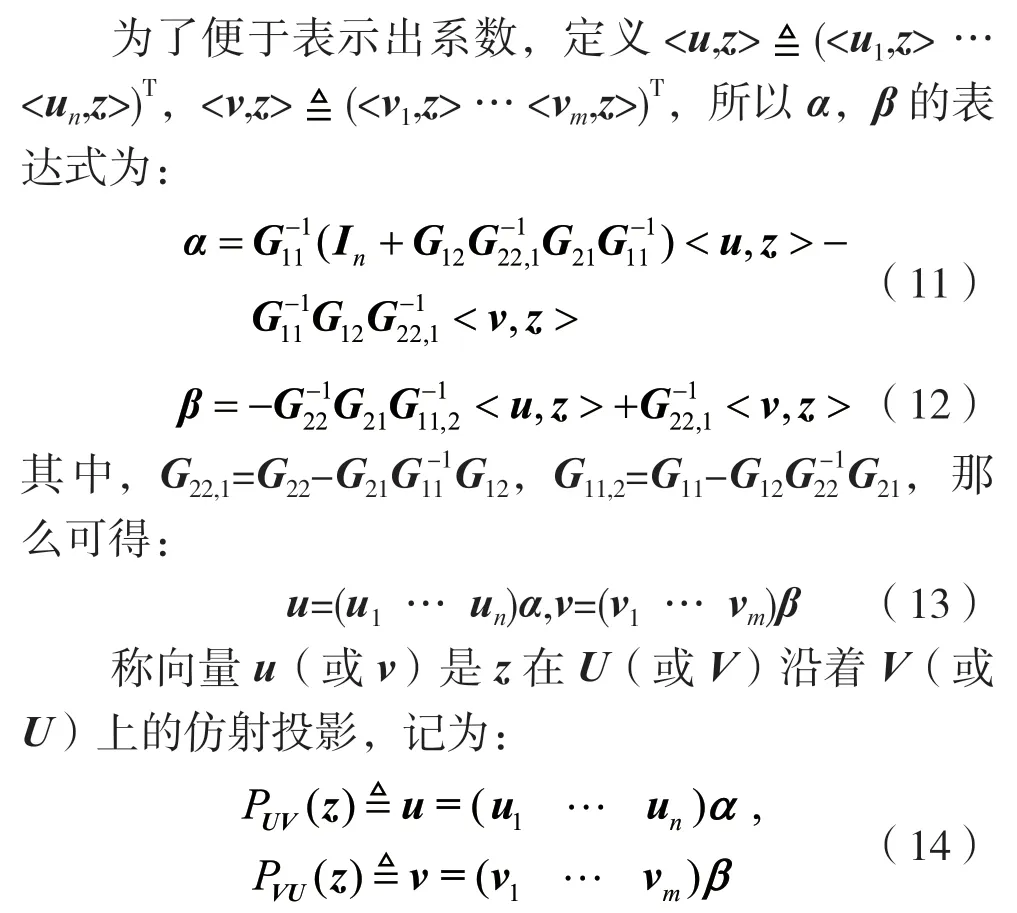
針對極分解,可給出如下定理。
設J∈Cn×m,則存在酉矩陣X和唯一的半正定矩陣W,使得:

式(15)即為矩陣J的極分解,其中,矩陣W與X分別稱為矩陣J的Hermite 因子和酉因子。矩陣的極分解是根據復數的極形式作出的,其幾何意義是先旋轉,然后再沿著一組正交的方向作伸縮。
2 傳送方案以及相應的解碼策略
2.1 基站側的傳送方案
2.1.1 傳送方案一
假設基站經合并后的天線數與用戶數的比值為g(g為整數),即g=N/K,本文提出的傳送方案的主要思想是,將全部用戶需要傳送的信號送入到傳輸矩陣S中,而不同用戶的信號放入傳輸矩陣S的不同層中。假定N=T,所以此時傳送矩陣S∈CN×N是方陣,則其第i層記為,其定義為:
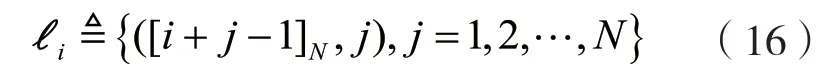
式中:[i+j-1]N表示i+j-1 對N取模運算;([i+j-1]N,j)表示傳輸矩陣S的第[i+j-1]N行第j列,在本文中稱([i+j-1]N,j)為的第j個元素。
具體的傳輸方案如下:
(1)根據第i個用戶的需求在對應碼本中選擇相應的g個信號,記為si1,si2,…,sig(i=1,2,…,K);
(2)將si1置于傳輸矩陣S第(i-1)×g+1 層的各個位置上,si2置于傳輸矩陣S第(i-1)×g+2 層的各個位置上,以此類推就可組成N×N維的信號傳輸矩陣S;
(3)利用基站側的M根天線,經降維后在T時隙內對信息矩陣S進行傳輸。
2.1.2 傳送方案二
該傳送方案假定一個用戶僅接收一個信號,其核心思想是將全部用戶的信號送入一個傳輸矩陣S′中,具體傳輸過程如下:
(1)依據K個用戶所需發送的數據信息來選擇相應的符號,記為s1,s2,…,sK;
(2)基站端在T=K=N個時隙內傳輸信號矩陣S′,傳輸信號矩陣S′的具體形式如下:
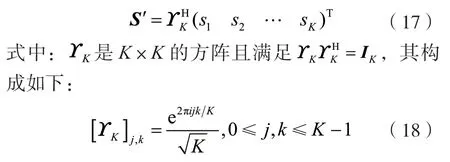
2.2 基于仿射投影的解碼策略
基于傳送方案一,以第一個用戶為例,利用仿射投影策略對用戶進行解碼,解碼過程如下文所述。這里為了便于推導,引入一個單位循環矩陣記為:
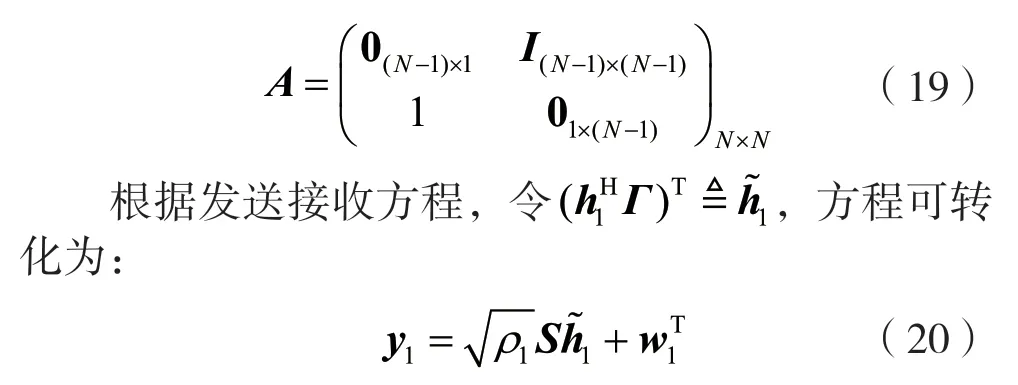
式中:y1為在N=T下第一個用戶接收到的信息。式(20)可改寫為:

通過這種方法消除了用戶間的干擾。為進一步簡化計算,可令:

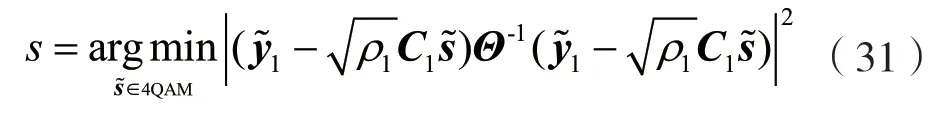
2.3 基于循環矩陣下的解碼策略
基于傳送方案二,以第一個用戶的接收信號為例,則有:

根據形式可知H為托普利茨矩陣,由文獻[11]知,可對該矩陣進行分解得到:

式中:Λ為對角矩陣,且組成元素均為H的特征值。其各個元素的形式如下:
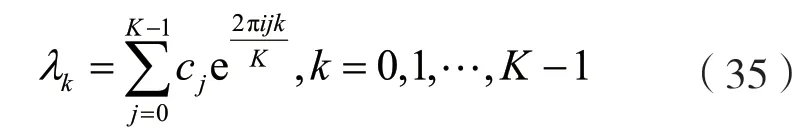
所以發送接收方程可改寫成:
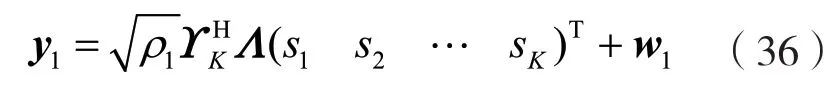
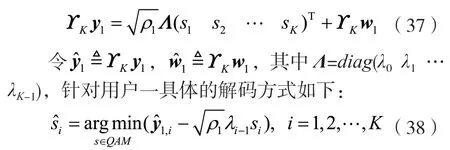
3 基于仿射投影解碼的性能分析
3.1 基于仿射投影的可達速率域分析
以用戶一為例,經降維矩陣與仿射投影相結合技術處理后,在信道確定時,在T個時隙內傳輸N次就等價于信道系數為C1的加性高斯白噪聲信道。由信道容量公式可知,記用戶一的可達速率域為R1,R1可表示為:
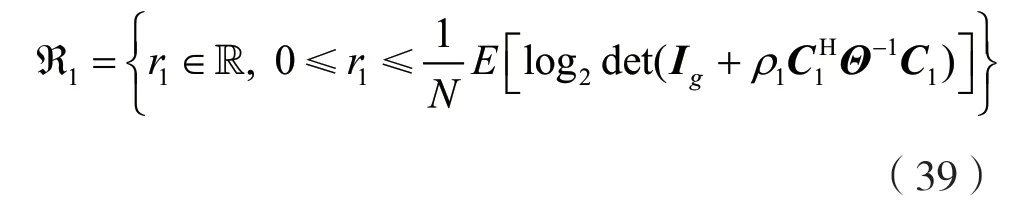

所以,R1也可表示為:

3.2 基于仿射投影的自由度分析
基于多用戶FD-MIMO 的下行系統,本文采用的降維矩陣與仿射投影相結合的解碼策略,這里考察其可達自由度,由文獻[12]可知,記該自由度為:
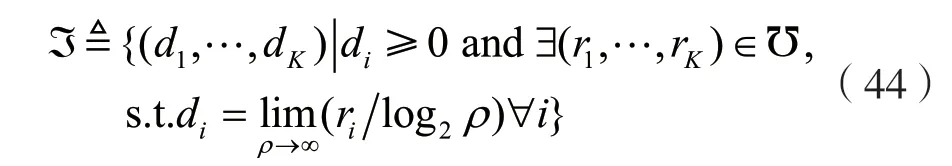
式中:? 為系統的容量域。
系統的最大自由度記為:
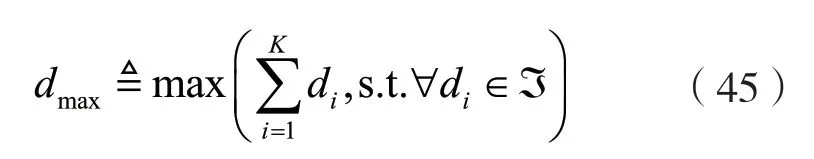
由文獻[10]可知:
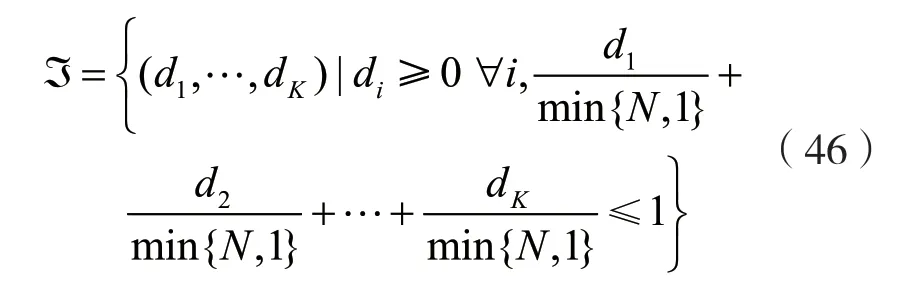
由于N>1,所以可得:
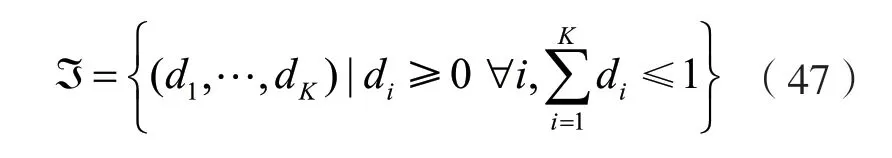
所以可推出dmax≤1。
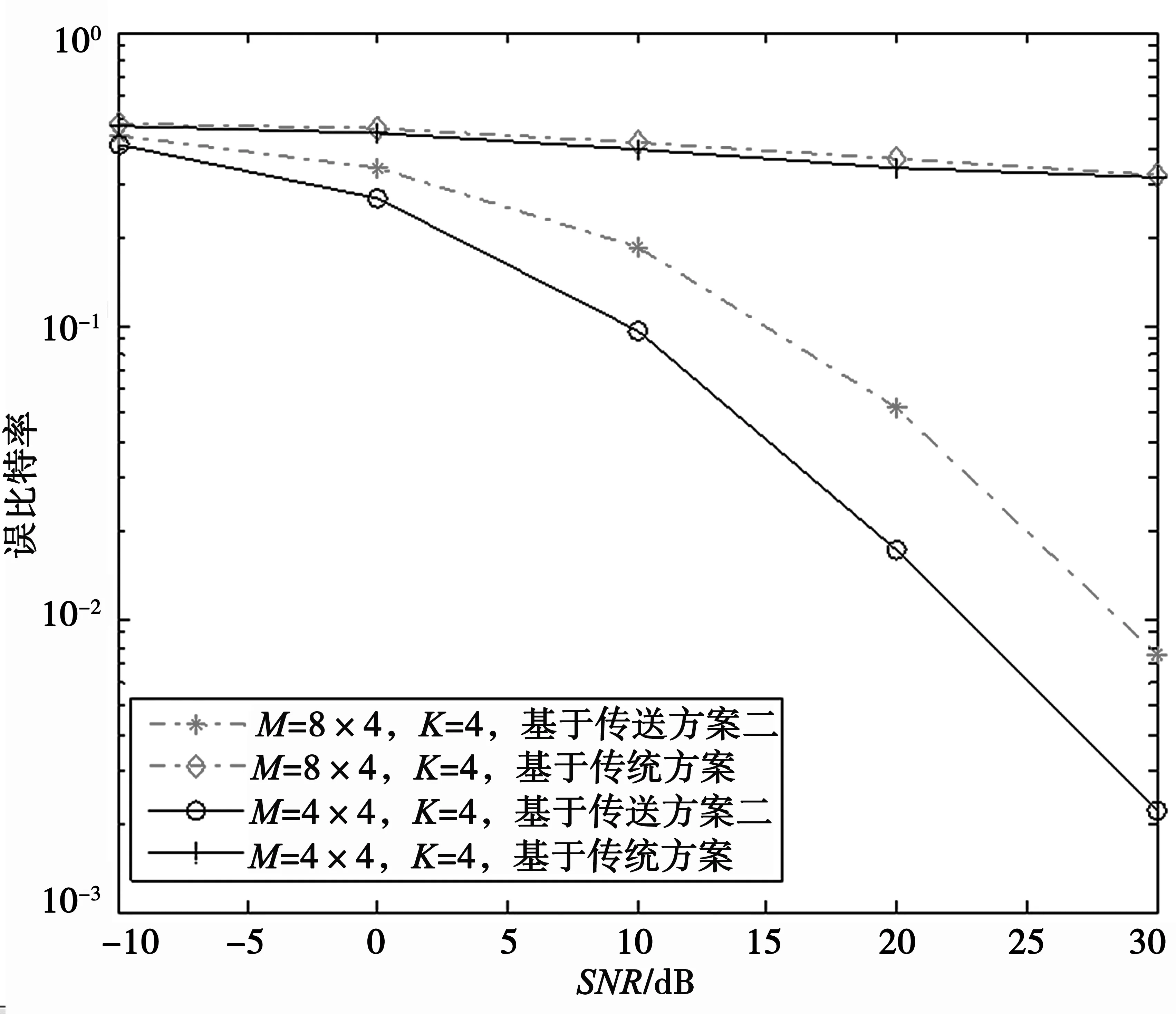
針對基站部署M=Mv×Mh根天線的系統,基于提出的降維矩陣將天線進行合并可得到天線數為N(N 2344 在△ABC中,以BC中點M為圓心,BC為直徑作圓交AB、AC于F、E,連接FC,EB,其交點為D,FE交AD于P,BP、ME交Q,求證:QA∥BC. 仿真環境在前面所述的FD-MIMO 典型場景下,表1 給出了系統仿真時的參數 表1 系統仿真參數設定 圖2 中顯示了在K=2,4,M=24,32 情況下的誤比特率的仿真結果。從圖2 中可以看出,在基站天線數確定的情況下,隨著信噪比的增大,誤比特率在減小;在用戶數確定的情況下,隨著基站天線數的增加,誤比特率也增大。 圖2 單天線下基于仿射投影解碼策略下的仿真結果 圖3 中顯示了在K=2,SNR=10 dB 情況下,可達速率域的仿真結果。從圖3 中可以看出,在用戶數確定的情況下,可達速率域隨著基站天線數的增加而增大,且增加的幅度逐漸變小。 圖3 不同天線配置下的可達速率域 圖4 中顯示了在K=4,M=32,16 情況下,誤比特率的仿真結果。從圖4 中可以看出,在用戶數確定的情況下,隨著基站天線數的增加,誤比特率也增大。在傳統方案中,誤比特率隨著信噪比的增加下降速度非常緩慢;而在所提出的傳送方案二的情況下,誤比特率隨著信噪比的增加,下降速度越來越快。 圖4 單天線下基于循環矩陣策略下的仿真結果 本文研究基于假定發送端對信道狀態信息完全不知道的情況,針對單天線的多用戶大規模MIMO系統,在基站側利用降維矩陣將大規模天線進行有效合并,在用戶端利用仿射投影技術提出了新的解碼策略。該策略充分利用了對角空時碼的特性,可將用戶間的干擾完全消除,進一步解出各個用戶所需要的信息。與此同時,還提出了基于循環矩陣形式的傳送方案和解碼方法,并從理論上分析了所提出解碼策略的性能。最后,對所提出的方案進行了仿真,其結果也與理論分析一致。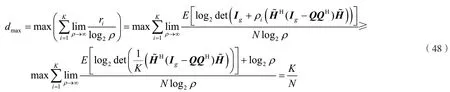
4 仿真結果

4.1 仿真1
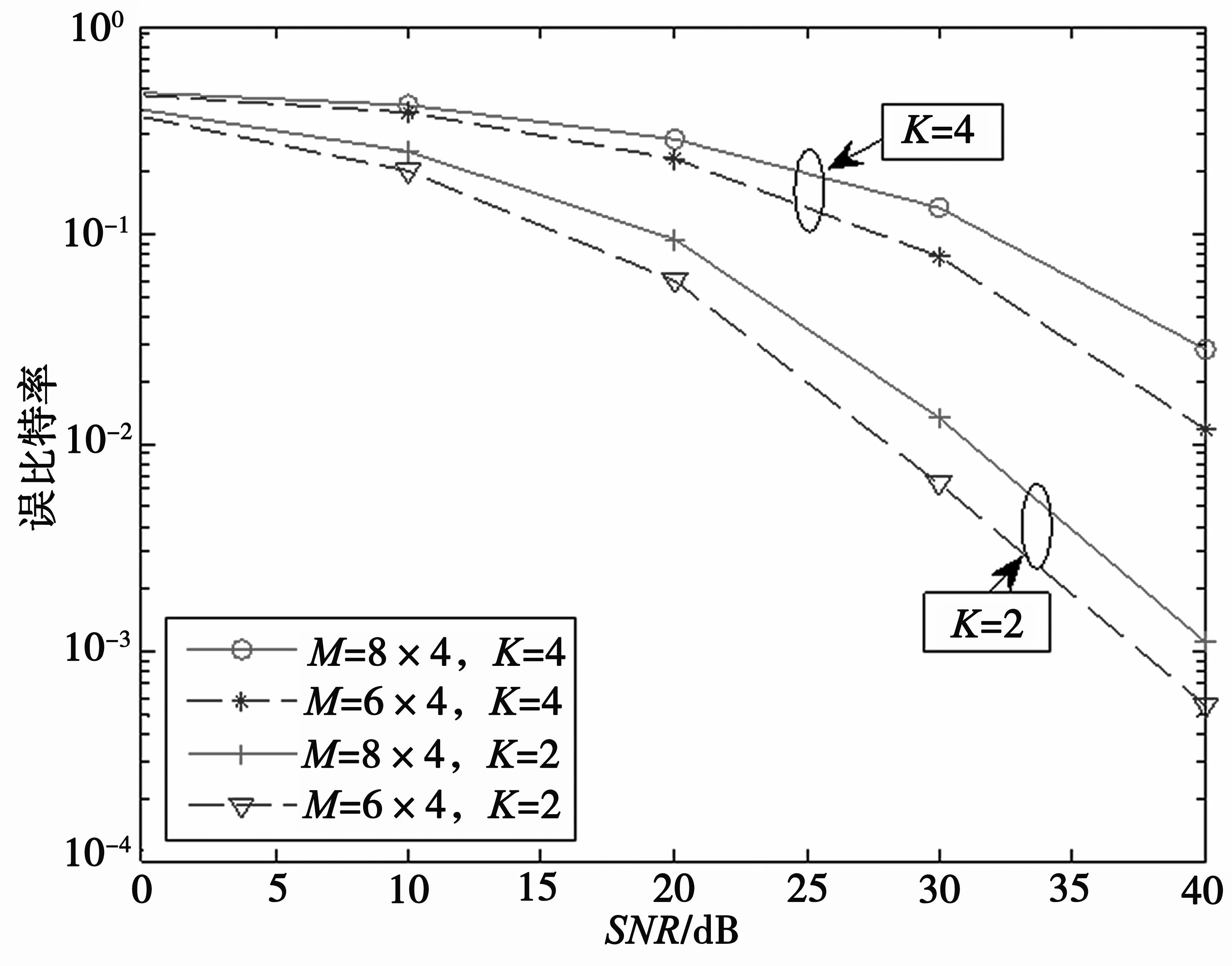
4.2 仿真2

4.3 仿真3
5 結語

