基于矩陣分解的捷聯(lián)慣導多位置系統(tǒng)級標定方法*

趙桂玲，譚茂林，吳 偲

(遼寧工程技術大學測繪與地理科學學院，遼寧 阜新 123000)

捷聯(lián)慣導系統(tǒng)級標定的實質是根據(jù)系統(tǒng)的導航輸出進行慣性測量單元(Inertial Measurement Unit，IMU)誤差參數(shù)的估計[1-3]。IMU誤差參數(shù)標定結果直接影響系統(tǒng)的導航精度，IMU估計精度和標定時間也成為反映系統(tǒng)級標定技術的關鍵指標[4-5]。常用的系統(tǒng)級標定方法分為擬合法和濾波法[6-7]。擬合法的研究集中在標定路徑編排，通過設計合適的標定路徑建立起觀測量與誤差參數(shù)之間的關系，再利用最小二乘估計對誤差參數(shù)進行標定[8]。擬合法路徑編排與待辨識誤差參數(shù)密切相關，計算簡便，但標定模型推導復雜[9]，標定環(huán)境和條件要求嚴格[10]。

濾波法研究集中在設計濾波方案[11-12]，通過建立系統(tǒng)狀態(tài)方程和量測方程，利用Kalman濾波算法對誤差參數(shù)進行估計[13]，鮮有文獻對路徑編排進行深入的理論推導和分析，導致標定位置多、標定時間長。文獻[14]建立了36維Kalman濾波模型，標定路徑為25位置，標定時間約為4 h。文獻[15]設計了一組13位置轉動編排方案，標定21項誤差參數(shù)用時約1 h。文獻[16]以導航速度誤差為觀測量建立了27維Kalman濾波器，設計了一組8位置標定路徑來標定21個誤差參數(shù)，標定時間為40 min。上述文獻未對誤差參數(shù)辨識與路徑設計進行深入的理論分析和探討。文獻[17]對IMU誤差參數(shù)激發(fā)過程進行分析，建立了27維濾波模型，設計了35次序標定路徑，標定時間為2 h，標定路徑過于復雜。上述研究均存在標定時間長，標定路徑復雜等問題。

針對上述問題，本文將安裝誤差角分解為不正交角和正交的失準角，建立非正交和失準的標定模型。將擬合法中路徑編排與誤差參數(shù)辨識緊密聯(lián)系的特點引入濾波法，設計了7位置連續(xù)標定路徑，對誤差參數(shù)的可辨識性、可觀測強度和標定時間進行分析，完成21項誤差參數(shù)的完全標定，標定時間小于30 min。

1 系統(tǒng)模型的建立

1.1 IMU輸出誤差模型

捷聯(lián)慣導系統(tǒng)通常由三個加速度計和三個陀螺組成，加速度計的比力誤差和陀螺的角速率誤差為:

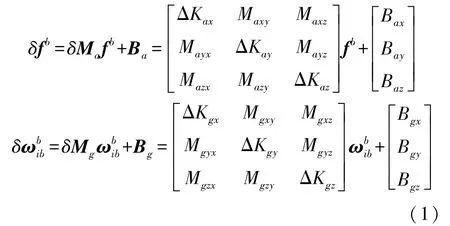
式中:δfb和分別表示加速度計和陀螺的輸出誤差；δMa和δMg是三階方陣，兩個矩陣中主對角線元素分別表示加速度計組件和陀螺組件標度因數(shù)誤差，非主對角線元素表示加速度計組件和陀螺組件安裝誤差；fb和表示IMU理想輸出；Ba和Bg分別表示加速度計和陀螺的零偏誤差。

導航坐標系下觀測量對載體坐標系參數(shù)約束不足，加速度計和陀螺12項安裝誤差系數(shù)存在3組耦合關系[18]。將加速度計或陀螺敏感軸進行重新定義，對載體系參數(shù)形成約束，安裝誤差參數(shù)降為9項。引入矩陣分解原理[19]，將δMa和δMg分解為對稱矩陣(Symmetric matrix)與斜對稱矩陣(Skewsymmetric matrix)之和。和表示對稱矩陣，和表示斜對稱矩陣。

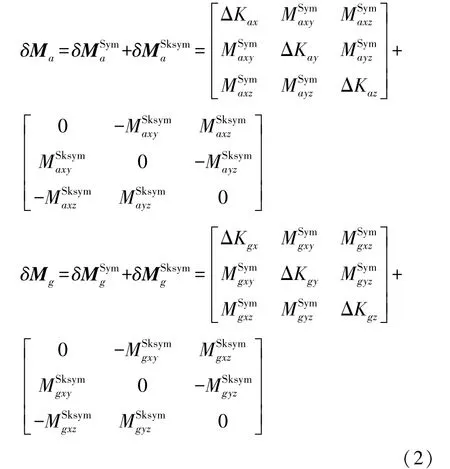
加速度計組件和陀螺組件的安裝誤差特性由非正交特性和正交失準特性構成。非正交特性表現(xiàn)為組件的3個輸入軸不正交，正交失準特性表現(xiàn)為正交組件相對載體系失準。采用最佳約束方式使陀螺斜對稱矩陣為零[19]，對應安裝誤差標定流程如圖1所示。

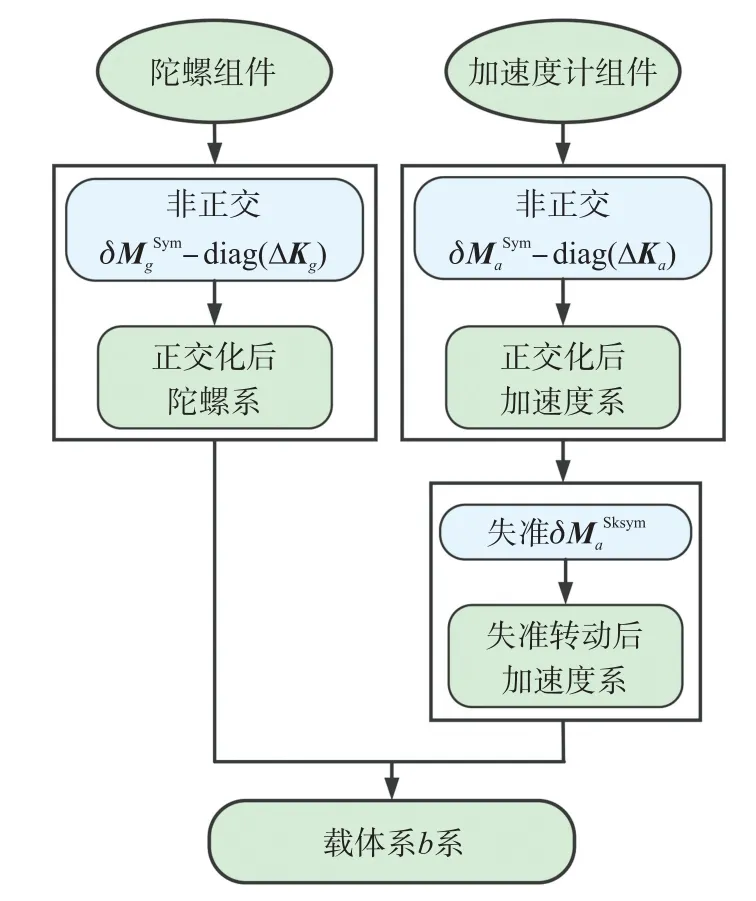
圖1 安裝誤差標定流程

從式(2)和圖1可知，本文對IMU安裝誤差進行分解，安裝誤差角被分解為非正交角和正交的失準角。安裝誤差標定流程為先完成安裝誤差正交化，正交化完成后的組件相對載體系b系失準，需要轉動與b系重合，使IMU完成真正意義上的安裝誤差建模。由于約束關系的存在，本文設計的約束方式是將正交化后的陀螺組件構成的正交坐標系視為與b系重合。由此，系統(tǒng)輸出誤差模型設定為:

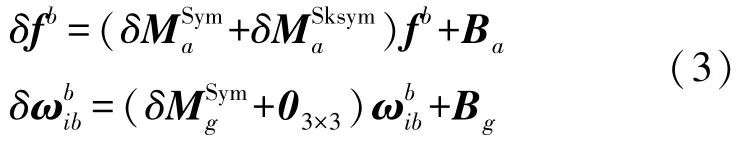
1.2 系統(tǒng)誤差方程

忽略δg影響，略去二階小量，姿態(tài)誤差角φ＝[φxφyφz]T為小角度，靜基座下IMU誤差參數(shù)引起捷聯(lián)慣導系統(tǒng)速度和姿態(tài)誤差方程為:

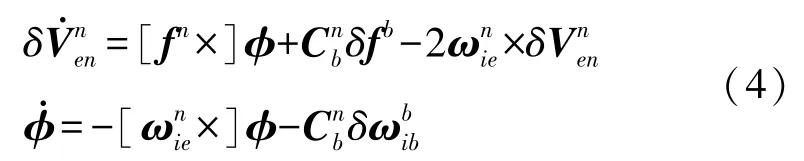
式中:導航坐標系n系選用東-北-天坐標系，載體坐標系b系選用右-前-上坐標系。表示n系下速度誤差，fn表示比力在n系下的投影，表示地球自轉角速度在n系下的投影，δfb和為系統(tǒng)輸出誤差模型中b系下比力誤差和旋轉角速度誤差。表示b系到n系的捷聯(lián)矩陣，靜基座條件下fn＝(說明:ωc、ωs分別為ωiecosL、ωiesinL的簡寫，L為當?shù)氐乩砭暥?。

1.3 Kalman濾波模型

根據(jù)IMU系統(tǒng)輸出誤差模型和系統(tǒng)誤差方程，建立的Kalman濾波狀態(tài)變量為27維:

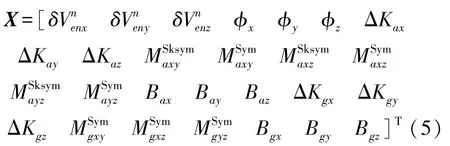
根據(jù)式(4)和式(5)構建濾波器狀態(tài)方程和量測方程:

式中:F為狀態(tài)轉移矩陣，G為系統(tǒng)噪聲分配矩陣，W為IMU輸出中的白噪聲向量，觀測矩陣H＝[I6×606×21]。

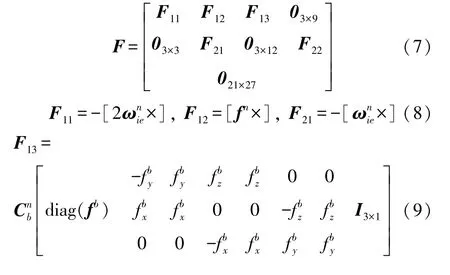
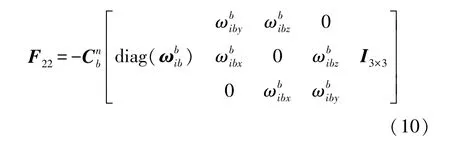
2 標定路徑的設計

2.1 路徑編排

在靜基座條件下，IMU通過敏感重力加速度g和地球自轉角速率ωie完成誤差參數(shù)的標定。由于ωie是一個小量，為更好地激勵陀螺各項誤差參數(shù)，同時保證標定過程的連續(xù)性，通過轉臺施加轉動角速率ωr完成位置變換。

1.2.1 對照組 行單一肛瘺切除術治療:患者手術前進行常規(guī)的灌腸和導瀉,所有患者進行腰-硬聯(lián)合麻醉[3],麻醉后進行常規(guī)消毒,然后鋪巾,等待肛門括約肌松弛舒張后進行肛內消毒。行單一肛瘺切除術治療時首先探針由外口向內口插入,然后將瘺管和內口沿探針切除,沿著切開的瘺管清除所有瘢痕和壞死組織。對患者術后情況觀察并記錄。

設計IMU敏感軸在兩個標定位置分別指向天向和地向快速消除誤差參數(shù)中的部分耦合關系。以“北-東-地”和“北-西-天”兩個位置為例。在“北-東-地”完成靜態(tài)導航后，繞x軸轉動180°到達“北-西-天”。對于IMU靜止在標定位置時，設靜止時間從t0~t1，則在靜止位置下有:

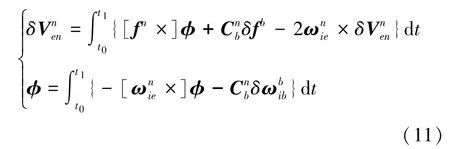
將兩個位置對應的參數(shù)代入式(11)，得兩個位置下的速度誤差和姿態(tài)誤差，如下

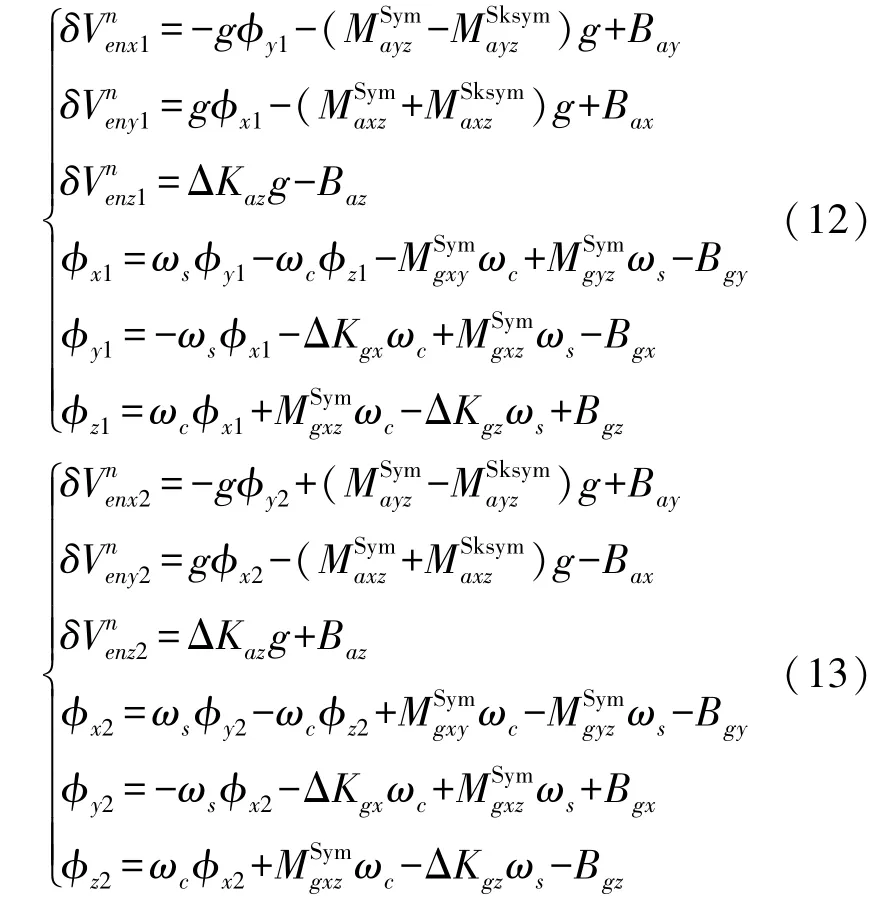
從式(12)和式(13)可看出，兩個位置下速度誤差和姿態(tài)誤差對應被激勵的IMU誤差參數(shù)是相同的，參數(shù)前的正負號不同，聯(lián)立公式即可消除參數(shù)間的耦合關系。通過這種標定位置設計方式可以快速辨識加速度計和陀螺誤差參數(shù)，如下:

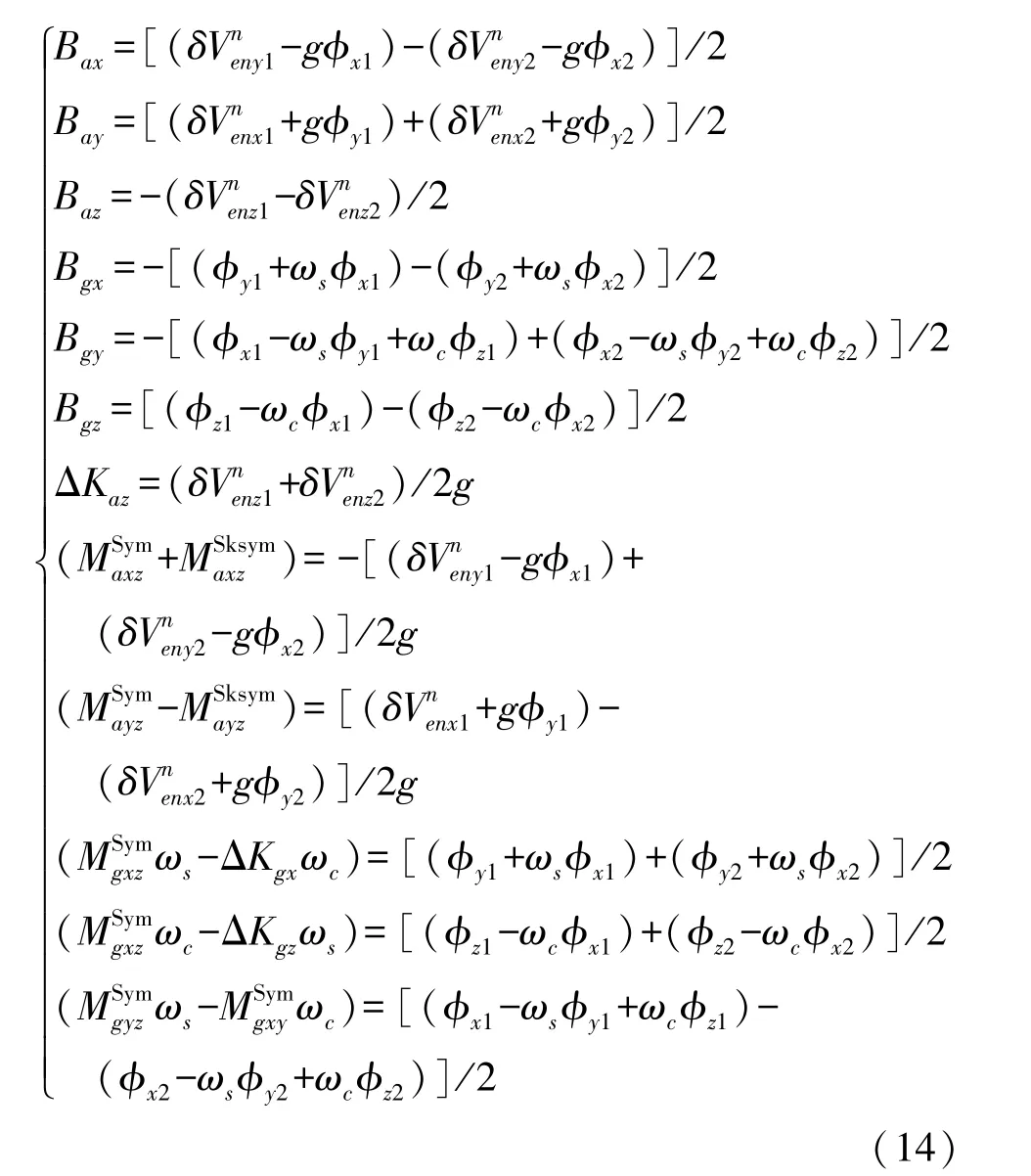
上述兩個標定位置可以直接辨識出7項誤差參數(shù)，另外有9項誤差參數(shù)雖被激勵，但由于存在耦合關系不能被辨識出，剩下的5項參數(shù)則不能被激勵。

IMU從“北-東-地”繞x軸旋轉180°到“北-西-天”，轉臺轉動角速率ωr設計為6°/s，標定中由于ωc?ωr、ωs?ωr，Bgi(i＝x，y，z)?ωr，因此在轉動過程中可忽略地球自轉角速率和陀螺零偏。在t1~t2轉動過程中由陀螺誤差引起的姿態(tài)誤差方程如下:

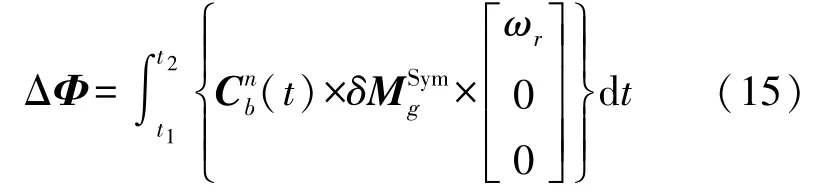
式中:以“北-東-地”為初始位置繞x軸轉動，轉動過程中的捷聯(lián)矩陣為:

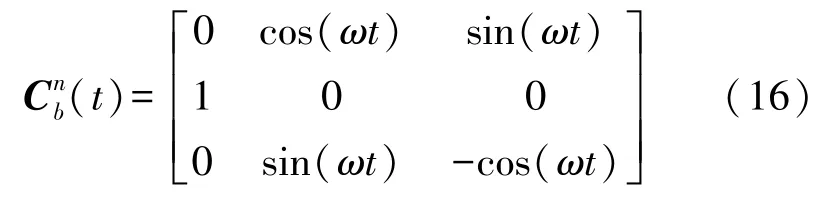
轉動完成后，

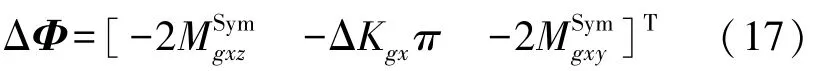
從式(17)可看出，本次轉動可使陀螺3項誤差參數(shù)被辨識出。由于Bgi(i＝x，y，z)?ωr，在轉動過程中難以辨識，在轉臺靜止時進行IMU零偏標定。零偏仿真結果如圖2所示。每個位置靜止600 s，轉動時間為30 s，標定時間共計20.5 min。

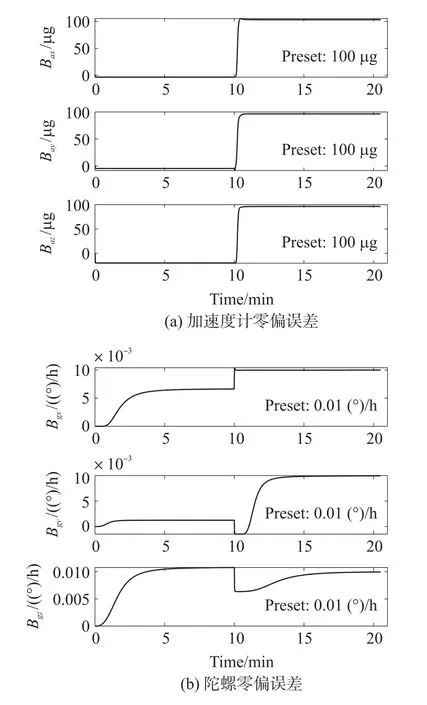
圖2 IMU零偏誤差估計曲線

2.2 標定方案

同一標定路徑下，不同誤差參數(shù)的可觀測度不同。圖2中，加速度計零偏誤差可觀測度高，陀螺可觀測度低。當從“北-東-地”轉換到“北-西-天”時，加速度計3項零偏誤差在很短的時間內達到收斂。陀螺3項零偏誤差的可觀測度差別明顯，Bgx在該路徑下可觀測度強，短時間即達到收斂，Bgy在轉動完成后需要約6min才能收斂，Bgz需要約8 min才能收斂。分析原因，陀螺敏感地球自轉角速率是一個小量，導致陀螺零偏的可觀測度低，需要的標定時間長。綜合考慮加速計和陀螺零偏收斂時間，本文設計標定路徑如圖3所示，前2個位置靜止時間分別為500 s，后5個位置靜止時間分別為120 s。

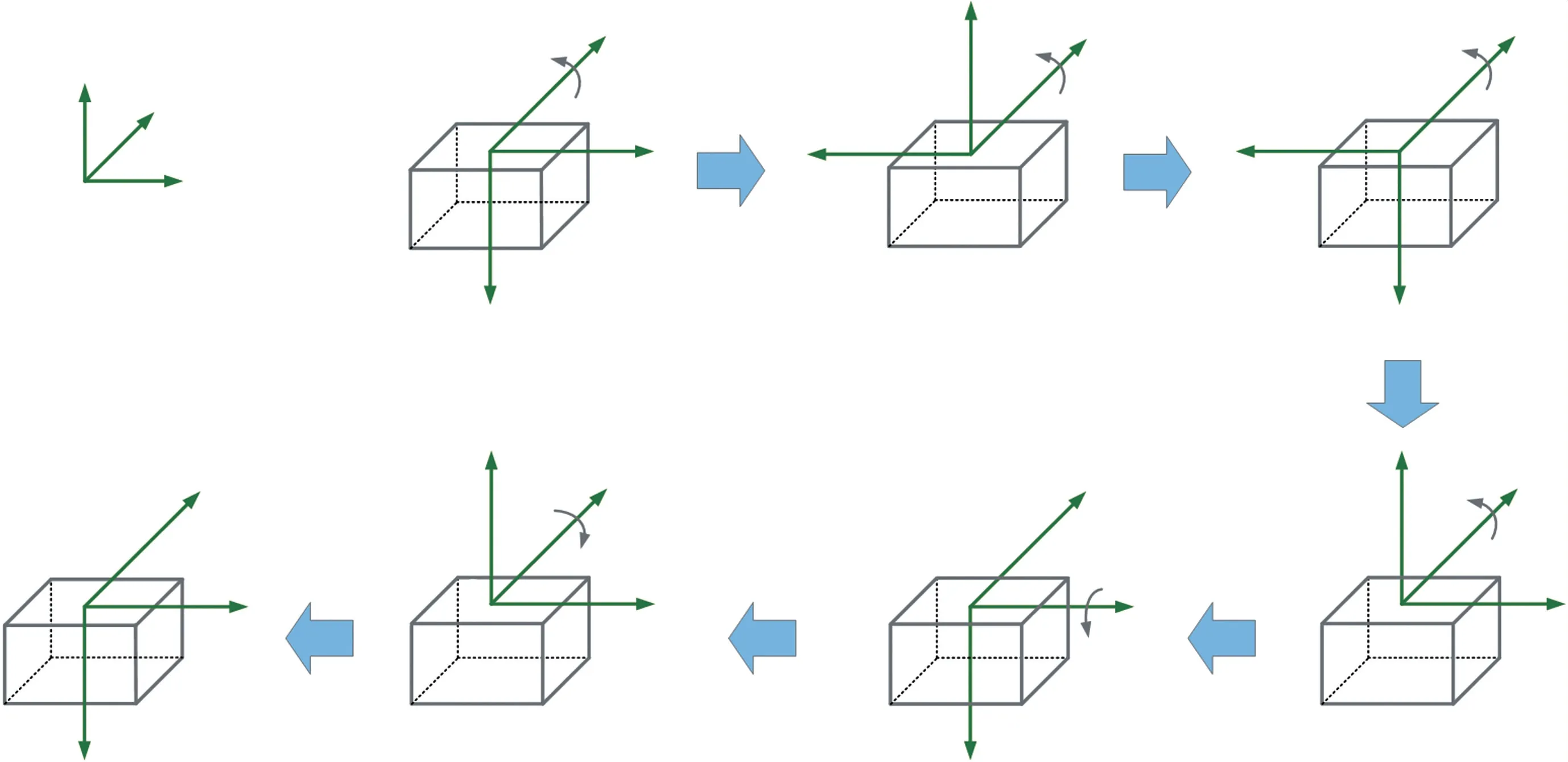
圖3 7位置標定路徑

2.3 可觀測性分析

為驗證標定路徑的有效性，采用分段線性定長系統(tǒng)(Piece-Wise Constant System，PWCS)對路徑進行可觀測性分析。利用提取的可觀測性矩陣(Stripped Observability Matrix，SOM)代替總的可觀測性矩陣，使得模型的可觀測分析變得更簡單[20]。

根據(jù)Kalman濾波器的狀態(tài)方程和量測方程，可觀測性矩陣SOM為:

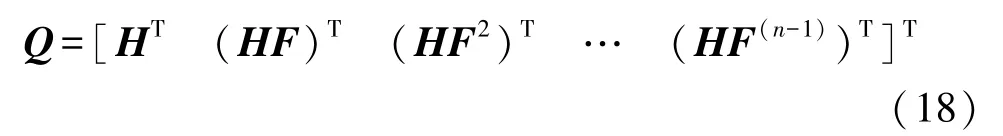
式中:Q代表矩陣SOM，n為Kalman濾波器狀態(tài)維數(shù)，為27維。計算SOM在各位置下的秩，結果如圖4。

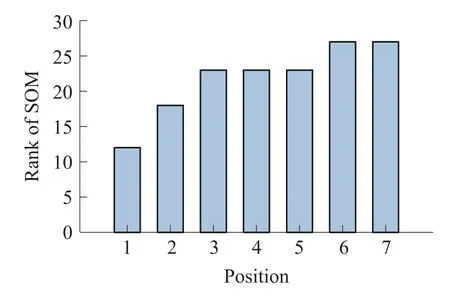
圖4 各位置下可觀測矩陣的秩

從圖4可以看出，系統(tǒng)在第六個位置時，SOM的秩達到27，等于濾波器狀態(tài)維數(shù)。可以判定系統(tǒng)狀態(tài)在該路徑下完全可觀測[21]，驗證了論文設計路徑的可行性。

3 實驗結果與分析

對7位置系統(tǒng)級標定算法進行仿真實驗。初始速度設置為V0＝03×1，3個初始姿態(tài)角分別設置為:航向角270°，俯仰角0°，橫滾角180°，采樣頻率設置為100 Hz。各誤差參數(shù)的預設值見表2。濾波估計曲線如圖5~圖10所示。

從圖5~圖10中可以看出，各誤差參數(shù)都能完全收斂，估計結果見表1。

圖5 加速度計零偏誤差估計曲線

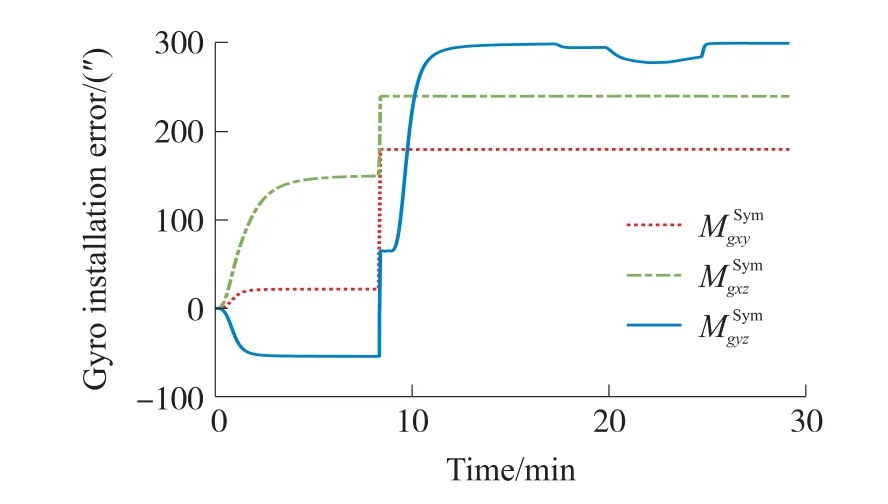
圖10 陀螺安裝誤差估計曲線

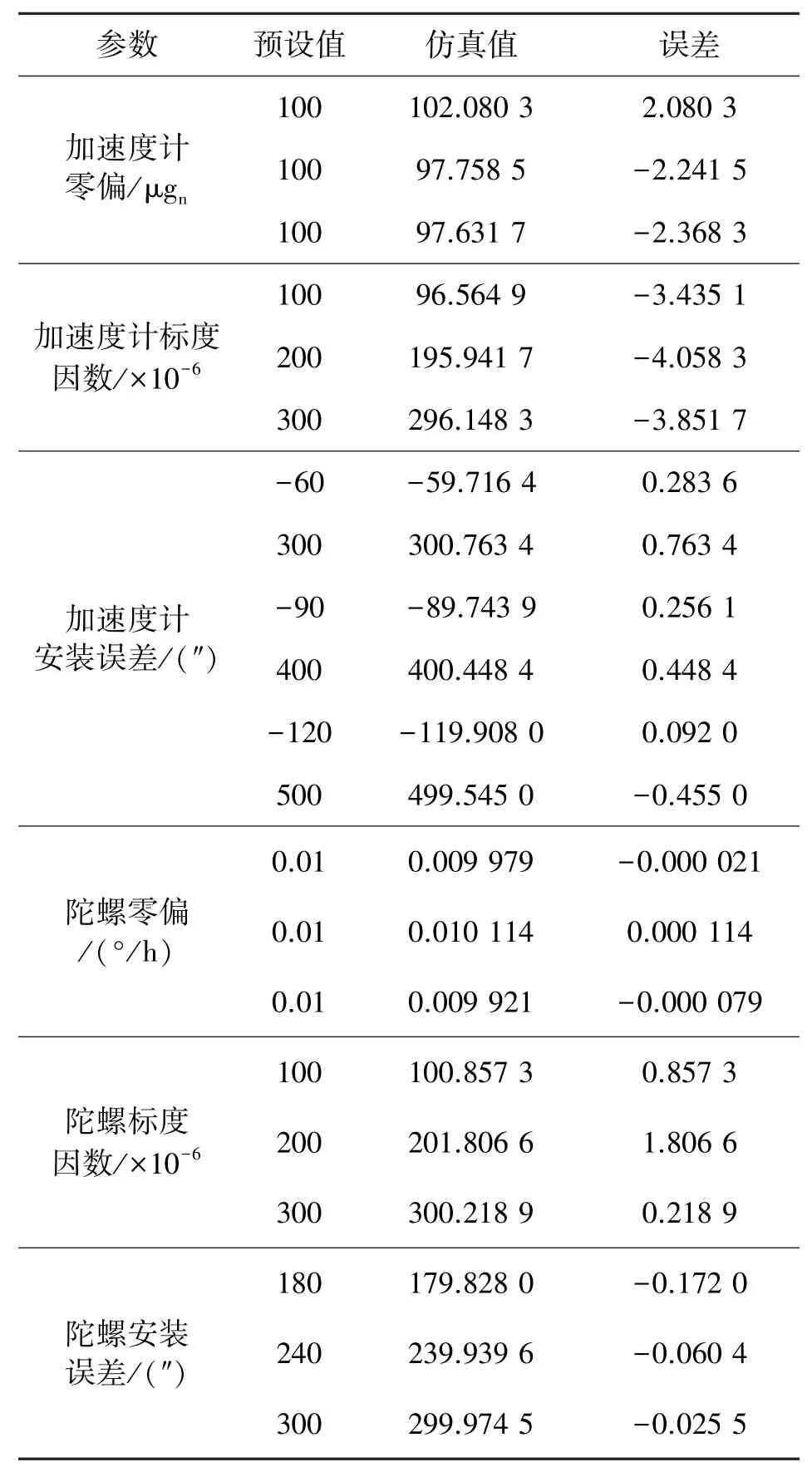
表1 標定誤差估計結果

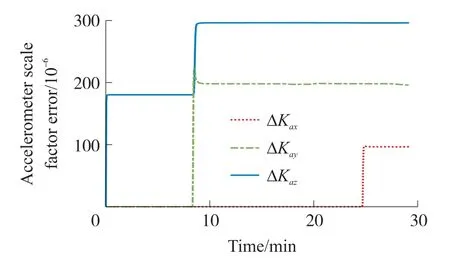
圖6 加速度計標度因數(shù)誤差濾波估計曲線

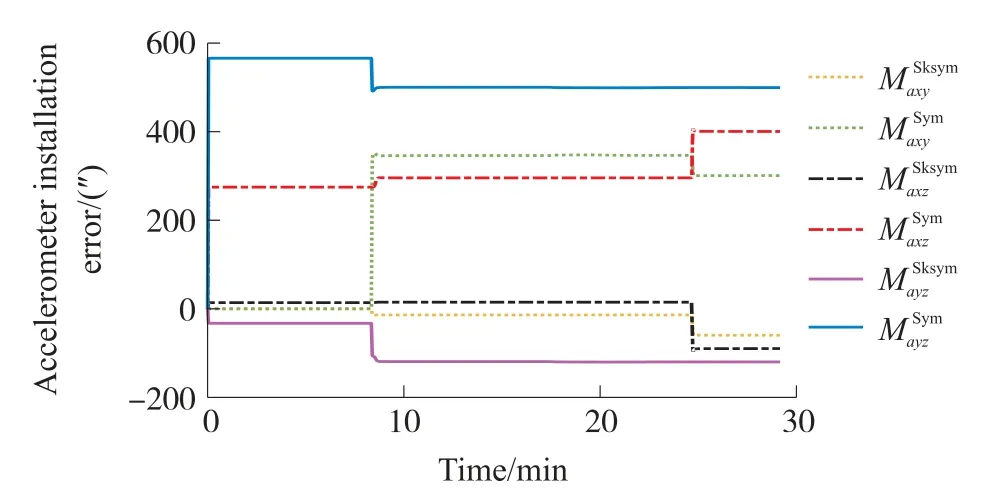
圖7 加速度計安裝誤差估計曲線

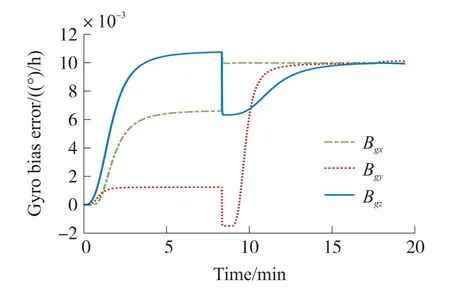
圖8 陀螺零偏誤差估計曲線

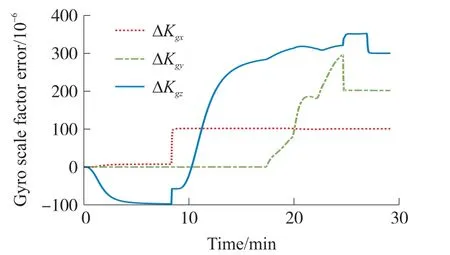
圖9 陀螺標度因數(shù)誤差估計曲線

計算IMU待標定參數(shù)估計結果，陀螺零偏誤差優(yōu)于0.000 15°/h，加速度計的零偏誤差優(yōu)于3μgn，陀螺標度因數(shù)誤差優(yōu)于2×10-6，加速度計的標度因數(shù)誤差優(yōu)于4.5×10-6，安裝誤差角優(yōu)于1″。

為驗證基于矩陣分解的捷聯(lián)慣導多位置系統(tǒng)級標定方法的可靠性，另設置3組不同的安裝誤差參數(shù)，分別為表1中安裝誤差參數(shù)預設值的40%、60%、80%(組1~組3)，進行仿真對比實驗。

表2以各組中加速度計和陀螺安裝誤差參數(shù)估計精度最低的誤差項作為安裝誤差的估計誤差，IMU各項安裝誤差標定精度均優(yōu)于1″。

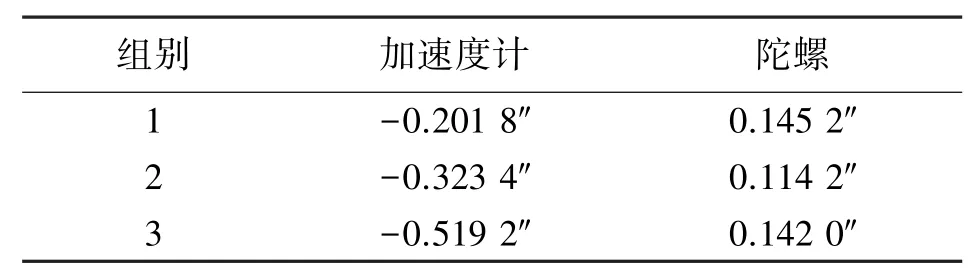
表2 對比實驗安裝誤差估計誤差

4 結論

本文基于矩陣分解原理對安裝誤差矩陣進行分解，將安裝誤差矩陣分解為對稱矩陣和斜對稱矩陣之和，對應地將安裝誤差角分解為不正交角和正交的失準角，建立了包含21項誤差參數(shù)的標定誤差模型。以導航速度誤差和姿態(tài)誤差為觀測量，建立27維Kalman濾波模型。深入分析標定路徑與誤差參數(shù)辨識間的關系，根據(jù)陀螺和加速度計零偏可觀測度的不同設置標定時間，設計了一種7位置標定編排方案，誤差參數(shù)在標定結束后全部收斂，標定時間小于30 min。仿真實驗驗證了所提方法和標定路徑的可行性。本文為系統(tǒng)級標定濾波法的路徑編排提供了一些新思路，具有良好的工程參考價值。