多跨曲線連續梁橋結構受力及穩定性分析

蘇越

（華杰工程咨詢有限公司，北京 100020）

0 引言

在現代公路交通工程中，多跨曲線連續梁橋是一種常見橋型。在公路橋梁工程中，一般應做到橋梁平面與公路路線二者相契合，因此要求在設計階段應確保橋梁線形平順明快，橫縱斷面布置合理。在這樣的情況下，多跨曲線梁橋是設計人員的首選橋型。與一般梁橋不同，多跨曲線梁橋適應性強，不受地形限制，且梁橋整體線性流暢，工程美感好。若將曲線梁橋應用于分布廣泛的山區公路，一方面可以較好地利用現有的地形條件，另一方面能夠使道路避免不良地質條件，降低工程整體造價。若將曲線梁橋應用于城市立交橋及高架橋工程建設中，不但可以實現交通轉向功能，而且不受地下管道、線路及沿街建筑的影響，可以減少建設用地面積，提高工程經濟合理性。

多跨曲線連續梁橋這一橋型在高速公路、城市立交橋及高架橋工程建設中應用廣泛，然而多跨曲線連續梁橋在應用過程中也存在一些工程病害，因此，針對多跨曲線連續梁橋結構開展結構受力和穩定性變得勢在必行。如圖1 所示的北京市東城區的互通式立交橋，該橋為多跨預應力混凝土曲線梁橋。

圖1 北京市東城區的互通式立交橋

1 工程概況

某項目互通匝道橋選型為多跨曲線連續梁橋，表1 是橋梁基本參數，表2 為橋梁主要技術指標。

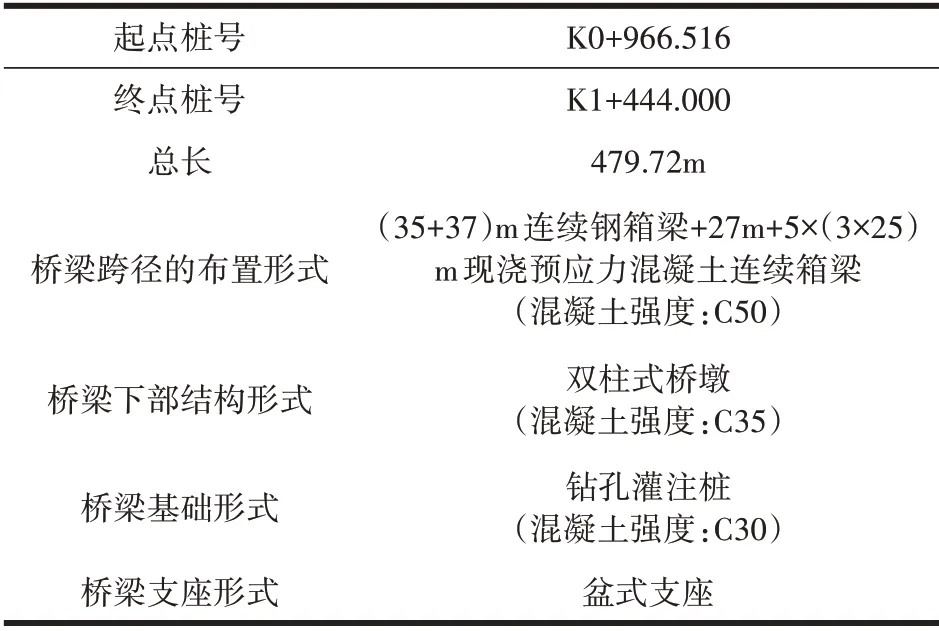
表1 橋梁基本參數

表2 多跨連續梁橋主要技術指標

2 多跨曲線連續梁橋力學特征及結構受力分析

2.1 多跨曲線連續梁橋結構力學特性

按橋梁線形分類，橋梁可以分為曲線梁橋、直線梁橋和斜梁橋。與直線梁橋和斜梁橋不同的是，在上部荷載作用下多跨曲線梁橋會產生豎向變形，在豎向變形的同時，由于受到橋梁曲線率半徑的影響，曲線梁橋梁體會出現扭轉，從而進一步促進曲線梁橋豎向變形的發展。這種彎曲變形和扭轉變形耦合交互作用的現象，被簡稱為“彎扭耦合”效應。在這種效應的持續作用下，多跨曲線連續梁橋的受力變形有以下特征：

2.1.1 豎向荷載值相同時，由于“彎扭效應”的存在，多跨曲線梁橋發生的變形值大于直線梁橋。并且，曲線梁橋外側的變形值大于內側。且有如下規律：橋梁跨度相同時，曲率半徑值越小，橋面寬度越大，曲線梁橋的上述特征愈顯著。

2.1.2 對于多跨曲線連續梁橋，若在橋梁上側作用有對稱分布的豎向荷載，曲線梁橋仍會發生扭轉現象。同時，橋梁內外截面處的應力分布規律也明顯不一致，橋梁外側截面應力數值較大且分布集中，橋梁內側截面應力數值較小且分散。

2.1.3 通過對曲線橋梁支座受力分析可知，橋梁上部的豎向荷載值相同時，直線梁橋支座內外相差不大，而曲線梁橋的支座受力，外側大于內側，并且越往支座的外側偏移，支座的受力越大，呈遞增的現象。影響支座受力的主要因素是曲率半徑，曲率半徑越小，支座受力越不均，相反，曲率半徑越小，支座內外側受力越均勻。

2.1.4 多跨曲線梁橋的支座受力值與多種因素密切聯系。對于該工程中5×（3×25）m 現澆預應力混凝土連續箱梁梁體而言，采用的預應力鋼束裝置對支座受力有著顯著影響。

2.2 多跨曲線連續梁橋結構受力影響因素

根據多跨曲線連續梁橋受力分析可知，梁橋的受力特征不僅受到豎向荷載作用點、梁體跨度值L、曲率半徑值及橋面寬度B 等因素的影響，還與下列因素有關：

2.2.1 多跨曲線梁橋曲率半徑對應的圓心角φ。一般而言，曲率半徑值越大，對應的圓心角也越大，曲線梁橋彎曲程度也越大。在這種情形下，梁橋整體的受到的彎扭耦合作用也越嚴重，對梁橋受及變形處于不利情形。當圓心角不超過30 度時，不需考慮考慮扭轉作用對梁橋變形的影響。根據研究表明，曲線梁橋圓心角不超過50 度時，曲線梁橋的縱向彎矩可按照直線梁橋考慮，計算結果符合要求。

2.2.2 多跨曲線連續梁橋橋面寬度B 與曲率半徑的比值。在車輛產生的偏心荷載的作用下，由于彎扭耦合作用的存在，梁體內部會產生彎矩與扭矩。若曲率半徑維持不變，橋面寬度B 越大，彎扭耦合作用則越顯著，這樣梁體受力及變形均處于不利情形。當橋面寬度B 過大，而曲率半徑又較小時，梁橋內側的弧長遠遠小于外側弧長。在荷載計算時，內側的荷載要小于外側荷載。曲線梁橋的受力分析沒有完整的體系，因此將曲線梁橋看作是直線梁橋進行受力分析。若曲線梁橋不滿足以下公式，便不能簡化為直線梁橋進行受力分析：

式（1）中：L——梁體跨度值；R——橋梁中線半徑；b——橋梁寬度值的一半。

2.2.3 彎扭剛度比值k=EI/GI。彎扭剛度比k對多跨曲線梁橋的受力與變形起到決定性作用。在單位集中荷載作用下，隨著k 值的逐漸增大，曲線梁橋發生的扭轉變形值越來越大。因此，在多跨曲線連續梁橋設計中，當梁體的抗彎剛度EI 符合規范要求時，應采取措施來提高梁體的抗扭剛度GI，從而減小曲線梁橋因扭矩產生的變形。

2.2.4 在開展結構中，需慮薄壁效應的影響。與直線梁橋不同，曲線梁橋截面在受力變形后無法維持在原有平面內。對于混凝土結構而言，薄壁效應并不顯著，且該工程中采用的連續箱梁形狀接近正方形當橫截面產生的翹曲變形低于某一限值時，可忽略薄壁效應的影響。圖2 為箱梁的薄壁效應。

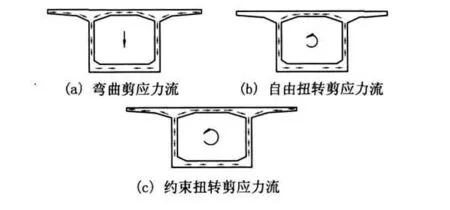
圖2 箱梁的薄壁效應

2.3 多跨曲線連續梁橋結構受力分析理論

目前，針對多跨曲線連續梁橋受力分析有著多種類型的計算方法，主要采用以下兩類計算方法：

第一類是將彎曲梁橋簡化為單曲梁，根據純扭轉力學理論對單曲梁截面進行力學分析，從而得到橫向應力分布情況。這種方法理論成熟，計算簡便，與直線梁橋的計算方法類似，但對于變截面曲線梁橋及變半徑曲線梁橋這一方法存在局限性，并且完橋的橫向應力計算理論發展不夠成熟，影響計算結果的精度。

第二類是數值模擬計算方法，比如有限元有限條法。在這一計算方法中，會根據曲線梁橋實際工況建立梁板單元，梁板有若干個一定尺寸的小方塊組成，從而可以較好地模擬曲線梁橋。根據梁橋的受力情況給模型施加荷載，輸入程序語言對模型開展受力及變形分析，然而這一方法受到單元格劃分等因素的影響，且計算量大，一般通過大型計算機解決。

3 多跨曲線連續梁橋穩定性分析與抗傾覆驗算

3.1 多跨曲線連續梁橋穩定性分析

曲線梁橋多存在于高速公路匝道或者地理位置特殊的地段，為了使橋梁的等級達到相應的等級，曲線連續梁橋的設計也存在很多難題，比如：

3.1.1 城市內的多跨連續橋梁，某些為了滿足整體城市道路的需要，橋墩必須設計成獨立墩，獨立墩柱占地面積小，對城市的整體布局影響不大。圖3 為城市常見的橋梁獨立墩柱。

圖3 城市橋梁獨立墩柱。

3.1.2 或者對橋梁下部凈高有所規定，曲線梁橋的高度就必須規定要求；曲線梁橋的主梁高度必須適應城市的整體規劃，從而限制了梁截面的選擇。

路面行駛的車輛在曲線梁橋的外側行駛，會導致支座外力加大，加大了傾覆的危險。并且，城市內大多數為獨立墩柱，再次加劇了傾覆的危險。國內已有多起關于獨立墩柱傾覆的新聞。2021年，湖北高速大橋發生了橋面傾覆事故，如圖4 所示，橋面整體傾覆，損傷慘重。經研究發現，改載貨車承載貨物高達198噸，超出了橋梁最大承受荷載，除此之外，橋梁的墩柱形式為獨立墩，在出現偏載時，橋面更容易發生傾覆。度墩柱優勢眾多，比如占地面積小，不影響城市的整體規劃。但獨柱墩的安全問題也備受關注，度墩柱在偏載時易出現傾覆。因此，在以后的設計和研究中，應更加注重度墩柱的穩定性問題，提高度墩柱的安全性。

圖4 多跨曲線梁橋傾覆

3.2 多跨曲線連續梁橋的橫向抗傾覆驗算

曲線箱梁橋由于存在“彎扭耦合”作用，為了避免此現象，可選用抗扭效果好的箱型截面。箱型截面抗扭效果好，且主梁高度較小，符合城市規劃。箱梁的結構特點是：寬度大、懸臂多。正因為此特點，行駛的車輛更容易在墩柱外側出現偏載，使橋梁傾覆。曲線梁橋傾覆的主要原因可以總結如下：因為箱型梁橋的結構特點，車輛在梁橋平曲線外側超載，導致抗傾覆力矩小于傾覆力矩，橋梁結構破壞，圖5 為直線和曲線梁橋傾覆軸線。

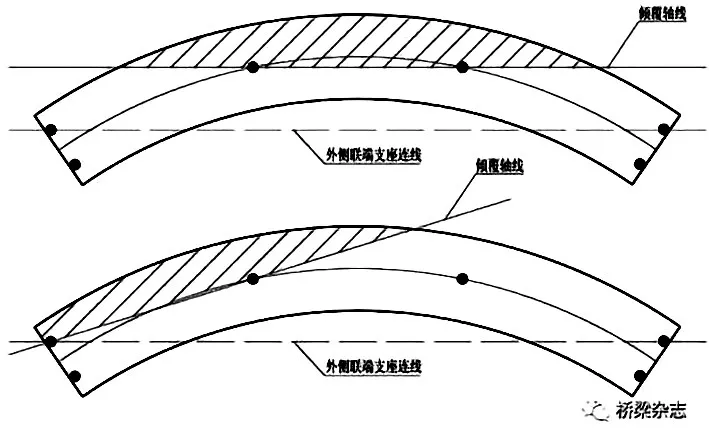
圖5 梁橋傾覆軸線

目前，橋梁抗傾覆的設計標準是：抗傾覆力矩/傾覆力矩＞2.5。采用此原則進行橋梁設計。為了降低橋梁傾覆事故，本文搜集了相關的計算方法，現列舉如下：

3.2.1 《公路橋涵設計通用規范》（JTG D60—2015）中規定的荷載組合計算結果，能夠保證支座不出現反力，始終受壓；

3.2.2 調整汽車荷載的分項系數。同濟大學調查上海市超載情況，將汽車荷載的分項系數提高至3.4，既能保證橋梁抗傾覆性能，也不會存在設計過剩的問題；

3.2.3 對于縱橫坡較大的橋梁多采用墩梁固結的形式，抗傾覆驗算的同時需要對墩柱抗拔能力進行驗算。

4 結論

其一，本文以多跨曲線連續梁橋為研究對象，分析曲梁與直梁的受力特點，研究多跨曲線梁橋的結構優勢和特點；其二，以實際工程為研究基礎，分別從多跨曲線梁橋曲率半徑對應的圓心角φ、多跨曲線連續梁橋橋面寬度B 與曲率半徑的比值、彎扭剛度比值k以及薄壁效應四個方面，探討多跨曲線連續梁橋結構受力影響因素；其三，從城市發展規劃角度，分析曲線梁橋傾覆的原因，并提出避免梁橋傾覆的具體設計方法。