層理灰?guī)r抗拉力學(xué)參數(shù)各向異性及破裂特征分析
黃 殷 婷,左 雙 英,鐘 帥,劉 博
(1.貴州大學(xué) 資源與環(huán)境工程學(xué)院,貴州 貴陽 550025; 2.貴州大學(xué) 喀斯特地質(zhì)資源與環(huán)境教育部重點(diǎn)實(shí)驗(yàn)室,貴州 貴陽 550025)
0 引 言
巖體內(nèi)部存在的層理、節(jié)理、裂隙等結(jié)構(gòu)面導(dǎo)致了其具有明顯的各向異性[1]。同時(shí)試驗(yàn)研究和工程實(shí)踐表明層狀巖體在荷載作用下的側(cè)向變形及破裂與張拉裂紋的累積和擴(kuò)展密切相關(guān),常常表現(xiàn)為拉破壞,嚴(yán)重危及到邊坡、基坑、洞室頂板、高位危巖體處置等工程的安全[2-4],因此,開展巖體在受拉狀態(tài)下各向異性力學(xué)特性及破裂特征研究具有重要意義。
巴西劈裂試驗(yàn)是測試巖石抗拉強(qiáng)度的間接拉伸方法之一,國內(nèi)外學(xué)者利用巴西劈裂試驗(yàn)開展了一系列巖體抗拉各向異性的研究。劉運(yùn)思等[5]結(jié)合單弱面理論,對(duì)板巖進(jìn)行巴西劈裂試驗(yàn),建立了抗拉強(qiáng)度與層理傾角之間的關(guān)系式,發(fā)現(xiàn)板巖抗拉強(qiáng)度隨層理傾角增大而減小。Dan等[6]對(duì)砂巖、片麻巖、板巖進(jìn)行巴西劈裂試驗(yàn),研究層理傾角、加載方向角對(duì)抗拉強(qiáng)度和破壞模式的影響。Abbass等[7]研究發(fā)現(xiàn),隨著層理傾角的增大,板巖抗拉強(qiáng)度、裂縫長度和圓盤試樣破壞所需的能耗逐漸降低。武鵬飛[8]、許多等[9]對(duì)煤巖進(jìn)行了劈裂試驗(yàn),發(fā)現(xiàn)沿垂直層理方向進(jìn)行加載裂紋更易傳播與擴(kuò)展。楊志鵬等[10]針對(duì)頁巖做了劈裂試驗(yàn),發(fā)現(xiàn)隨層理傾角增加,頁巖試件破裂產(chǎn)狀由直線型向曲弧形過渡。鐘帥等[11-12]對(duì)7組不同角度層理灰?guī)r進(jìn)行巴西劈裂試驗(yàn),根據(jù)巖石聲發(fā)射累計(jì)振鈴次數(shù)定義拉裂損傷變量,推導(dǎo)了抗拉強(qiáng)度、劈裂模量及損傷變量隨層理傾角的變化規(guī)律,并建立了橫觀各向同性本構(gòu)關(guān)系。
三維激光掃描技術(shù)能精確提取掃描對(duì)象三維空間坐標(biāo)數(shù)據(jù),部分學(xué)者通過掃描巖體破裂面,對(duì)細(xì)觀破裂面形態(tài)及結(jié)構(gòu)面統(tǒng)計(jì)參數(shù)進(jìn)行了研究。黃達(dá)等[13]結(jié)合三維激光掃描與掃描電鏡技術(shù),發(fā)現(xiàn)三軸高應(yīng)力條件下卸荷破裂的大理巖破裂面細(xì)微觀斷裂性質(zhì)與圍壓的卸荷速率和初始應(yīng)力狀態(tài)密切相關(guān)。陳珺等[14]對(duì)黑砂巖進(jìn)行直接拉伸與拉伸剪切試驗(yàn),通三維掃描技術(shù),總結(jié)了拉應(yīng)力下巖石破裂面粗糙度隨應(yīng)力狀態(tài)的變化規(guī)律,探討了不同破裂機(jī)制對(duì)破裂面形貌的影響。而粗糙度作為評(píng)估結(jié)構(gòu)面起伏程度的參數(shù)之一,常用來定量評(píng)價(jià)拉裂與剪切破壞狀態(tài)。彭守建等[15]發(fā)現(xiàn)采用粗糙度JRC評(píng)價(jià)結(jié)構(gòu)面各向異性時(shí),劈裂斷裂結(jié)構(gòu)面與剪切斷裂結(jié)構(gòu)面各向異性差異較大。陳世江等[16]則通過比較已有結(jié)構(gòu)面粗糙度的定量表征方法,發(fā)現(xiàn)分形維數(shù)是結(jié)構(gòu)面粗糙度定量描述的有效方法。
以上研究成果主要展現(xiàn)了層狀巖體抗拉力學(xué)特性及破壞裂縫走向與層理傾角有強(qiáng)烈相關(guān)性,也針對(duì)單一結(jié)構(gòu)面不同區(qū)域粗糙度量化參數(shù)進(jìn)行了評(píng)價(jià)與比較,但對(duì)于在巴西劈裂試驗(yàn)條件下受層理結(jié)構(gòu)影響的破裂面各向異性特征及定量化研究較少涉及。因此,本文基于不同層理傾角灰?guī)r的巴西劈裂試驗(yàn),研究層理傾角對(duì)應(yīng)力-應(yīng)變曲線的影響以及灰?guī)r力學(xué)參數(shù)的各向異性特征,觀測灰?guī)r宏-細(xì)觀破壞形態(tài)與裂縫擴(kuò)展過程,利用三維激光掃描技術(shù)與結(jié)構(gòu)面粗糙度量化參數(shù),對(duì)不同層理傾角灰?guī)r破裂面內(nèi)部發(fā)展過程與力學(xué)演化機(jī)制進(jìn)行綜合探討,為進(jìn)一步完善層狀巖體張拉破壞內(nèi)部演化機(jī)制研究提供參考。
1 試驗(yàn)方案
1.1 試樣材料
試驗(yàn)巖樣為三疊系大冶組中風(fēng)化中厚層狀灰?guī)r。將層理面與水平面夾角θ定義為層理角傾角,鉆取直徑50 mm、厚度25 mm的試樣塊并進(jìn)行端面研磨,保證上下兩端平行度在±0.05 mm以內(nèi),表面平整度控制在±0.03 mm以內(nèi),所有試樣均在室溫干燥環(huán)境中保存。每個(gè)角度3個(gè)試樣,共21個(gè)試樣,部分樣品如圖1所示。
1.2 試驗(yàn)設(shè)備及方法
本次試驗(yàn)采用WAW-1000kN型微機(jī)控制電液伺服萬能試驗(yàn)機(jī)對(duì)試樣進(jìn)行加載。DH3818靜態(tài)應(yīng)變數(shù)據(jù)采集儀記錄加載過程中巖體的累積應(yīng)變值。試樣表面前后對(duì)稱,布置兩條長20 mm、寬3 mm的應(yīng)變片(見圖2),設(shè)定壓力機(jī)加載速率為0.05 kN/s。
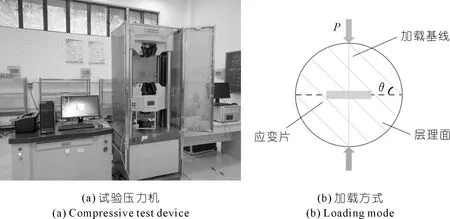
圖2 試驗(yàn)儀器及加載方式示意Fig.2 Schematic diagram of test instrument and loading mode
為了定量分析不同層理傾角巴西劈裂試驗(yàn)過程中破裂面的細(xì)觀結(jié)構(gòu)特征變化規(guī)律,本文采用福建銳品科技有限公司出品的高精度三維激光掃描儀對(duì)巖樣的主破裂面進(jìn)行掃描測試。掃描儀由兩個(gè)ONSEMI工業(yè)測量傳感器(363萬像素,1280×800)、結(jié)構(gòu)光柵發(fā)生器以及支架組成,如圖3所示。掃描儀單幀精度可達(dá)±0.04 mm,掃描速度≤0.3 s,利用該掃描儀可對(duì)巖樣破裂面進(jìn)行多視角測量并進(jìn)行全自動(dòng)拼接,可輕松獲取高精度表面三維數(shù)據(jù)與紋理信息,真實(shí)展示破裂面形貌特征,為進(jìn)一步參數(shù)計(jì)算提供數(shù)據(jù)支持。

圖3 三維掃描儀器設(shè)備Fig.3 3D laser scanner
2 不同傾角層理灰?guī)r抗拉力學(xué)參數(shù)各向異性分析
2.1 拉應(yīng)力-應(yīng)變曲線
試驗(yàn)過程中,可以采集到圓盤試件的豎向荷載,計(jì)算出巖石的水平拉應(yīng)力[17]:
(1)
式中:P為任意時(shí)刻的豎向荷載,kN;D為圓盤直徑,mm;t為圓盤厚度,mm。當(dāng)P達(dá)到最大值時(shí),σmax即為抗拉強(qiáng)度。
繪制水平拉應(yīng)力-應(yīng)變曲線如圖4所示。可以觀察到各個(gè)層理傾角巖樣對(duì)應(yīng)的應(yīng)力-應(yīng)變曲線差異較大,但總體仍表現(xiàn)出孔隙壓密、彈性變形和破壞3個(gè)階段。加載初期,由于灰?guī)r內(nèi)部存在孔隙或微裂縫,試樣表面與加載板接觸后先產(chǎn)生了局部壓密變形,隨后很快進(jìn)入彈性變形階段,隨著荷載增大,變形曲線近似呈直線上升趨勢。應(yīng)力隨著應(yīng)變的增加到達(dá)峰值后,試樣發(fā)生破壞,應(yīng)力-應(yīng)變曲線陡降,應(yīng)力值近乎垂直于橫向坐標(biāo)軸發(fā)生跌落,而灰?guī)r試樣脆性較強(qiáng)導(dǎo)致破壞在瞬間產(chǎn)生,部分試樣飛濺,所以無明顯的峰后曲線。

圖4 灰?guī)r試樣典型拉應(yīng)力-應(yīng)變曲線Fig.4 Typical tensile stress-strain curves of limestone samples
對(duì)于含層理灰?guī)r,采用宮鳳強(qiáng)等[18]推導(dǎo)的公式計(jì)算拉伸模量:
(2)
式中:Pt為破壞荷載,kN;Δut為最終拉伸長度,mm。
2.2 抗拉力學(xué)參數(shù)各向異性分析
對(duì)不同層理傾角灰?guī)r的巴西劈裂試驗(yàn)結(jié)果進(jìn)行處理,得到每組試樣抗拉強(qiáng)度與拉伸模量平均值,并依據(jù)結(jié)果計(jì)算出每組試樣泊松比,繪制巖樣力學(xué)參數(shù)與各層理傾角之間的關(guān)系曲線,如圖5所示。
由圖5(a)對(duì)比分析可知,隨著層理傾角的增大,巖石試樣抗拉強(qiáng)度與拉伸模量整體呈現(xiàn)下降趨勢,其中拉伸模量在30°~60°范圍內(nèi)隨層理傾角的增加曲線斜率由小變大,而抗拉強(qiáng)度的曲線斜率則反之。如圖5(b)所示,泊松比整體則隨層理傾角的增大呈上升趨勢,在90°時(shí)最大,為0.259;峰值應(yīng)變則在層理傾角為15°時(shí)達(dá)到峰值,為0.278,之后隨傾角的繼續(xù)增大呈減小的趨勢,在90°時(shí)最小,為0.178。
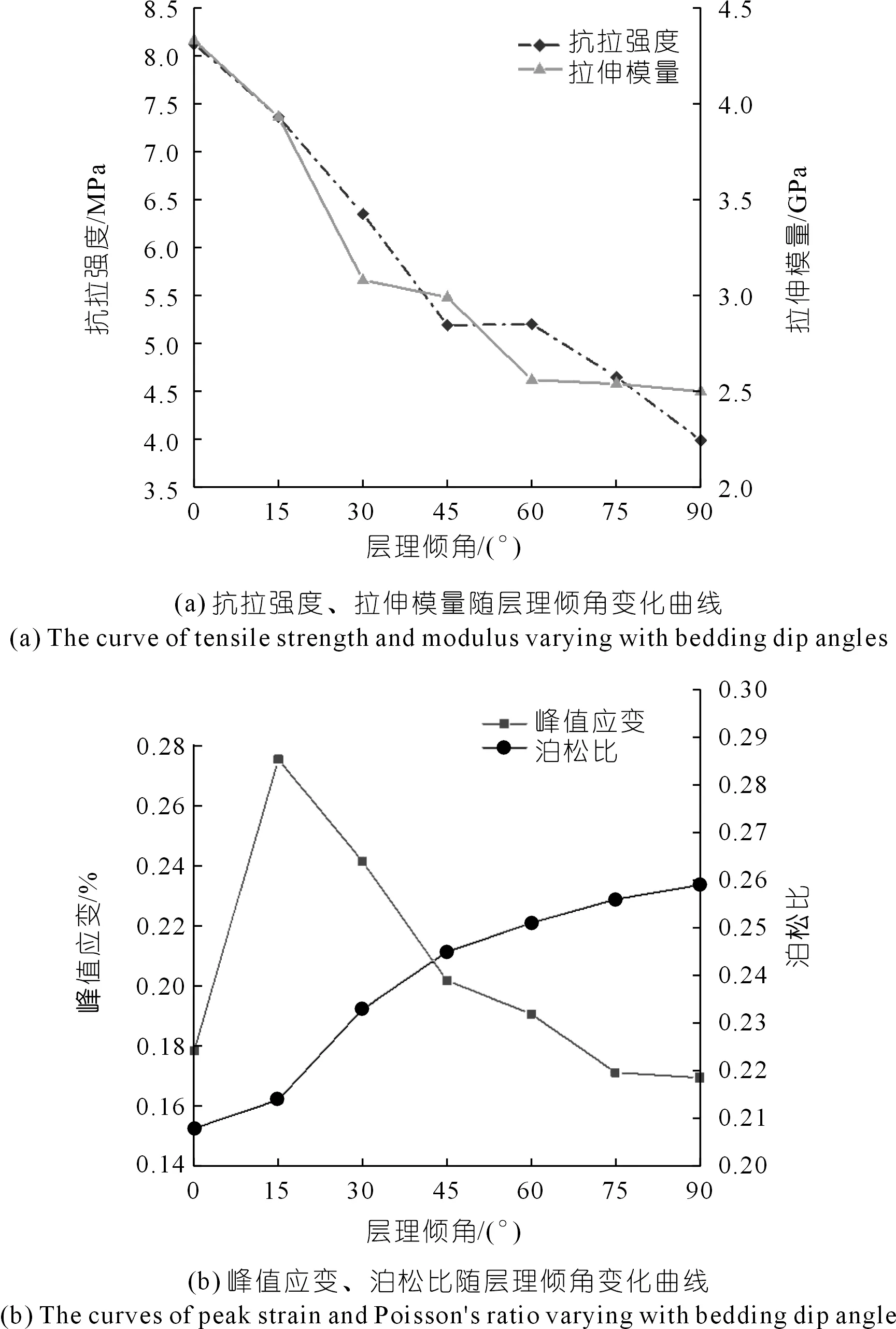
圖5 典型灰?guī)r試樣力學(xué)參數(shù)隨層理傾角變化曲線Fig.5 Curves of mechanical parameters varying with bedding dip angle
為了表征層理傾角對(duì)各力學(xué)參數(shù)各向異性影響的程度,引入各向異性度參數(shù)α(θ),表示不同層理傾角灰?guī)r力學(xué)參數(shù)與水平層理(θ=0)力學(xué)參數(shù)對(duì)比的降低幅度,即:
(3)
式中:ζ(θ)為不同層理傾角的力學(xué)參數(shù),如抗拉強(qiáng)度、拉伸模量等;ζ(0)為層理傾角為0時(shí)的力學(xué)參數(shù)。
α(θ)越大,表明巖樣力學(xué)參數(shù)受層理傾角影響越大,各向異性特征、層理結(jié)構(gòu)效應(yīng)越明顯。按照式(3)計(jì)算,不同層理傾角灰?guī)r的力學(xué)參數(shù)各向異性度變化曲線如圖6所示。
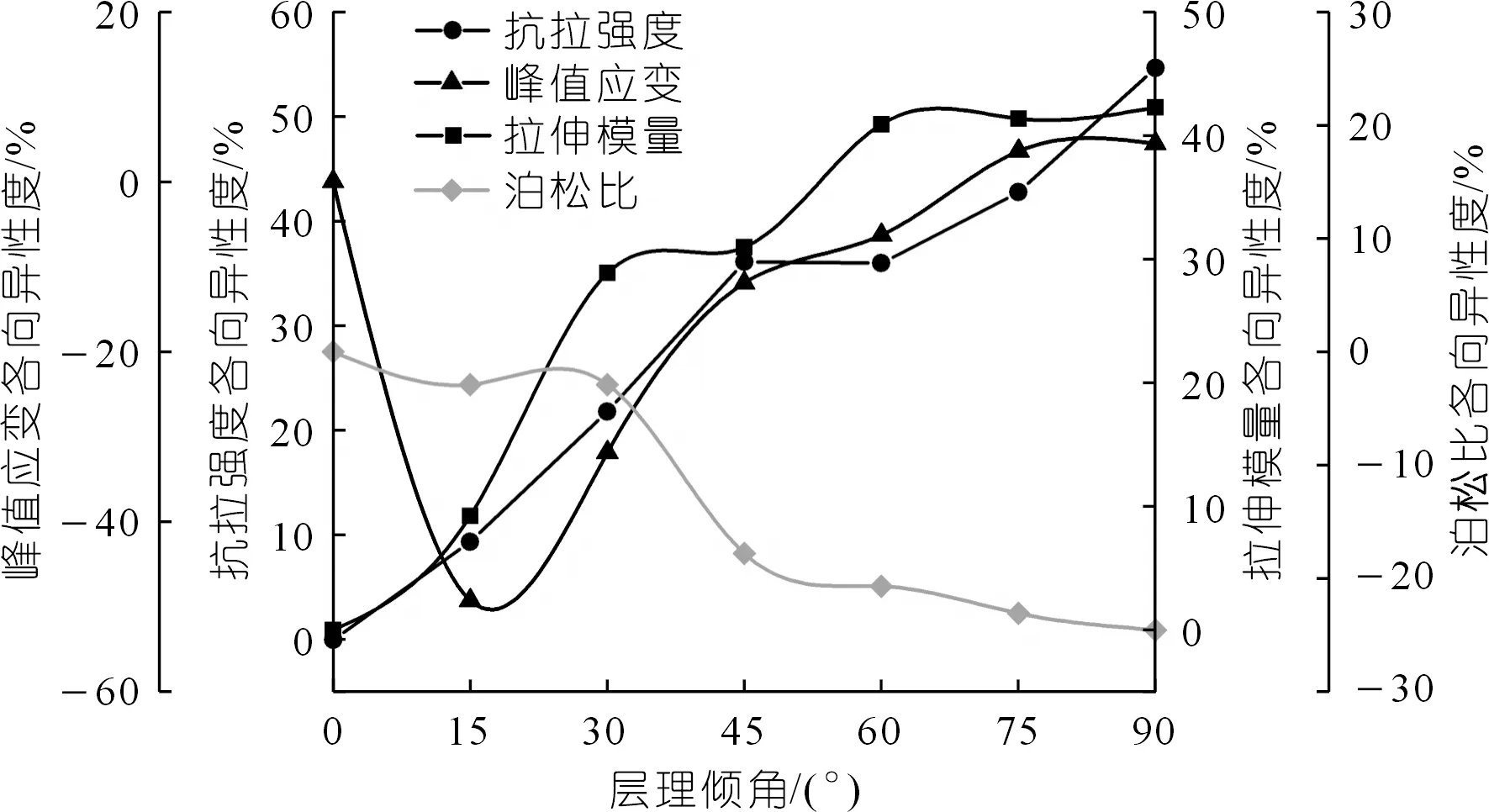
圖6 力學(xué)參數(shù)各向異性度曲線Fig.6 Curves of anisotropic mechanical parameters
從圖6中可以觀察到:隨著層理傾角的增加,抗拉強(qiáng)度和拉伸模量各向異性度曲線逐漸上升,在90°達(dá)到最大,相對(duì)于0°,增量分別約為55%,42%;泊松比各向異性度曲線隨著層理傾角增大呈負(fù)增長趨勢,也在90°時(shí)達(dá)到最大,相對(duì)于0°,增量約為25%;而峰值應(yīng)變各向異性度(絕對(duì)值)在層理傾角為15°時(shí)達(dá)到最大50%,隨后逐漸減小。這表明層理傾角對(duì)各個(gè)力學(xué)指標(biāo)均有影響,其中對(duì)抗拉強(qiáng)度和拉伸模量影響最大。
3 宏-細(xì)觀破壞形式及機(jī)制分析
3.1 宏觀破壞形態(tài)各向異性
將不同層理傾角的典型試樣加載過程中形成的宏觀裂隙進(jìn)行統(tǒng)計(jì)與素描,如圖7所示。從裂隙整體形態(tài)來看,破裂形態(tài)以張拉為主,部分出現(xiàn)沿層理剪切,主裂縫擴(kuò)展方向與試件所受最大主應(yīng)力方向一致。當(dāng)層理傾角為0時(shí),應(yīng)力垂直于層理方向,抑制了試樣沿層理方向滑移破壞的發(fā)生,主裂縫受到拉應(yīng)力作用穿過圓盤中心向兩端延伸,最終貫通形成垂直于層理方向的“直線”狀裂縫,為劈裂破壞,并且由于加載兩端產(chǎn)生應(yīng)力集中,所以加載點(diǎn)附近的巖樣出現(xiàn)次生裂縫,部分巖體碎屑掉落。此時(shí)測得的抗拉強(qiáng)度可以認(rèn)為是灰?guī)r基質(zhì)體的抗拉強(qiáng)度,因此θ=0°時(shí)的抗拉強(qiáng)度值為最大值。當(dāng)層理傾角θ=15°~30°時(shí),裂縫呈“月牙形”,即巖石樣品中間的裂縫向側(cè)面凸出。這是因?yàn)殡S著層理傾角逐漸增大,雖然主裂縫仍沿加載點(diǎn)起裂,以張拉破壞為主,但因受到薄弱層理面與礦物成分的影響,局部有剪切破壞產(chǎn)生,這也導(dǎo)致裂縫偏離圓盤中心擴(kuò)展,且有沿層理方向發(fā)展的趨勢。當(dāng)層理傾角θ=45°~60°時(shí),主裂縫沿弱面層理方向剪切型直線擴(kuò)展,在圓盤中心位置有局部次生張拉破壞。當(dāng)層理傾角θ=60°~75°時(shí),裂縫擴(kuò)展方向愈加接近于層理弱面,這會(huì)導(dǎo)致抗拉強(qiáng)度進(jìn)一步降低。當(dāng)θ=90°時(shí),雖然加載方向與層理面方向一致,但是加載點(diǎn)處無臨空剪出口,試樣沿層理弱面發(fā)生張拉破壞,此時(shí)所測抗拉強(qiáng)度本質(zhì)是層理弱面的抗拉強(qiáng)度,故此時(shí)的抗拉強(qiáng)度最小。
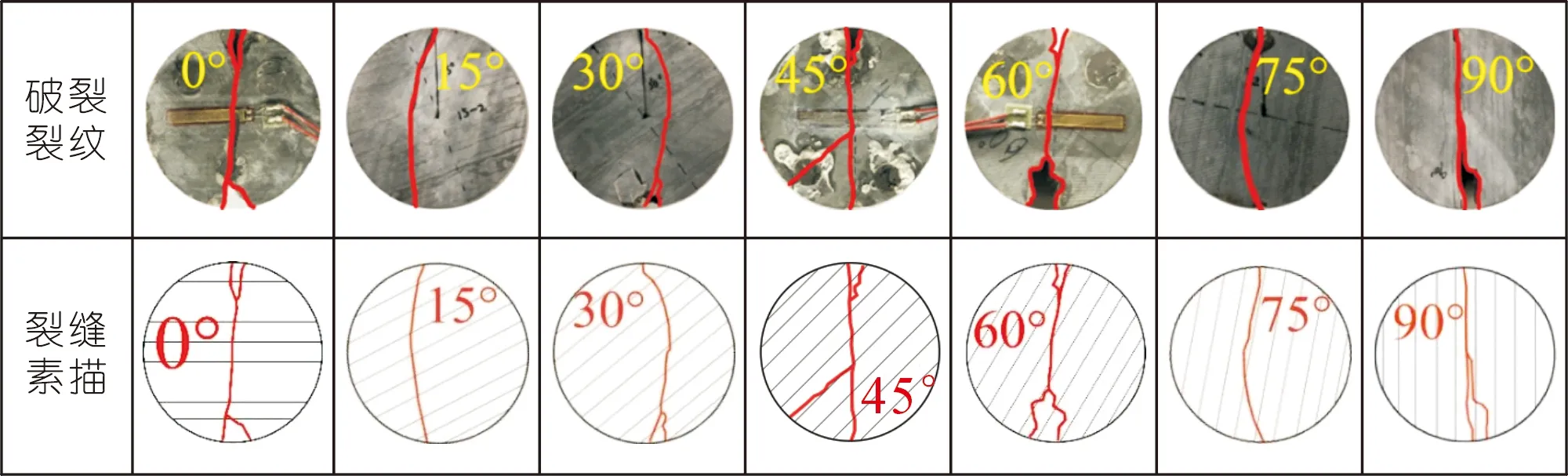
圖7 巖石破壞裂紋擴(kuò)展圖Fig.7 Crack propagation diagram of rock failure
3.2 破裂面細(xì)觀特征各向異性
將0,15°,30°,45°,60°,75°,90°等7種傾角的灰?guī)r進(jìn)行巴西劈裂試驗(yàn)后,取其正、反典型破裂面進(jìn)行高精度三維掃描,獲得7組點(diǎn)云數(shù)據(jù),并用Geomagic系列軟件對(duì)掃描面進(jìn)行平滑、降噪與封裝,提取坐標(biāo)并導(dǎo)入Surfer 12中進(jìn)行處理,生成的不同層理傾角灰?guī)r正、反破裂面三維數(shù)字圖像如圖8所示。

圖8 不同傾角典型巖樣破裂示意Fig.8 Schematic diagram of crack plane with different dip angle
當(dāng)層理傾角θ=0°時(shí),因加載點(diǎn)處出現(xiàn)小范圍的應(yīng)力集中而導(dǎo)致試樣發(fā)生局部到整體的張拉破壞,破裂面受力邊緣處比中間略顯粗糙。θ=15°~30°時(shí),巖樣發(fā)生部分剪切破壞,破裂面較θ=0°時(shí)平滑,正反兩塊巖樣破裂面凹凸起伏基本吻合,沿中心線部分巖體高于兩側(cè)巖體,這是由于巖樣受力范圍較小,先沿加載中心線方向發(fā)生張拉破壞,隨后再向兩側(cè)沿薄弱結(jié)構(gòu)面發(fā)生剪切擴(kuò)展,巖樣剖面呈“月牙形”。層理傾角θ=45°時(shí),破裂面粗糙,并且正反破裂面吻合度較低,起伏程度及凹凸位置均不相同。如反向破裂面右掃描圖所示,破裂面下緣呈臺(tái)階狀,中部破裂面較為破碎,試驗(yàn)后可觀察到較多巖石碎塊從巖樣上掉落。分析原因是由于此時(shí)發(fā)生的破壞不僅是層理面與灰?guī)r基質(zhì)體的拉伸-剪切破壞,還存在裂縫在發(fā)展過程中因局部應(yīng)力產(chǎn)生的二次張拉破壞,多種破壞同時(shí)作用導(dǎo)致巖樣呈破碎狀。當(dāng)層理傾角θ=60°~75°時(shí),受到剪切-拉伸作用的影響,巖樣剖面呈“弧形”,且如正反破裂面掃描圖所示,因?yàn)閷永砻孀鳛閹r體的薄弱結(jié)構(gòu)面,黏聚力較低,所以當(dāng)破壞平行于層理面產(chǎn)生時(shí),破裂面較為光滑。層理傾角θ=90°時(shí),加載方向與層理面方向平行,裂縫沿最薄弱層理面產(chǎn)生張拉破壞,受層理面內(nèi)充填礦物成分影響,破裂面又變粗糙。
3.3 破裂面結(jié)構(gòu)量化參數(shù)各向異性
3.3.1節(jié)理線粗糙度系數(shù)
Barton[19]在1973年首次提出節(jié)理粗糙度系數(shù)JRC的概念后,相關(guān)學(xué)者通過大量試驗(yàn)與研究給出了10條典型節(jié)理輪廓線,根據(jù)結(jié)構(gòu)面粗糙程度將JRC值定義在10~20數(shù)值范圍內(nèi),此方法在工程實(shí)踐中得到了廣泛應(yīng)用。但由于此方法是基于人工觀察對(duì)粗糙度進(jìn)行的大致估計(jì),受主觀性影響較大,故采用Gentier等[20]提出的裂隙面粗糙度的經(jīng)驗(yàn)?zāi)P停ㄟ^建立投影面積與實(shí)際面積的聯(lián)系,對(duì)不同層理傾角灰?guī)r破裂面線粗糙度進(jìn)行計(jì)算。本次試驗(yàn)定義破裂面切口面積為截面面積,又因試驗(yàn)采用了統(tǒng)一直徑為50 mm、厚度為25 mm的試樣,故定義標(biāo)準(zhǔn)截面面積1 250 mm2。通過三維掃描儀獲取點(diǎn)云數(shù)據(jù),并對(duì)不同層理傾角下巖樣斷裂面面積進(jìn)行數(shù)值化處理后獲得不同層理傾角破裂面實(shí)際表面積,以式(4)進(jìn)行計(jì)算:
(4)
式中:RL為裂隙的線粗糙度,無量綱,與破裂面粗糙程度呈正相關(guān);RA為粗糙裂隙面實(shí)際面積與裂隙面投影面積之比。
3.3.2粗糙度分形維數(shù)
自Mandelbrot將分形幾何運(yùn)用于巖體結(jié)構(gòu)面粗糙度系數(shù)研究以來[21],分形理論逐漸成為處理復(fù)雜系統(tǒng)的有力工具,而盒維數(shù)法在粗糙度分形理論中有著廣泛的應(yīng)用[22]。使用邊長為ε的立方體盒子依次覆蓋試樣破裂面表面,N(ε)為覆蓋試樣破裂面所需要的邊長為ε的立方體個(gè)數(shù),得到:
N=ε-D
(5)
式(5)等號(hào)兩邊取對(duì)數(shù),可得:
lgN=-Dlgε
(6)
取不同尺寸的ε,其對(duì)應(yīng)的N(ε)是恒定的,將兩者用最小二乘法擬合成直線,直線斜率的相反數(shù)即為該破裂面粗糙度盒維數(shù),即:
(7)
式中:ε為立方體的邊長;N(ε)為破裂面被覆蓋所需的邊長為ε的立方體個(gè)數(shù);DB為破裂面粗糙度盒維數(shù)。
試樣破裂面越粗糙,起伏程度越大,覆蓋破裂面需要的盒子數(shù)就越多,所得粗糙度盒維數(shù)就越大。在巴西劈裂試驗(yàn)條件下,選取不同層理傾角灰?guī)r破裂面進(jìn)行三維激光掃描,通過MATLAB編寫盒維數(shù)算法對(duì)掃描數(shù)據(jù)進(jìn)行處理,使破裂面三維成像并置于一平面上,將平面用網(wǎng)格進(jìn)行劃分,然后用不同邊長εi的立方體盒子去覆蓋三維破裂面,程序中將盒子尺寸設(shè)置為2n(mm)依次進(jìn)行覆蓋,覆蓋過程如圖9所示
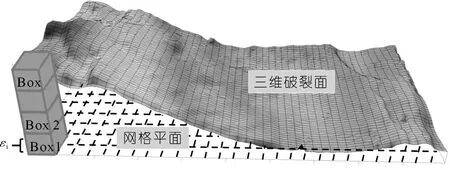
圖9 盒維數(shù)計(jì)算示意Fig.9 Schematic diagram of box dimension calculation
計(jì)算不同層理傾角灰?guī)r線粗糙度與盒維數(shù)值結(jié)果如表1所列,繪制結(jié)構(gòu)面量化參數(shù)各向異性曲線如圖10所示,兩者隨著層理傾角的增大變化趨勢基本一致。
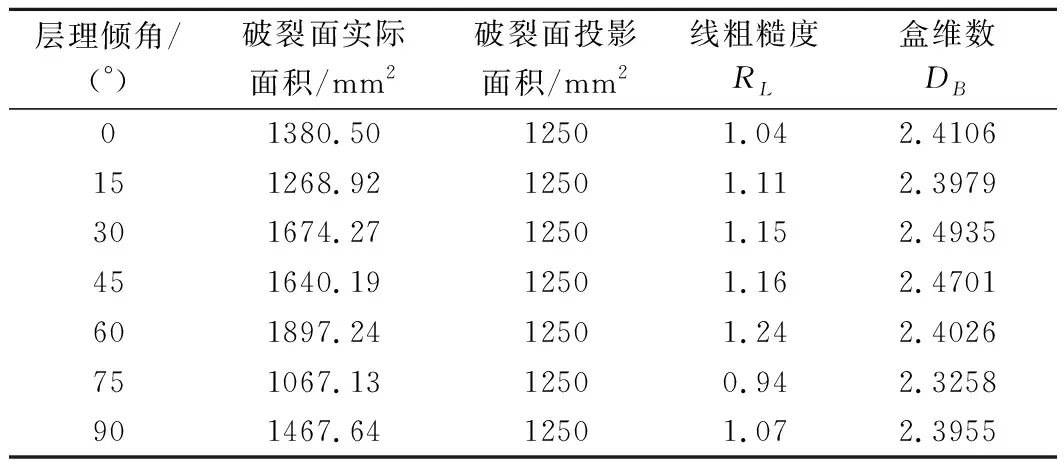
表1 不同層理傾角灰?guī)r結(jié)構(gòu)面量化參數(shù)
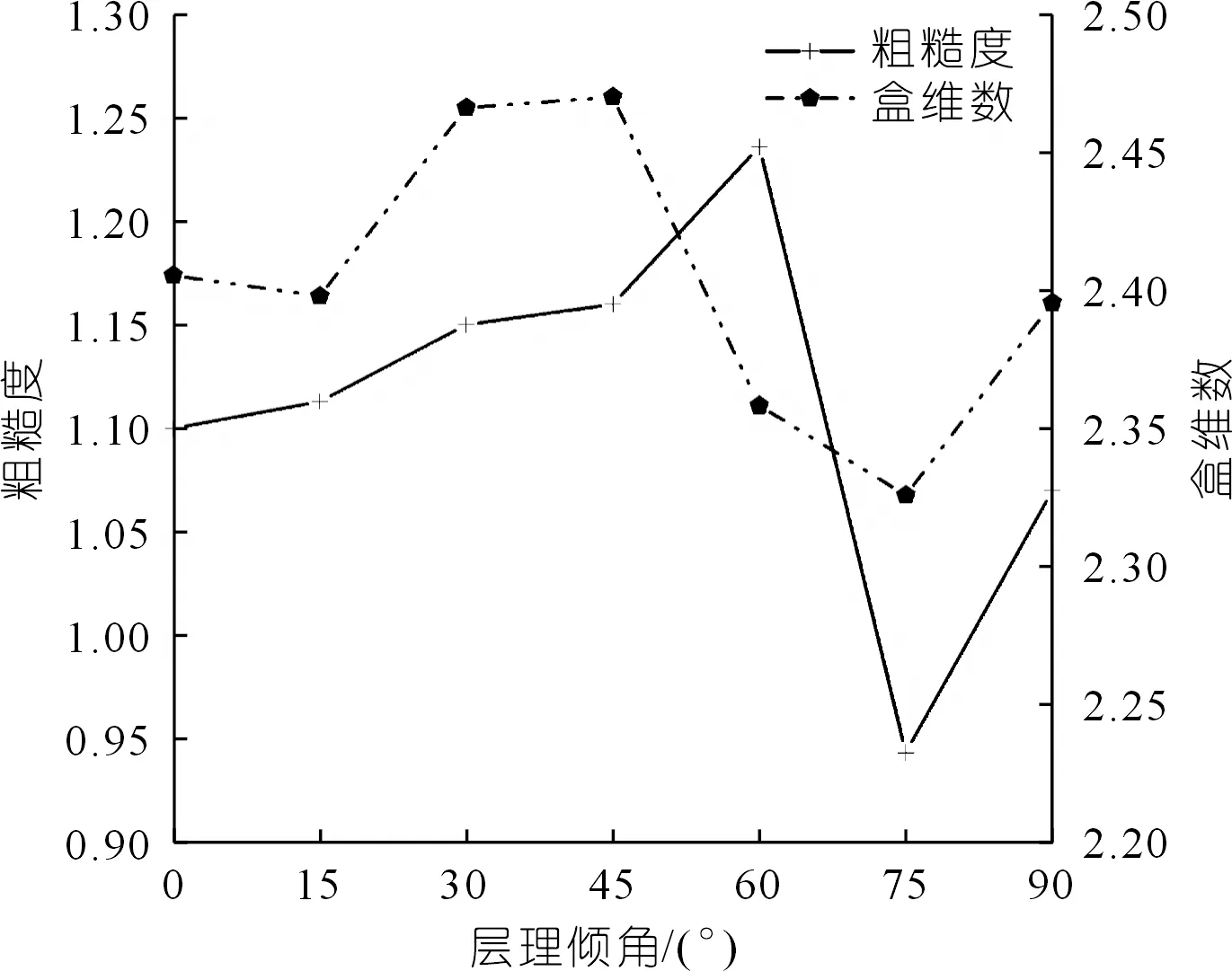
圖10 結(jié)構(gòu)面量化參數(shù)各向異性系數(shù)對(duì)比曲線Fig.10 Comparison curve of anisotropy coefficient of quantitative parameters of discontinuity
層理傾角θ=0°時(shí)的結(jié)構(gòu)面量化參數(shù)均大于層理傾角θ=90°時(shí)的對(duì)應(yīng)參數(shù),即層理傾角θ=90°的破裂面較層理傾角θ=0°時(shí)的破裂面光滑。這是因?yàn)楫?dāng)層理傾角θ=0°時(shí),試樣裂縫貫通灰?guī)r基質(zhì)體,拉應(yīng)力由灰?guī)r基質(zhì)體承擔(dān),而θ=90°時(shí)試樣是沿層理弱面發(fā)生張拉破壞,因?qū)永砣趺鎻?qiáng)度較小發(fā)生張拉破壞時(shí)裂縫擴(kuò)展所受阻力更小,破裂面更光滑。就盒維數(shù)隨層理傾角變化曲線而言,DB(θ=0°)略大于DB(θ=15°),這是因?yàn)棣?15°時(shí)的巖樣破壞模式開始受到層理傾角的影響,開始有局部的剪切破壞產(chǎn)生,破裂面的部分凸起體被剪切磨平,粗糙度開始降低。當(dāng)層理傾角θ=30°~45°時(shí),由加載點(diǎn)施加的軸向應(yīng)力分解為沿層理面的剪應(yīng)力與沿加載中心線的法向應(yīng)力,雖然此時(shí)仍以拉伸破壞為主導(dǎo)并伴隨局部的剪切破壞,但隨著破壞的進(jìn)一步發(fā)展,應(yīng)力分配不斷變化,破裂面變化情況復(fù)雜,破裂面如洼地等起伏形態(tài)增多,所需要覆蓋破裂面的盒子數(shù)變多,DB變大。當(dāng)層理傾角θ=60°~75°時(shí),隨著層理面逐漸傾向于加載中心線,沿層理面剪應(yīng)力逐漸增大,裂縫路徑逐漸沿層理方向擴(kuò)展,大量破裂面凸起體逐漸從被剪短磨損進(jìn)入剪切滑移階段,破裂面光滑部分增多,盒維數(shù)減少。當(dāng)層理傾角θ=90°時(shí)發(fā)生層理面張拉破壞,此時(shí)破裂面的粗糙程度又有所增大,因此曲線又反向增大,這是由層理弱面礦物成分等因素決定的。
整體而言,盒維數(shù)DB的變化趨勢與宏-細(xì)觀破裂特征較符合,隨著層理傾角的增大,盒維數(shù)在θ=30°~45°達(dá)到峰值后逐漸減小,這說明拉-剪復(fù)合作用下破裂面破壞狀況較復(fù)雜,隨著裂縫路徑逐漸偏向?qū)永韮A角,剪切破壞起主導(dǎo)作用,破裂面逐漸變得平滑。線粗糙度RL整體走勢雖與盒維數(shù)DB相近,隨層理傾角的變化呈先增大后減小的趨勢,但相較于盒維數(shù)DB在θ=45°達(dá)到峰值,線粗糙度RL則于θ=75°時(shí)達(dá)到峰值,并且在層理傾角θ=0°~45°時(shí),RL逐步增大,并未如盒維數(shù)DB一般在θ=15°出現(xiàn)小幅減小的情況。筆者認(rèn)為這是由于θ=15°~30°,θ=45°~70°時(shí),巖樣剖面呈“弧形”或“月牙形”,由線粗糙度定義可知,破裂面曲度會(huì)對(duì)線粗糙度值產(chǎn)生一定影響,因此發(fā)現(xiàn)相較于線粗糙度,盒維數(shù)能更好地量化反映灰?guī)r破裂面粗糙程度隨層理傾角的變化規(guī)律,可為研究破裂面之間的差異特征提供有效手段。
4 結(jié) 論
針對(duì)不同層理傾角灰?guī)r開展了巴西劈裂試驗(yàn)研究,對(duì)層理灰?guī)r力學(xué)參數(shù)各向異性特征進(jìn)行了比較分析,利用三維掃描技術(shù)對(duì)宏觀破裂形態(tài)與細(xì)觀破裂特征進(jìn)行了總結(jié)與量化統(tǒng)計(jì),得到以下主要結(jié)論:
(1) 層理灰?guī)r抗拉力學(xué)特性具有明顯的各向異性,通過各向異性度比較發(fā)現(xiàn),抗拉強(qiáng)度與拉伸模量受層理傾角影響較強(qiáng)烈,兩者隨層理傾角的增大呈減小的趨勢。當(dāng)θ=0時(shí),抗拉強(qiáng)度與拉伸模量最大,分別為8.12 MPa和4.33 GPa,這是灰?guī)r基質(zhì)體的力學(xué)參數(shù)。當(dāng)θ=90°時(shí),抗拉強(qiáng)度與拉伸模量最小,分別為3.99 MPa和2.50 GPa,這是灰?guī)r層理弱面的力學(xué)參數(shù)。
(2) 灰?guī)r的宏觀破壞裂縫可分為3種典型形態(tài):直線型、月牙形、弧形。當(dāng)層理傾角θ=0,90°時(shí)宏觀裂縫均呈“直線型”的張拉破壞;當(dāng)層理傾角15°≤θ≤30°時(shí),宏觀裂縫呈“月牙形”,巖樣中間的裂縫向一側(cè)突出,此時(shí)有局部剪切破壞產(chǎn)生;當(dāng)層理傾角45°≤θ≤75°時(shí),宏觀裂縫呈“弧形”,屬于拉-剪復(fù)合破壞形態(tài),次生裂縫發(fā)育豐富。
(3) 通過三維激光掃描技術(shù)對(duì)破裂面進(jìn)行數(shù)字化處理,采用RL,DB兩種結(jié)構(gòu)面量化參數(shù)評(píng)價(jià)破裂面粗糙程度,發(fā)現(xiàn)層狀巖體破裂面粗糙程度也具有明顯的各向異性:在θ=0°~90°區(qū)間內(nèi),粗糙程度整體呈先增大后減小的趨勢,破裂面張拉作用越強(qiáng),起伏粗糙度越大,剪切作用越強(qiáng),起伏粗糙度越低。而通過比較結(jié)構(gòu)面量化參數(shù)RL,DB發(fā)現(xiàn),盒維數(shù)DB各向異性特征較明顯,能較好反映不同層理傾角破裂面之間的差異特征,線粗糙度則受試樣剖面曲度因素影響較大。
- 人民長江的其它文章
- 石油鉆井工程風(fēng)險(xiǎn)因素分析與控制方法研究
——評(píng)《石油鉆井風(fēng)險(xiǎn)管理技術(shù)研究與實(shí)踐》 - 異構(gòu)環(huán)境下大數(shù)據(jù)傳輸能耗優(yōu)化的方法
——評(píng)《大數(shù)據(jù)處理平臺(tái)能耗優(yōu)化方法的研究》 - 小水電生態(tài)修復(fù)思考
- 生態(tài)流量泄放對(duì)無調(diào)節(jié)引水式電站發(fā)電量影響分析
- 地鐵施工安全事故風(fēng)險(xiǎn)評(píng)價(jià)
- 地球物理技術(shù)在巖溶水庫滲漏通道識(shí)別中的應(yīng)用

