基于SSA-LSTM的混凝土拱壩變形預測模型

孔慶梅,喬海山,費新鋒,武志剛,葛佳豪

(1.國家電投集團青海黃河電力技術有限責任公司,西寧 810008；2.西安理工大學水利水電學院,西安 710048)

0 前 言

水庫大壩在運行過程中不僅受各種動、靜循環荷載和地震、滑坡等災害的作用，還要受混凝土自身材料性質改變和物理、化學作用導致的侵蝕與腐蝕，由此導致壩體在運行期不同階段安全性態發生改變[1]。大壩失事后果嚴重，及時準確了解大壩安全性態，保證其穩定運行十分重要[2]。大壩變形能夠客觀地判斷出工程是否處于安全性態，對大壩變形過程中的實測資料進行分析，以此來建立誤差較小的安全監控模型是檢驗工程是否安全的主要手段之一[3-5]。工程應用中針對具有復雜非線性特點的大壩變形監測數據，已經發展出了傳統數學統計模型、確定性模型、組合模型及混合模型用于大壩的安全監控[6]。其中確定性模型和統計模型應用較廣，但是由于壩體自身材料特性和運行環境均具有一定的不確定性，導致模型比較復雜；傳統統計模型原理清楚且構造簡單，但預測效果一般[6]。

近年來，相關學者在大壩變形分析與變形預測方面作了開展了深入的研究。胡德秀[7]提出了基于穩健估計極限學習機ELM的大壩變形安全監控模型，并通過實例驗證了模型的抗粗差性和對大壩安全監測非線性的適用性。對于環境影響因子之間的相關性問題，陳詩怡[6]采用Copula函數非線性相關檢驗確定最優因子集，結合隨機森林算法建立大壩安全監控模型。宋洋[8]利用自適應噪聲完全集合經驗模態分解(EMD)將原始變形數據分解為頻率不同、復雜度差異明顯的一組固有模態函數，并在此基礎上使用排列熵方法進行合并重組，對若干重組序列分別構建LSTM模型進行預測，將預測結果相加得到最終變形預測值。馬廣臣[9]利用動態權重粒子群算法對自適應模糊神經網絡中模糊層的適應度值進行參數尋優，形成可以尋找最優適應度值的自適應模糊神經網絡。李其峰[5]結合貝葉斯優化算法優化門控制循環單元(GRU)超參數，建立大壩安全監控模型。王麗蓉[10]等融合動態時間規整算法和卷積長短時記憶網絡，構建了大壩安全監測整體信息聯合監控模型，該模型具有提取測點最新相關性信息和處理時序數據的能力。

目前，基于智能算法的大壩安全監控模型已經在大壩安全性態分析中發揮了重要作用，但很多方法還是存在收斂速度慢和穩定性差等問題。

隨著計算科學技術的不斷發展和工程應用，很多工程問題都可以使用群智能優化方法解決[11]。根據具體自然現象衍生出了如粒子群優化算法[12]、人工蜂群算法[13]、細菌覓食算法[14]和螢火蟲算法[15]等群智能優化算法，并得到了較廣泛的工程應用。但隨著科學問題、工程問題越來越復雜，很多群智能優化算法還是存在計算時間過長及易陷入局部最優等的不足。在簡化了麻雀個體的覓食行為、反捕食行為的基礎上，薛建凱[16]等于2020年提出了麻雀搜索算法(Sparrow Search Algorithm, SSA)，其具有求解精度高、收斂快、穩定性好等優點[17]。

本文將具有全局優化能力的麻雀優化算法SSA引入深度學習中的長短期記憶神經網絡LSTM中，智能優化神經網絡超參數，以減少由于人工設定參數而造成過擬合的問題，提高構建模型的準確度和收斂速度。在對比大壩安全監控模型的同時，對受大壩異常情況影響的不同測點進行對比分析。

1 麻雀優化算法

SSA算法[16]預設發現者與加入者這兩種麻雀。算法運行時，當發現者發現食物充足的區域，加入者就會受到召喚并向該區域移動，因此麻雀所在區域的食物是否充足決定了麻雀個體能量的高低。另外，為了避免陷入局部最優，在種群中按設定比例隨機選取部分麻雀作為預警者。當迭代計算滿足一定條件時，預警者將會選擇相應的更新方式進行額外移動。

對于發現者：

(1)

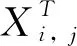
對于加入者：

(2)

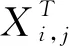
對于預警者：

(3)

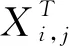
2 長短期記憶神經網絡LSTM

1997年，由Hochreiter[18]等改進了循環神經網絡(Recurrent Neural Network，RNN)中的隱藏層，提出了長短期記憶神經網絡(Long Short-Term Memory，LSTM)，且在RNN每個記憶神經元上增加了一個記憶單元。同時其3個門結構(即輸入門、遺忘門和輸出門)選擇性記憶梯度下降時誤差函數反饋的修正參數，以保留有價值信息或丟棄過時信息。LSTM通過引入可控自循環有效避免了長時間序列學習過程中經常遇到的梯度消失或梯度爆炸問題，適用于處理時序延遲和間隔冗長的任務[19]。其結構如圖1所示[5]。

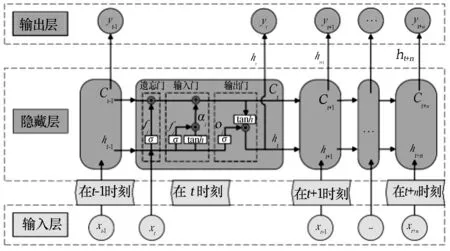
圖1 LSTM原理及結構

LSTM神經網絡的計算公式如下：

(4)

公式(4)中:it、ft、ct、ot分別表示輸入門、遺忘門、更新后的細胞狀態及輸出門；xt為輸入信息；ht為獲取的輸出信息；W為權重系數；bi、bf、bc、bo為偏置量;*表示哈達瑪積符號；下標t表示累計時長，d。

輸入門用來更新信息；遺忘門決定從上一個狀態中丟棄信息或保留信息；輸出門控制計算后的狀態并輸出。LSTM通過門結構使之前的輸入信息能夠繼續向后傳播而不消失，從而具有較好的長、短時記憶能力，在預測中又有較好的擬合效果，能很好地進行變形時間序列的預測分析[8]。

3 混凝土拱壩變形預測模型構建

建立基于麻雀搜索算法(SSA)的長短期記憶神經網絡(LSTM)混凝土拱壩變形預測模型，其主要有4個步驟:① 數據預處理；② 模型超參數進行優化；③ 模型訓練與預測；④ 模型性能評價。

因為不同的環境量如水位、溫度、時效和效應量如位移、應力等監測項目具有不同的量綱，也會有不同的數量級[5]。為便于分析，淡化量綱和數量級對預測值的影響，對原始時間序列進行處理。本文通過公式(5)所示的方法對數據進行歸一化處理，將原始時間序列縮放到[0，1]區間。

(5)

公式(5)中：Xstd為歸一化后的時間序列；Xmin為原始時間序列的最小值；Xmax為原始時間序列的最大值。

然后選取具有代表性的壩頂測點徑向位移數據進行訓練。為提高模型的精度，將LSTM嵌入到麻雀優化算法中，對其超參數進行優化。搜索模型中最大迭代次數、初始學習率、隱藏單元個數共3個參數的最優化值，本文設定的搜索范圍分別為[100,500]、[0.0001,0.001]和[10,400]，miniBatchSize設置為128。將尋找到的最優超參數組合設定給LSTM，向其輸入訓練集的實測數據得到預測數據，對預測結果進行反歸一化處理，得到預測結果。

為驗證本文所提出模型的準確性和適用性，將SSA-LSTM模型的預測結果與BP神經網絡、極限學習機(ELM)和支持向量機(SVM)等傳統監控模型的預測結果進行對比分析。并通過其他測點的實測數據驗證該方法的適用性。綜上，基于SSA-LSTM的混凝土拱壩變形預測流程見圖2。

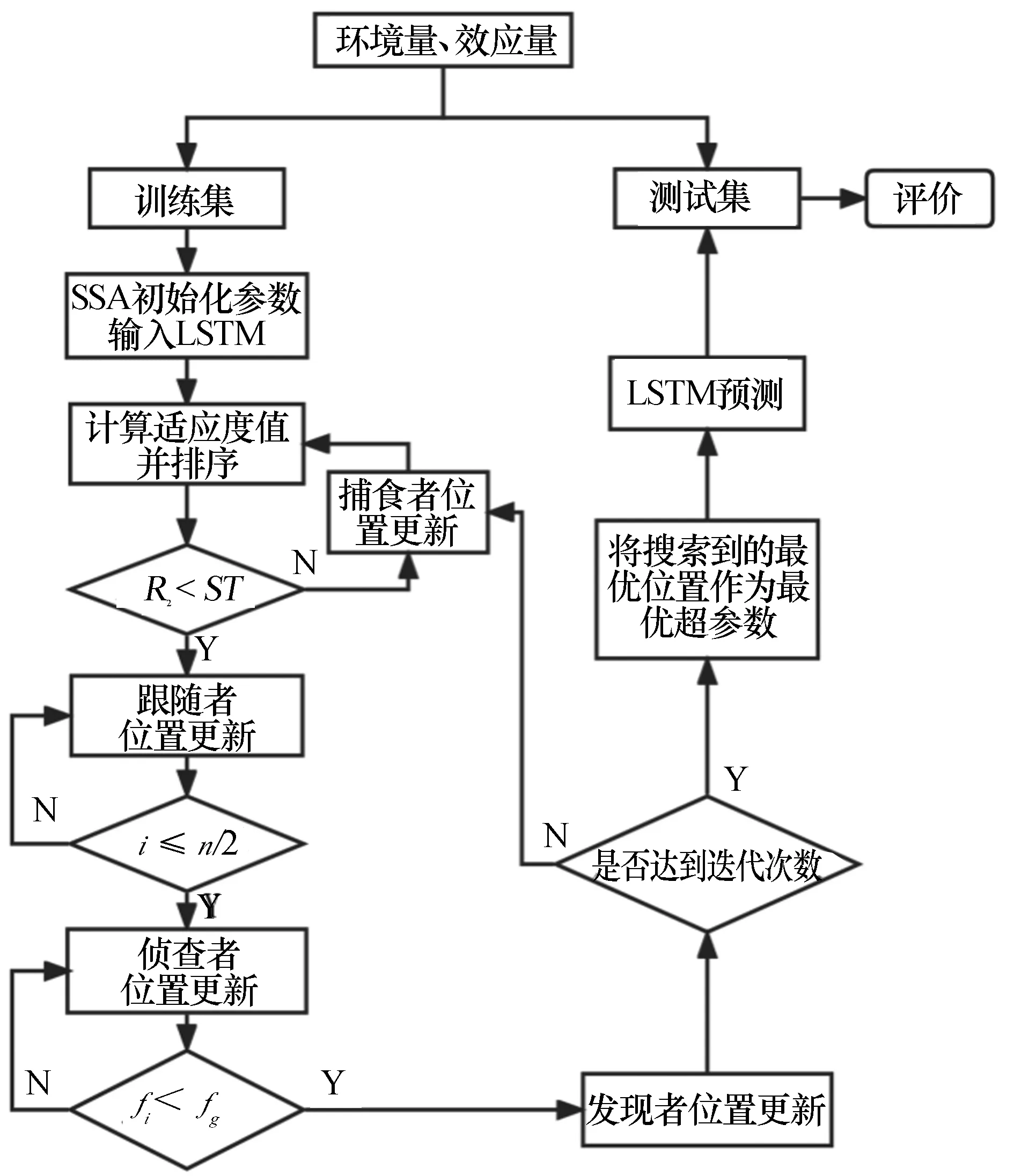
圖2 SSA-LSTM的混凝土拱壩變形預測流程

4 工程實例

將建立的LSTM模型應用在拉西瓦拱壩垂線監測的徑向位移成果中，以檢驗模型的有效性和魯棒性。

4.1 工程概況

拉西瓦水電站擋水建筑物為雙曲薄拱壩，最大壩高250 m，建基面高程2 210.00 m，壩頂高程2 460.00 m，壩頂中心線弧長466.63 m；兩岸拱座采用半徑向布置,如圖3。該拱壩的水位在2011年已經保持較高水位運行，2011—2013年間又逐漸上升，但上升幅度較小，2013年后則基本穩定。因此作為一個空間殼體結構，拉西瓦拱壩壩頂的徑向位移表現出了明顯的季節性波動。

圖3 拉西瓦拱壩

拉西瓦拱壩垂線監測布置見圖4。本文以壩頂PL2-1、PL4-1和PL5-1共3個測點的徑向位移實測數據為例，檢驗SSA-LSTM混凝土拱壩變形預測方法的精度和適用性，并與傳統監控模型進行性能對比。PL2-1、PL4-1和PL5-1測點的徑向位移實測數據見圖5。

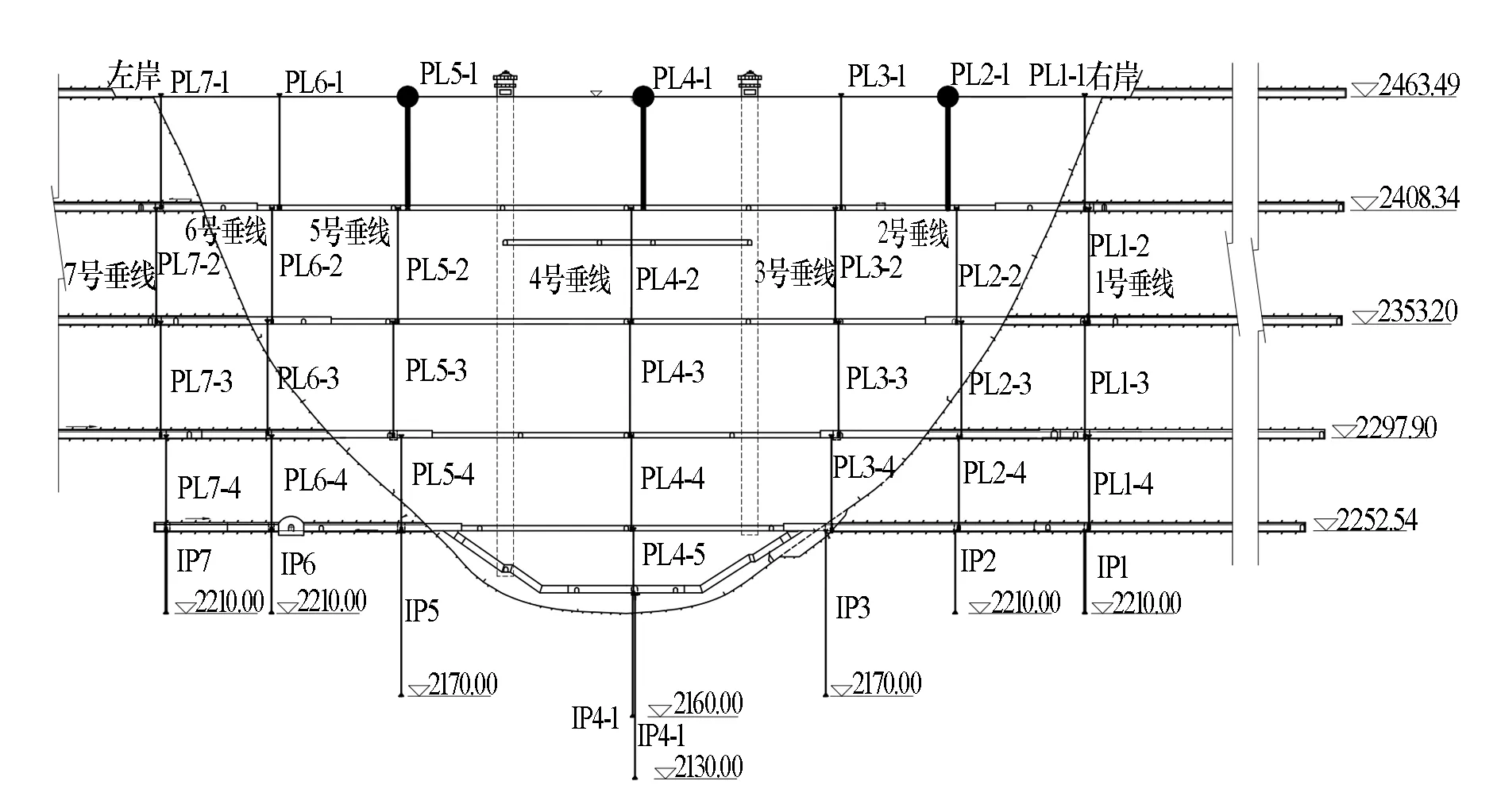
圖4 拉西瓦拱壩垂線監測布置 單位：m

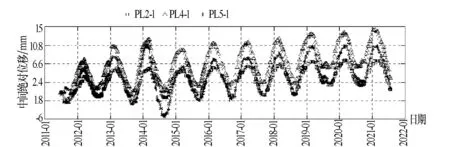
圖5 壩頂垂線PL2-1、PL4-1和PL5-1測點實測徑向絕對位移過程線

如圖5，由于2013年壩體下游面左岸壩段的保溫板失效，導致左岸壩段PL5-1和拱冠梁PL4-1測點在2013年底冬季、2014年夏季徑向位移變幅明顯增大，與失效前和修復后的徑向位移周期性規律明顯不同，而右岸壩段的PL2-1測點受影響較小，因此將這3個典型測點進行對比，以分析異常位移對監控模型的影響。

4.2 模型結構和參數

混凝土拱壩在服役期內主要受水壓力、溫度、時效等因素作用發生變形[20]。因此大壩的徑向位移δ為：

δ=δH+δT+δθ

(6)

公式(6)中：δH、δT、δθ分別為水壓、溫度和時效因子，具體公式如下：

(1) 水壓因子

(7)

(2) 溫度因子

(8)

(3) 時效因子

δθ=c1θ+c2ln(1+θ)

(9)

公式(9)中：時效因子主要包括線性函數θ和對數函數ln(1+θ)，以模擬拱壩運行初期的趨勢性變形。

以上述8項水壓因子、4項溫度因子和2項時效因子作為模型輸入，壩頂PL2-1、PL4-1和PL5-1測點徑向位移的實測數據作為輸出，分別應用SSA-LSTM模型和傳統的BP神經網絡、極限學習機(Extreme Learning Machine，ELM)、支持向量機(Support Vector Machine，SVM)進行訓練和預測，以進行對比研究。采用GA算法對SVM模型優化，得到最優懲戒因子系數為128，核函數參數為0.2；ELM采用默認傳遞函數Sigmoid，隱藏神經元數為15。數據樣本為2011—2021年間的共417個數據(一周一測)，各模型均指定85%數據用于訓練，15%的數據用于預測和驗證。

4.3 模型應用及評價

4.3.1評價指標

為了檢驗預測模型的性能，本文選取了4個參數作為評價指標來分析模型的預測精度，分別為平均絕對誤差(MAE)、絕對誤差百分比(MAPE)、均方根誤差(RMSE)和決定系數(R2)。其計算公式如下：

(10)

(11)

(12)

(13)

4.3.2模型訓練及性能評價

使用麻雀搜索算法對LSTM模型參數的尋優結果為：最大迭代次數Max_Epochs=500、初始學習率Initial_Learn_Rate=0.005、隱藏單元個數num_hidden_units=256。SVM核為徑向基函數；ELM采用默認傳遞函數SIGMOID，隱藏神經元數為15。不同模型在PL4-1測點的徑向位移的預測結果如圖6所示，3個測點采用不同模型的預測性能評價指標見表1。

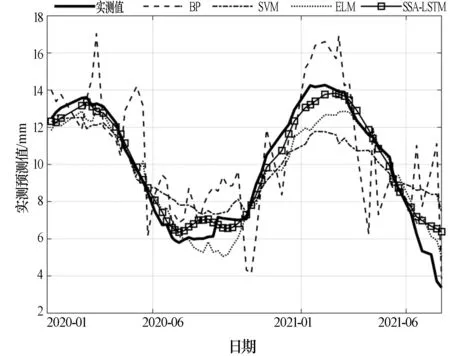
圖6 多個模型在PL4-1測點的預測結果與實測值

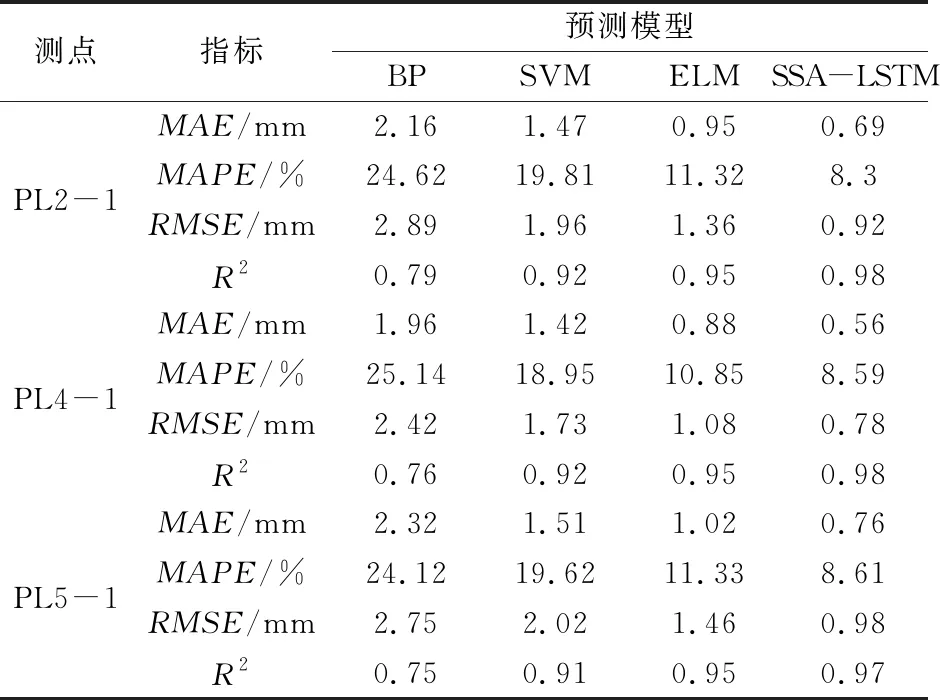
表1 PL2-1、PL4-1和PL5-1實測徑向位移多個模型預測性能指標

由圖6可知，PL2-1、PL4-1和PL5-1測點的徑向位移均具有明顯的周期性變化，同時還有較明顯的趨勢性變化。其中PL5-1受2013年保溫板失效的影響，其徑向位移在2014年變幅明顯變大，PL4-1和PL2-1受影響較小但仍有一定變化。

由圖6可知4種模型均能較好預測PL4-1測點的徑向位移規律，預測結果基本與實測值呈現相同的周期性規律。其中，BP神經網絡的預測結果較不穩定，波動較大；SVM模型預測結果的周期性變幅變明顯小于實測值；ELM模型預測效果較好，但周期性峰值、谷值對應的時間點明顯晚于實測值。SSA-LSTM模型的預測效果明顯好于其他模型，較好地體現了該測點的周期性變化，變幅預測也更為準確，在幾個對比方法中表現最優。

從預測值的評價指標來看，使用SSA-LSTM模型的預測評價指標均比其他模型要好而且更加突出：SSA-LSTM模型的平均絕對誤差、絕對誤差百分比、均方根誤差和復相關系數分別為0.56 mm、8.59%、0.78 mm和0.98，與其他對比模型相比明顯更優。從預測值評價指標復相關系數R2來看，相較于BP神經網絡、SVM和ELM方法的預測值，SSA-LSTM模型預測值的復相關系數分別提高了0.22、0.06和0.03，這表明SSA-LSTM模型所估的偏差范圍較小，相關性更強，擬合的精準度也較高；從平均絕對誤差、絕對誤差百分比和均方根誤差來看，SSA-LSTM預測的位移誤差相對其他方法均更低，說明該方法的預測值與實測值更加接近，預測效果更好。

對比不同測點預測結果的評價指標可以發現：采用不同方法對PL2-1和PL5-1兩個測點的預測效果整體上基本與PL4-1一致，不同方法的平均絕對誤差、絕對誤差百分比、均方根誤差和復相關系數4個評價指標均表現出了同樣的趨勢，且SSA-LSTM模型均明顯優于其他方法。但受大壩下游面保溫板失效導致的異常變形的影響，PL5-1測點的異常變幅在3個測點中最大，因此其預測效果相比PL4-1和PL2-1兩個測點較差，這也符合異常位移對預測模型的影響規律。

綜上所述，使用SSA-LSTM模型可以很好地預測混凝土拱壩非線性變形序列的優勢。相比于其他模型，基于SSA-LSTM的混凝土變形模型可以將深度學習在非線性時間序列預測方面的優點發揮出來，從而使預測結果更加準確。

5 結 論

本文將麻雀搜索算法和深度學習中的長短期記憶神經網絡結合，用于混凝土拱壩徑向位移變形監測分析中，構建了基于SSA-LSTM模型的混凝土拱壩變形預測方法。通過實例驗證了本模型是比較可靠且實用的，主要結論如下：

(1) 通過麻雀搜索算法優化LSTM模型中的最大迭代次數、初始學習率、隱藏單元個數3個參數，避免了人工設置參數帶來的不確定性，避免模型陷入局部最優，提高了模型的精度。

(2) 通過與BP神經網絡、SVM和ELM模型進行對比，充分證明了SSA-LSTM模型具有較強的預測能力，可用于大壩安全預警預報。

(3) 由于突發事件導致的大壩某測點發生異常位移，會導致大壩預測模型的精度出現一定程度的降低。

本文僅針對單個測點逐個進行回歸預測分析，但大壩是一個高度復雜的系統，具有較強的不確定性。因此，在開展多測點的變形預測研究時，有必要需要綜合考慮多個測點的變形協調關系，開展多測點的變形預測研究。