屏蔽室通風仿真設計研究

呂 芳， 姜建中， 貢毅超， 張 巖

（1.軍事科學院國防工程研究院， 北京 100000；2.中國電子科技集團公司第三十三研究所， 山西 太原 030032）

引言

屏蔽室通風設計是為了在散熱、通風與空氣調節中執行國家經濟政策，采用先進技術，合理利用資源和節約能源，保護環境，保證健康舒適的工作和生活環境[1-3]。

本次屏蔽室通風仿真設計根據總體要求，以某項目屏蔽室為研究對象，屏蔽室大小（長×寬×高）為6 500 mm×4 000 mm×3 000 mm，提出了五種較為常見的通風方式，通過研究各布置方式出風量的變化，為今后的工程應用提供設計依據。圖1 為該屏蔽室外觀。

圖1 屏蔽室外觀

1 屏蔽室通風設計理論基礎

屏蔽室通風設計主要是指對屏蔽室內部的通風量進行設計，其理論基礎為流體力學。本次屏蔽室熱設計使用CFD 軟件ANSYS Icepak 軟件對屏蔽室通風進行仿真設計。

1.1 CFD 仿真基礎

計算流體動力學（Computational Fluid Dynamics，CFD）主要通過計算機數值計算和圖像顯示的方法，求解流體力學和傳熱學等，在空間和時間上定量描述各物理量的數值解，從而達到對相關物理現象進行分析研究的目的[4-5]。其基本思想為：將時間和空間上連續的各物理量，如速度場、溫度場、壓力場等，用有限個離散單元上的變量值來替代，通過隱式方程建立有限個離散單元上變量之間的代數方程組，求解代數方程組，以獲得各物理場的近似值[6-7]。

ANSYS Icepak 使用隱式計算的方法，利用的連續性方程（Continuity Equation，也稱質量守恒方程）為：

動量守恒方程（Momentum Conseravation Equation，也稱Navier-Stokes）：

X 方向動量：

Y 方向動量：

Z 方向動量：

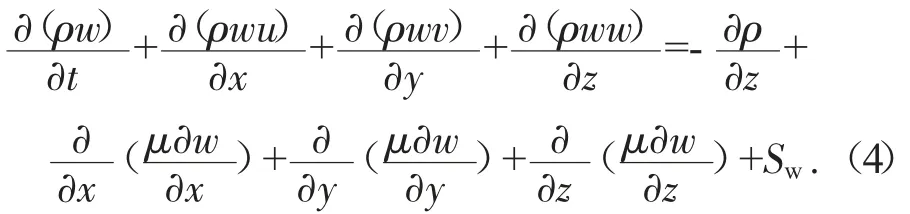
式中：u、v、w 為X、Y、Z 三個方向的速度；Su、Sv、Sw為動量守恒方程的廣義源項。

能量守恒方程為：

式中：Cp為比熱容；T 為溫度；ST為黏性耗散項。

1.2 自然對流模型選擇

ANSYS Icepak 提供兩類自然對流模型：一種模型為Boussinesq approximation，稱為布辛涅斯克近似；另一種模型為Ideal gas law，即理想氣體方程。

1）Boussinesq approximation：布辛涅斯克近似模型在自然對流控制方程中，動量方程浮力項中的密度是溫度的線性函數，而其他所有求解方程中的密度均假設為常數。浮力項中的密度公式為：

式中：ρ∞為周圍環境的空氣密度；t∞為周圍環境的空氣溫度；β 為周圍環境空氣的膨脹系數。

Boussinesq approximation 是ANSYS Icepak 默 認的自然對流模型，適用于大部分電子產品的自然散熱模擬計算。

2）Ideal gas law：當流體密度變化非常大時，使用Ideal gas law 理想氣體方程。由于屏蔽室內部通風流體密度變化較小，因此本次仿真使用Boussinesq approximation 對流模型。

2 屏蔽室通風設計方案

2.1 冷卻方式選擇

屏蔽室采用通風散熱的方式將內部設備進行冷卻，冷卻方法主要是根據期間的熱流密度和溫升要求進行選擇[8]，可參考圖2 進行。

圖2 冷卻方法的合理選擇

從圖2 中可以看出，本次研究的屏蔽室由于空間較大，且主要屏蔽材料均為金屬材料，因此，綜合考慮成本與維護便利性，采用強迫空氣冷卻的方法進行選擇。研究風扇布置方式，從而盡可能加大排風量，對促進屏蔽室熱設計有著現實意義。

2.2 風扇布置方式

本次研究五種風扇布置方式下屏蔽室通風量大小，目的是研究五種風扇布置方式時，改變出風口位置對通風量的影響。屏蔽室大小（長×寬×高）為6 500 mm×4 000 mm×3 000 mm，風扇采用EBMW6D800-GD01 風機，風機布置方式為4 個風機上下兩排呈2×2 陣列布置形式，該風機的流量揚程曲線如圖3所示。

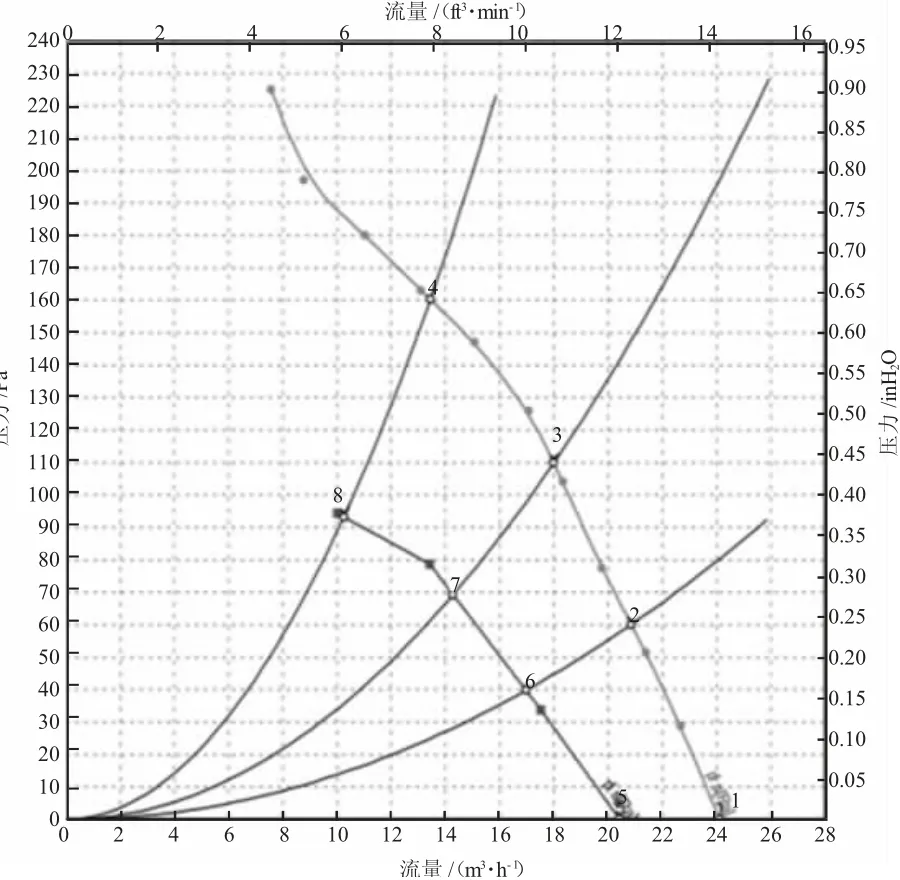
圖3 風機流量- 揚程曲線

出風口波導窗為Φ3.2 mm 波導，規格尺寸為800 mm×600 mm，開孔率為81%。波導窗由于有安裝法蘭，法蘭距離為50 mm，因此兩個通風波導的最近距離為100 mm。波導窗安裝孔距離為75 mm，因此，通風波導設計調整距離均為75 mm 的整數倍。據此分析以下五種通風設計方案，并對結果進行分析。

2.2.1 方案一

風機布置在側墻背面，與出風口相對布置，該方式布置風阻最小，具體布置方式如圖4 所示。將兩邊的波導窗依次從與中間的波導窗相距100 mm 沿橫向擴張到1 750 mm。

圖4 方案一

波導窗出風口風速與質量流密度如圖5 所示，依次向兩邊移動75 mm，處理各出風口仿真數據后，得到的出風口風量變化曲線如圖5 所示。

由圖5 可以看到，出風口出風量與距離的函數滿足二次方程，對該二次方程求導可得y'=1.2×10-6x- 0.001，可以據此分析出風量隨距離變化的變化率。在達到1 000 mm 后，出風量隨距離的增大基本不變，|y'|≤0.002。

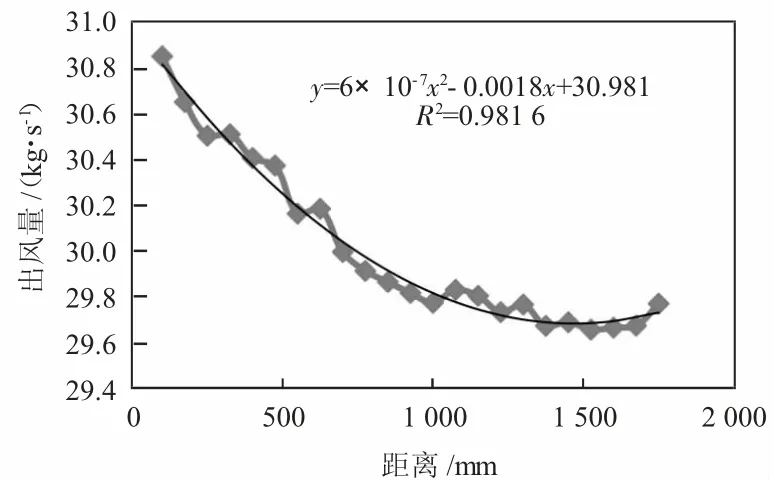
圖5 方案一出風量變化曲線

2.2.2 方案二

方案二進風口風機位置與方案一相同，出風口設置為將兩邊的波導窗依次從與中間的波導窗相距100 mm 沿縱向擴張到550 mm，如圖6 所示。

圖6 方案二

波導窗出風口風速與質量流密度如圖7 所示，依次向上下兩邊移動75 mm，分析仿真結果，出風周圍的波導窗風速逐漸減小，中間出風口速度逐漸增大，風速從垂直出門面逐漸變為有一定角度向上下兩邊擴散。統計各出風口出風量，得到的出風口總風量變化如圖7 所示。

圖7 方案二出風量曲線

由圖7 可以看到，出風口出風量與距離的函數滿足三次方程，對該三次方程求導可得y'=6×10-8x2-4×10-5x+0.004，可以據此分析出風量隨距離變化的變化率。在175～450 mm 之間變化率較大，其他位置出風量隨距離的增大基本不變，|y'|≤0.001 85。

2.2.3 方案三

風機布置在側墻背面，與出風口相對布置，該方式布置風阻最小，將兩邊的波導窗依次從與中間的波導窗相距100 mm 沿縱向與橫向分別擴張到550 mm，如圖8 所示。

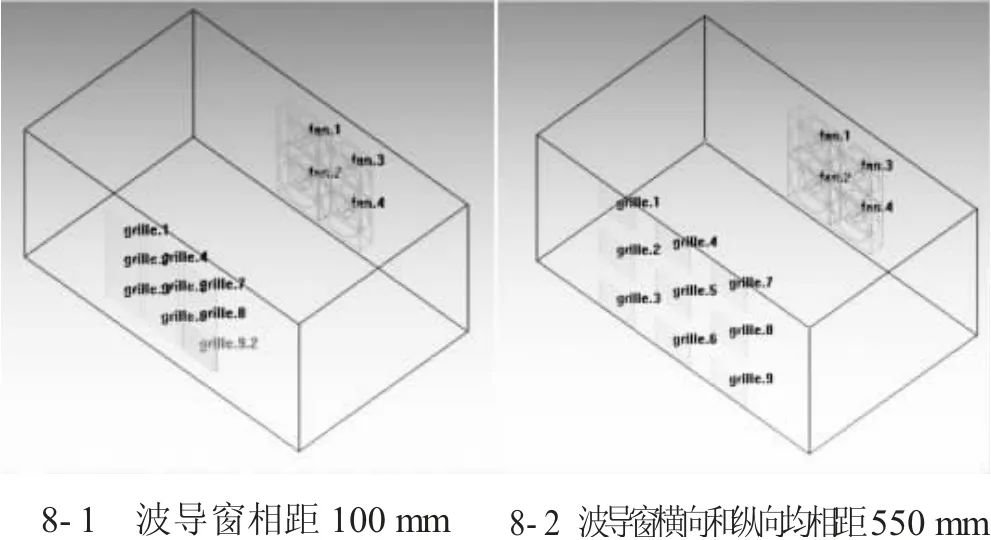
圖8 方案三

波導窗出風口風速與質量流密度如圖9 所示，依次向上、下、左、右四個方向分別移動75 mm，分析仿真結果，出風都集中在中間的通風波導窗上，向四周分散的波導窗明顯較方案一、方案二風阻大，向四周擴散的出風口較前兩種方案流量下降更快，前三種方案的風阻差別不大，都是適合在正對入風口和出風口的位置布置發熱設備的風道布置方式，但除了正對的位置，其他部位換氣量較小。對仿真數據進行處理，得到出風口總風量變化如圖9 所示。

圖9 方案三出風量曲線

由圖9 可以看到，出風口出風量與距離的函數滿足二次方程，對該二次方程求導可得y'=2×10-6x-0.002，可以據此分析出風量隨距離變化的變化率。在100～550 mm 之間變化率基本呈線性關系，出風量隨距離的增大而減小，|y'|≤0.000 9。

2.2.4 方案四

風機布置在頂部墻面的中后部，出風口布置在側墻上。將兩邊的波導窗依次從與中間的波導窗相距100 mm 沿橫向擴張到1 750 mm，如圖10 所示。

圖10 方案四

波導窗出風口風速與質量流密度如下頁圖11 所示，依次向左、右兩邊分別移動75 mm，方案四布置風速隨著波導窗距離的增加而不斷增大，出風角度相較之前的三種方案顯得更加復雜，向四周擴散開，出風量也沒有明顯規律，該布置方式風阻較大，適合在內部空間較大時使用，且出風口盡量分散布置。對仿真結果進行計算，得到出風口總風量變化如圖11 所示。

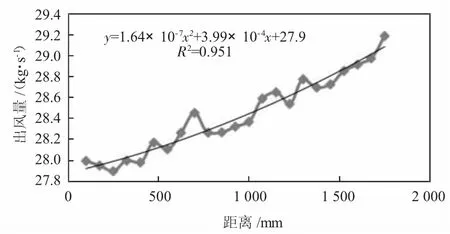
圖11 方案四出風量曲線

由圖11 可以看到，出風口出風量與距離的函數滿足二次方程，對該二次方程求導可得y'=3.28×10-7x+3.99×10-4，可以據此分析出風量隨距離變化的變化率。在100～1 750 mm 之間變化率基本呈線性關系，出風量隨距離的增大而增大，|y'|≤0.000 431 8。

2.2.5 方案五

風機布置在頂部墻面的側面，出風口布置在側墻上，進出風口呈90°布置。將兩邊的波導窗依次從與中間的波導窗相距100 mm 沿橫向擴張到1 750 mm，如圖12 所示。

圖12 方案五

方案五布置風速隨著波導窗距離的增加呈現振蕩波動，出風角度相較之前的三種方案顯得更加復雜，向四周擴散開，出風量也沒有明顯規律，該布置方式較方案一、方案二、方案三風阻較大，相較于方案四風阻略小，可以在側面設備需要散熱時使用，且可以根據設備位置布置出風口位置，而不會引起風阻的增加。對仿真結果進行計算，得到出風口總風量變化如圖13 所示。

由圖13 可以看到，出風口出風量與距離的關系不明顯，呈振蕩分布趨勢。將五種方案合并后觀察得到如圖14 曲線圖。

圖13 方案五出風量曲線

圖14 五種方案出風量曲線圖

深入分析可以發現，方案一和方案五的出風量隨著距離的增大不斷減小，具體數值差距如圖15 所示。

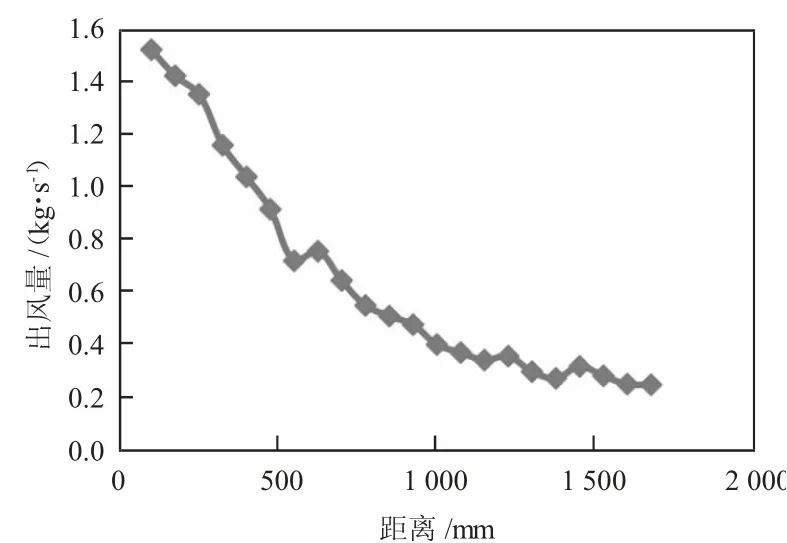
圖15 方案一與方案五出風量差值

由圖15 分析后可以看出，方案一和方案五布置方式出風量逐漸接近，最終穩定在0.21 kg/s 左右。

方案四呈上升趨勢，方案一呈下降趨勢，因此猜想方案一和方案四的風阻均值與方案五相同，因此，做如下分析，如圖16 所示。

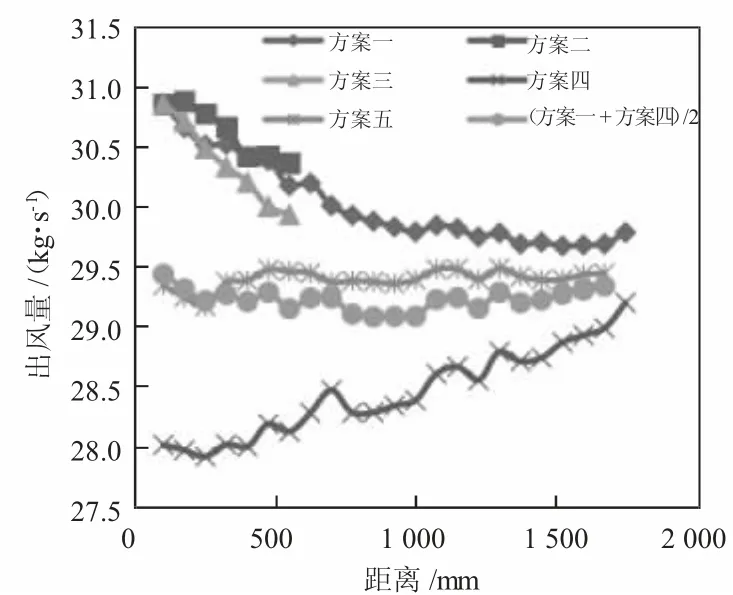
圖16 方案一與方案四均值與各方案趨勢圖

將方案一和方案四的均值與方案五分析可見，基本上與方案五的出風量是重合的。

3 結論

1）通過對五種方案進行對比得到如下規律：分析方案一、方案二、方案三可以發現，在進出風口相對布置時，出風量隨出風口距離增大而減小；分析方案四可以得出，出風量隨出風口距離增大而增大；分析方案五可得，在按照此種方式布置進出風口時，出風量與距離呈振蕩分布。

2）方案一、方案二、方案三的進風口布置方式風機受到的阻力最小；方案四進風口布置風機受到的阻力最大；方案五進風口布置風機方式風機受到的阻力介于方案一和方案四之間，且基本不會隨出風口布置距離的改變發生太大的變化。因此在設計通風時，可以將進風口與出風口按照規律合理設計，盡可能選用風阻最小的設計方法。