一種曲臂機構的優化設計

鄭繼平， 潘 彬， 宋 曦， 李春蓉， 周智輝

（湖南星邦智能裝備股份有限公司， 湖南 長沙 410600）

引言

高空作業平臺是用來運送操作人員和工作設備到指定高度進行作業的特種設備。隨著國家《無腳手架安裝作業技術裝備與產業化開發》重大項目的實施，極大提升了高空作業平臺的影響力[1]。曲臂式高空作業平臺以其靈活方便、可跨越一定障礙、在一處升降進行多點作業的特點而備受青睞[2]。曲臂機構由上連接體、下連接體、曲臂、連桿等組成。國內已有專業人士對曲臂高空作業平臺進行相關研究。張林生等對曲臂式高空作業平臺的結構進行過設計研究[3]；王思琪等對高空作業平臺變幅三鉸點進行優化[4]。這些研究僅限于整體結構和功能性的設計，鉸點計算也僅限于三鉸點研究，對于結構的具體細節設計和多鉸點的優化鮮有相關的文獻。本文對折臂機構中的上下連接體和折臂機構的上連接體和下連接體的平行四邊形機構及多鉸點機構進行優化設計，降低了油缸推力，保證了曲臂機構的舉升高度和穩定性能，實現了結構的優化設計。

1 一種曲臂機構

曲臂式機構如圖1 所示，其主要由臂架、主臂油缸、調平油缸、上連接體、上折臂、折臂油缸、下連桿、轉臺、下折臂、小連桿、下連接體、上連桿組成。主臂油缸驅動臂架的升降，改變臂架幅度，調平油缸用于上部工作裝置的調平，上連接體通過銷軸與臂架、主油缸、上調平油缸、上折臂、上連桿連接；下連接體通過銷軸與上折臂、上連桿、折臂油缸、下連桿、下折臂連接；轉臺是整個上裝的基礎，轉臺通過銷軸與下連桿和下折臂連接；下折臂通過小連桿與上折臂連接，折臂油缸與上折臂和下連接體連接，折臂油缸驅動折臂的展開和收攏。

圖1 一種曲臂式機構

2 折臂機構鉸點設計

2.1 折臂機構的幾何原理

折臂機構中各部件與軸的連接點在軸方向上投影的中心點稱為鉸點。連接體上鉸點的布置是否合理，不僅直接影響到折臂和主臂能否按照規定的作業曲線進行正常工作，而且直接關系到舉升油缸能否滿足工作要求，因此必須對鉸點的位置進行優化設計。上下連接體及折臂機構的鉸點如下頁圖2 所示。

圖2 曲臂式機構的鉸點

鉸點1~3 為主臂變幅鉸點，通過鉸點設計可以在滿足變幅角度的條件下使油缸力滿足工作要求。4~12鉸點為折臂機構的鉸點，通過鉸點設計可實現折臂機構的上下運動，實現折臂油缸力最小，并保證折臂機構實現臂架運動，滿足機構運動的各項指標要求。在折臂機構中，鉸點3、4、10、12 連線為平行四邊形，鉸點 12 的 坐 標 為，其中，L4-10為鉸點4 和鉸點10 的距離

鉸點5、原點、鉸點8、鉸點10 連線為平行四邊形， 鉸點8 的坐標為y8=L5-10sinarctan其中，L5-10為鉸點5 和鉸點10的距離

2.2 油缸力計算

根據力矩平衡關系，主臂油缸的油缸力大小F1=其中，M1為臂架及外載的力矩；L1為主油缸力的力臂；折臂油缸的油缸力為，其中，M2為臂架及折臂部分的力矩；L2為折臂缸的力臂。在機構運動工程中M1、L1、M2、L2是不斷變化的。計算出F1、F2在運動過程中的最大力，并通過鉸點優化使油缸力滿足設計要求。曲臂式機構缸力計算示意圖，如圖3所示。

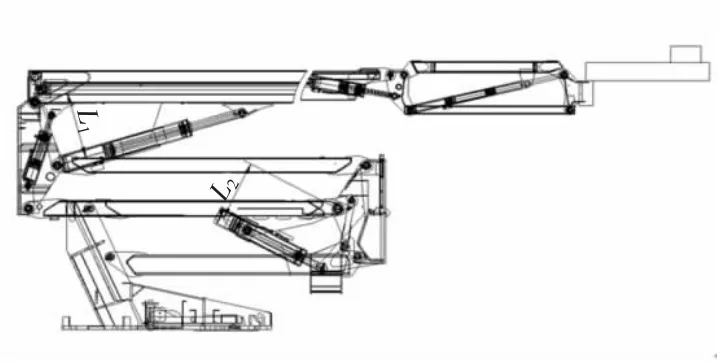
圖3 曲臂式機構油缸力計算示意圖

2.3 折臂系統動力學方程的建立

建立系統模型時，各零部件為剛體，折臂系統由14 個剛體組成，每個剛體有6 自由度，分別為x、y、z方向的平移和轉動自由度[5]。

采用拉格朗日乘子法建立系統運動方程[6]。

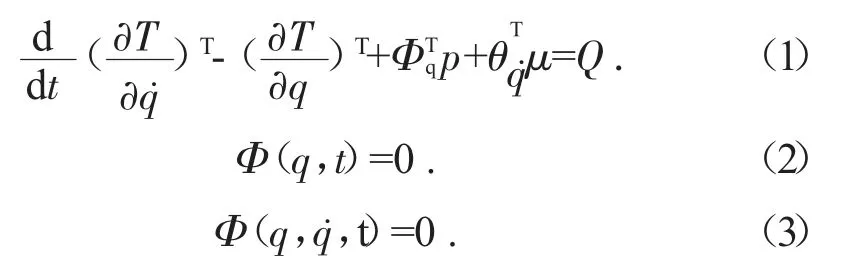
式中：T 為系統動能；Φ（q，t）=0為完整約束方程，Φ（q，q˙，t）=0為非完整約束方程，其中q 為廣義坐標列陣；Q為廣義力列陣；p 為對應于完整拉格朗日乘子的列陣；μ 為對應于非完整拉格朗日乘子的列陣。

2.4 采用遺傳算法進行鉸點優化

遺傳算法簡稱GA，是模擬生物在大自然中遺傳和進化過程形成的一種自適應全局優化概率搜索的方法。采用自然進化模型，按照優勝劣汰的原理，逐步迭代出越來越優化的解[7-8]。基本遺傳算法可定義為7個元組，表示為GA=（M，F，s，c，m，pc，pm），其中M 為群體大；F 為個體適應度評價函數；s 為選擇操作算子；c 為交叉操作算子；m 為變異操作算子；pc為交叉概率；pm為變異概率。

遺傳算法已成為各領域解決復雜問題的有力工具。遺傳算法流程如圖4 所示，在進行鉸點優化時，遺傳算法明顯優于其他算法[9]。折臂機構鉸點是由多個點構成的群體，在優化過程中需要通過適應值來判定是否滿足收斂條件，且應避免陷入局部最優點。鑒于此折臂結構的鉸點，采用遺傳算法進行優化設計。

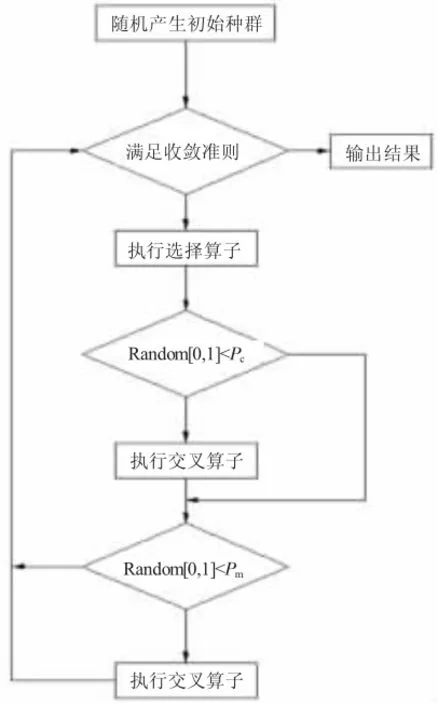
圖4 遺傳算法優化流程

2.5 LMS Motion 動力學模型的建立及優化計算

采用西門子公司的LMS Motion 對折臂機構建立模型，將銷軸連接處采用轉動副連接，油缸筒與油缸桿采用圓柱副連接，工作平臺及外載荷以質量塊替代，重力方向為Y 軸方向豎直向下。主臂油缸和折臂油缸通過圓柱副的軸向位移進行驅動，實現主臂的伸展及折臂的升降。建立模型如圖5 所示。將各鉸點進行參數化，參變量的設計如圖2 所示。

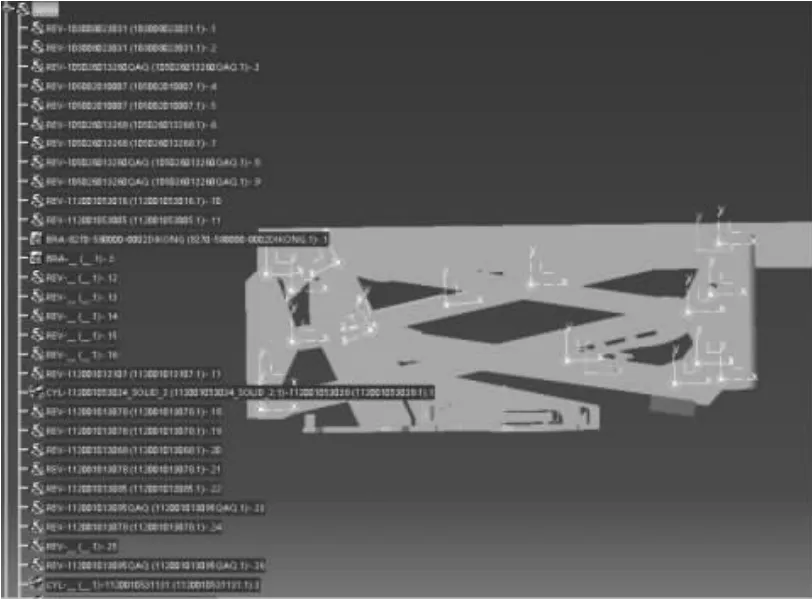
圖5 動力學模型

根據設計要求，主臂油缸力和折臂油缸力≤270 kN，平臺舉升高度22 m。采用遺傳算法對鉸點進行優化。

1）對主油缸鉸點1~3 進行優化設計。首先對設計變量相對主臂油缸力變化的靈敏度進行分析。結果如表1 所示。

表1 主臂油缸力靈敏度分析

由表1 可知y1、x2、y2、x3、y3的靈敏度稍大，因此優化y1、x2、y2、x3、y3變量。以油缸力最小化設計優化目標函數，將臂架仰角作為約束條件進行優化計算。優化結果如表2 所示。油缸力為247.75 kN，較優化前下降27.7%，油缸力滿足設計要求。鉸點優化前后主臂油缸力如圖6 所示。

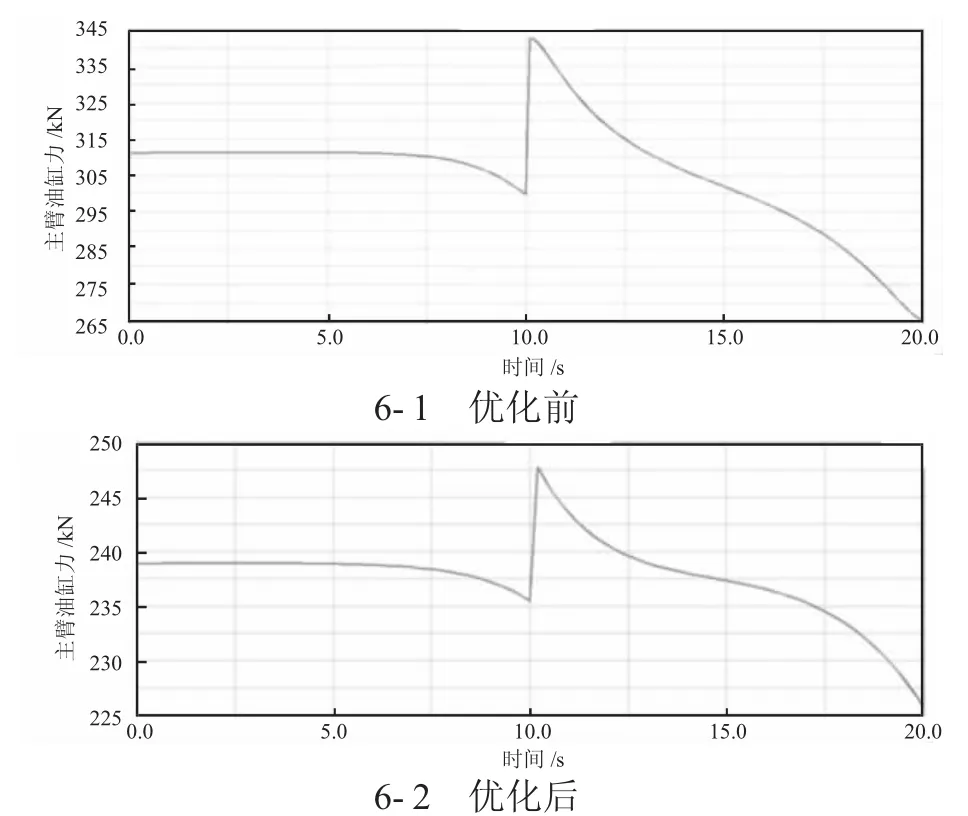
圖6 鉸點優化前后主臂油缸力對比

表2 主臂油缸力優化結果

2）對4~12 鉸點進行優化。為使折臂系統實現舉升要求，對折臂油缸力進行合理優化，各變量對于折臂油缸力的靈敏度如下：

綜合考慮折臂油缸力的影響因素，篩選優化變量為x5、y6、x7、y7、x9、y9、x10、y10、x11、y11，見表3 優化的目標為將折臂油缸力最小化設計優化目標函數，將上連接體與臂架的鉸點高度作為約束條件進行優化計算。

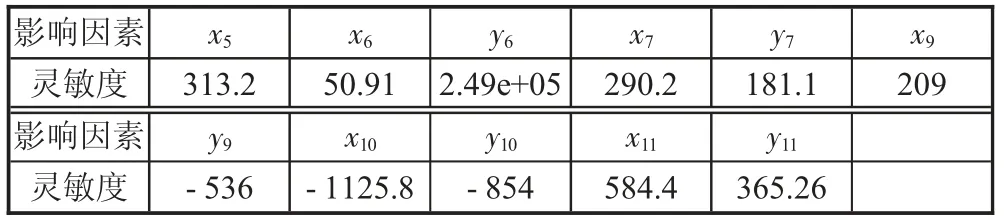
表3 折臂油缸力靈敏度分析

正確設計目標函數和約束函數，采用遺傳算法進行鉸點優化，見表4。優化結果如表5 所示。鉸點優化前后折臂油缸力如圖7 所示。由圖7 可知，最大油缸力為252.54 kN 較優化前下降23.56%，滿足設計要求。鉸點4 距原點的水平距離相差很小。折臂在起升過程中上連接體保持直線上升。曲臂平臺的穩定性滿足要求。舉升高度滿足要求，滿足設計要求。

圖7 鉸點優化前后折臂油缸力對比

表4 優化變量

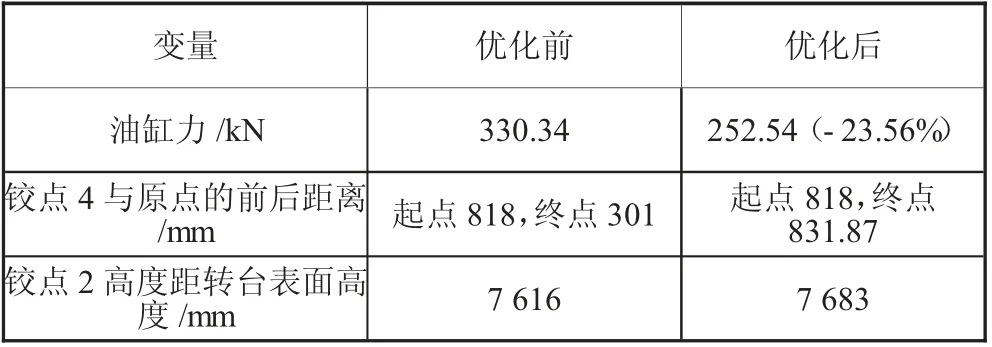
表5 優化結果

3 結論

1）經過對主臂及上連接體鉸點的優化設計，將主臂油缸力下降27.7%，有利于油缸的優化與匹配。

2）經過對上連接體和下連接體的鉸點的優化設計，將折臂油缸力下降23.56%，折臂油缸滿足設計要求。為油缸選型提供依據。且折臂舉升高度滿足設計要求，下連接體在上升過程中基本沒有前傾，臂架整體穩定性滿足要求。

3）優化設計方法能有效解決設計中的問題，實現設計中的最優解。軟件界面自動化操作方面有待進一步開展工作。