大數據分析技術在高校教育成本核算中的應用

賓揚帆

（湖南環境生物職業技術學院，湖南 衡陽 421005）

0 引言

自從我國全面建成小康社會以來，不僅在經濟建設上取得了巨大的成果，還將高校教育提上了改革計劃的日程。高校教育的目的就是培養出源源不斷的人才，為建設國家和服務社會提供人力資源。

目前我國高校教育中缺乏系統的資源管理，高校核算教育成本時通常采用較為粗糙的計算方法。這就導致核算值與實際應用值存在較大差別，使資源分配不均勻、資源浪費的情況時常發生。雖然在高校教育中投入了很多資源，但是效果卻不盡人意。高校教育成本核算方法成了研究的熱門話題。

隨著經濟的不斷發展，科學技術也在不斷創新發展。其中計算機科學的發展成果尤其顯著。計算機科學中的大數據分析技術被廣泛運用到生活中。大數據具有信息多樣性、能夠快速分析計算且數據庫規模較大的特點。大數據分析與信息融合技術的應用為人們的工作和生活帶來了很大的便利。

該文在此基礎上提出了大數據分析技術在高校教育成本核算中的應用。利用大數據技術優化高校教育成本核算方法，設計出更加科學合理的核算方法，以提高核算精確度，為高校管理者提供精準信息，為高校教育的管理提供依據。

1 基于大數據分析技術的高校教育成本核算設計

1.1 基于大數據技術的高校教育成本數據處理

在建模前要對所收集的高校教育成本數據文件信息進行預先處理，篩選出條件穩定的數據作為建模的基礎數據后再進行建模。具體的建模步驟如下。1）挑選數據試驗集合和練習集合。通常用于建模的數據分為2個不同的類型：第1種是對模型進行練習的數據集合，模型能夠在這個類型的數據集合中通過不斷學習優化出最適合的數據，并抓取數據中有用的信息進行標記，同時學習數據行為，將信息的輸入和輸出行為進行優化，構建相對穩定的行為習慣，再通過學習與帶有問題的數據進行對比，對整體數據庫的性能進行優化操作。第2種數據是試驗集合，當模型通過學習完成自我優化后，經過該數據集合能夠對模型的數據全面性進行優化。所以，采集數據時要關注這2種數據集合的樣本質量和個數。該文對模型進行設計時使用試錯的方法對第1種數據集合進行設置，利用對2種數據集合的設置使建模數據更加完整，強化了模型性能。2）對所采集的基本數據進行歸一化操作。對所采集的基本數據進行預處理在構建模型的前期準備中是十分重要的一步。由于基本數據是從不同的高校采集來的，所以數據的范圍和標準也不同，倘若直接將這些收集來的基本數據用于構建模型，會因為標準和數據范圍的不同而使模型在核算成本時不穩定，不能準確公平地進行成本核算。因此建模時要先進行預處理，將數據進行歸一化操作，統一數據的量綱和標準，減少數據之間的誤差。

在對所采集的高校教育成本基本數據進行歸一化處理時需要運用最大、最小化進行計算，如公式（1）所示。

式中：y為歸一化后的樣本數據值；y和y分別為歸一化后的樣本數據值的最大值和最小值；x為原始樣本數據值；和分別為原始樣本數據序列中的最小值和最大值。

1.2 成本核算數據核函數及核參數的確定

將高校教育成本數據進行線性化操作，一方面能夠大大增強模型的計算能力，當所要計算的高校成本教育數據信息過于龐大時，該操作能夠保證模型正常運行。另一方面，可避免計算時產生較大誤差，能夠有效提升模型的穩定性和準確性。該文運用核函數對高校教育成本數據進行處理，模型的核函數所在使用位置見表1。

表1 核函數設置表

核函數中的參數是核函數本身自帶的，核函數參數的取值規則是定義核函數最重要的標準。該文分別使用了2種不同的核函數進行模型的構建，能夠增強模型的穩定性和計算的準確性，避免模型在進行大數據計算時產生誤差。

1.3 構建高校教育成本核算模型

構建高校教育成本核算模型時需要運用靈活性較強的算法，這個算法需要效率高、計算精準，以保證模型的穩定性。選擇合適的算法來構建模型十分重要，該文采用人工蜂群算法來確定模型參數。人工蜂群算法在每次計算參數的過程中都會進行2次計算，一次是全面計算，一次是局部計算。2種計算方法相結合能夠更快更穩定地將模型參數計算出來，并能保證參數的誤差在合理的范圍內。該文所設計的模型需要在所收集的基本數據中挑選出相對較小的數據作為樣本構建模型。為了使構建模型時所用的參數更加合理、全面，需要對所收集來的數據信息進行全方位篩選。

該文所運用的人工蜂群算法中的偵察蜜蜂可通過不斷擴大偵查范圍、減小數據的極值誤差來提高算法的性能。在最開始的原始數據階段，新產生的資源會替代舊資源，以此來形成循環。這種方法雖然大大減少了數據計算的任務量，但是被替代的舊資源中還存在一部分對模型有用的數據，這就導致模型的基本數據不完善，形成參數時也不能保證參數的準確性，進而使模型在計算高校教育成本時出現誤差，削弱了模型的計算性能。

根據以上算法分析可知，使用人工蜂群算法時要對新產生的資源和被替代的資源都進行數據分析，以確保模型數據信息的完整性。所以該文引入Levy飛行算法與人工蜂群算法相結合的方法來計算數據信息。Levy飛行算法能夠在直線前進的計算路徑中找到一個直角的支線計算路徑，能夠保證數據信息在篩選、分析的過程中不落下任何信息點，確保模型基本樣本數據的全面性和完整性。同樣，2種算法相結合能夠很好地解決人工蜂群算法的局限性，將被替代的數據資源中的重要信息節點保存下來，并進行整合。一方面能保證數據信息都能夠被很好地利用，另一方面也加快了數據篩查、分析的速度，縮短分析的時間，提高了工作效率。2種算法相結合后的計算方法與之前單獨使用人工蜂群算法相比，不同的地方就在于偵察蜜蜂的步驟上，改變后的算法如公式（2）所示。

式中：u為任意路徑點的選擇；、、分別為路徑點的坐標號，其中為選定路徑點，和為隨機路徑點，∈{1，2，…，}，且≠，NS為資源的最大數量，∈{1，2，…，}，為人工設定的邊界；（）是一個隨機數，由Mantegna計算得到，如公式（3）所示。

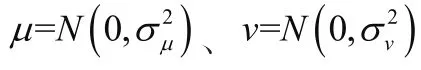
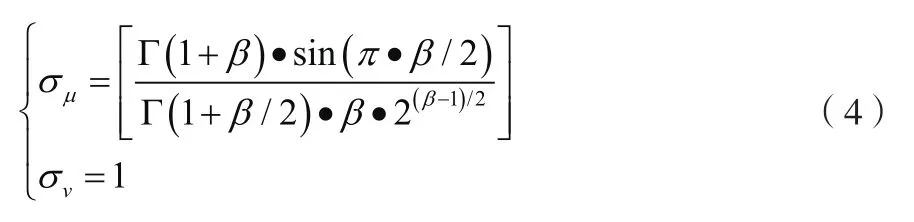
式中：σ和σ分別為函數分布的離散量，Γ() =(-1)!。

這2種算法相結合能夠較好地計算出模型構建時所用到的參數。利用參數能夠分析出高校教育成本的特點，然后根據不同高校所設置的規范對高校教育成本的影響因素進行具體分析，將這些影響因素整合處理，得到不同因素所占的比例，計算出這些因素的影響因子，輸入模型中，以保證模型在核算時能夠針對不同的高校進行個性化處理。

該文所設計的高校教育成本核算模型的具體構建流程如圖1所示。首先，將所采集的數據進行歸一化的預處理，形成模型基本數據。其次，將數據輸入模型中，使用試錯的方法對第1種練習數據集合進行設置，利用練習數據集合和試驗數據集合的設置使建模數據更加完整，強化模型性能。再次，確立核函數及核函數參數，進行模型的構建，增強模型的穩定性和計算的準確性，避免模型在進行大數據計算時產生誤差。最后，利用算法計算出合適的模型參數，將參數帶入模型中完成構建。最后根據指標評價對模型的性能進行評價。

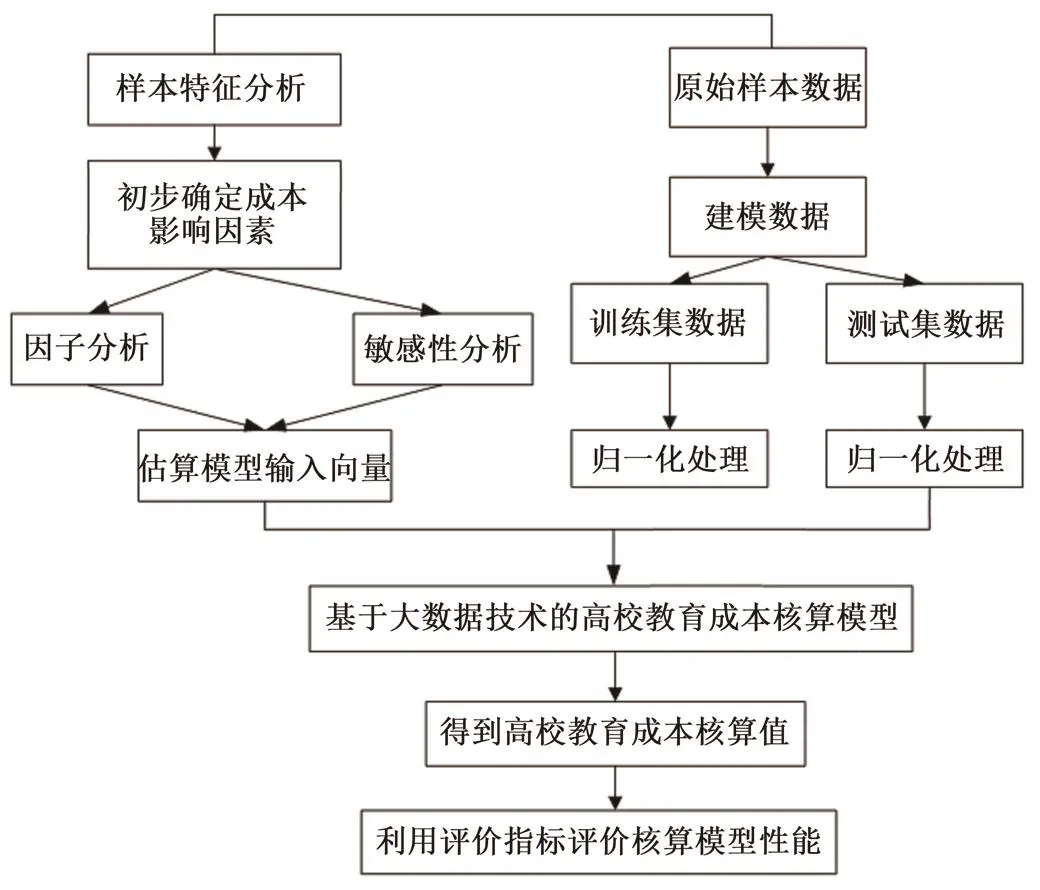
圖1 基于大數據技術的高校教育成本核算模型構建流程

2 試驗論證分析

為了驗證該文所設計的基于大數據技術的高校教育成本核算方法能否準確地將高校教育成本計算出來，該文選取了某高校作為試驗對象，收集該高校的教育成本作為建立模型的基礎數據。

首先，基于大數據技術對高校教育成本數據進行處理，為了保證高校教育成本的核算精確度，減小誤差，需要對高校教育的開支進行全面了解，將每項數據都記錄下來。教育成本中最難計算的就是高校固定資產的折舊。通過對該高校的資料收集可以看出該高校的固定資產包括教學樓、宿舍樓和辦公樓等各種建筑資產，計算機、電教設備、空調、實驗室儀器和體育教學用品等教學用具。根據這些固定資產的使用時間和未來價值進行評估計算，能夠得到固定資產的基本數據。再通過對這些固定資產進行評估和折舊處理，將其轉換為一定數量的金錢，作為數據輸入模型中，能夠減少核算誤差。

其次，對各初步確定的成本影響因素進行因子分析，以選擇的公因子的累計貢獻率超過80%為標準提取公因子。該文中不探討新的公因子的含義，只根據公因子系數的相對大、小判斷各初步確定的成本影響因素的重要程度，采用單因素敏感性分析方法，使各成本影響因素變動20%，計算出該影響因素的敏感性系數，判斷各影響因素對成本影響程度的相對大、小，同時計算各初步確定的成本影響因素的成本占比，將其作為篩選過程的輔助參考。根據資源的性質可以看出有一部分資源耗費與成本對象有可劃分的直接的關系，劃分標準就是資源動因，可以通過確定各個作業中心的資源動因數量對各個作業中心應分攤的成本數進行劃分。

某些類別的資源花費是專門屬于某一個作業的，這些類別的資源花費直接歸納到專屬的作業中心中，就能避免選擇相應的資源動因對其細分。

在高校的教、職工人員中，崗位劃分十分細致，不同崗位的教、職工人員的工資開銷也有所不同。所以要根據人數和工資，對不同崗位的教、職工人員進行單獨成本核算。不同崗位的教職工人員所占資源的分配見表2。

表2 分配率統計表

最后，提取其中的關鍵成本影響因子作為模型的輸入向量，采用經大數據技術調諧得到的正則化參數C和核函數參數σ的取值，并將不敏感系數ε=0.00作為模型的參數，完成高校教育成本核算模型設計。將測試集數據輸入高校教育成本核算模型得到各部分的成本核算值，比較成本實際核算值與該文的該文模型核算值，對比結果見表3。

根據表3可知，測試集中各樣本的成本估算值與實際值較為相近，而傳統方法核算出的數值與實際數值相差較大，說明利用該問所設計的基于大數據技術的高校教育成本核算模型具有較好的預測精度。該模型改善了傳統方法中高校教育成本核算值與實際值相差較大的問題。

表3 成本實際核算值與該文模型核算值的對比結果

3 結語

該文利用大數據技術設計出高校教育成本核算方法。通過大數據技術精確處理高校成本數據，確定成本核算數據核函數及核參數，構建高校教育成本核算模型。根據試驗結果可知，運用該文所設計的核算方法能夠大大降低核算誤差，提高核算的精確度，有助于高校的教育資源管理，為高校管理者提供了科學合理的成本核算方法。但由于時間限制，該文沒有對多個高校進行成本核算試驗，還需要在今后的研究中進一步完善。