碟形彈簧自復位梁柱鋼節點受力性能分析

朱麗華，韓 偉，寧秋君，劉海林

（1.西安建筑科技大學省部共建西部綠色建筑國家重點實驗室，陜西西安 710055；2.西安建筑科技大學土木工程學院，陜西西安 710055）

引言

自復位結構體系由復位元件和耗能元件組成，地震作用時由耗能元件耗散地震能量，地震之后通過復位元件實現結構的復位性能［1］。自復位結構具有殘余變形小，震后能快速恢復等優勢，因此受到國內外研究者的廣泛關注。1991 年，美國PRESS 計劃首次提出關于自復位結構的概念［2］。2001 年，RICLES 等［3］提出了由預應力鋼絞線復位的自復位鋼框架節點；2002 年，RICLES 等［4］對9 個大比例的后張拉自復位鋼框架節點進行了試驗研究；2008 年，GARLOCK 等［5］研究了不同設計參數對后張拉自復位鋼框架體系抗震性能的影響。ROJAS 等［6］和WOLSKI等［7］提出了由預應力鋼絞線復位的自復位鋼框架梁柱節點，并進行了試驗研究；2011 年，潘振華等［8］提出了由鋼絞線提供彈性恢復力的自復位鋼框架節點，并通過參數分析研究了該節點的抗震性能；2020 年，QIN 等［9］提出了由后張拉預應力鋼絞線提供彈性恢復力的自復位鋼框架節點，研究了鋼絞線預應力對該節點抗震性能的影響；HUANG 等［10－11］通過對后張拉自復位鋼框架節點進行低周往復加載試驗和有限元分析，研究了該節點的初始剛度，并提出了后張拉自復位鋼框架的設計方法；2021 年，HUANG 等［12］通過有限元分析研究了后張拉自復位鋼框架體系在不同地震作用下的抗震性能；FANG 等［13］、XU 等［14］和WANG 等［15］提出了碟形彈簧自復位阻尼器，并通過擬靜力試驗研究了碟形彈簧自復位阻尼器的抗震性能。

目前，自復位結構主要由預應力鋼絞線或預應力筋提供彈性恢復力，但預應力鋼絞線自復位節點的安裝方式相對困難；在荷載的長期作用下，會出現鋼絞線松弛和預應力下降等問題，進而影響結構復位能力。針對上述問題，本文提出了一種碟形彈簧自復位梁柱鋼節點，該節點的復位和耗能原理與普通鋼絞線自復位節點基本相同，其安裝方式比普通鋼絞線自復位節點簡單；此外，通過對碟形彈簧的合理設計能有效控制預應力下降的問題。

1 碟形彈簧自復位節點構造與受力分析

1.1 自復位節點構造

碟形彈簧自復位節點的基本構造如圖1（a）所示，該節點由碟簧裝置提供彈性恢復力，由腹板摩擦耗散地震能量。碟簧裝置由單耳板、外管、碟簧、拉桿和墊塊組成，碟簧參數包括外徑D、內徑d、自由高度H0、碟簧厚度t、壓平時變形量h0以及圓錐角θ，如圖1（b）所示。碟簧裝置具體構造如圖1（c）所示，單耳板與外管通過螺紋連接，碟簧兩端設置有墊塊，并以拉桿作為內導桿，以外管作為外導管，由碟簧提供彈性恢復力，其受力主要由拉桿傳遞。拉桿受拉時碟簧產生徑向變形，為保證碟簧變形不受阻，碟簧與外管和拉桿之間均設置有一定間隙。安裝自復位節點時，應先將摩擦板和雙耳板焊接在鋼柱加強板上，再將鋼梁和摩擦片安裝在摩擦板之間，并通過高強螺栓固定，最后安裝碟簧裝置；該節點主要以螺栓連接為主，具有較好的可安裝性。

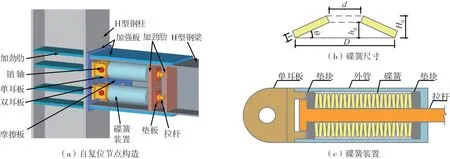
圖1 碟形彈簧自復位節點Fig.1 Configuration of self-centering connection with disc springs

1.2 自復位節點受力分析［16－18］

自復位節點的受力分析如圖2所示，開口之前，梁柱節點不發生相對轉動，此時，自復位節點可等效為傳統的剛性節點，其初始剛度k0可根據結構力學力法計算。

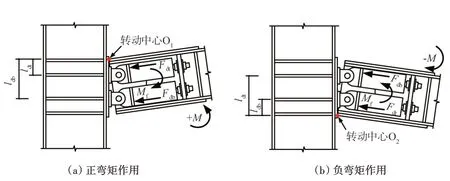
圖2 自復位節點受力分析Fig.2 Force decomposition of self-centering connection

自復位節點的開口彎矩主要由彈簧預壓力和腹板摩擦力提供，因此節點的開口彎矩為：

式中：F0為彈簧預壓力；ldt和ldb分別為上部碟簧裝置和下部碟簧裝置至轉動中心的距離；Mf為腹板摩擦力矩，可采用微元法計算，如圖3所示，其計算公式為：

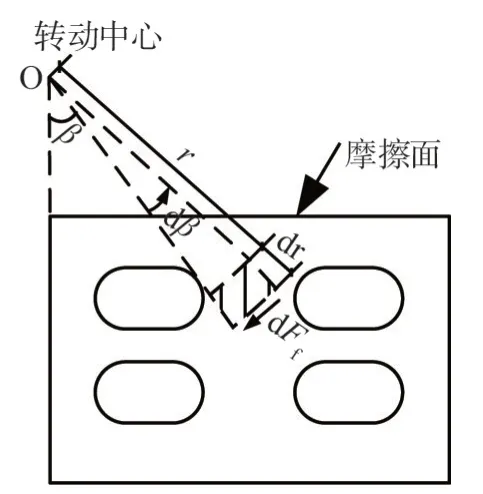
圖3 摩擦力矩計算簡圖Fig.3 Calculation diagram of friction moment

式中：μ為摩擦耗能裝置的摩擦系數；P為摩擦面單位面積壓力；Nb為單個高強螺栓預緊力；nb為高強螺栓個數；S為有效摩擦面面積。

自復位節點開口之后的剛度主要由碟簧裝置決定，因此節點開口之后的轉動剛度為：

式中：kd為碟簧裝置的剛度；n為碟簧疊合片數；fM為碟簧錐面間摩擦系數；α為碟簧壓板處的摩擦面數；fR為碟簧承載力邊緣處的摩擦系數；ks為復合碟簧的組合剛度。

自復位節點開口之后，摩擦力矩不再增加，節點的彎矩增量主要來自于碟簧裝置，因此節點的抗彎承載力為：

式中：θ為梁柱節點的相對轉角。

碟形彈簧自復位梁柱鋼節點的耗能性能是重要的性能指標之一，通常以等效阻尼比ξeq作為衡量指標，可根據式（7）計算：

式中，ED為自復位節點單周滯回耗能；ES為同等線彈性體系達到相同位移時所儲存的應變能。

2 有限元建模及分析

2.1 碟形彈簧建模及驗證

碟形彈簧是該自復位節點的關鍵部件，其力學性能對節點的受力性能影響很大，本文以文獻［17］中單片碟簧的試驗結果為依據，對碟簧的有限元模擬方法進行驗證，其中碟簧外徑為200 mm，內徑為102 mm，厚度為8 mm，自由高度為15 mm。采用ABAQUS 建立單片碟形彈簧有限元模型，并將有限元模擬結果與文獻［17］的試驗結果進行對比，如圖4 所示。由圖可知：數值計算結果與理論計算結果較為接近，與試驗結果有微小差異，整體而言，三種結果基本一致。由此可見：碟形彈簧有限元模擬的方法是可行的。

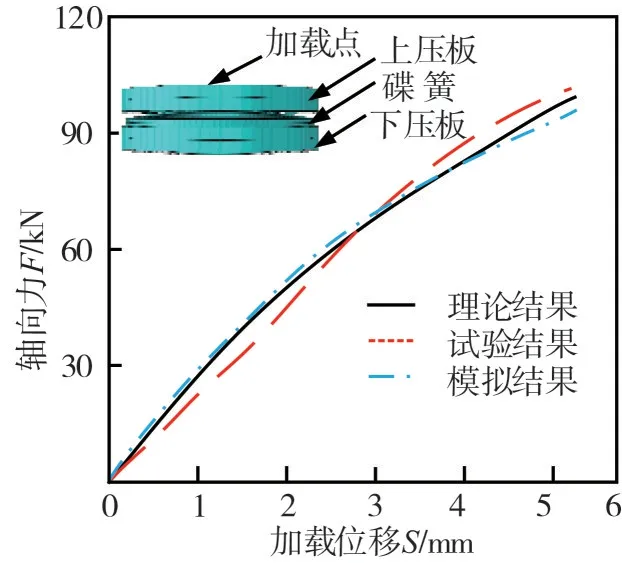
圖4 單片碟簧有限元模型及結果對比Fig.4 Finite element model ofsingle discspring and results comparison

2.2 碟形彈簧自復位節點建模

碟形彈簧自復位梁柱鋼節點的尺寸如圖5所示，鋼柱和鋼梁均設置有厚度為20 mm 的加勁肋和加強板。碟簧外徑為120 mm，內徑為37.2 mm，碟簧厚度為9 mm，碟簧減薄厚度為8.5 mm，自由高度為11.7 mm。碟簧裝置由24 片碟簧串聯而成，其剛度為5.67 kN/mm，除單耳板與外管之間建立綁定約束外，其余部件之間均建立摩擦接觸。鋼梁與碟簧裝置通過 36的10.9級高強螺栓連接，在鋼柱的翼緣上焊有厚度為14 mm 的摩擦板，在摩擦板與鋼梁腹板之間設置有2 mm 厚的黃銅摩擦片，摩擦片和鋼梁腹板均設置有長圓孔，其中摩擦板和摩擦片均設置在鋼梁腹板的兩側，并通過 22 的10.9 級高強螺栓與鋼梁固定。碟形彈簧采用屈服應力為1 400 MPa 的60Si2MnA 合金鋼，耳板和銷軸均采用屈服應力為980 MPa 的35 CrMo 合金鋼，其余構件均為Q345B。鋼材的彈性模量均為2.06×105MPa，泊松比均為0.3，其本構模型均采用雙線性隨動強化模型，其中強化模量為0.01E。

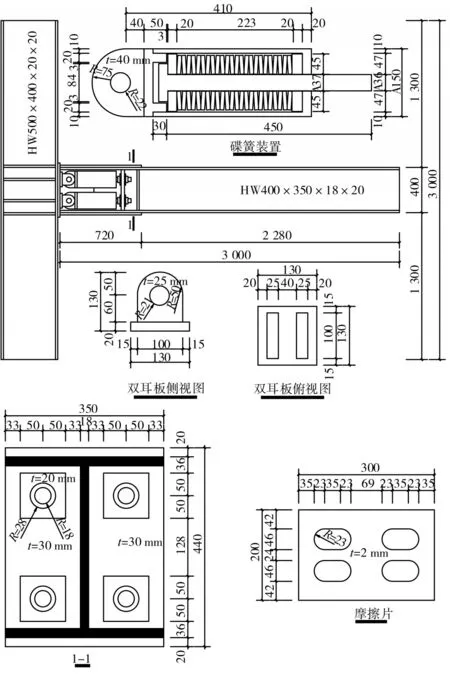
圖5 自復位節點構造及尺寸Fig.5 Dimension and detail of self-centering connection

柱頂和柱底均設置鉸約束，并在梁端分級施加低周往復荷載，第一級的位移值為5 mm；第二級的位移值為10 mm，以后各級的位移值按14 mm 增大，位移最大值為150 mm，對應的層間位移角為5%，每一級位移加載1 次，共計12 次。碟簧預壓力和螺栓預緊力分別為80 kN 和30 kN，二者均通過Bolt Load 施加。構件之間的相互作用根據工程實際建立，其中鋼構件之間的摩擦系數為0.2，碟簧錐面間的摩擦系數為0.03，碟簧承載力邊緣處的摩擦系數為0.03，黃銅摩擦片與鋼梁腹板之間建立綁定約束，摩擦片和摩擦板之間的摩擦系數為0.35。碟形彈簧自復位梁柱鋼節點有限元模型如圖6所示。

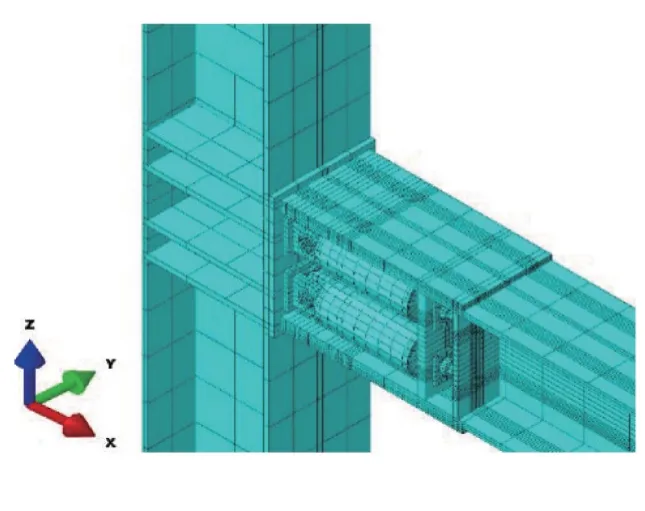
圖6 自復位節點有限元模型Fig.6 Finite element model of self-centering connection

2.3 分析結果

理論計算結果和有限元計算結果見表1，表中：θmax為最大層間位移角；Mmax為最大層間位移角所對應的彎矩。由表1 可知：有限元計算結果與理論計算結果的誤差較小，其中最大誤差僅為7.13%。由此可見：碟形彈簧自復位梁柱鋼節點的有限元建模方法準確可行。

表1 計算結果對比Table1 Calculation results comparison

碟形彈簧自復位節點的有限元計算結果如圖7所示，由圖可知：鋼梁的最大應力為334.5 MPa，碟簧的最大應力為1 113 MPa，自復位節點基本處在彈性階段；自復位節點的滯回曲線如圖8所示，該節點的彎矩－轉角曲線關于原點對稱，為典型的“雙旗幟形”。節點的開口彎矩為95.05 kN·m，當層間位移角為5%時，節點的抗彎承載力為149.74 kN·m。在開口之前，自復位節點幾乎不發生相對轉動，彎矩－轉角曲線基本保持線性，節點的初始剛度為9.79 kN/mm，具有較好的初始剛度；開口之后，自復位節點的剛度明顯下降，節點的彎矩－轉角曲線也基本保持線性；自復位節點卸載時的剛度與加載時的剛度基本一致，荷載卸載到零時，節點的相對轉角也接近于零。當層間位移角為2%時，節點的殘余變形低于0.2%，符合震后可修復的性能要求［19］。由此可見：碟形彈簧自復位節點具有較好的自復位能力。

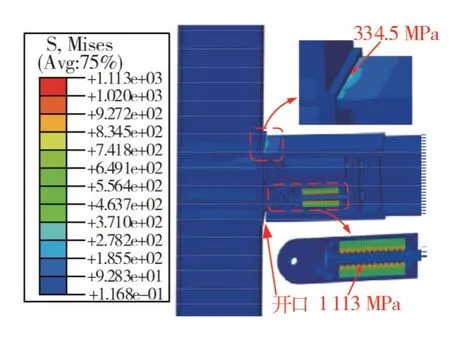
圖7 自復位節點有限元計算結果Fig.7 Finite element analysis results of self-centering connection

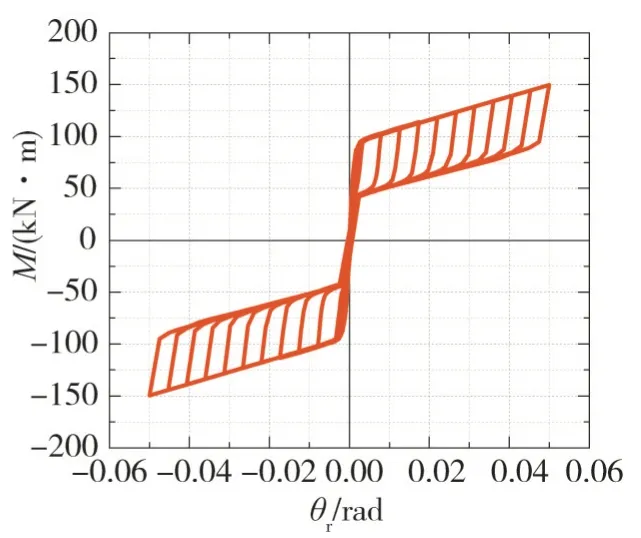
圖8 自復位節點滯回曲線Fig.8 Hysteric response of self-centering connection

3 參數分析

3.1 計算結果

碟形彈簧自復位梁柱鋼節點有限元分析結果見表2，表中：FB為腹板摩擦耗能裝置的螺栓預緊力；FS為碟簧裝置的彈簧預壓力；θres為自復位節點的殘余變形。

3.2 腹板摩擦耗能裝置的螺栓預緊力

為考察腹板摩擦耗能裝置的螺栓預緊力對自復位節點受力性能的影響，分析了螺栓預緊力分別為30 kN、45 kN和60 kN，其他參數不變的情況下自復位節點的受力性能。

由表2和圖9（a）可知：螺栓預緊力對自復位節點開口彎矩和抗彎承載力的影響較大，但對節點初始剛度和開口后剛度的影響較小。螺栓預緊力增大時，滯回曲線變得更飽滿，摩擦力矩也會隨之增大，從而增大節點的開口彎矩和抗彎承載力。

由表2 可知：螺栓預緊力從30 kN 增加到45 kN 時，等效阻尼比增加了33.3%，殘余變形增加了133%；螺栓預緊力從45 kN 增加到60 kN 時，等效阻尼比增加了18.9%，殘余變形增加了23.3%。由圖9（b）和圖9（c）可知：隨著螺栓預緊力的增大，自復位節點的耗能能力也會隨之增大，但自復位節點的復位能力卻隨之下降。雖然增大螺栓預緊力會使自復位節點的復位能力下降，但節點的殘余變形仍然較小，當螺栓預緊力為60 kN 時，節點的殘余變形僅為0.164%，自復位節點仍然具有較好的復位能力，因此增大螺栓預緊力能有效提高自復位節點的耗能能力。

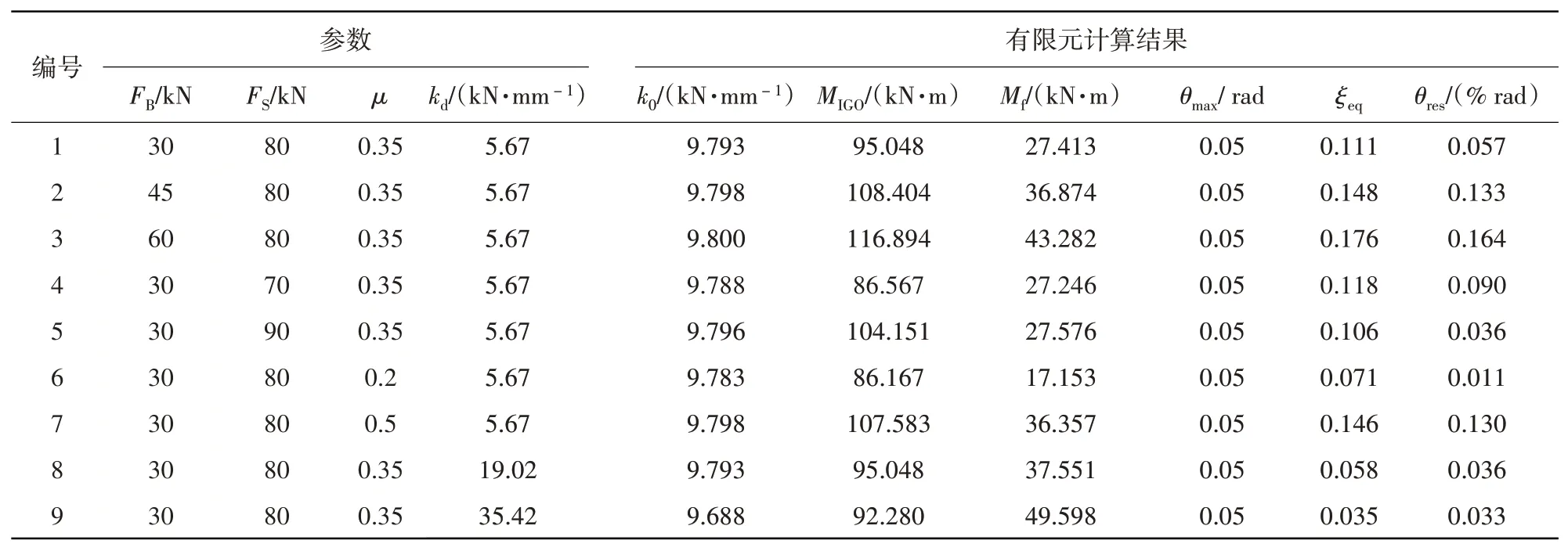
表2 有限元計算結果Table 2 Finite element method calculation results

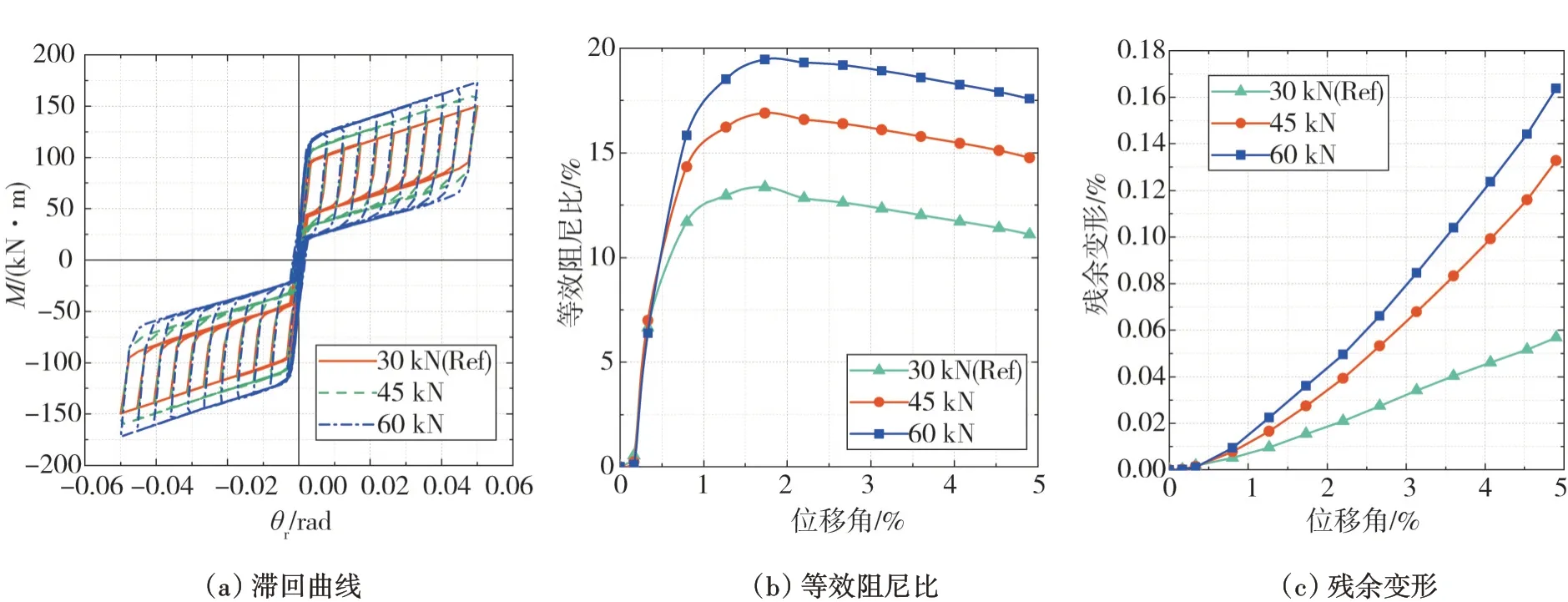
圖9 螺栓預緊力對自復位節點力學性能的影響Fig.9 Effects of the bolt preload on mechanical properties of self-centering connection

3.3 彈簧預壓力

考察了彈簧預壓力分別為70 kN、80 kN和90 kN，其他參數不變的情況下自復位節點的受力性能。由表2 和圖10（a）可知：彈簧預壓力對自復位節點開口彎矩和抗彎承載力的影響較大，但對節點初始剛度和開口后剛度的影響較小。彈簧預壓力增大時，彈簧力矩也會隨之增大，從而增大自復位節點的開口彎矩。自復位節點的初始剛度與剛性節點的剛度近似相等，自復位節點開口之后的剛度由碟簧裝置決定，因此彈簧預壓力對自復位節點初始剛度和開口后剛度的影響較小。

由表2 可知：彈簧預壓力為70 kN、80 kN 和90 kN 時，自復位節點的等效阻尼比分別為0.118、0.111 和0.106。彈簧預壓力從70 kN 增加到80 kN 時，自復位節點的殘余變形下降了36.7%；彈簧預壓力從80 kN 增加到90 kN 時，自復位節點的殘余變形下降了36.8%。由圖10（b）和圖10（c）可知：彈簧預壓力對自復位節點耗能能力的影響較小，但對節點復位能力的影響較大，并且隨著彈簧預壓力的增加，節點的復位能力也會隨之增大，因此增加彈簧預壓力能有效提高自復位節點的復位能力。

圖10 彈簧預壓力對自復位節點力學性能的影響Fig.10 Effect of spring preloads on mechanical properties of self-centering connection

3.4 摩擦系數

摩擦系數是影響自復位節點腹板摩擦耗能裝置的重要參數，為研究摩擦系數對自復位節點受力性能的影響，分別研究了摩擦系數為0.2、0.35和0.5，其他參數不變的情況下自復位節點的受力性能。

由表2 和圖11（a）可知：摩擦系數對自復位節點開口彎矩和抗彎承載力的影響較大，但對節點初始剛度和開口后剛度的影響較小。摩擦系數增大時，自復位節點的摩擦力矩也會隨之增大，從而增大節點的開口彎矩和抗彎承載力。

綜上所述，經產前彩超檢查能夠發現胎兒的肺內異常病灶，有利于對其病理性質和變化進行監測，因此常規的產前超聲檢查對于胎兒肺內病灶的發現以及評估和預后均有十分重要的價值。

由表2 可知：摩擦系數從0.2 增加到0.35 時，自復位節點的等效阻尼比增加了56.3%，殘余變形增加了418%；摩擦系數從0.35增加到0.5時，自復位節點的等效阻尼比增加了31.5%，殘余變形增加了128%。由圖11（b）和圖11（c）可知：增大摩擦系數能有效提高自復位節點的耗能能力，但節點的殘余變形也會隨之增大。雖然增大摩擦系數會增大自復位節點的殘余變形，但自復位節點的殘余變形仍然很小，當摩擦系數為0.5時，殘余變形僅為0.13%，自復位節點仍然具有較好的復位能力，因此增大摩擦系數能有效提高自復位節點的耗能能力。然而摩擦系數也不宜過大，否則會出現自復位節點無法復位和過早進入塑性的現象。

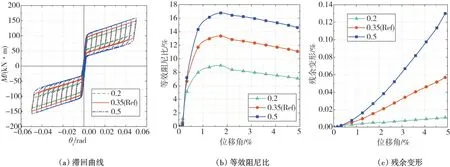
圖11 摩擦系數對自復位節點力學性能的影響Fig.11 Effects of friction coefficients on mechanical properties of self-centering connection

3.5 彈簧剛度

碟簧裝置的剛度主要取決于碟簧疊合數量和碟簧組合方式，本文分別考察了單片碟簧疊合、兩片碟簧疊合和三片碟簧疊合，其他參數不變的情況下自復位節點的受力性能，碟簧裝置的剛度分別為5.67 kN/mm、19.02 kN/mm和35.42 kN/mm。

由表2 和圖12（a）可知：彈簧剛度對自復位節點開口后剛度和抗彎承載力的影響較大，但對節點開口彎矩和初始剛度的影響較小。開口之后，節點的剛度主要取決于碟簧裝置，因此隨著碟簧裝置剛度的增加，節點開口之后的剛度也會隨之增大。在加載后期，自復位節點開口后剛度出現了增大的趨勢，以剛度為35.42 kN/mm 為例，當層間位移角為4%時，節點的開口后剛度開始出現增大的趨勢。這是由于當層間位移角為4%時，碟簧的變形量在0.75h0左右，此時碟簧的剛度會明顯增大，因此節點的開口后剛度會出現增大的趨勢。

由表2可知：彈簧剛度從5.67 kN/mm 增加到19.02 kN/mm 時，等效阻尼比下降了47.8%，殘余變形下降了36.8%；彈簧剛度從19.02 kN/mm 增加到35.42 kN/mm 時，等效阻尼比下降了40%，殘余變形下降了8.3%。由圖12（b）和圖12（c）可知：彈簧剛度對自復位節點耗能能力和復位能力的影響較大。當彈簧剛度增大時，自復位節點的復位能力也會隨之增大，但節點的耗能能力卻隨之下降。這意味著增大彈簧剛度能有效提高自復位節點的復位能力，但彈簧剛度也不宜過大，否則在加載后期會出現剛度不穩定的現象。

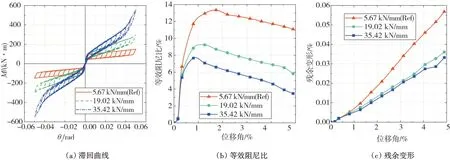
圖12 彈簧剛度對自復位節點力學性能的影響Fig.12 Effects of spring stiffness on mechanical properties of self-centering connection

4 碟形彈簧自復位節點恢復力模型

由有限元分析結果可知：碟形彈簧自復位節點的滯回曲線呈典型的“雙旗幟形”，符合自復位結構的基本特征。自復位節點的理論滯回曲線可分為4 個階段，每個階段所對應的剛度分別為k1、k2、k3和k4，如圖13 所示。在第一階段，梁端彎矩M小于節點的開口彎矩MIGO，梁柱之間不發生相對轉動，此時，自復位節點可等效為傳統的剛性節點，此時自復位節點的轉動剛度k1為：

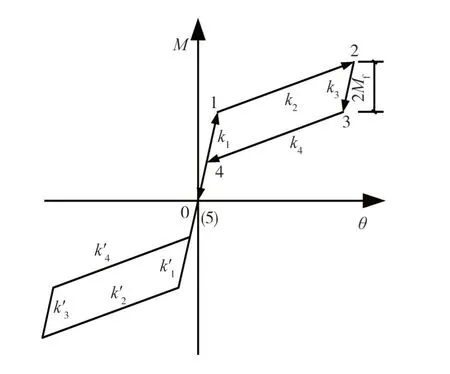
圖13 理論滯回曲線Fig.13 Theoretical hysteretic response

式中：l為梁端加載點至轉動中心的距離。

在第三階段，自復位節點的變形主要來自于鋼梁和鋼柱的彈性變形，梁柱之間幾乎不發生相對轉動，因此第三階段的剛度與第一階段的剛度近似相等，即：

卸載到3點時，摩擦力矩被克服，自復位節點開始發生反向轉動，因此3點的彎矩M3為：

在第四階段，摩擦力矩被克服，摩擦耗能裝置再次進入零剛度段，此階段的剛度主要由碟簧裝置決定，即：

卸載到4點時，自復位節點的開口閉合，碟簧裝置恢復到初始狀態，因此4點的彎矩M4為：

卸載到5點時，自復位節點恢復到初始狀態。

將上述恢復力模型的理論計算結果與有限元計算結果進行對比，如圖14 所示。由圖可知：恢復力模型的理論計算結果與有限元計算結果基本吻合。在第三階段，理論滯回曲線的剛度偏大，這是由于在推導恢復力模型時，假定其剛度與初始剛度近似相等所致。

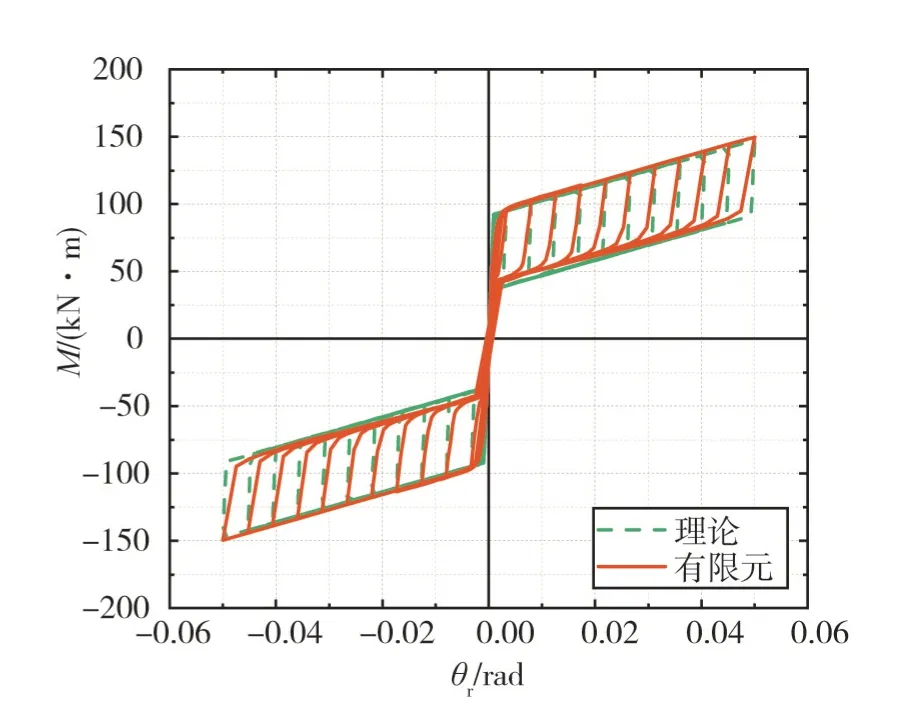
圖14 恢復力模型理論結果與有限元結果對比Fig.14 Comparison between theoretical results and finite element results

5 結論

本文提出了一種新型碟形彈簧自復位梁柱鋼節點，該節點的滯回曲線呈現典型的“雙旗幟形”，具有較好的耗能能力和復位能力。通過對該節點受力性能的理論分析和數值模擬分析得到如下結論：

（1）增大腹板摩擦耗能裝置的螺栓預緊力和摩擦系數能明顯提高自復位節點的抗彎承載力和耗能能力，但螺栓預緊力和摩擦系數也不宜過大，避免自復位節點過早進入塑性。

（2）增大彈簧預壓力能明顯提高自復位節點的抗彎承載力和復位能力；彈簧預壓力對節點的耗能能力沒有顯著影響。

（3）增大彈簧剛度能明顯提高自復位節點開口后剛度、抗彎承載力和復位能力，但彈簧剛度也不宜過大，以確保自復位節點具有穩定的開口后剛度。

（4）推導了碟形彈簧自復位梁柱鋼節點的恢復力模型，理論計算結果與有限元計算結果基本吻合。