不同林分密度指標在杉木單木直徑年生長模型的應用

姜 麗，張雄清，段愛國，張建國

（中國林業科學研究院林業研究所，國家林業和草原局林木培育重點實驗室，北京 100091）

林分密度指標是評定一個時期林分生長密度的尺度指標，而確定合適的指標是開展林分密度研究的重要前提。Dean[1]認為林分密度指標則至少需要滿足以下3個條件：（1）與林分生長有關；（2）與立地質量、林分年齡等無內在聯系；（3）較為容易測量得到。林分密度指標有多種，如：Reineke林分密度指數（SDI）[2]，Nilson密度指數 （SD）[3-4]，優勢高-營養面積比[5]，相對密度RD指數[6]，以及相對植距RS指數[7]等。這些密度指標的提出均是處于一定的條件下，每個指標都有其使用條件及適用范圍。選用不同的林分密度指標會直接影響著所建模型的精度與預估結果，因此選取合適的密度指標建立單木生長模型顯得尤為重要。

基于林木長期生長數據，預估單木年生長量時，之前常用的固定生長率法是假設在森林的整個生長期內，林木的生長率是固定不變的這一假設進行的研究。顯而易見，這種假設并不符合現實規律，隨著林分生長時間的推移，所用于預估模型中的特征因子（林分優勢高、林齡、林分密度）和林分中單木的特征因素（樹高、胸徑）等在每一個生長階段都會有變化，必然也會導致單木生長量的變化。為克服固定生長率法的這個缺陷，不少方法被陸續提出，如內插法和迭代法等。Cao等[8]基于迭代法提出的可變生長率法。該方法將林分生長期間林分與單木因子變化引起的單木年生長量變化納入分析，并且用時比迭代法更少。張雄清等[9]比較了可變生長率法與固定生長率法，發現可變生長率法表現更好。

杉木（Cunninghamia lanceolata （Lamb.）Hook.）是中國南部地區最重要的用材林樹種。本研究基于可變生長率法構建包含不同林分密度指標的杉木單木直徑年生長模型，選出適宜單木直徑年生長模型的最優林分密度指標，以期實現杉木人工林單木直徑生長的精準預測，為實現杉木人工林質量精準提升提供密度管理支撐依據。

1 研究數據與方法

1.1 研究區域及數據

樣地設置在福建武夷山北部的邵武市，位于117°43′ E，27°05′ N。地貌特征主要是高山和低丘陵地區，海拔為250～700 m，坡度為25°～35°，為亞熱帶季風氣候，年平均溫度17.7 ℃，1月平均溫度6.8 ℃，7月平均溫度28 ℃，最低極端氣溫為?7.9 ℃，年日照時間1 740.7 h，平均霜凍期為95 d。年降水量1 768 mm，年平均相對濕度為82%。林下植被有中華杜英（Elaeocarpus chinensis （Gardn.et Champ.） Hook.F.ex Benth.）、胡頹子（Elaeagnus pungens Thunb.）、狗脊（Woodwardia japonica （L.f.） Sm.）、芒萁（Dicranopteris pedata （Houtt.） Nakaike）、烏毛蕨（Blechnum orientale L.）和扇葉鐵線蕨（Adiantum flabellulatum L.）等。

試驗林使用1年生苗木于1982年造林，完全隨機區組設計，分5種造林密度：A：2 m×3 m（1 667 株·hm?2），B：2 m×1.5 m（3 333株·hm?2），C：2 m×1 m（5 000 株·hm?2），D：1 m×1.5 m（6 667 株·hm?2）和E：1 m×1 m（10 000 株·hm?2）。每個樣地大小為 20 m×30 m，每種造林密度均重復3次，總計15個樣地。標記了一共4 800棵樹，在冬季測量樹高和胸徑，從1984年至1990年，每年進行1次測量；從1992年至2010年，每隔1或者2年進行1次測量。具體統計數據見表1。研究數據隨機抽取60%用于模型構建，剩余40%用于模型驗證。

表1 杉木人工林林分和單木變量統計Table 1 Summary statistics of stand and tree variables of Chinese fir plantation

1.2 研究方法

利用常用的7種林分密度指標，分別是每公頃株數密度N、每公頃胸高斷面積Ba、林分密度SDI指數、SD指數、優勢高—營養面積比Z指數、相對密度RD指數和相對植距RS指數構建杉木單木直徑生長模型。

1.2.1 林分密度指標

（1） SDI指數

SDI指數[2]是通過單位面積上林木的株數與林木的平均胸徑的關系確定的，是反映林分直徑分布與林分內單位面積的株數之間關系的綜合指標。因此，SDI密度指數在林木密度管理中使用較常見，其數學表達式為：

式中：Dq為林分平方平均胸徑cm；D0—林分標準直徑，杉木一般取值20 cm；β為Reinek自稀疏系數，一般取值?1.605。

（2） SD指數

根據Nilson[3-4]對林木之間的平均距離L和胸徑Dq的定義，林分相對密度SD指數的公式如下[10]：

式中：a，b為參數，k=?a，D0—取20 cm。

（3）優勢高—營養面積比Z指數

劉金福等[5]采用單位面積內株數與優勢木的平均高來反映林分中林木的相對密度的大小。其表達式如下：

式中：N—每公頃株數；Hd—優勢木平均高。

（4） 相對密度RD指數

Curtis[6]提出利用林分斷面積和平方平均胸徑計算林分密度指標，該指標簡單，容易計算[11]，其公式如下：

（5）相對植距RS指數

相對植距是跟立地、胸徑等因子無關的林分密度指標，表達式如下[7]：

1.2.2 單木直徑年生長模型 構建單木直徑生長模型，可以引入多個自變量，其中包括單木特征因子（樹高、胸徑等）和林分特征因子（林分密度、林齡、林分優勢高等）。一般這些因子歸為3類：林齡、競爭因子和立地因子。而立地因子中，一般以林分優勢高表示。因此，在單木的生長過程中，主要是受到競爭、立地和林齡的影響。在本研究中，選取了林齡（A）、7種林分密度指標和林分優勢高（Hd）構建杉木單木直徑生長模型。基于可變生長率法，利用遞歸的方式推導過程如下[9]：

（t+1）年時:

（t+2）年時:

（t+q）年時:

式子中：Di,t為t年時第 i株林木的直徑（cm）；

At為t年時林分的平均年齡；

K為7種林分密度指標：包括林分胸高斷面積（BA）、優勢高營養面積比（Z指數）、株數（N）、相對植距（RS）、林分密度指數（SDI）、相對直徑（RD）和SD指數；

Hdt為t年時的林分優勢高；

α1～α4為模型參數；

將林分變量因子，如林分優勢高等每年的變化納入分析，通過建立模型預估對應的林分變量，再將預估出來的林分優勢高用來建立杉木單木直徑生長模型。林分優勢高模型形勢如下：

其中β1、β2為待估參數。

本研究中，杉木單木直徑模型的參數估計均利用SAS中非線性回歸模塊來完成。利用可變生長率法估計模型參數時，應用了循環運算，直到循環停止。

1.2.3 模型選擇評價 林分優勢高模型和單木直徑生長模型通過統計量平均絕對偏差（MAD）、均方根誤差（RMSE）和決定系數（R2） 進行評價。

2 結果與分析

杉木林分優勢高模型的參數估計結果及模型的均方根誤差、決定系數見表2。從模型結果中參數的標準誤差可以得知，模型的參數估計值均為有效值，并且模型的決定系數很高，達到了0.953 9，均方根誤差RMSE較小，為1.343 1。因此林分優勢高模型可用來預估杉木林分優勢高。

表2 杉木林分優勢高模型的參數估計、標準誤差、決定系數及均方根誤差Table 2 Parameter estimation,standard error,R2 and RMSE of dominant height model of Chinese fir.

本研究分別用7種不同林分密度指標，利用可變生長率法建立了7種杉木單木直徑生長模型，得到的參數估計和標準誤差及模型評價見表3。由表3可知，大多數模型參數估計值的標準誤差都在接受范圍之內，因此模型參數估計值都是有效的。從決定系數R2可以得到模型的擬合效果都相當高，均在0.965以上。7類將密度指標納入分析的杉木單木直徑模型精確度，大部分都高于不含密度指標模型。只有以相對直徑RD為密度指標的模型，其決定系數、均方根誤差和平均絕對偏差與不含密度指標的模型一致。其次，從模型參數估計α3也可以發現，其標準誤比較高，參數估計在0.05水平不顯著，相對直徑參數估計不穩定。因此可以得到在杉木直徑模型中，相對直徑RD并不適合作為模型的密度指標。

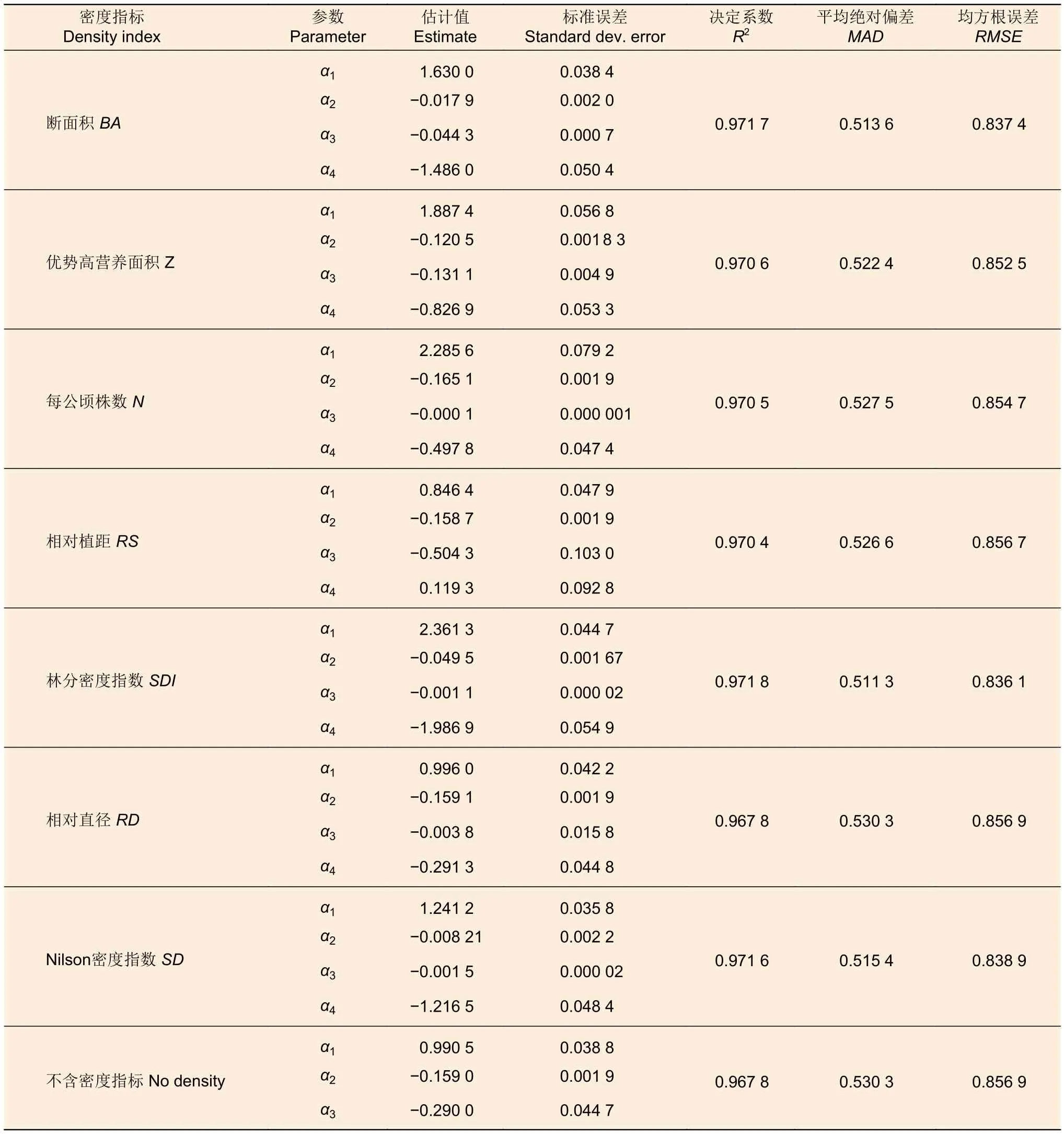
表3 不同林分密度指標應用于杉木單木直徑生長模型的參數估計及模型評價Table 3 Parameter estimation and model evaluation of annual tree diameter growth model of Chinese fir with different density indices

所有含有密度指標的模型中，模型決定系數最高的為以林分密度指數（SDI）為密度指標的模型，為0.971 8，同時也有最低的平均絕對偏差以及均方根誤差，分別為0.511 3、0.836 1。模型精度其次為以林分斷面積BA和Nilson密度指數為密度指標的模型，R2分別為0.971 7、0.971 6。其余5種林分密度指標表現介于表現最佳SDI指標（0.971 8）和最差RD指標（0.967 8）之間，所得到的模型精度從大到小依次為林分斷面積BA（0.971 7）、Nilson指數SD（0.971 6）、優勢高營養面積比Z（0.970 6）、每公頃株數N（0.970 5）和相對植距RS（0.970 4）。

基于最優的含SDI指數建立的單木直徑生長模型，繪制了模型殘差圖。從圖1中可以看到，模型在直徑較小的時候，如0＜D≤5 cm，傾向于低估杉木單木直徑生長；在5＜D≤20 cm的時候，模型傾向于高估單木直徑生長；在D＞20 cm的時候，模型則更傾向于低估杉木單木直徑生長。總的來說殘差均勻分布在0附近，服從正態分布，總體模型情況較好。

圖1 包含SDI指數的單木直徑生長模型的殘差分布Fig.1 Residual distributions of annual tree diameter growth model including SDI

從所有模型的參數估計方面來看，α2在所有模型中均為負值，且α2與林齡A相關，可以看出杉木單木直徑增長與年齡在任何密度指數下均呈現負相關關系，即隨著林分年齡的增大，單木直徑生長量減小。α3在所有模型中均為負值，且是林分密度指標因子的系數，可以得到杉木單木直徑生長隨著密度指標的增大而減小。α4在所有模型中得到立地估計均為負值，且與林分優勢高Hd的倒數負相關，因此隨著林分優勢高的增大，杉木單木直徑生長量增大。林分優勢高通常可以代表立地質量，即林分優勢高越大立地質量越好，杉木直徑生長量也就越大。

3 討論

一般情況在預估單木的年生長量時，主要是基于樹干解析中年輪寬度分析[11]。但是利用樹干解析分析單木年生長量時需要伐倒樹木，而且所選擇的解析木一般是選擇平均木，并不能完全代表整個林分的生長狀況，其次樹干解析需要耗費大量的人力物力[12]。近年來，基于已有的連續調查數據，學者研究和利用單木生長模型來預估單木年生長量。例如，為了獲得單木年生長量（如胸徑、樹高和材積），通常用的方法是固定生長率法，其前提是假設在整個生長期，各單木的年生長量是保持不變的。一般常用定期平均生長量來代替年生長量[7]。很明顯該估計方法比較簡單，并不符合林木的實際生長規律。因為隨著森林的演替過程，一些林分的特征（立地，年齡，林分競爭等）和單木本身的一些因子（胸徑，樹高，冠幅等）都會隨著林齡變化而變化，因此也必然會導致單木每年的生長量也發生變化。為解決固定生長率法的缺點，Mcdill和Amateis[13]提出利用內插法來估計單木年生長。之后Cao等[8]也基于內插法模擬單木直徑、樹高和樹冠比的變化，發現內插法比固定生長率法的模擬效果要好的多。然而，內插法的前提是在單木年存活率不變。為進一步提高模型的預測精度，Cao[14]提出了迭代法。該方法比固定生長率法和內插法均表現出明顯的優越性，因為該方法考慮了單木在生長期間，林分因子（如競爭和林分優勢高）及單木本身的變化而引起的單木直徑年生長量的變化。Cao[15]基于迭代法提出了可變生長率法，該方法也是考慮了林木在生長期間，林分變量如競爭和林分優勢高及單木本身的變化而引起的單木胸徑年生長量的變化。而且可變生長率法在估計模型參數時，比迭代法簡單，計算耗時較少[16]。張雄清等[9]利用可變生長率法構建了油松單木直徑和存活率的預估模型，模型擬合效果很好。之后張雄清等[12]基于可變生長率法構建了單木油松年生生長模型，發現該方法不僅能夠很好地預測單木斷面積生長，而且很好地解決了調查間隔期不一致而導致的相容性情況。

本研究發現密度指標的估計值為負數，說明單木直徑生長隨著密度的增加而減少。杉木單木的生長主要依靠良好的光照，充沛的水資源以及土壤營養物等，在林分密度增大的情況下，必然會導致樹木間對光照、水資源、營養物質等的競爭，競爭的后果則會導致單木直徑生長量的減少。即隨著競爭強度的增大，樹木的生長量會減少，這與之前學者們的結論是一致的[17]。此外表明，用林分密度指數SDI建模預測杉木單木直徑生長的模型是最佳選擇，這與高啟東等[18]研究結果一致。許多學者認為SDI指數的主要優點就是它整合了林分的株樹密度和平均直徑[19-20]。Zeide[21]報道稱在純林中，SDI指數是最簡單而且描述林分密度最有效的一個指標。正是由于SDI指數的優點，多數學者把SDI指數引入生長模型中來表示林分密競爭指標[22-24]。也有學者在生長模型[25]和過程模型[26]中引入了SDI指數并得到了很好的擬合結果。此外，也有學者認為Nilson密度指數（SD）是最優林分密度指標，如車少輝等[27]認為林分密度指數SDI可以與相對植距RS相互轉換。模型表現最差的為相對直徑RD模型和不含密度指標模型。因此，在構建杉木單木直徑生長模型，將相對直徑RD以外的林分密度指標納入模型是非常必要的，可顯著提高模型估計的精確度。

4 結論

本研究基于可變生長率法，應用7種不同的林分密度指標以及不含有密度指標，構建得到了8種杉木單木直徑年生長模型，模型的擬合精度比較高，R2均在0.96以上。相比較含有密度指標的杉木單木直徑模型精度，高于不含密度指標模型。在所有含有密度指標的模型中，決定系數最高的是以林分密度指數（SDI）為密度指標的模型，其次為以林分斷面積BA和Nilson密度指數為密度指標的模型。因此，在估計杉木直徑年生長量模型時，應該考慮引入Reinek提出的 SDI密度指數，以實現杉木人工林生長的精準預測。