不同強度準則對預測巖石抗拉強度的適用性

楊宇

（1.山西省交通科技研發有限公司，山西 太原 030032；2.山西省智慧交通研究院有限公司，山西 太原 030032）

0 引言

巖石強度理論可以表征巖石在破壞條件下的應力狀態和強度參數之間的關系，是巖土工程設計的理論基礎[1]。目前，大部分強度準則是基于巖石三軸壓縮試驗提出，即考慮巖石的3個主應力，主要反映巖石的抗壓和抗剪性能。但是，在一些工況下，需要巖石承受拉張應力，而且巖石抵抗拉應力的能力很差。例如，在地質構造穩定的山區進行硐室開挖，硐室上覆圍巖層理水平，在硐室開挖后，頂端圍巖在自重應力的作用下，會產生向兩側的拉應力，使得上覆巖層發生拉張斷裂，對硐室穩定性造成影響。因此，在工程中，巖石抗拉強度是一個重要的力學參數。

目前，測試巖石抗拉強度的方法有很多，在現場主要通過點荷載試驗測定抗拉強度，但是這種方法測得的結果離散型較大，只能粗略反映抗拉強度，若要得到更準確的抗拉強度，還需要借助室內力學試驗進行測試。主要的室內測試方法有兩種，直接拉伸試驗和間接拉伸試驗，直接拉伸試驗可以精確地測得巖石抗拉強度，但是由于其試樣制備困難，沒有得到較廣泛的使用。間接拉伸試驗包括劈裂法和抗彎法，其中劈裂法應用最為廣泛。但是劈裂法也存在很多問題，譬如加載方式、試樣尺寸、計算方法等，國內外學者進行了相關的研究，這里不作贅述。

雖然關于巖石抗拉強度的研究逐漸深入，但是還存在諸多問題，巖石破裂形態與抗拉強度的關系尚不明確，間接拉伸法計算巖石抗拉強度中的誤差分析，考慮巖石各向異性的抗拉強度計算等。基于此，本文結合前人研究成果，對比不同破裂形態，對傳統抗拉強度計算公式進行了改進。此外，分別利用幾種不同強度準則預測了巖石的抗拉強度，通過與試驗數據進行對比，判斷了強度準則預測抗拉強度的適用性。研究結果可以為抗拉強度計算和預測提供一定的科學依據。

1 幾種強度準則

1.1 直線型Mohr-Coulomb準則

Mohr-Coulomb強度準則建立于1900年，直至現在仍然是工程設計的主要依據。該準則是基于巖土材料的剪切破壞提出的，沒有考慮中間主應力的影響，利用莫爾圓來表示應力狀態，其表達式為[2]：

式中：τ為剪應力；c為黏聚力；σ為正應力；φ為內摩擦角。

由式（1）可以推導得到主應力的表達式：

式中：σ1和σ3分別表示最大主應力和最小主應力。

令σ1=0，σ3=-σt，可以得到單軸抗拉強度σt的表達式：

1.2 拋物線型Mohr-Coulomb準則

通過大量試驗發現，巖土材料的包絡線并非是一條直線，因此佘成學等人[3]提出了雙參數的拋物線型M-C準則，具體表達式為：

其中，a、b可以表示為：

式中：σc為單軸抗壓強度。

式（5）可以用主應力表示為：

A和C可以通過線性回歸得到，由此可以計算單軸抗拉強度：

1.3 Griffith強度準則

Griffith強度準則最早出現在材料力學中，用于描述裂紋尖端效應，后來被引入巖土工程中，來描述巖體中微裂隙的擴展。Griffith認為，引起裂紋擴展的應力為拉應力，因此提出了關于拉應力的強度準則[4]：

利用式（9）便可以計算出巖土材料的抗拉強度。

1.4 Hoek-Brown準則

Hoek-Brown準則是在大量試驗基礎上提出的一種經驗準則，狹義表達式為[5]：

式中：m為試驗參數。

令σ1=0，σ3=-σt，可以得到單軸抗拉強度的表達式：

1.5 Lade-Duncan準則

Lade依據于砂土的真三軸試驗結果，在1975年提出Lade-Duncan準則[6]，考慮了中間主應力的影響，并且在1984年進行了進一步修正，使其適用于更多的巖土材料[7]。這里用1984年修正后的L-D準則表達式進行計算：

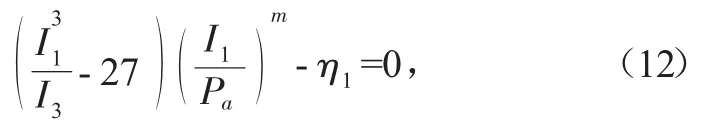
式中：Pa為一個標準大氣壓；η1、m為材料參數；I1、I3分別為第一、三應力張量不變量。

當材料中存在拉應力時，需要加上I1+3αPa，αPa為材料抗拉強度。α為材料參數。通過進行推導得到：

通過進行數值回歸，可以得到材料的抗拉強度。

2 抗拉強度計算

一般計算巖石的抗拉強度有兩種方法，分別為直接拉伸和間接拉伸，由于直接拉伸試驗所需的試樣很難制作，因此目前大多工程和研究均采用間接拉伸法，常用的方法就是巴西劈裂試驗。根據國際巖石力學學會（ISRM）所提到的抗拉強度試驗與計算方法[8]，依據圖1中的幾何關系，得到了彈性力學平面應變問題解析。式（15）表示了A點的應力狀態。

圖1 圓盤應力狀態

在圓心處O點處，θ1=θ2，r1=r2。所以可以將式（15）簡化為：

式中，由于y方向的力是x方向的3倍，所以認為σx=σt。即巖石所受的拉應力為圓心處沿x方向的應力。

3 對比與分析

3.1 抗拉強度計算公式修正

ISRM建議的抗拉強度計算方法將圓盤中心點的水平應力作為抗拉強度，但是大量巴西劈裂試驗現象表明，很多試驗并不是中心起裂，還有其他形態的破裂方式，如圖2所示。并且研究發現，非中心起裂的破壞模式多見于層理發育的沉積巖中，層理巖石的橫觀各向同性特征導致了偏心破裂。此時用式（16）計算得到的抗拉強度與實際有偏差，該情況下抗拉強度的誤差有多大？是否在可接受范圍？基于此，考慮非中心破裂形式，對式（16）進行了修正。

圖2 巴西劈裂試驗的破裂跡線

基于此，考慮到非圓心破壞的破裂面形態，利用幾何數學對破壞跡線進行了分析。假設破裂面為一條半徑為r，弦長為D，圓心角為α的標準圓弧l，如圖3所示。圖中a為弧頂與圓心的距離，由此可以通過圖中的幾何關系得到l。當破裂面沿著直徑D破壞，此時l=D'。

圖3 破裂面的幾何關系圖

由此可以得到弧長，再通過式（18）：

可以得到裂紋為弧線條件下巖石的抗拉強度σt：

式（19）中，a、P可通過試驗直接得到。

以圖2中提到的4個非中心破裂的試驗結果為對象，分別利用式（16）和式（19）計算得到了抗拉強度（表1）。

從表1中可以看出，非中心起裂的抗拉強度要略低于中心點的抗拉強度，并且偏心距越大，強度降低越多。劈裂法測得的是圓心位置的抗拉強度，但是在出現非中心起裂時，實際抗拉強度應分布在破裂跡線上。計算結果表明，在巴西劈裂試驗中，按照傳統方法計算非中心起裂試樣的抗拉強度，其結果偏高。由此可得到一組計算抗拉強度的公式：

表1 修正前后試樣抗拉強度對比

黃耀光等人（2015）[14]研究表明圓盤上的水平應力偏離中心點越遠，其值越小（圖4），本文計算結果符合這一規律。

圖4 巴西圓盤無量綱水平應力

3.2 強度準則適用性分析

為驗證以上強度準則的適用性，以太行山奧陶系泥質灰巖為對象，分別開展了三軸壓縮和巴西劈裂試驗，試驗結果列于表2。

表2 奧陶系泥質灰巖三軸試驗結果

結合張磊等人[15]以及本文的試驗結果，分別利用上述5種強度準則進行計算分析，得到了不同強度準則對比下的應力關系圖，如圖5所示。

圖5 應力關系曲線

通過將試驗數據與計算結果進行誤差對比，可以將擬合情況定量化，利用式（21）進行誤差分析：

表3 誤差分析對比結果

表3中可以看出，在高圍壓條件下，H-B準則是最接近試驗數據的，該結果與劉運思等人[16]的研究結果相符合。其次是Griffith準則，而兩個M-C準則的擬合程度較差，相比于直線型M-C準則，拋物線型的更接近實際數據。由于H-B準則是基于大量試驗數據的經驗準則，并且其中有擬合參數，在本算例中該擬合參數是通過試驗數據擬合得到，所以最終的計算結果與實際最為接近。Griffith準則是針對于抗拉強度提出的強度準則，因此相比于其他強度準則，在計算抗拉強度時更為有效。而L-D準則與其他準則最大的區別是考慮了中間主應力的影響，為三維應力空間狀態，在本文的計算中，以假三軸狀態為背景，認為中間主應力與最小主應力相等，因此其最終的計算結果會有較大的偏差。而M-C準則，作為最早的強度準則，更多地考慮巖土材料的剪切破壞，不適用于計算拉張破壞，而Griffith準則更適用于低圍壓條件。

Griffith強度準則是基于裂隙擴展提出的巖石抗拉準則，其中不考慮剪切行為，巖石裂隙發育貫通是造成巖石受拉破壞的本質因素，這個結果解釋了地表出露高陡灰巖邊坡豎直拉張節理發育現象。而H-B準則是巖石抗剪強度準則，拉張破壞本質上是剪切破壞的一種特殊情況，沒有考慮裂縫的擴展。在高圍壓下，巖石以剪切破壞為主，主要發生塑性變形。因此深部巖體潛在剪切面通常是連續的，并且具有較好的延伸性，常發生大型斷裂、斷層、深層滑動等。而淺表層巖體多出現短小的節理，以豎直方向為主，將巖體切割成大量塊體，常形成崩塌落石、楔形體滑動等。

4 結語

通過利用不同強度準則計算巖石的抗拉強度，得到了以下認識：

a）通過總結大量巴西劈裂試驗發現，巖石出現3種形式的破裂跡線：非貫通跡線、直線型貫通跡線、非直線型貫通跡線，造成這種現象的主要原因是巖石自身的橫觀各向同性。

b）圓盤的抗拉強度沿著水平方向自圓心向兩側逐漸降低，直觀表現為非中心起裂的試樣抗拉強度較低。利用本文提出的修正公式可以計算得到相應的抗拉強度。

c）通過對比5種強度準則，發現在高圍壓條件下，Hoek-Brown強度準則在預測抗拉強度時，與試驗結果有較好的擬合度，低圍壓條件下，Griffith準則更為適用。傳統的Mohr-Coulomb準則不適用于預測巖石抗拉強度。