利用梯度結構張量刻畫碳酸鹽巖縫洞體邊界

張 晟 李亞林 肖又軍 鄭多明 袁 源 馮 磊

(中國石油塔里木油田公司勘探開發研究院，新疆庫爾勒 841000)

0 引言

塔里木盆地廣泛發育碳酸鹽巖儲層，其中縫洞體是油氣勘探、開發的重要目標之一，通常是由相互連通的洞穴、次生溶蝕孔洞和裂縫組成的油氣儲集體。由于溶蝕作用的非均一性，碳酸鹽巖縫洞體的發育規模、空間形態以及油氣富集程度差異非常大，再加上復雜的地表條件、埋深極大等因素，給油氣勘探和開發帶來很大困難。因此，準確地刻畫碳酸鹽巖縫洞體邊界是碳酸鹽巖縫洞型儲層量化雕刻的重要工作之一。

近年來，許多地震屬性刻畫方法在碳酸鹽巖儲層預測中均取得不錯的效果，包括相干、曲率、螞蟻體、振幅變化率等，而目前較理想的刻畫碳酸鹽巖縫洞體邊界的方法則是由圖像處理領域引入地震解釋領域的GST屬性技術。

在圖像處理領域，描述數字圖像結構的局部方向特征時首次提出GST的概念[1-2]并逐步成為研究熱點，其應用包括不同目標紋理單元的檢測、自適應的多維度濾波等[3-4]。Randen等[5-6]利用三維地震數據的GST提取地震數據的不連續性描述斷層發育特征。Bakker[7]將GST系統地引入地震解釋領域，廣泛用于提取地震數據結構以及地層特征，在斷層自動識別、河道刻畫等方面獲得良好效果。Luo等[8]將GST矩陣構造過程的三維高斯低通濾波函數轉化為由復地震道瞬時能量作為加權值的數據自適應低通濾波方法，有效提高了傾角和方位角估算結果的空間一致性。隨著GST技術的深入研究與應用，大量關于優化GST的相干體技術在地震解釋領域獲得了良好效果[9-10]。陳強等[11]利用GST矩陣特征值計算Chaos和邊緣屬性，精細描述與解釋了不同類型的采空區。問雪等[12]利用地震圖像的GST特征設計結構導向平滑濾波器，在壓制噪聲的同時有效保留了斷層的不連續信息，為斷層識別提供了高質量地震資料。王清振等[13]基于GST的不連續性檢測技術識別鹽丘邊界與斷層，與常規地震屬性方法相比，在巖鹽廣泛發育地區能更好地甄別由高陡地層引起的不連續假象。彭達等[14]根據GST求取傾角信息，再通過構建梯度相關矩陣計算局部地震數據的梯度能量熵值，可以刻畫三維地震數據的不連續空間結構特征，從而增強不連續邊界的清晰度、提高斷層邊界的連續性。崔正偉等[15]結合構造導向濾波與GST相干算法，精細識別了儲層裂縫。王震等[16]利用GST的第二特征值刻畫斷溶體邊界。

中國業界利用GST刻畫碳酸鹽巖縫洞體邊界的應用相對較少。為此，基于前人的GST技術方法，本文針對GST屬性的詳細計算方法及其幾何意義，分析各計算環節對計算結果的影響，以期為碳酸鹽巖縫洞型儲層量化雕刻提供參考。

1 技術原理分析

傳統的圖像處理中濾波與邊緣檢測主要針對相對簡單的鄰域范圍，即被不連續區域分開的均質區域通常僅呈現圖像數值的高、低差異。然而，除了圖像數值的高、低差異之外，某個局部鄰域范圍內依然可能會包含一種模式或類型，如果這種模式具備某種有規律的結構特征，則稱之為紋理。如果用參數描述這些紋理特征則需要進一步明確與簡化，而紋理可以由線性結構組成。N維空間的線性結構定義為至少在一個方向是位移不變的，但并不包括所有方向是位移不變的。由此可見，地震數據的層狀沉積結構特征滿足線性結構定義，因此可以利用GST分析地震數據的結構特征，并由參數化提取用于地震解釋。

地震解釋領域中結構張量矩陣通常由地震數據的梯度構建，為了明確計算過程細節以增強該項技術方法的可復制性，本文將詳細分析與探討各關鍵計算步驟。

以三維地震數據GST屬性計算為例，共分三個步驟：①求取地震數據的梯度；②構建結構張量矩陣，并對張量矩陣的元素分別平滑或積分；③特征值分解并進行排序。

通過對三維地震數據分別在垂直、Inline與Crossline三個方向求取一階偏導數g1、g2、g3，便可得到原始三維地震數據對應的每個數據樣點位置的梯度矢量

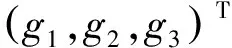
(1)

g不能直接構建張量矩陣求解特征值，因為直接構建的張量矩陣

(2)

的秩不大于1，即使對g1、g2、g3分別進行平滑再構建張量矩陣也是如此。

當Tgrad的元素均不為零時，Tgrad的三個特征值λ1、λ2、λ3中只有一個不為零(如λ1≠0，λ2=λ3=0)，則

(3)

本文稱λ1為梯度的能量。

構建結構張量矩陣包含兩個關鍵步驟：首先利用梯度與其轉置相乘形成3階方陣(也稱為并矢積)；其次對方陣中每一個元素分別平滑(或稱局部平均)，得到一定尺度范圍內平均的結構張量矩陣[17]

(4)

式中〈·〉表示對角括符內的對象平滑，通常采用高斯濾波的方式。由張量矩陣的對稱性可知，只需進行6個元素的平滑即可完成對9個元素的平滑。如果對g1、g2、g3也進行平滑，則總共需要9個三維數據體的平滑計算。對梯度元素的平滑計算可以壓制由地震噪聲引起的局部梯度異常，從而增強后續計算的魯棒性；對張量元素的平滑計算使張量矩陣不僅包含最大梯度能量方向的特征，并且還包含所有正交方向的變化特征。

高斯濾波器在低通濾波或者平均計算等方面優點很多且應用廣泛，高斯核函數卷積平滑計算的本質為局部尺度范圍內的加權平均，通常一維高斯函數定義為

(5)

式中：σ為標準差，用于表征高斯函數的半寬度；t為采樣點數。

圖1為σ=1的高斯函數。可見，距離中心樣點越遠則權重值越小，當|t|>4時權重值趨近于零。確定一個非負σ值時，濾波器的有效長度可近似截斷為-4σ≤t≤4σ。當濾波器有效長度較小(σ<3)時，宜直接進行卷積計算；當濾波器的有效長度較大時，可采用遞歸高斯濾波有效提高運算效率[18]。文中的高斯濾波方式均采用有效長度內的離散樣點進行卷積計算，即當給定σ為某一正整數時，取有效離散采樣點數為8σ+1。對于三維地震數據而言，卷積的方式分為兩種，第一種是利用三維高斯核函數直接計算一個三維空間卷積核，另一種則是沿垂直、Inline與Crossline三個方向分別進行一維高斯濾波器的卷積，兩種方式均可實現同樣的目標。

圖1 σ=1的高斯函數

由于構建的張量矩陣是實對稱矩陣，屬于半正定二次型，因此具有三個非負特征值，且對應的三個特征向量兩兩正交。對每個數據樣點處的結構張量矩陣特征分解能夠得到表征圖像結構的各向異性參數與方向特征[19]。對于任意三維數據的結構張量矩陣而言，其特征分解均可表示為[20]

T=λ1uuT+λ2vvT+λ3wwT

(6)

式中：λ1≥λ2≥λ3≥0按大小順序命名為第一、第二和第三特征值；u、v和w分別為λ1、λ2和λ3對應的單位特征向量，稱為第一、第二和第三特征向量。對常規三維地震數據而言，通常u的方向垂直于反射同相軸的局部平面，v、w位于反射同相軸的局部平面內，并且v、w表征橫向不連續變化方向，如由斷層或者河道反射特征引起的地震數據變化。由于λ1、λ2和λ3分別反映對應方向的變化特征，因此通過優選三個特征值及其不同組合計算地震數據紋理類屬性，便可解釋目標地質體。在以河道及斷層為研究目標時，u垂直于沿反射同相軸解釋的空間曲面，v在局部范圍內垂直于河道和斷層走向，而w則呈局部平行的規律。對于碳酸鹽巖縫洞體而言，河道及斷層響應均屬于不連續異常反射，而縫洞體引起的強反射異常區域在三維地震數據體中呈復雜三維空間立體結構的不連續變化，在局部三維空間尺度內沿各個方向均有振幅變化，因此λ1反映主要的層狀反射特征，λ2和λ3刻畫了縫洞體反射異常區域，類似于沿不同的視角對一個三維立體結構成像。由于特征值無量綱，因此在刻畫目標縫洞體時閾值選取便成為一個不可避免的問題。

2 實際應用測試

2.1 二維GST屬性分析

為了驗證不同平滑方案的影響，選取塔里木油田塔北A區典型地震剖面(圖2)計算二維GST屬性，以識別碳酸鹽巖縫洞體異常區域及其外部輪廓。

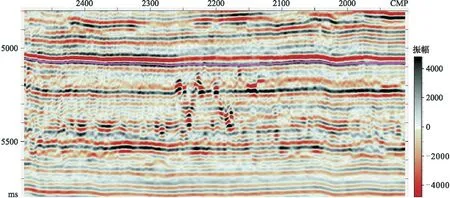
圖2 塔北A區典型地震剖面

根據GST屬性計算方法可知，在二維情況能求解兩個特征值，針對該地震剖面進行以下測試：①不做任何平滑，直接利用梯度構建結構張量矩陣進行特征值分解；②對梯度元素平滑；③對張量元素平滑；④對梯度元素及張量元素均平滑。平滑計算會對分解結果的值域產生一定影響，故采用歸一化策略將最終結果的值域調整為0～100再進行對比、分析，實際計算結果均表現為高值分布較少(90%以上均小于20)，故色標顯示范圍調整為0～20。

圖3為不做任何平滑及對梯度元素平滑求解的λ1。可見，λ2=0，λ1反映了地震數據梯度的能量，僅對梯度元素平滑表現出低通濾波效果(圖3b)，λ1并不能刻畫碳酸鹽巖縫洞體邊界。

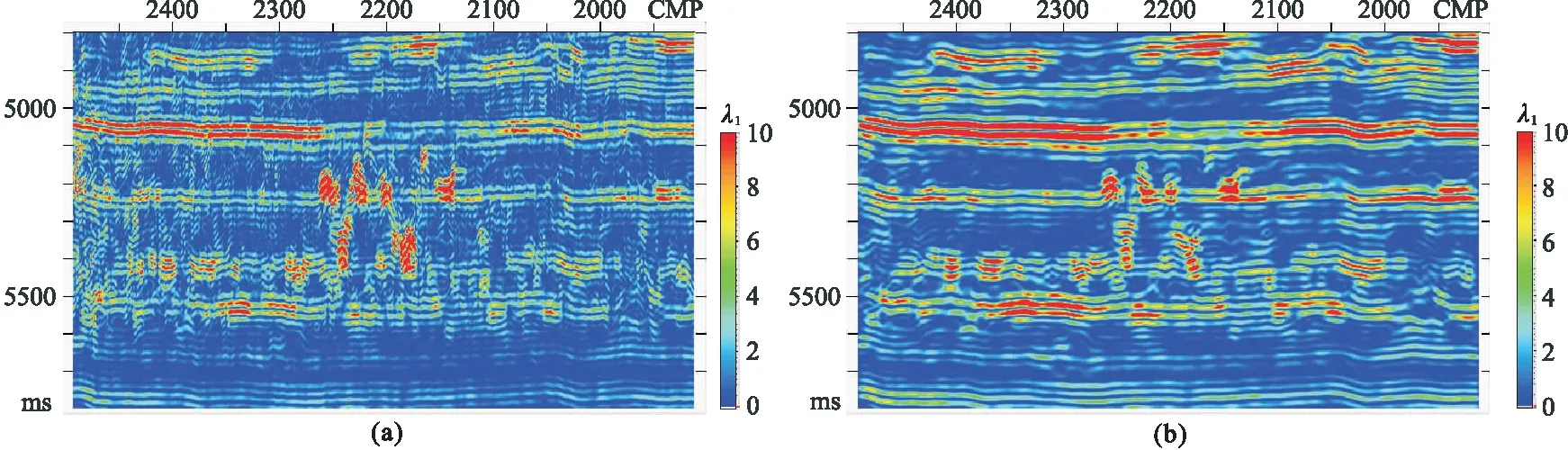
圖3 不做任何平滑(a)及對梯度元素平滑(b)求解的λ1

圖4為對張量元素平滑求解的λ1及λ2。可見：λ1主要反映了地震數據層狀反射的主要結構特征，由于縫洞體區域的地震剖面依然具有垂直方向的反射振幅變化，因此在層狀結構特征的背景上還存在縫洞體反射特征(圖4a)；λ2與碳酸鹽巖縫洞體反射異常區域一致性較高，且不受層狀結構特征影響，將顯示色標選取確定的閾值進行低值截取，可自動刻畫碳酸鹽巖縫洞體邊界(圖4b)。

圖5為對梯度元素及張量元素均平滑求解的λ1及λ2。可見，整體特征與圖4基本一致，局部細節部分有細微差異，但對縫洞體邊界刻畫影響較小，梯度元素平滑對背景噪聲具有一定壓制作用。

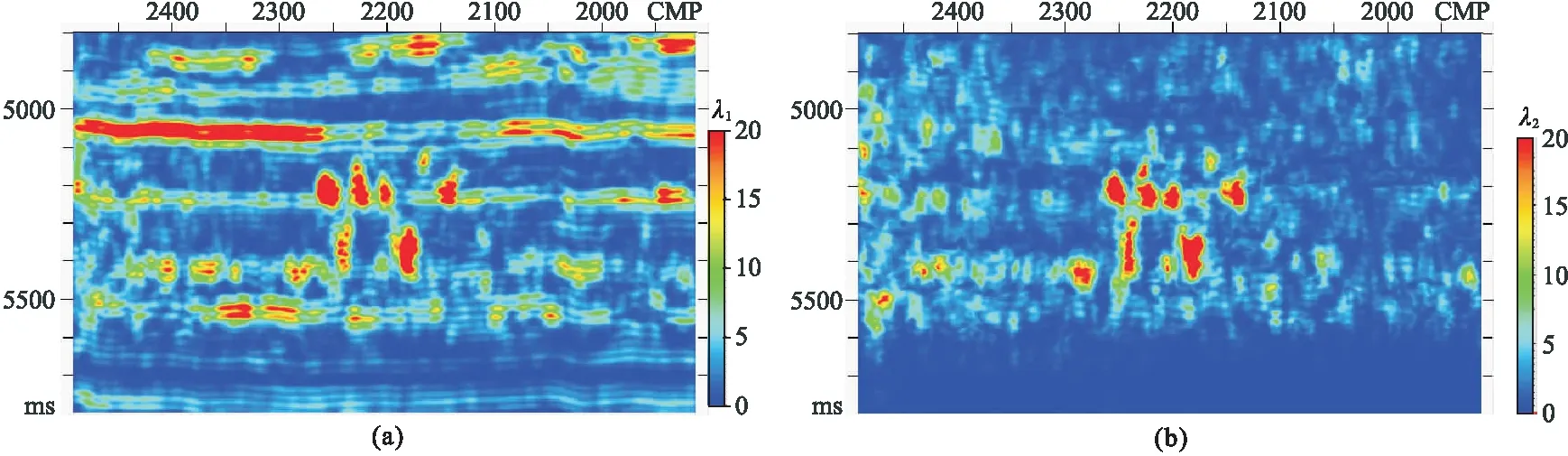
圖4 對張量元素平滑求解的λ1(a)及λ2(b)

圖5 對梯度元素及張量元素均平滑求解的λ1(a)及λ2(b)

2.2 三維GST屬性分析

在塔北A區切取5km×5km的三維地震數據計算GST屬性。圖6為對梯度元素及張量元素均平滑的三維GST求解結果。將顯示色標選取一定的閾值進行低值截取，其中λ2(圖6c)與λ3(圖6d)的動態顯示范圍相同，即使顯示范圍較大，λ3依然反映了縫洞體異常反射區域的特征(圖6d)。由于λ3的整體值域約為λ2的一半，因此將λ3的顯示范圍減小一半(圖7)，此時λ3與碳酸鹽巖縫洞體異常反射區域對應較好，與λ2整體特征(圖6)相似但細節差異明顯，表現為不同的觀測視角。

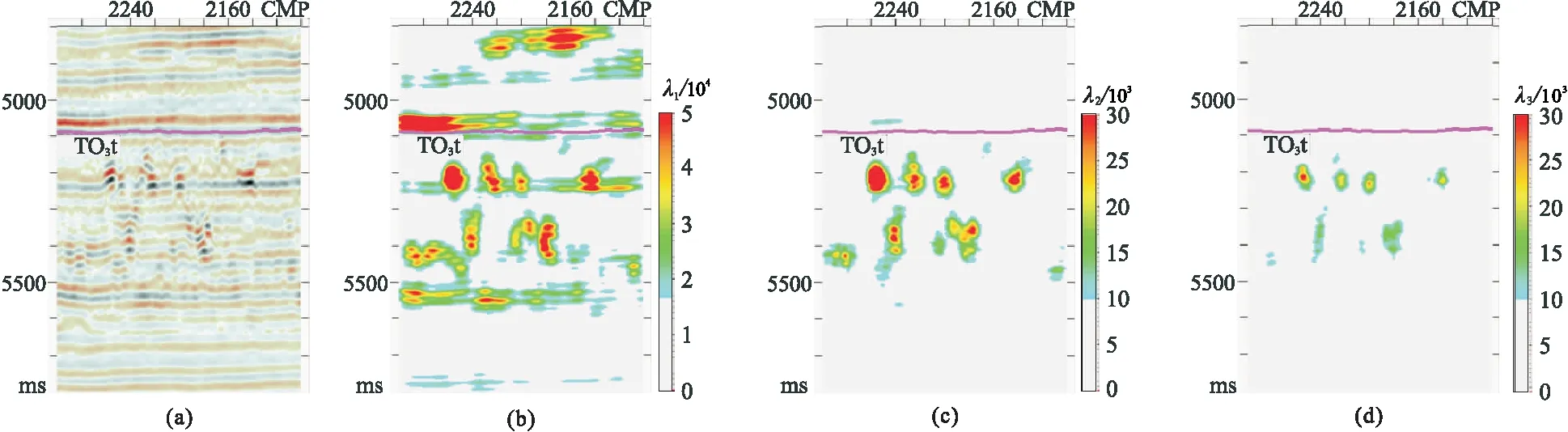
圖6 對梯度元素及張量元素均平滑的三維GST求解結果

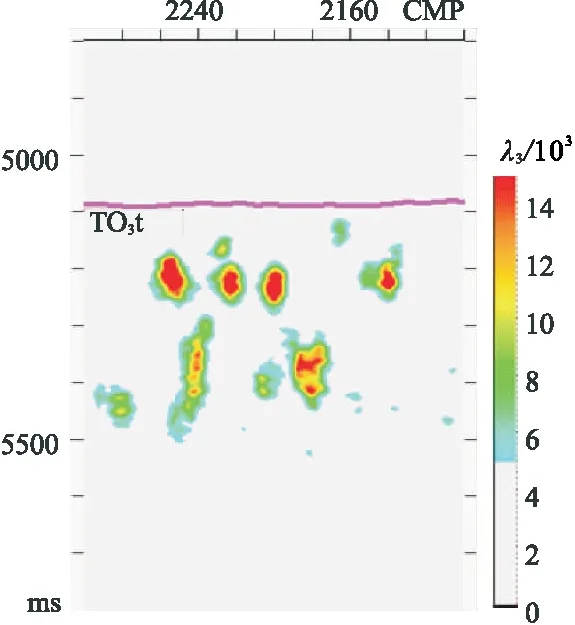
圖7 將圖6中λ3的動態顯示范圍調整為λ2的一半的結果

為了進一步明確λ2與λ3對平面刻畫的差異，對解釋層位(TO3t)向下取相同的時窗(300ms)分別計算λ2與λ3的均方根(圖8)，可見λ2(圖8a)與λ3的均方根(圖8b)也表現出整體相似但又有差異的現象。切取一條盡量穿過所有平面屬性高值異常區的任意線地震剖面(圖9)、λ2剖面(圖10)與λ3剖面(圖11)，可見后兩者在一定的低值截取與顯示動態范圍內有效刻畫了前者的形態各異的碳酸鹽巖縫洞體反射異常，且較符合碳酸鹽巖縫洞體溶蝕規律，但在不了解縫洞體真實空間形態的情況下，很難判斷λ2、λ3或兩者的組合計算結果的客觀性。

圖8 沿TO3t向下取300ms的λ2(a)與λ3(b)的均方根

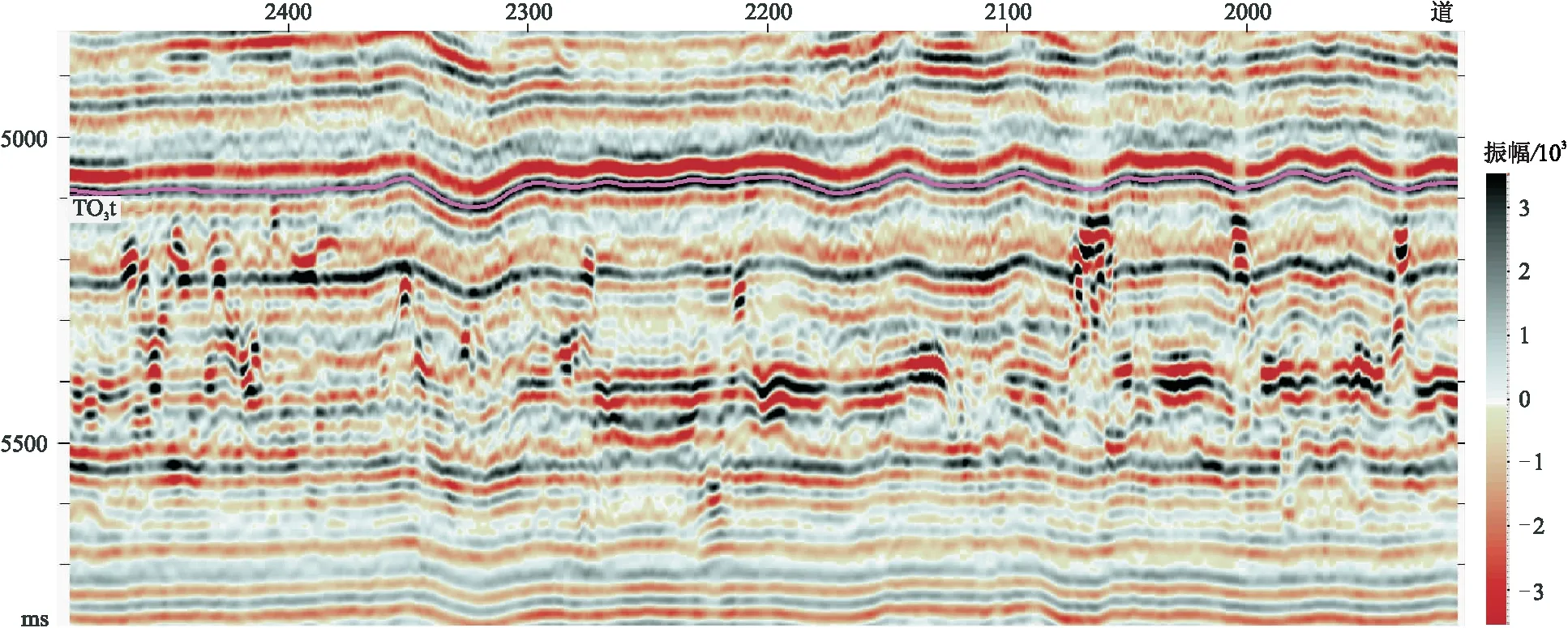
圖9 穿過所有平面屬性高值異常區的任意線地震剖面

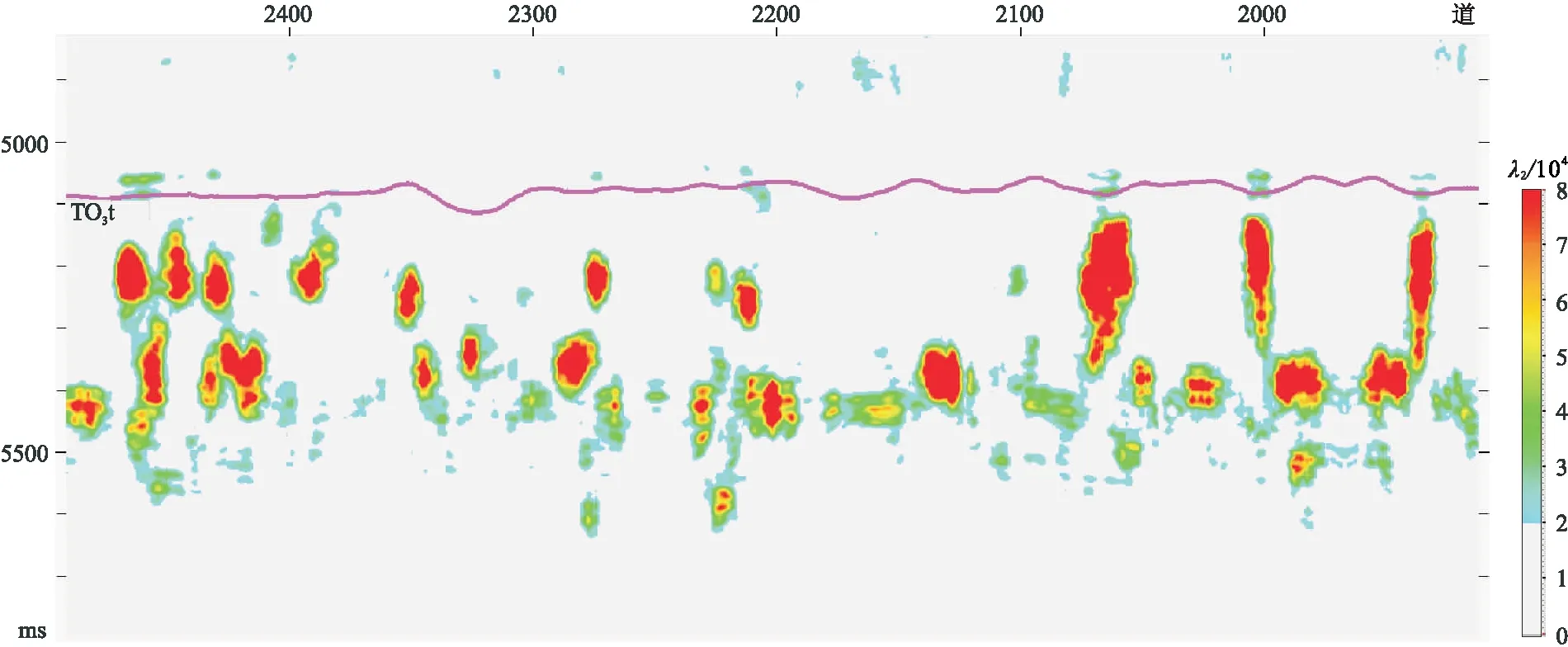
圖10 穿過所有平面屬性高值異常區的任意線λ2剖面

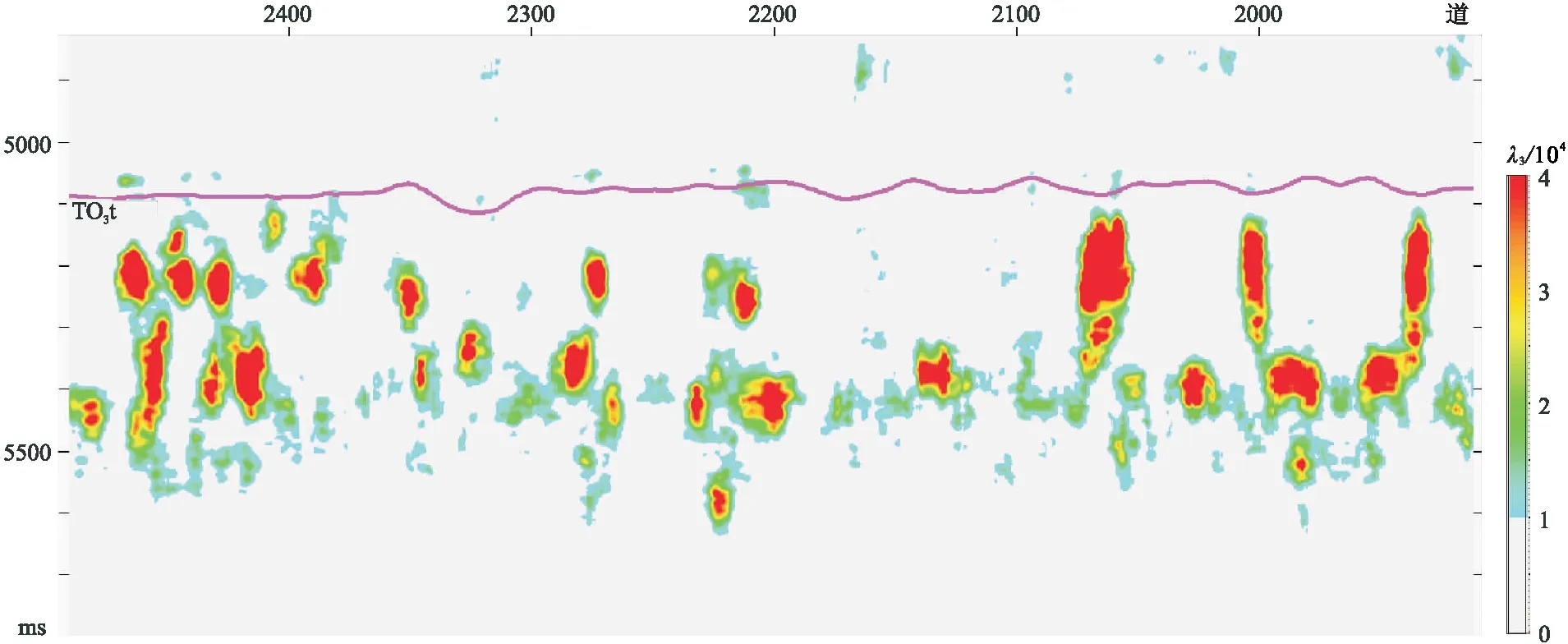
圖11 穿過所有平面屬性高值異常區的任意線λ3剖面

對實際生產應用而言，可以考慮利用工區鉆井資料作為驗證信息進行統計、分析，優選λ2、λ3或兩者的組合計算結果作為碳酸鹽巖縫洞體邊界刻畫的敏感地震屬性，從而降低儲層預測的多解性。

3 閾值選取策略

通過GST矩陣求解得到的特征值為無明確物理量綱的數值，不具有明確的地質意義，如果僅僅根據經驗選取儲層的刻畫閾值則依然屬于定性描述范疇。實際應用中可采用鉆時曲線交會分析確定儲層刻畫閾值的選取依據，也可采用氣測顯示、放空、漏失深度等信息標定鉆遇儲層邊界以選取閾值，實質均為利用實鉆信息判斷鉆遇碳酸鹽巖儲層位置，從而截取低值與控制顯示動態范圍，不失為一種合理的閾值選取策略。

由計算原理可知，在縫洞體異常區域特征值數值的高低與儲層發育程度并無明確的映射關系，并且計算結果受地震資料信噪比、平滑尺度參數等多重因素影響。此外，在同一工區選擇不同的鉆井信息選取閾值時通常會出現閾值不一致的情況，因此直接利用GST屬性不能定量刻畫碳酸鹽巖縫洞體。為了區別定性描述與定量刻畫，本文提出標尺定量的概念，標尺定量即為無量綱的地震屬性以實鉆信息作為標尺而賦予刻畫閾值的意義。對于定性刻畫來說，標尺定量可以有效降低縫洞體刻畫的多解性，不同的鉆井數據作為標尺可能存在刻度差異，可以采取統計優選、平均計算以及多重約束的策略選取最終采用方案。

塔北A區有A、B、C、D、E等 5口鉆井，采用歸一化將得到的λ2、λ3的值域控制在0～1000。圖12為C井鉆時曲線與氣測(全烴，TG)曲線交會圖。可見，鉆至6430m深度處鉆時降為0，發生放空且漏失鉆井液，TG曲線值達到1.8%，因此C井于該深度處鉆遇縫洞體。沿C井軌跡抽出λ2、λ3曲線(圖13a)，兩者的整體相似性較高，但縫洞體位置對應λ2=38、λ3=33(圖13b)——C井的兩個標尺刻度值。以同樣的方式統計其余鉆井的標尺刻度值(表1)，可見每口井的標尺刻度并不一致。設定x1與x2兩個權重系數和期望閾值k，構造線性方程組

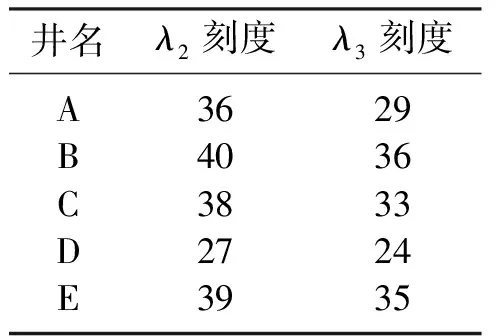
表1 塔北A區鉆井標尺刻度值統計

MX=K

(7)

其中

式中λ2，i、λ3，i的i=A,B,C,D,E代表井號。式(7)為超定方程，設定k=50，利用最小二乘法求解得到x1=1.8107，x2=-0.5099。利用公式

λ=x1λ2+x2λ3

(8)

得到λ2、λ3的線性組合結果，并將整個三維體范圍計算結果作為最終刻畫縫洞體的特征值屬性。圖14為過C井剖面特征值計算結果。可見，線性組合的結果λ(圖14d)融合了λ2(圖14b)與λ3(圖14c)的細節特征，設定的期望閾值與地震反射特征(圖14a)、鉆井信息(圖12、圖13)高度吻合。圖15為塔北A區縫洞體刻畫平面圖，顯示該區西部發育的斷裂帶與縫洞體分布一致，結合標尺定量獲得的最終刻畫閾值與λ2、λ3的線性組合結果(圖14d)可以有效解決不同鉆井標尺刻度不一致的問題。

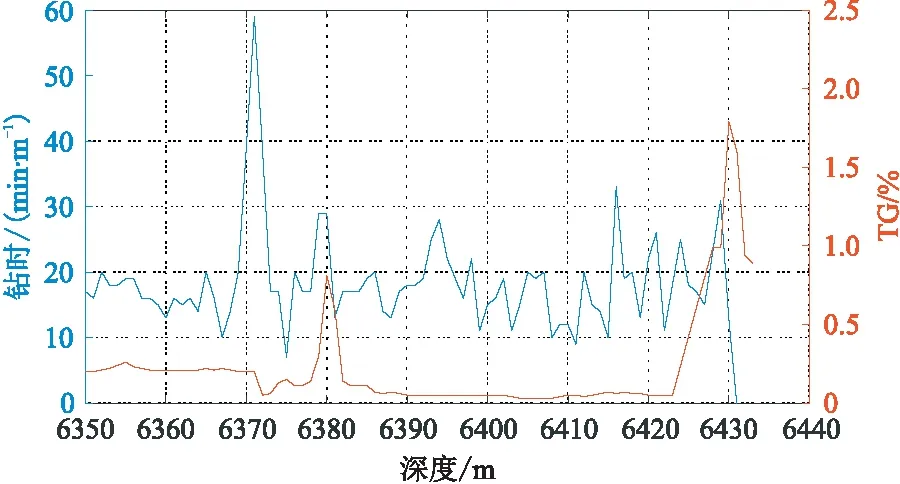
圖12 C井鉆時曲線與氣測曲線交會圖

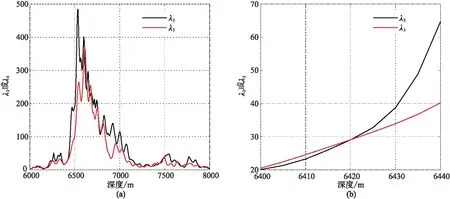
圖13 C井λ2與λ3曲線(a)及其縫洞體位置局部顯示(b)

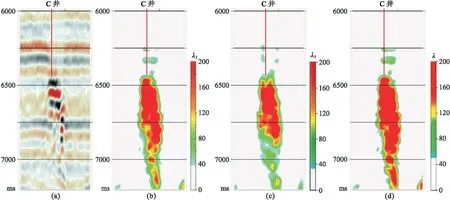
圖14 過C井地震剖面及特征值計算結果

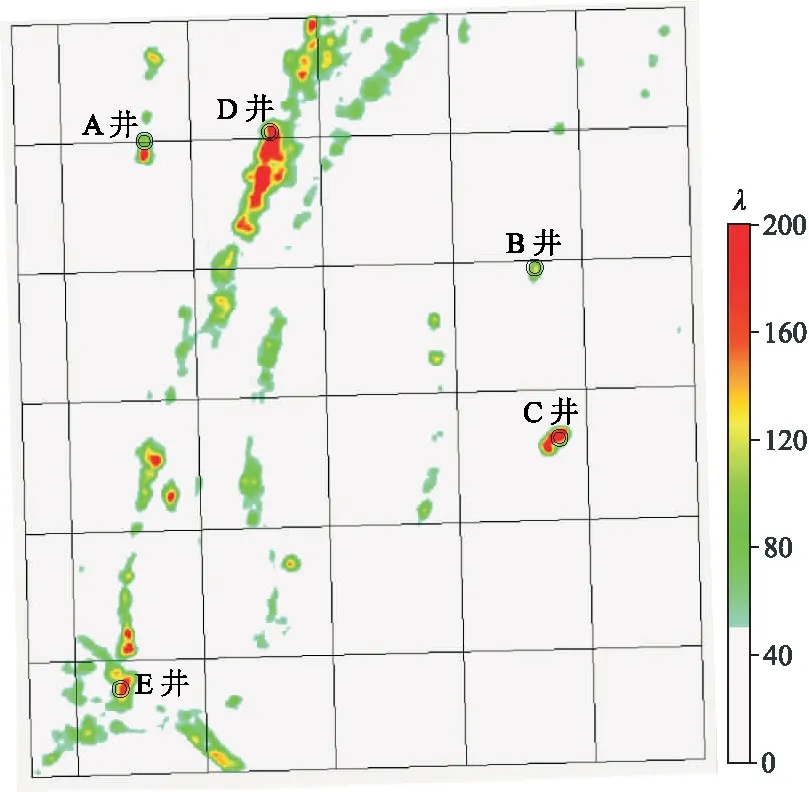
圖15 塔北A區縫洞體刻畫平面圖

4 結論

梯度結構張量屬性可更連續地刻畫碳酸鹽巖縫洞體，通常還能在一定程度上反映溶蝕規律。技術原理分析及實際地震資料測試表明：

(1)對張量元素的平滑計算是整個技術的關鍵，使結構張量矩陣不僅包含最大梯度能量方向的特征，并且還包含所有正交方向的變化特征，而梯度元素的平滑對背景噪聲具有一定壓制作用，可以提高最終計算結果的信噪比。

(2)第二特征值與第三特征值對碳酸鹽巖縫洞體均具有一定刻畫能力，反映了不同觀測視角的縫洞體三維空間形態特征，并且刻畫結果較符合碳酸鹽巖縫洞體溶蝕規律。結合實際研究區地質認識，優選或組合第二與第三特征值屬性，在合適的低值截取與顯示范圍內可以有效刻畫碳酸鹽巖縫洞體邊界。

(3)本文提出了一種利用鉆井信息作為標尺刻度無量綱特征值的方案，求解的特征值線性組合結果本質上是研究區基于鉆井信息的多重約束解，融合了第二與第三特征值的細節特征，并且有效解決了不同鉆井刻度值不一致的問題，但標尺定量刻畫不是完全定量刻畫。