飛機變壓整流器健康管理算法研究

李一卓， 高朝暉*， 郗 展， 王 爽， 李小寧， 梁源頎

(1.西北工業大學 自動化學院，陜西 西安 710129； 2.航空工業洛陽電光設備研究所，河南 洛陽 471000)

隨著飛機機載用電設備的增加和電力電子設備在飛機電力系統中的廣泛應用，總用電功率和電能種類的需求也日益增加，飛機供電系統需滿足更高的性能要求[1]。此外，電力系統中的諧波問題的加重也威脅著飛機的安全運行，現階段降低諧波方法主要是采用多脈波整流技術，飛機電氣系統多采用12脈波變壓整流器(Transformer Rectifier Unit，TRU)，將115 V/400 Hz主交流電源轉換成28 V低壓直流電。變壓整流器對飛機電氣系統有重要的作用，但隨著使用時間的增加，變壓整流器各部件的老化問題也影響飛機的安全運行。

目前，系統維保技術以事后維修和針對性預防維修等為主，這些方式耗費資源，且效率低下。如何有效地提高飛機的安全性能，保障飛機安全飛行并降低維護費用，成為航空領域至關重要的問題[2]。因此故障預測與健康管理(Prognostics and Health Management,PHM)技術應運而生，成為提高飛機安全可靠性和經濟性的主要方法。健康管理技術利用先進的傳感器技術，對系統的狀態信號進行監控，并利用智能算法，對系統健康狀態做出判斷，在系統因老化引起異常之前制定應對方案，從而避免系統因異常造成的損失，提高系統運行的安全可靠性[3]。

隨著多電與全電飛機的出現和發展，飛機電源系統的安全性與可靠性越來越重要，而變壓整流器作為二次電源的重要組成部分，其發生故障所帶來的影響對飛行安全具有嚴重影響。將健康管理技術研究應用于航空變壓整流器，實時監測變壓整流器健康狀態，從而對變壓整流器進行及時維護，避免其因老化引發的故障，減少損失，具有重要的現實意義與經濟意義。

針對以上問題，以隔離式12脈波航空變壓整流器為研究對象進行健康管理算法研究。在對12脈波變壓整流器的組成和原理進行分析的基礎上，確定變壓器繞組和電容為系統健康評估的關鍵部件，分別對電容和繞組進行老化特性研究；搭建了變壓整流器的老化等效模型，采用蒙特卡羅分析方法，通過大量仿真數據，確定出變壓整流器三相輸入電流有效值、輸出電壓平均值和直流畸變系數作為系統老化特征參數，來進行系統狀態評估；采用高斯混合模型建立了變壓整流器健康基準模型，計算出系統不同老化階段的特征參數與基準模型間的馬氏距離，根據馬氏距離進行分類，分別確定出變壓整流器繞組和電容的老化狀態；最后通過訓練BP神經網絡實現對變壓整流器的健康狀態的評估。

1 變壓整流器結構分析與關鍵器件的確定

1.1 變壓整流器基本結構

12 脈波變壓整流器的電路結構圖如圖1所示，主要由移相變壓器、三相整流橋、平衡電抗器、電容、電感和負載組成，12脈波變壓整流器輸入額定電壓為三相115 V/400 Hz 交流電、輸出額定電壓為DCVd=28 V、輸出額定電流為Id=30 A。移相變壓器由輸入的三相電源給一次側星形連接繞組供電，經過由變壓器二次側星形連接繞組和三角形連接繞組連接兩組整流橋，兩組整流橋輸出正端連接平衡電抗器。

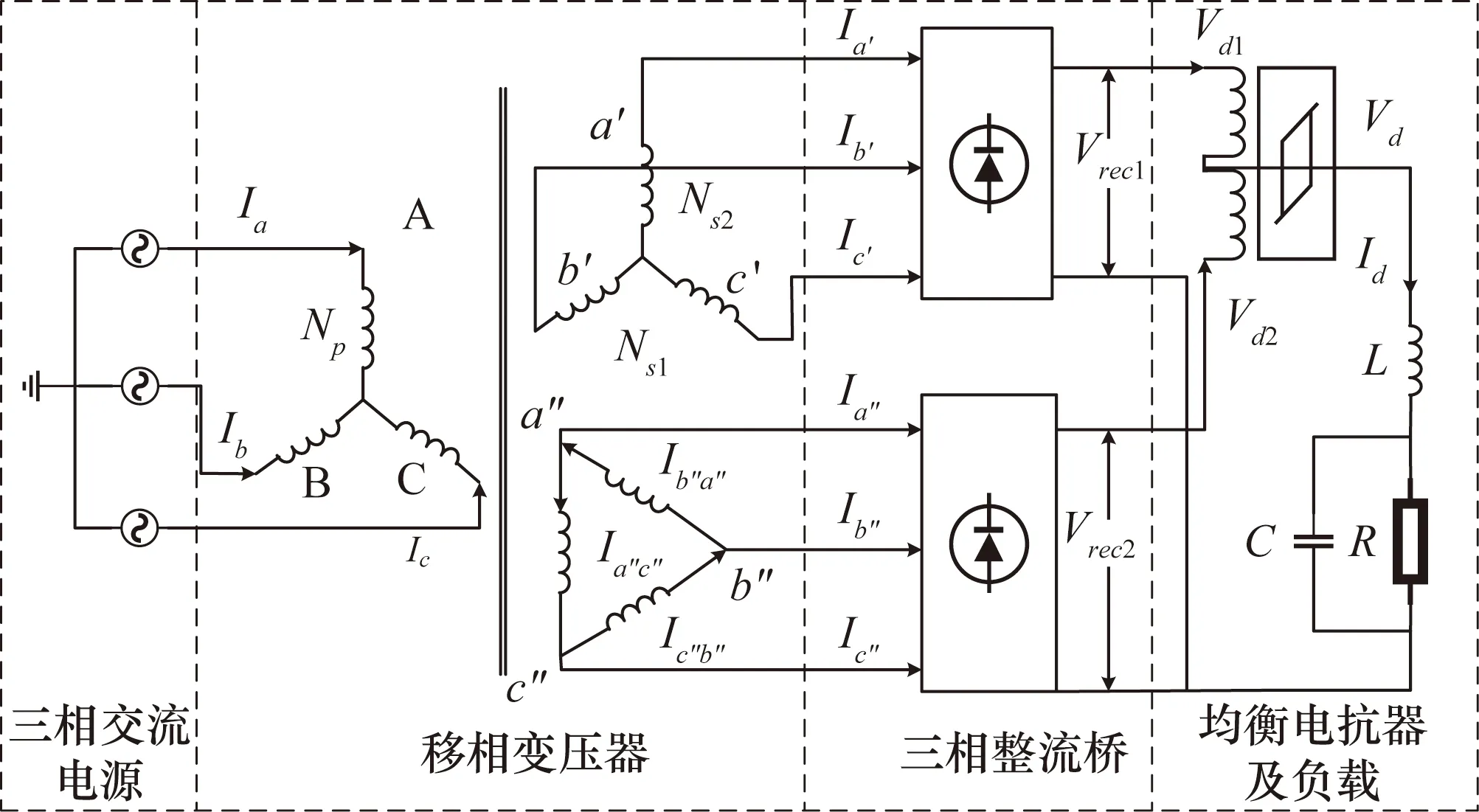
圖1 變壓整流器的結構圖

1.2 關鍵器件的確定

在對變壓整流器進行健康狀態評估時，如果考慮所有部件會影響健康狀態評估的效率效果,要合理選擇健康狀態評估的監測部件。由于系統關鍵部件是變壓器，且相關文獻對多年來變壓器發生故障的記錄研究表明，近80%的故障歸因于繞組匝間短路[4-5]，這些匝間短路故障的原因是繞組絕緣退化或磨損導致相鄰繞組短路。大量研究也表明，多數電力電子電路的性能退化是由于電路中元器件的失效所引起，在典型工作條件下，電解電容失效率高達60%，MOSFET(Metal-Oxide-Semiconductor Field-Effect Transistor，金屬一氧化物半導體場效應晶體管)失效率為31%，電感器件失效率為6%，二極管失效率為3%[6]，在充分調研后，得知變壓整流器輸出濾波電容可能由于電解液泄露導致電解液減少，導致輸出電壓紋波變大，因此把電容也列入監測對象。通過仿真表明，隨著絕緣繞組的等效電阻與電容的電容值和等效串聯電阻值的變化，系統輸出特性隨之變化，因此變壓整流器的健康狀態評估關鍵部件選擇變壓器繞組和輸出濾波鋁電解電容，通過健康狀態評估算法對變壓器繞組絕緣和鋁電解電容老化狀態進行實時判斷。

2 變壓整流器系統外部特征參數的選擇

由于TRU絕緣繞組以及電容的老化特性參數在工作中不易測量，只能通過可測量的外特性來對系統進行狀態評估。在變壓整流器系統中可測得的外特性參數有：三相輸入電流的有效值Irms和ITHD，輸出電壓的均值Vave、電壓紋波Vpeak和直流畸變系數df。

2.1 繞組絕緣外部特征參數的選擇

在考慮絕緣介質材料的電性能時，一般按照圖2所示的等效并聯電路來研究繞組絕緣老化[7]。

其中等效電容Cp的公式如下[7]：

Cp=εrC0=εrε0S/d=2πrεrε0ω/d

(1)

式中：ε0=8.85×10-12F/m為真空介電常數；εr為相對介電常數，取值2.6 F/m；r為繞組的平均半徑；ω為繞組絕緣寬度；d為相鄰兩匝線圈的間距。計算得Cp=3.6 nF。

通過以下公式計算兩個相鄰匝之間的絕緣等效電路中的電阻Rp：

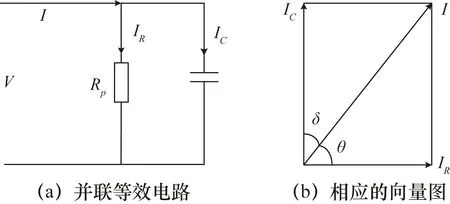
圖2 絕緣介質的等效電路

(2)

式中：ω=2πf，f為施加的電壓頻率；δ為損耗角，表示絕緣中的介質損耗。繞組絕緣完好時介質損耗為0.006[8]，計算得Rp=1.85×107Ω。

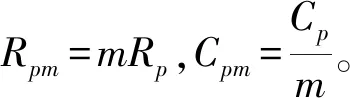
由于等效電容的值Cpm基本不變，需修改等效電阻值Rpm以表示不同退化水平的絕緣繞組。繞組絕緣完好時Rpm值為3.7×107Ω，將Rpm值從3.7×107Ω減小到10-5Ω，發現當等效電阻大于1 Ω時，各參數沒有明顯的變化，隨著變壓器內部繞組進一步老化，TRU輸出電壓平均值降低、紋波和直流畸變系數增大、輸入三相電流有效值增大、輸入電流減小，且電流有效值變化最大，則可通過電流有效值變化量判斷繞組老化相位，當等效電阻小于0.01 Ω時，輸入電流變化幅度很大，繞組絕緣已經嚴重老化。

因此研究絕緣等效電阻在[0.01,1] Ω時的變化趨勢，A相電流有效值在[0.01,1] Ω內變化趨勢如圖3所示，TRU輸入A相電流額定有效值為2.75 A，當等效電阻值小于0.01 Ω時，初級側輸入電流大于3倍額定電流，變壓器絕緣處于極度惡劣的情況；當等效電阻值等于0.03 Ω時，初級側輸入電流約為2倍額定電流，如圖中點B所示；當等效電阻值小于0.1 Ω時，初級側輸入電流大于1.2倍額定電流，如圖中點A所示；當等效電阻值大于1 Ω時，初級側輸入電流非常接近變壓器額定值。因此可認為當等效電阻值在[0.01,1] Ω范圍內時，初級側輸入電流在額定電流和3倍額定電流之間變化，這表明變壓器繞組絕緣出現了老化。

在Saber模型中，可以用蒙特卡羅分析法來獲取數據，其采用均勻分布的賦值方法以″uniform(a,b)″的形式完成，其中a為取值范圍中心值，b為變化比例，參數的變化范圍為(a-ab,a+ab)，通過大量外部數據來模擬系統實際老化進程，對繞組絕緣從完好到老化進行仿真，將參數分為表1所示的4個等級。

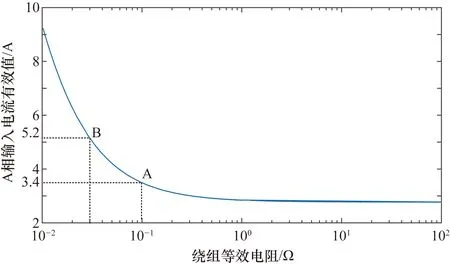
圖3 A相電流有效值變化趨勢

表1 絕緣老化不同階段等效電阻取值范圍

模擬滿載情況下變壓器原邊和副邊A相繞組2匝繞組間絕緣老化，等效電阻Rpm取不同值時的各參數變化趨勢的仿真結果如圖4(a)和圖4(b)所示。

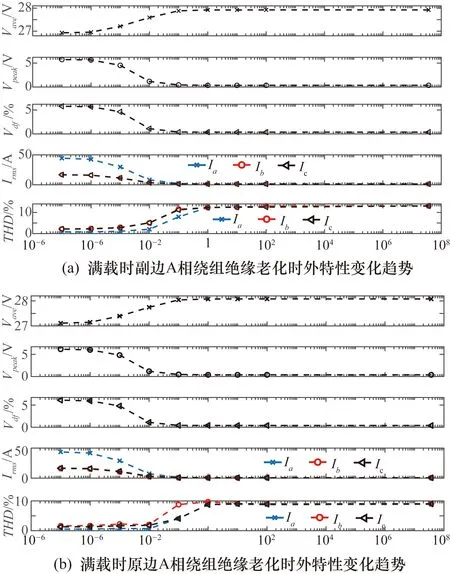
圖4 滿載工況外特性參數隨等效電阻Rpm變化時的趨勢

由圖4外特性變化趨勢可知，可通過輸入電流有效值變化量判斷繞組老化相位。但是在反映變壓器老化狀態時，外特性參數的變化趨勢呈現一定的相關性，外特性參數可能存在冗余變量，如果同時考慮這些參數，將會增加健康管理模型的復雜度和計算量。為了精簡系統老化數據集，需研究測得不同外特征參數間的相關度，以下引入Pearson相關系數。Pearson相關系數能反映變量間線性相關的密切程度，對于變量X、Y之間的Pearson相關系數定義為[8]

(3)

式中：cov(X,Y)為變量的協方差；σx、σy為變量的標準差；E((X-μx)(Y-μy))為求(X-μx)(Y-μy)的數學期望，μx、μy為變量x、y的數學期望，在數值上等于其均值。

樣本變量之間相關程度的量化使用Pearson相關系數corr，其取值范圍為[-1,1]，且相關系數corr的絕對值越大，表明不同因素之間的相關程度越高，計算所有特征和類別標號的相關性，得到參數的相關性并從高到低排列，然后根據需求選取需要的變量作為特征參數集。

以A相電流有效值為基準，其余參數與A相電流有效值相關性的結果如表2所示。從表2可以看出，在繞組絕緣老化時，各參數與A相電流有效值Iarms相關系數大于0.8，說明均與A相電流有效值Iarms呈強相關性。如果考慮全部參數，將會引入冗余變量，增加模型的復雜度和計算量，且通過仿真可知，輸出側電容的狀態不影響三相輸入電流有效值，因此選取A相輸入電流有效值作為表征繞組絕緣老化的特征參數。

表2 不同特征參數與A相電流之間的相關系數

2.2 電容外部特征參數的選擇

根據電解電容的結構特點，可以將其等效為圖5(a)所示的電路[9]。由于電解電容通常使用頻率較低，因此電感Ls的影響可忽略，可將圖中并聯電容電阻等效成串聯形式，得電解電容簡化的等效電路模型如圖5(b)所示。

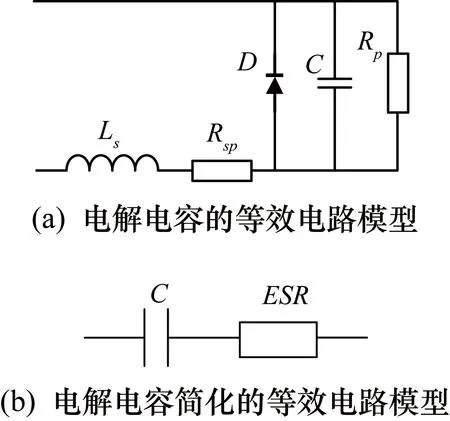
圖5 電解電容的等效電路模型與其簡化模型

一般地，電解液損失40%即能判定電解電容失效，而ESR與電解液存在如下等式的關系：

(4)

式中：ESR0為電容的等效電阻初始值；V0為初始電解液的容量；V為當前電解液容量。于是可得電解電容基于ESR的壽命標準，即當ESR超過初始值的3倍時，電解電容失效。且在電解電容退化的過程中，電容值會隨著電解電容工作時間的增加而減小，其規律近似滿足指數函數的變化規律，且可將電容值減小20%作為電解電容失效的判據。使用LCR測量儀測得多個220 μF電容等效串聯電阻ESR均值為0.25 Ω，所以認為220 μF電容處于完好狀態時電容C為220 μF、等效串聯電阻ESR值為0.25 Ω。

由文獻[9]中設計的電容老化實驗得到的電容量C和等效串聯電阻ESR隨老化時間的變化趨勢可知，隨著老化時間的增加，電容容量C不斷減小，等效電阻ESR不斷增加，兩個參數同時變化,文獻[10]也對鋁電解電容器的失效有所研究。由于電容狀態對輸入側電流無影響，因此只記錄輸出電壓均值Vave、電壓紋波Vpeak和直流畸變系數df。對電容從完好到老化狀態進行仿真，將參數分為表3所示的4個等級。

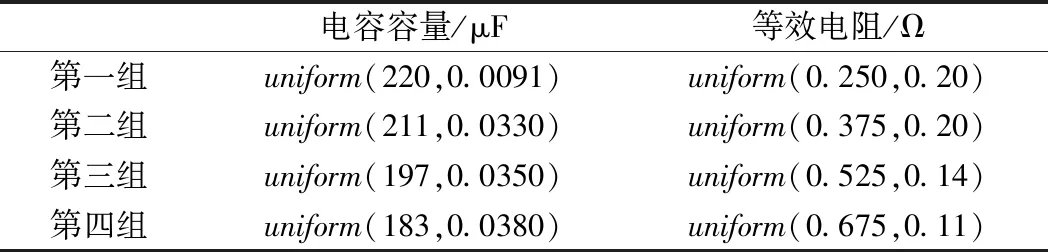
表3 電容容量C和等效串聯電阻ESR不同老化狀態取值范圍

通過仿真表明，隨著電容老化狀態的加劇，電壓均值Vave基本無變化，電壓紋波Vpeak和直流畸變系數df隨電容老化狀態的加劇而增大且趨勢相同，因此選取輸出電壓紋波和直流畸變系數作為表征電容老化的特征參數。

3 系統關鍵器件健康狀態評估算法研究

3.1 健康狀態評估流程

在進行健康狀態評估前,對所用到的方法進行簡單敘述。

高斯混合模型(Gaussian Mixture Model，GMM)是一種常用的基本分布為高斯分布的混合密度模型，它相當于多個高斯概率密度函數的加權平均，每個高斯密度函數被稱為一個分模型，各個分模型的參數相互獨立。高斯混合模型的定義為：設某時刻的觀測值x，它的概率等于該觀測值分別屬于K個高斯分布的概率的加權和，表示為[11]

(5)

(6)

式中:ωk為高斯混合模型中各高斯分布的權重系數；Nk(x|μk,Ck)是均值為μk、協方差矩陣為Ck的第k個多維高斯概率密度函數。

馬氏距離(Mahalanobis Distance)是表示點與一個分布之間的距離。它是一種有效的計算兩個未知樣本集的相似度的方法。對于一個均值為μ，協方差矩陣為Σ的多變量向量，其馬氏距離為

DM=sqrt((x-μ)′Σ∧(-1)(x-μ))

(7)

由于組絕緣老化狀態分為4個狀態，采用4組輸出編碼表示絕緣老化的4個狀態，用數據訓練BP神經網絡netw時，將老化狀態與編碼一一對應，作為神經網絡的目標輸出，對應關系如表4所示，神經網絡參數設置如表5所示。

表4 繞組絕緣狀態對應神經網絡輸出

表5 BP神經網絡netw參數設置

以A相繞組絕緣老化為例，B相和C相繞組絕緣老化評估方法流程相同，由于4種健康狀態邊界點獲取的數據點存在重合點，將不同狀態的數據點直接分類可能存在誤差，使用繞組在健康狀態為“優”、電容健康狀態為“優”時獲取的A相電流有效值用高斯混合模型建立健康基準模型，由“優”狀態數據點高斯混合模型得到的均值與協方差的值，可計算出A相繞組絕緣狀態為“優”、“良”、“中”和“差”時的數據點與健康基準模型的馬氏距離，因此需要根據馬氏距離對原始數據重新分類，再使用重新分類的數據點訓練神經網絡[11-12]。電容老化狀態的評估算法類似，使用電容在健康狀態為“優”、繞組絕緣健康狀態為“優”時獲取的高斯混合模型建立健康基準模型，按同樣流程進行電容的健康狀態評估。

由仿真結果知，電容老化會引起輸出電壓紋波和直流畸變系數增大，而繞組絕緣老化不僅會引起輸入電流有效值增大，也會引起輸出電壓紋波和直流畸變系數增大。因此當繞組絕緣及電容同時老化時，將無法通過輸出電壓紋波和直流畸變系數直接判斷電容的狀態，需要對特征參數進行解耦[13]。

3.2 關鍵部件健康狀態的解耦算法流程

在只考慮繞組發生絕緣老化時，可以通過輸入電流有效值判斷出其老化狀態，在此基礎上再通過輸出電壓均值和輸出電壓直流畸變系數判斷電容老化狀態。因此需要用輸入電流建立繞組絕緣完好時的健康基準模型，以及電容完好時繞組絕緣分別為“優”、“良”、“中”和“差”4組狀態時的健康基準模型。解耦算法的流程如圖6所示。以滿載工況A相繞組絕緣老化為例，先建立繞組絕緣狀態處于“優”、電容處于“優”時的健康基準模型和電容處于“優”、繞組絕緣分別處于4種老化狀態時的4個健康基準模型，由于電容老化狀態對A相輸入電流有效值沒有影響，因此可根據A相輸入電流有效值判斷出繞組絕緣狀態，再進入繞組絕緣處于該狀態且電容處于“優”時的健康基準模型，根據輸出的電壓平均值和直流畸變系數判斷電容健康狀態。

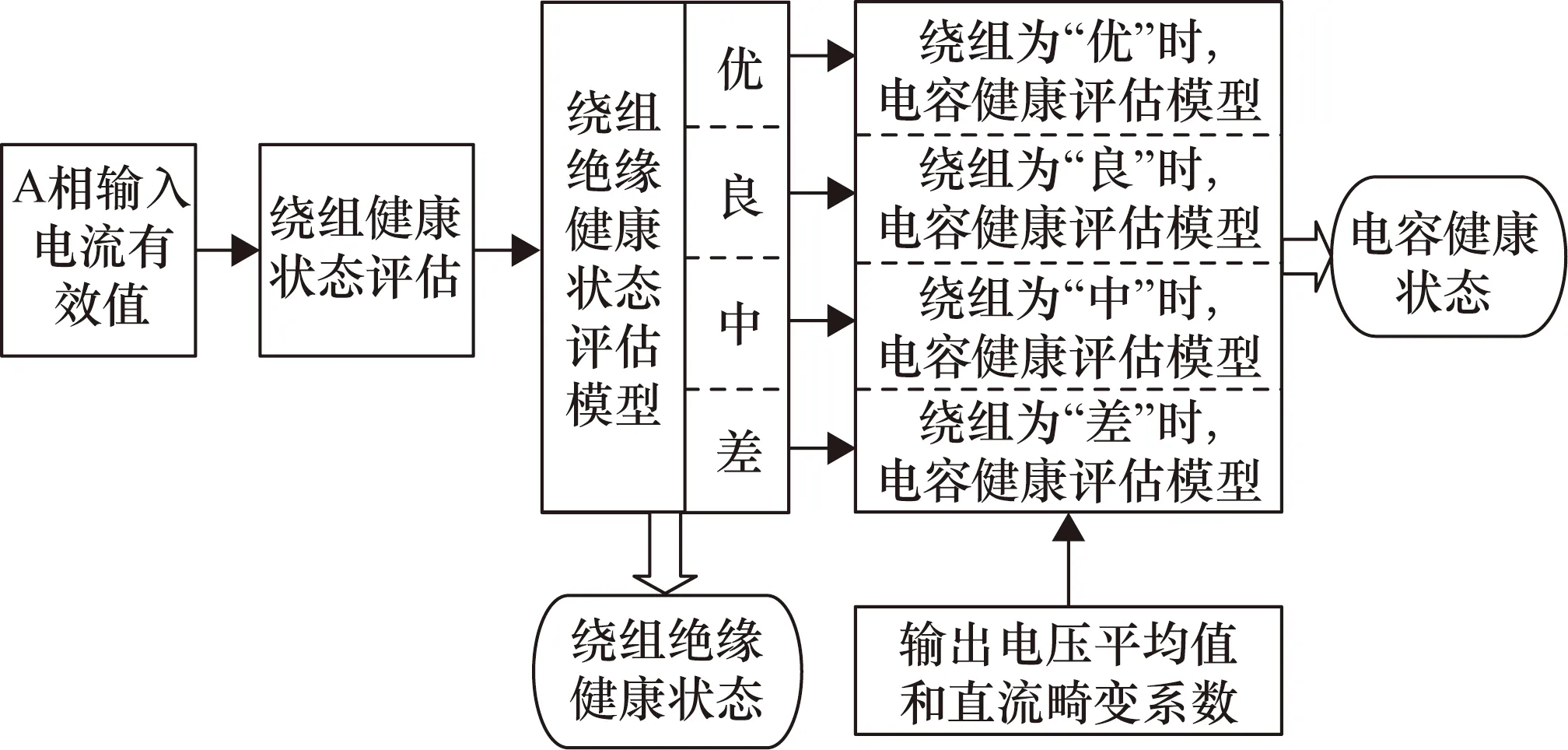
圖6 解耦算法的具體流程圖

3.3 解耦算法實現

在Saber仿真軟件中模擬滿載情況下A相繞組絕緣和電容同時老化，繞組絕緣等效電阻與電容容量和等效串聯電阻處于表6所示范圍，使用蒙特卡羅分析法，每組數據循環仿真100次，獲取繞組絕緣和電容處于不同老化狀態時的外特征參數數據，并在MATLAB中使用第1組數據建立繞組絕緣狀態處于“優”、電容處于“優”時的繞組健康基準模型，用第1、5、9、13組數據建立電容處于“優”，繞組絕緣處于4種老化狀態時電容的4個健康基準模型。

電容處于“優”，絕緣處于不同老化狀態時為第 1、5、9、13 組，將記錄的4組經蒙特卡羅分析法得到的A相電流波形數據導入MATLAB中，通過所編程序計算出400個輸入電流有效值數據點，作為建立高斯混合模型和訓練神經網絡的數據集。電容處于健康狀態“優”、繞組分別處于4個健康狀態時的數據點分布如圖7(a)所示，使用繞組處于健康狀態為“優”時的特征參數建立健康基準模型。由于此時“優”和“良”狀態下的有效值有明顯界限，沒有重疊部分，可直接計算各狀態數據到基準模型的馬氏距離，計算結果如圖7(b)所示，通過計算混疊點的均值作為分類閾值對原始數據重新分類，使用重新分類后的數據點訓練BP神經網絡。

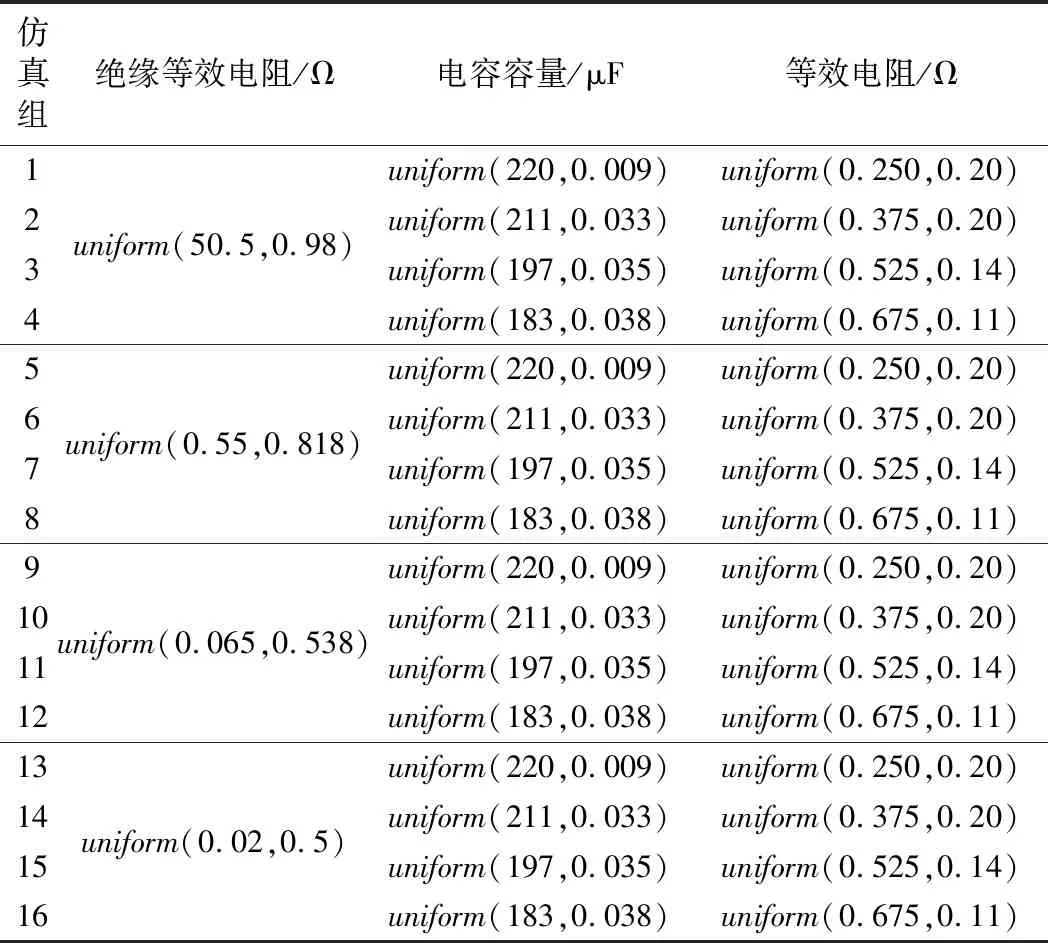
表6 絕緣等效電阻及電容容量和等效串聯電阻取值設置

圖7 電容健康狀態下繞組絕緣不同狀態時特征參數與馬氏距離分布

繞組絕緣健康狀態為“優”，電容分別處于不同狀態時為第1、2、3、4組，將記錄的4組經蒙特卡洛分析法得到的輸出直流電壓波形數據導入MATLAB中，通過所編程序計算輸出電壓均值Vave和直流畸變系數df，作為建立高斯混合模型和訓練神經網絡的數據集，這400個數據點的分布如圖8(a)所示，使用繞組處于健康狀態時的特征參數建立電容的健康基準模型。計算出“優”健康狀態下歸一化后大于0的數據點與另外3種老化狀態下各數據點到基準模型的馬氏距離如圖8(b)所示，并通過計算混合點的均值作為分類閾值對原始數據重新分類，使用重新分類后的數據點訓練BP神經網絡。繞組絕緣健康狀態為“良”時，對電容健康狀態評估為“優”的方法類似。

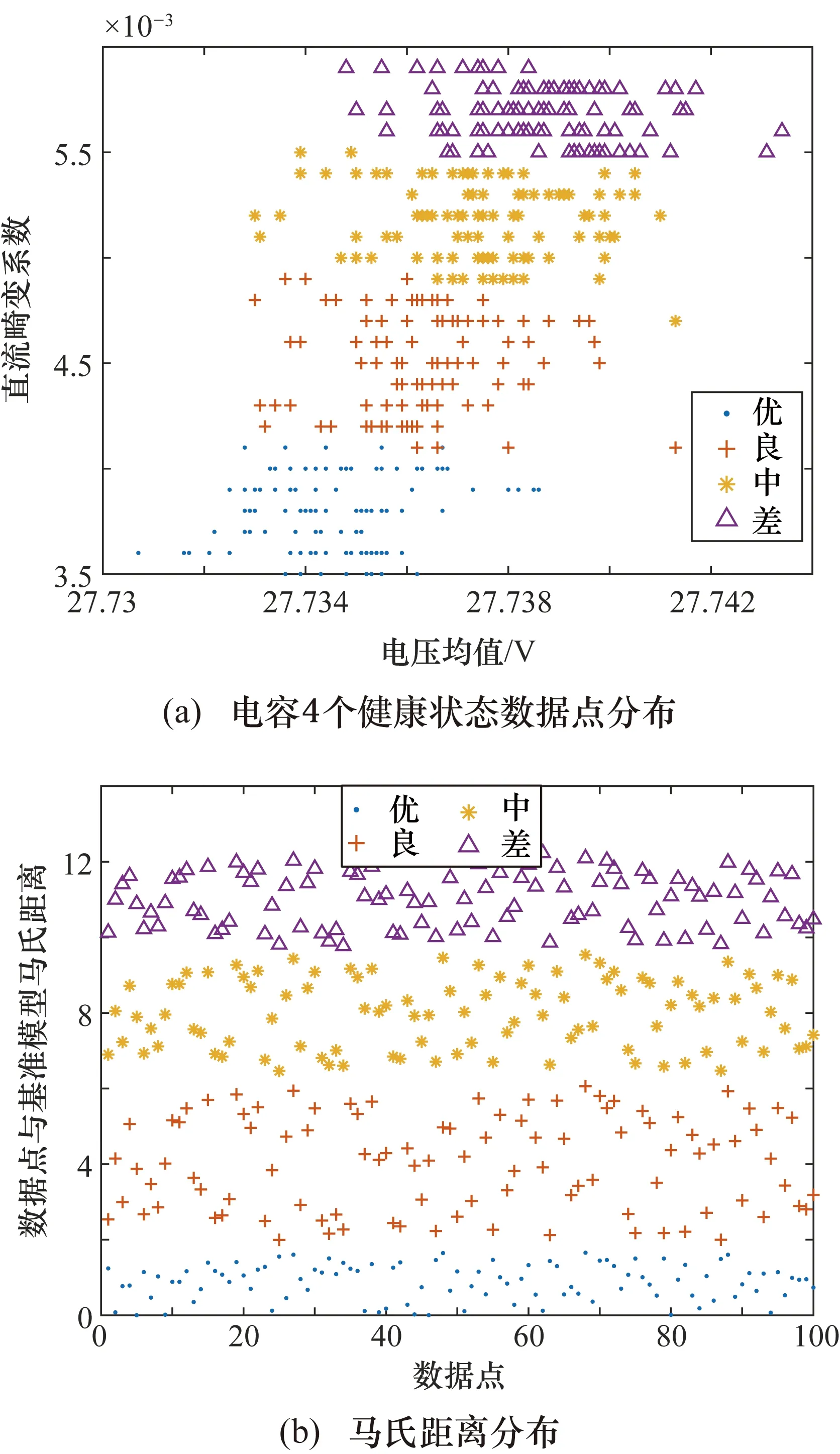
圖8 繞組絕緣健康狀態下電容不同狀態時特征參數與馬氏距離分布

繞組絕緣處于健康狀態為“中”，電容分別處于4個健康狀態時的仿真組為第9、10、11、12組，仿真得到的400個數據點分布如圖9(a)所示。由于此時絕緣繞組的健康狀態對輸出特性的影響作用加重，數據點呈長條狀分布，4組老化狀態數據點到基準模型的馬氏距離甚至可能小于處于“優”健康狀態數據長條兩端的數據點到基準模型的馬氏距離，且通過直流畸變系數區分數據點會出現混合現象，如圖9(b)所示，此時根據上述的馬氏距離分類方法不能準確辨別電容的狀態，故選擇通過原始數據中電壓均值Vave和直流畸變系數df的對應關系來對電容狀態進行判斷，計算出“優”健康狀態下的數據點與另外3種老化狀態下各數據點到基準模型的馬氏距離，如圖9(c)所示，通過計算混合點的均值作為分類閾值對原始數據重新分類，使用重新分類后的數據點訓練BP神經網絡。繞組絕緣健康狀態為“差”時，仿真數據點分布與繞組絕緣健康狀態為“中”的方法類似。

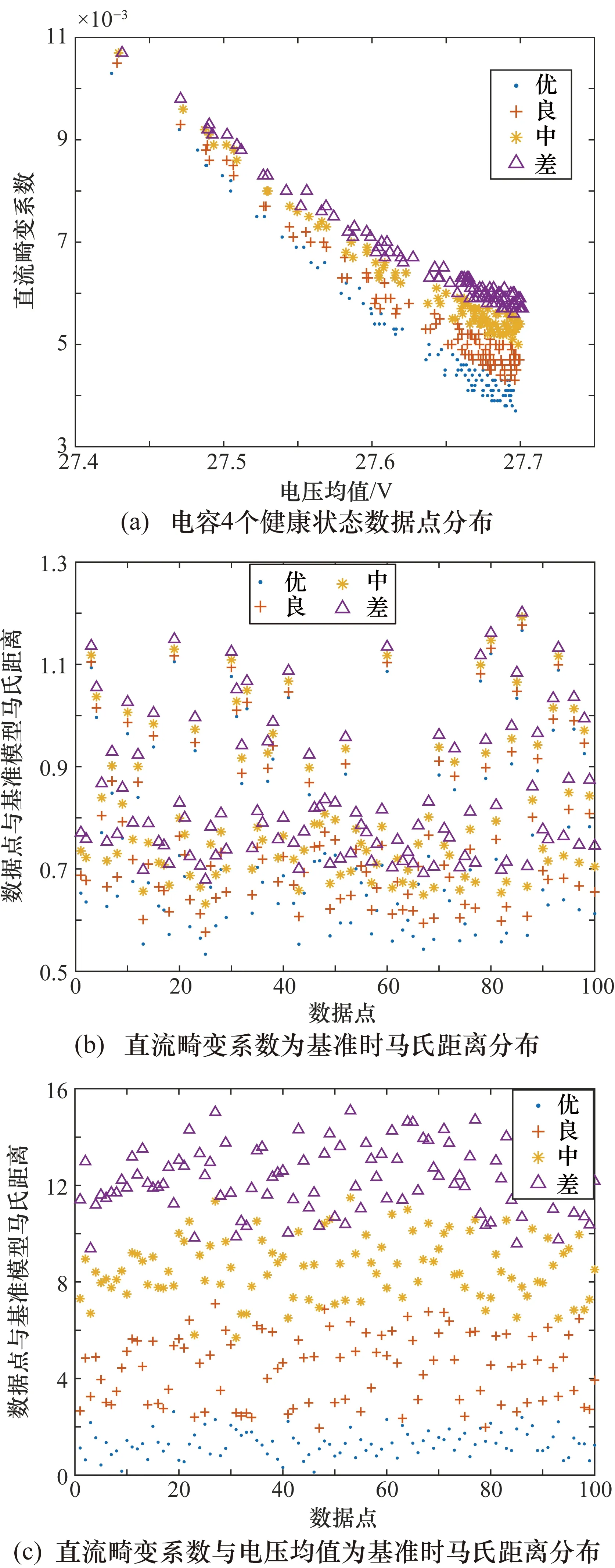
圖9 繞組絕緣“中”狀態下電容不同狀態時特征參數與馬氏距離分布

3.4 解耦算法驗證

為了驗證該解耦算法對變壓整流器系統健康狀態評估的準確性，在滿載工況下，分別在Saber中對繞組絕緣等效電阻、電容容量和等效串聯電阻按照表4中的16組范圍賦值，每組數據進行25次蒙特卡羅分析，記錄每組由蒙特卡羅分析法所獲得的A相電流有效值、輸出電壓均值和直流畸變系數，將16組仿真組分為4組測試集分別驗證對繞組絕緣以及電容老化狀態的判斷，將神經網絡期望輸出結果與實際輸出結果進行對比，驗證結果如表7所示，可以看出該神經網絡對各健康狀態數據點判斷的準確性均在90%以上，符合預期目標，因此該解耦算法可用于變壓整流器的健康狀態評估。

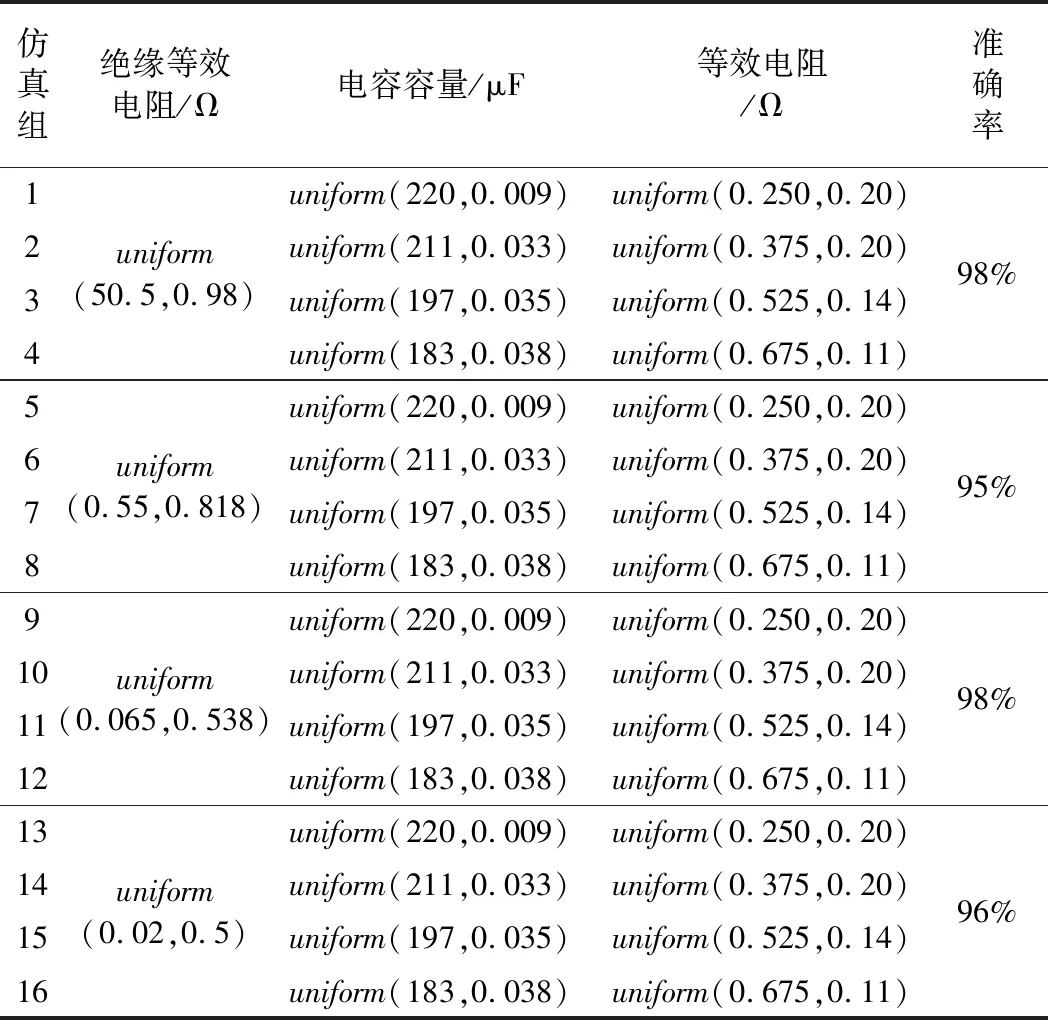
表7 測試數據的期望輸出與神經網絡輸出對比

系統整體健康狀態評估流程如圖10所示，首先通過導入的輸出電流均值判斷出系統的工況：計算三相輸入電流有效值與此工況下絕緣完全健康時所測三相輸入電流有效值差值，即將ΔIarms、ΔIbrms、ΔIcrms3個值進行比較，電流差值最大相為發生絕緣老化的相位；然后使用對應工況和發生繞組絕緣老化的相下建立的健康狀態評估算法模型進行評估。如圖10中判斷出繞組絕緣老化狀態為滿載A相繞組絕緣老化，使用在滿載A相絕緣老化時的健康基準模型進行判斷，根據輸入的A相電流有效值Iarms可以判斷出繞組絕緣的健康狀態，然后通過輸出電壓直流畸變系df和輸出電壓均值Vave，由該繞組絕緣狀態下電容的健康狀態評估模型判斷出電容的健康狀態，完成變壓整流器系統健康狀態評估，其他工況和繞組絕緣老化時的健康狀態評估流程與上述相同。

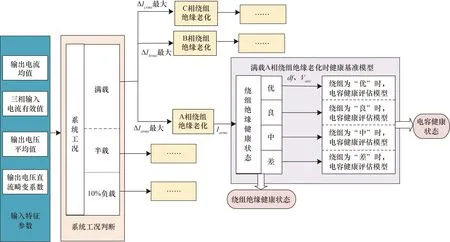
圖10 系統整體健康狀態評估流程圖

4 結束語

本文以航空變壓整流器為對象，研究其健康狀態評估算法，實現飛機變壓整流器系統健康狀態的評估。首先分析了變壓整流器的結構和工作機理，對變壓整流器的老化關鍵部件進行選取，通過Saber軟件進行蒙特卡羅分析獲取不同老化狀態的變壓整流器輸出特性，提取能夠表征變壓整流器健康狀態的外特征參數,根據提取的外特征參數，分別建立繞組和電容的健康基準模型，并根據各狀態的數據點與健康基準模型的馬氏距離對原始數據進行分類，然后使用分類后的數據訓練BP神經網絡，用于系統的健康狀態評估。

此外，針對繞組絕緣和電容同時老化的情況，給出了采取解耦算法的流程：首先通過輸入電流判斷出繞組健康狀態，再根據繞組處于該狀態時的電容健康基準模型，使用健康狀態評估算法評估電容的健康狀態。同時，本文僅考慮了不同工況時，繞組絕緣和電容的健康狀態評估，未考慮三相不平衡時的情況，同時本文中變壓整流器的數據獲取是通過仿真獲得，與實際數據有一定差別，希望今后可以獲得飛機變壓整流器實際數據，從而提高健康狀態評估算法的準確性。