基于三力匯交原理分析均質桿的平衡問題

慎晨樂 沈 衛

(湖州市菱湖中學 浙江 湖州 313018)

在高中階段對于均質直桿的受力平衡問題往往采用力矩平衡結合共點力平衡的關系進行定量解析.但是考慮到高中階段大多數的同學并不熟悉力矩平衡的概念及其規律，因此,在解決桿平衡的問題時不妨采用共點力平衡下的三力匯交原理來進行分析.如果均質直桿受到3個非平行力的作用而處于平衡狀態，則這3個力必為共點力[1]，力的延長線必然相交于同一點.因此,對于兩端受力的均質直桿而言，當3個力匯交于同一點后，可以對力所構成的平行四邊形進行幾何關系的定量分析.

1 共點力作用下分析直桿受力的幾何方法呈現

當均質直桿兩端受到互不平行力的作用而處于平衡狀態時，依據三力匯交原理可以構建力的平行四邊形.若平行四邊形中存在直角三角形，則可從三角函數的關系著手列方程；若平行四邊形中無直角三角形，則可從正弦定理著手列方程；當直桿的兩端存在未知大小的力時(如桿的一端與鉸鏈連接或者與粗糙地面接觸等)，可以依據相似三角形邊長的相似比相等列方程求解. 下面通過一個具體的問題實例來加以探討.

【例1】如圖1所示，質量分布均勻的直桿AB置于水平地面上，現在A端施加外力F，緩慢抬起直桿至豎直，B端始終和地面保持相對靜止，F的方向始終和直桿垂直，要確保直桿B端始終和地面保持相對靜止，則直桿和地面間的動摩擦因數至少為多少？

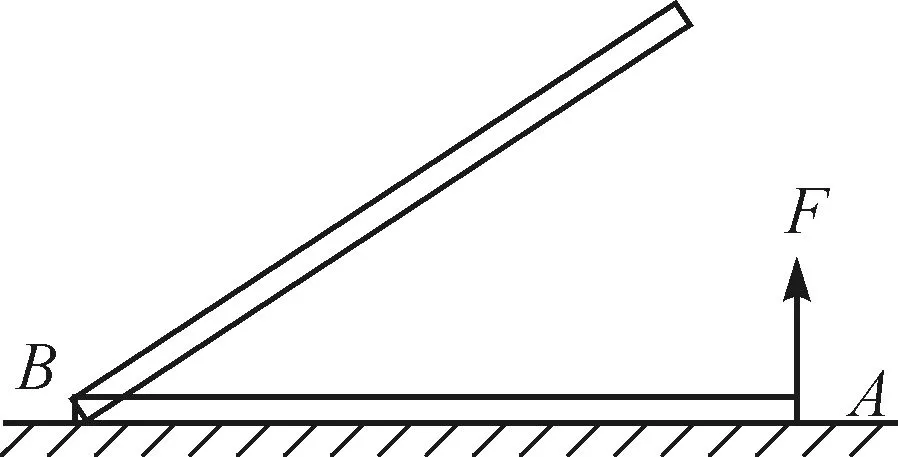
圖1 外力F作用下的直桿AB

1.1 運用正弦定理列方程求解

直桿AB被緩慢地提起且B端靜止不動，顯然處于動態平衡狀態，對其受力分析發現受重力mg和外力F以及地面的支持力與摩擦力(可合成為一個力F′)，且這些力的方向并不平行，因此力的延長線必然匯交于同一點，故可作受力分析圖如圖2所示.

圖2 直桿AB的受力分析圖

根據圖2，若B端始終與地面保持相對靜止，則角α不能大于B端的摩擦角，即角α的正切值滿足：tanα≤μ.

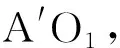
根據正弦定理，在△OCO1存在

(1)

其中OO1邊和OC邊的邊長滿足

(2)

聯立表達式(1)、(2)，消去L可得

cosθsin(α+θ)=2sinα

對該式進行整理可將之轉化為關于tanα的表達式

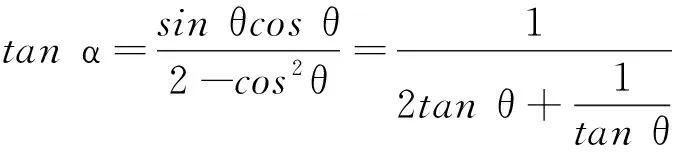
1.2 從相似三角形相似比的角度構建力的關系

既然△OCO1與直桿平衡狀態下三力所構成的閉合三角形為相似三角形，則由邊長的相似比可知

(3)

根據圖2，在△A′BO1中存在

(4)

聯立表達式(3)、(4)可得

因此，地面對直桿B端的支持力FN與摩擦力f滿足

即

同樣可得到動摩擦因數應滿足的最小值.

可見要解決均質直桿在共點力作用下的平衡問題，如果要避開對力矩平衡關系的應用，則要充分滲透對三角形幾何關系的運用.不僅要依靠正弦定理把握非直角三角形3力之間的定量關系，還要根據邊角的相似特征(如桿的長度、桿與水平面的夾角等)找尋相似三角形，依據相似比建立方程，實現對力大小與方向的解析.

2 基于相似三角形關系深化方法的運用

利用三力匯交原理構建力矢量三角形的相似三角形，將對力大小的求解依托于相似三角形相似比的討論中，并依據重力已知的條件，實現對直桿兩端受力大小的求解.下面再通過一個問題的求解進一步對該方法的運用進行展示與深化.

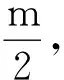
圖3 機場候機樓的結構簡圖

分析：由對稱性可對一側的斜壁進行受力分析，其受力分析圖如圖4所示;將鋼索與屋面看成整體，其受力分析圖如圖5所示.

圖4 斜壁的受力分析圖

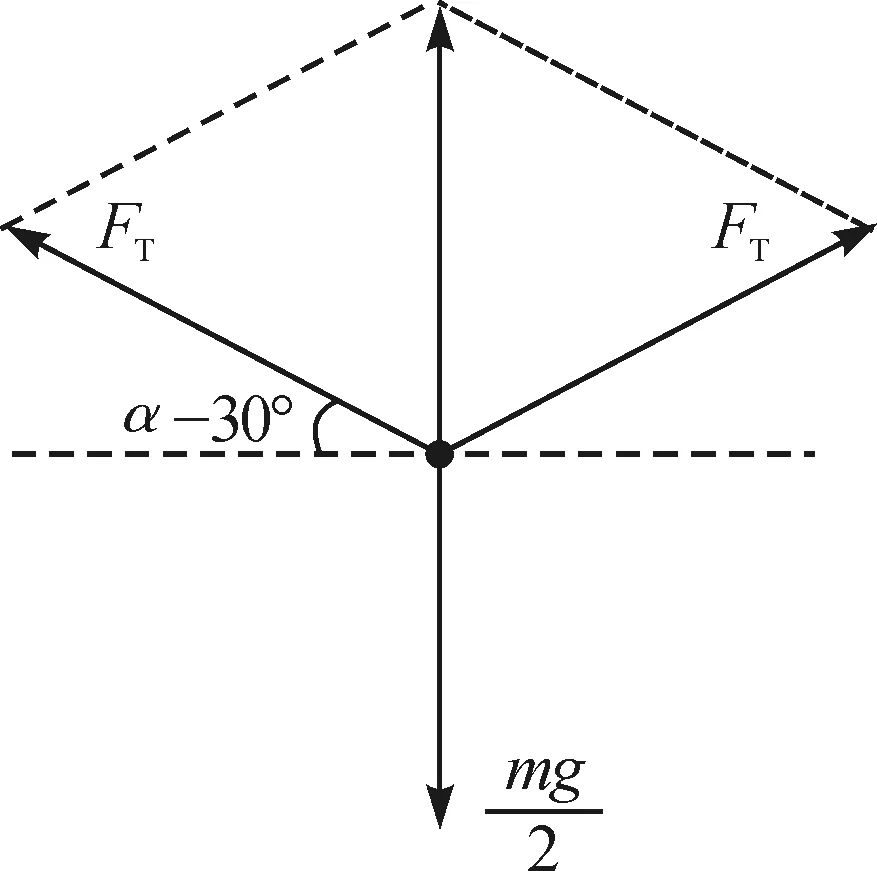
圖5 鋼索與屋面整體的受力分析圖

取斜壁與地面的夾角為α，由圖5可知斜壁對鋼索的拉力FT滿足

(5)

由圖4中力的平行四邊形定則可知，存在力的矢量三角形與△ACO1為相似三角形，因此,根據邊長與力的相似比關系，可構建拉力FT與斜壁重力mg之間的關系為

(6)

取斜壁AB的長度為L，由邊角的幾何關系可知O1C邊與CA邊的邊長滿足

|CA|=Lsinα-Lcosαtan(α-30°)

(7)

聯立表達式(5)～(7)并消去表達式中的L與mg整理得

3tan(α-30°)=tanα

由此可知斜壁與地面的夾角α=60°，斜壁對鋼索的拉力為

依據三力匯交原理分析均質直桿的受力平衡問題所關聯的還是高中階段共點力平衡的力學知識，只是在問題解決中對知識與方法的運用有更高的要求，主要體現在：

(1)只有清晰、規范地展現物體的受力情況，才能從中發掘共性、形成關聯，構建出問題解決所需要的等式與方程.因此,要引導同學們正確認識受力分析在解決力學問題中的功能與作用，使同學們明白受力分析不僅要會畫受力分析圖，還要畫好受力分析圖(包括作圖習慣的養成、作圖規范的生成、作圖工具的運用等).

(2)對三角幾何知識的運用有更高的要求，不僅體現在使同學們能夠處理與直角三角形有關的力平衡問題，更多的情況下是對非直角三角形平衡關系的定量分析.這就需要同學們在平時的學習中注重學科間知識的遷移與結合，拓寬方法運用的“臨界點”，使中學數學知識更好地、更有效地用于對物理問題的分析與解決.