基于數據挖掘技術的網絡控制系統建模與分析

劉 明

(河北工業大學 廊坊分校， 河北 廊坊 065000)

網絡控制在控制領域中占有重要地位，網絡控制系統是利用通信網絡建立環路的系統[1].網絡控制系統通常包括控制器、執行器以及傳感器三部分，是典型的閉環反饋控制系統.網絡控制系統由于引入網絡，容易造成數據傳輸誘導時延情況[2].誘導時延存在于網絡中將影響系統穩定性，設計網絡控制系統時，需充分考慮網絡誘導時延情況，提升控制系統可靠性.

目前針對系統控制研究較多，趙晉泉等[3-4]將模型預測控制方法應用于異采樣率雙環網絡控制系統中；王蘭等[5]利用準ARX多層學習網絡模型自適應控制非線性系統，可實現系統控制，但由于未采用數據挖掘方法確定控制參數，影響其控制性能.數據挖掘方法是搜尋海量數據中所存在隱含規律的重要方法，分析海量數據將其中所包含有用知識提取[6]，數據挖掘方法已廣泛應用于行為預測以及建模中.以往數據挖掘方法未考慮包含時間信息的動態數據，僅考慮靜態時間數據.網絡控制系統運行過程中持續采樣[7]，存在海量差異時間序列數據，需采用動態數據挖掘方法挖掘系統中相關數據.因此，本文提出基于數據挖掘技術的網絡控制系統建模與控制方法，建立網絡控制系統數學模型，利用動態數據挖掘方法挖掘網絡控制系統中海量時間序列數據中隱含規律，基于所挖掘規律確定網絡控制系統控制參數，制定控制決策，提升網絡控制系統的性能.

1 網絡控制系統建模與控制方法

1.1 網絡控制系統建模

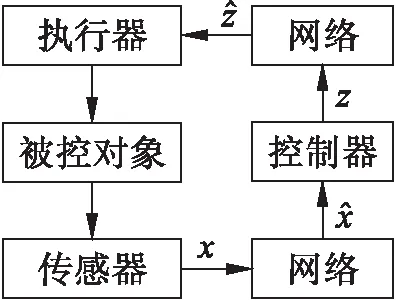
圖1 網絡控制系統總體結構圖Fig.1 Overall structure diagram of network control system

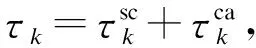
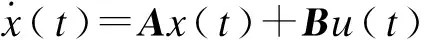
(1)

式中：x(t)∈Rn與u(t)∈R分別為待控制對象狀態以及輸入；A、B為適維矩陣.

網絡存在誘導時延的信號時序公式為

(2)

利用離散數學模型表示網絡廣義對象為

xk+1=Gxk+Γ0(k)u(k)+Γ1(k)u(k-1)

(3)

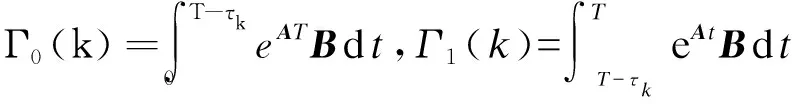
(4)

可將式(3)轉化為

xk+1=Gxk+Huk-1+Γ0(k)Δu(k)

(5)

式中：Δu(k)為時延滯后；uk-1為網絡帶寬限制.將矩陣A轉化為

(6)

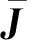
設僅存在一個0特征值以及r重特征值于矩陣A中，可將A轉化為

A=Λdiag(0，J1，J2)Λ-1

(7)

式中，J1與J2分別為對角塊以及若爾當塊.可將Γ0(k)轉化為

(8)

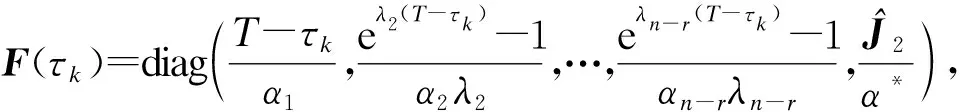
Γ0(k)=DF(τk)E

(9)

式中，D、E為定常矩陣.可得離散化表示廣義被控對象的網絡控制系統數學模型為

xk+1=Gxk+Huk-1+DFEΔuk

(10)

1.2 動態數據挖掘

1.2.1 樣本抽取

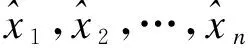
(11)

Yk=[y1(t0+kΔT)，y2(t0+kΔT)，

…，ym(t0+kΔT)]T

(12)

式中，t0為初始采樣時刻.

1.2.2 特征模式評價

確定待挖掘樣本后，利用時間序列挖掘網絡控制參數過程如下：

1) 用Si={sil，…，sij，…，siq}表示控制參數測量值時間序列模式指標集合，其中，sij表示測量值xi時間序列的第j種控制參數指標.

(13)

式中，fsij為分形維數評價算法.

通過特征模式評價過程，利用模式評價值序列表示時間序列數據[12]，其中不包含時間因素.

1.2.3 數據挖掘

動態數據挖掘主要包括樣本抽取、依據所設定特征模式控制參數針對時間序列實現特征模式評價，以及依據控制要求設定關聯模型三部分，具體過程如下：

1) 確定網絡控制系統控制參數.

2) 依據可能影響網絡控制參數的因素確定控制參數相應特征模式評價指標集合以及數量為n的控制參數.

3) 獲取網絡控制系統傳感器測量值時間序列[13]，抽取時間序列獲取數據挖掘樣本.

4) 將數據樣本利用模式評價方法轉化為模式評價樣本.

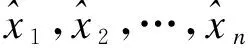
Y(τ)=f(X(τ)，X(τ-Δt)，X(τ-2Δt)，

…，X(τ-NΔt))

(14)

式中：X=[x1，x2，…，xn]T與Y=[y1，y2，…，ym]T分別為測量值向量以及控制參數向量；N為測量值時間序列長度.

6) 對挖掘結果選取測試樣本集進行測試.

7) 將數據挖掘結果輸出，確定網絡控制系統最佳控制參數.

1.3 系統控制方法

利用分數階PIλDμ控制器對非線性和時變參數的控制優勢，分別對微分項階次μ以及積分項階次λ進行控制.以上兩參數均為隨機實數，通過兩參數改善傳統PID控制器無法實現時變環節以及產生非線性環節跟蹤的劣勢.時域表達分數階控制器公式為

u(t)=KPe(t)+KID-λe(t)+KDDμe(t)

(15)

式中：KP與KI分別為分數階控制器的比例增益與積分增益；KD為微分增益；積分項階次λ以及微分項階次μ均大于0.

分析以上過程可知，采用無限維的濾波器表示分數階控制器[15]，依據閉環特征方程性能指標與零極點令微積分階次以及控制參數有所優化.獲取分數階控制器傳遞函數表達式為

G(s)=KP+KIs-λ+KDsμ

(16)

可得利用分數階控制器控制網絡系統結構圖如圖2所示.圖2中，R(s)與E(s)=R(s)-Y(s)分別表示系統輸入以及輸出；U(s)與Y(s)分別表示控制器輸入以及輸出.

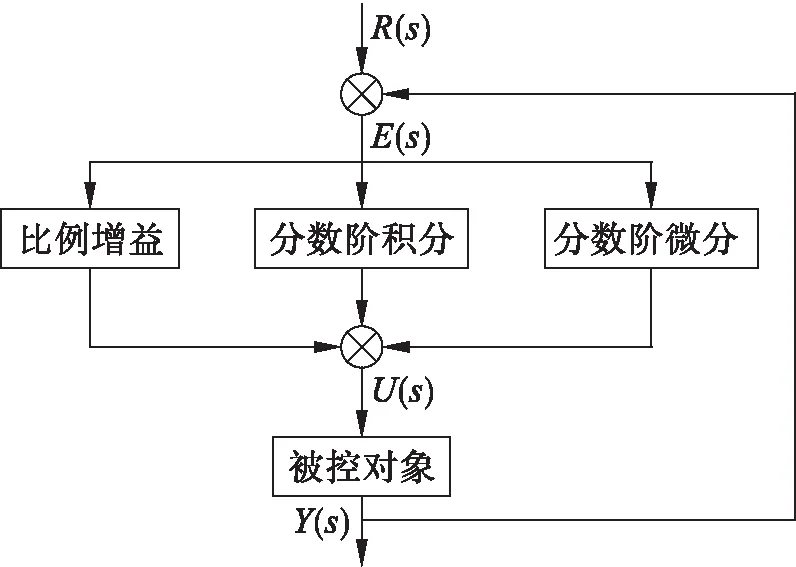
圖2 分數階控制器結構圖Fig.2 Structure diagram of fractional order controller

2 實例分析

為驗證采用本文方法建立網絡控制系統數學模型的有效性，采用Matlab軟件搭建所建立網絡控制系統數學模型.設定網絡總體時延呈現正弦變化，峰值為0.02 s，網絡時延頻率為0.1～10 Hz.采用的PIλDμ控制器輸入信號為方波信號，傳感器采樣周期為0.01 s，微分增益為100 000，微分系數為0.05.選取ARX方法(參考文獻[5])以及模型預測方法(參考文獻[6])作為對比方法.

統計采用三種方法控制網絡控制系統，即無時延、短時延以及長時延情況下系統的狀態響應曲線，利用所獲取狀態響應曲線驗證不同方法的控制效果.狀態響應曲線對比結果如圖3所示.由圖3對比結果可以看出，相同網絡環境下，采用本文方法控制的網絡控制系統穩定速度較快，說明本文方法可良好控制網絡控制系統.本文方法采用分數階控制器調節系統狀態，具有明顯的約束效應，所獲取控制效果明顯.無時延、短時延以及長時延情況下，本文方法均具有最優的狀態響應性能，可有效補償網絡控制系統的網絡時延.采用三種方法控制網絡控制系統的超調量均隨著時延增大而有所增大，說明系統時延增加影響系統運行的動態性能.本文方法在不同時延情況下均具有較高的反應速度，控制性能優越.

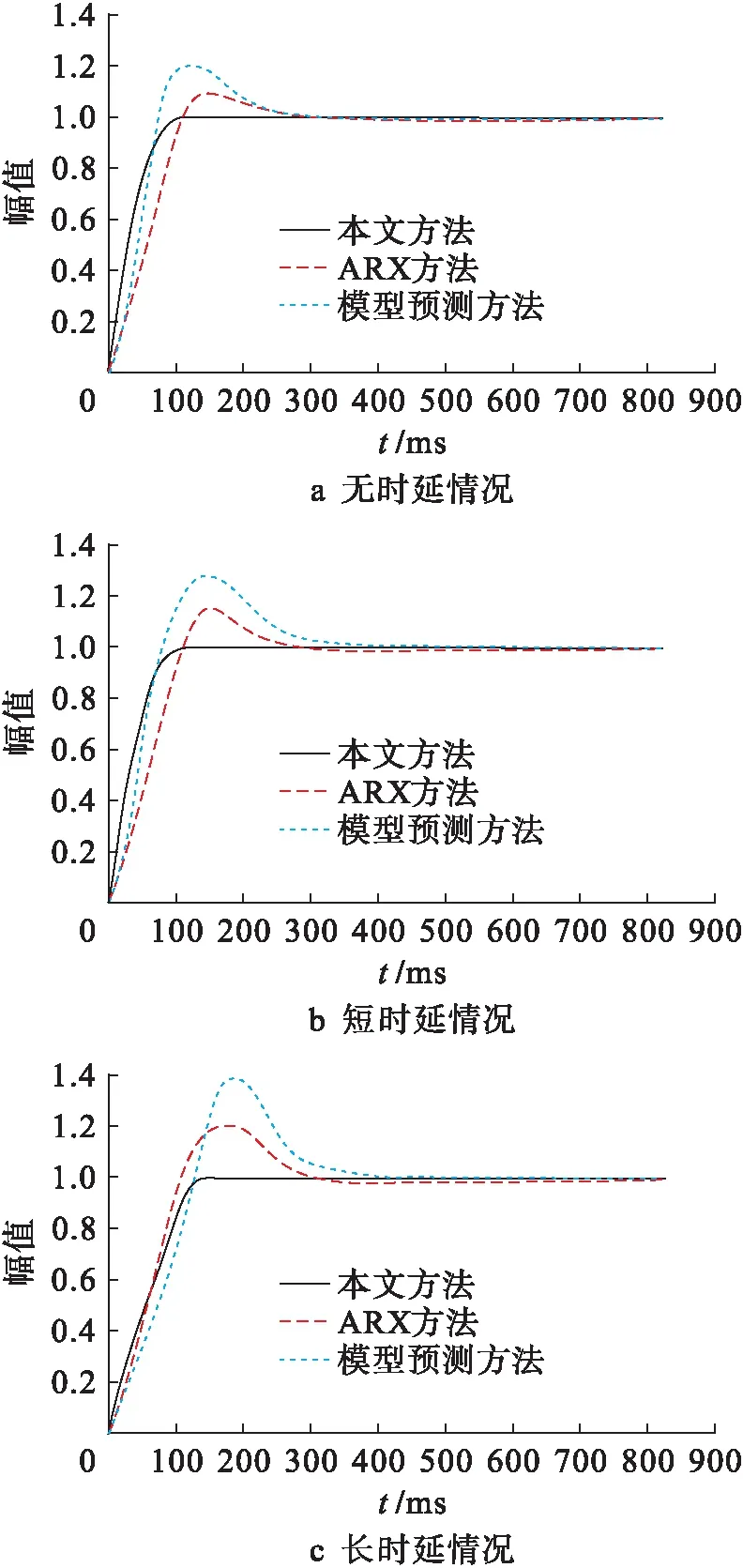
圖3 狀態響應曲線Fig.3 State response curves

網絡控制系統中的執行器、控制器以及傳感器利用網絡實現通信，容易出現連接中斷以及信息碰撞等情況，導致傳輸信息過程中出現時延，網絡時延主要由數據分析、處理和傳輸造成.采用三種方法控制網絡控制系統，系統運行800 ms以內時延分布對比結果如圖4所示.由圖4時延對比結果可以看出，網絡控制系統運行不同時間內，采用本文方法控制系統的時延明顯低于另兩種方法，說明采用本文方法控制網絡控制系統可有效改善網絡控制系統的時延情況，提升系統響應速度.

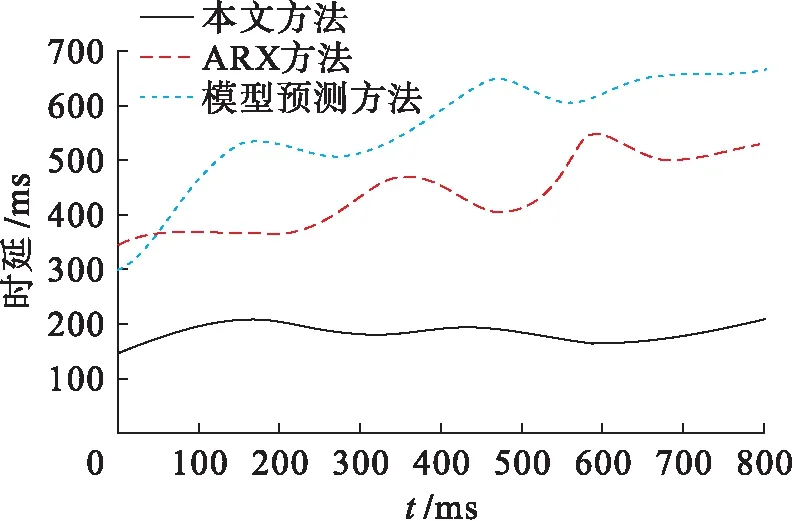
圖4 時延分布對比Fig.4 Comparison of time delay distribution

網絡控制系統數據傳輸方式主要包括單包傳輸以及多包傳輸.丟包率可有效體現系統受不同情況干擾的控制性能.針對不同傳輸方式，采用三種方法控制網絡控制系統，系統運行800 s以內丟包率對比結果如圖5所示.網絡控制系統通信過程中出現數據包丟失的主要原因是信道干擾、通信故障以及通信沖突頻繁.網絡負荷越大，系統丟包率越高.由圖5對比結果可以看出，采用本文方法控制網絡控制系統，不同運行時間內系統丟包率均為最低.采用本文方法控制網絡控制系統，單包傳輸以及多包傳輸情況下丟包率均低于0.2%.對比結果表明，采用本文方法控制網絡控制系統，可使系統具有較高的傳輸性能.

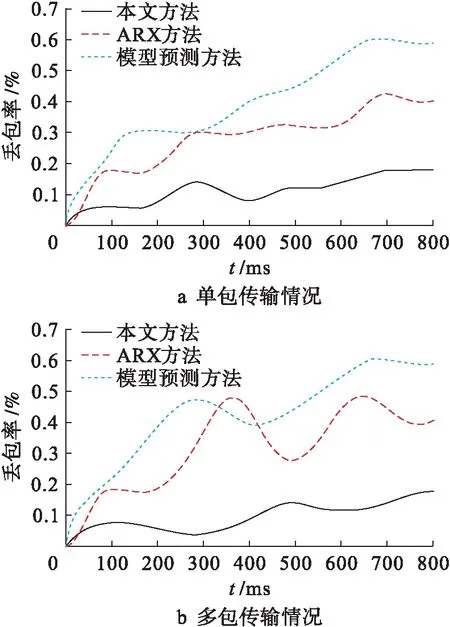
圖5 丟包率對比Fig.5 Comparison of packet loss rate

在確定網絡控制參數時，是以傳感器的測量值時間序列以及控制參數時間序列為基礎，對海量數據進行空間和時間相關聯的挖掘，并抽取子序列，據此進行網絡傳輸時動態數據的挖掘.在此過程中，由于控制了傳輸周期內信號的挖掘優先性，在去除無關序列的數據時，最大程度地保存了有效數據，實現了較全面的數據傳輸，降低了丟包率.

3 結 論

將數據挖掘技術應用于網絡控制系統中，充分考慮網絡傳輸時延對系統運行的影響，建立網絡控制系統數學模型.利用數據挖掘方法挖掘系統中海量信息所包含的隱含規律，明確控制參數，利用分數階PID控制器實現網絡控制系統的良好控制.通過實驗驗證所研究控制方法具有較好的控制有效性，不同傳輸方式時仍具有極高的控制效果.