大跨越輸電塔四鋼管組合柱穩定承載力研究

甘懿德 鄧洪洲 李秉澤

（同濟大學建筑工程系，上海 200092）

0 引 言

為了滿足經濟發展帶來的日益增長的用電需求，新建輸電線路電壓等級越來越高，輸電鐵塔日趨大型化，其荷載也相應增大。蘇通長江大跨越工程中擬建的兩座跨越塔，設計塔高455 m，檔距2 600 m，塔腳處主材軸力設計值達到2.5×105kN。如果仍然采用傳統的單鋼管混凝土主柱，主柱最大截面將達到Φ2 750 mm×44 mm，不僅難以加工、運輸和施工，還伴隨著截面過大帶來的局部穩定問題和過厚鋼材層狀撕裂問題。因此，該大跨越工程設計階段提出了如圖1所示的四管組合柱方案，即在變坡節點以下采用由四根較小直徑主管通過鋼連梁連接形成的四管組合柱來作為輸電塔的主要受力構件。

輸電塔四鋼管組合柱主要承受軸壓力，采用連梁連接，受力接近綴板柱。而由于輸電塔工程自身特點限制，組合柱長細比、分肢間距小，綴板分肢線剛度比不能滿足現有規范中綴板柱計算公式的要求。因此對于四管組合柱這種新式的輸電塔主柱，如何計算穩定承載力以及確定合理的連梁線剛度成為其應用過程中的需要解決的主要問題。

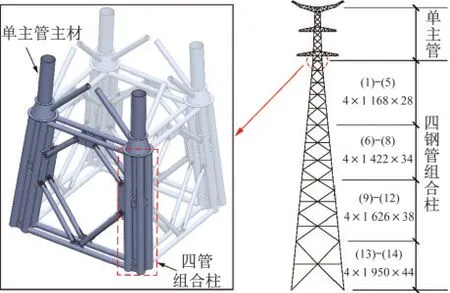
圖1 蘇通大跨越四鋼管組合柱輸電塔（單位：mm）Fig.1 Sutong large-span transmission tower（Unit：mm）

組合構件穩定承載力研究較為成熟。Engesser最早提出了考慮剪切變形影響的實腹柱彈性屈曲荷載公式；Timshenko[1]通過假定反彎點在綴板和分肢中心將該方法引入組合柱穩定計算中，目前對于多種形式格構柱的穩定承載力研究均采用此種方法[2-4]。此外，一些學者還提出了不同于Engesser法的組合構件計算方法，如Tong等[5]提出的格構柱修正夾層梁理論、Gjelsvik[6]給出的組合柱的六階控制方程、A.G.Razdolsky[7]采用的組合柱整體分析法。

組合柱目前主要有兩種設計方法。一種是《鋼結構設計標準》（GB 50017—2017）[8]所采用的換算長細比法，另一種是歐洲鋼結構規范[9]采用的單肢驗算法。換算長細比方法通過組合柱換算長細比查閱穩定系數，從而計算彈塑性穩定承載力。該方法的優勢是簡單直觀，缺點是假設了組合柱初始缺陷與實腹柱相同，不能考慮組合柱分肢受力不均的影響。而單肢驗算法則能考慮此種缺陷的影響。

本文根據輸電塔四管組合柱特點，首先在考慮初彎曲的單肢驗算法基礎上推導了考慮初彎曲和初偏心的單肢驗算法公式；其次以有限元彈性屈曲分析為依據研究了不同換算長細比公式的適用性，并結合組合柱彈塑性屈曲有限元分析研究了基于不同換算長細比公式的換算長細比法和單肢驗算法公式的適用性；最后以蘇通大跨越輸電塔為案例，對組合柱彈塑性穩定承載力計算方法進行驗證。

1 四管組合柱計算方法

1.1 Engesser法

1.2 單肢驗算法

單肢驗算法是計算組合柱彈塑性穩定承載力的主要方法之一。考慮到輸電塔四管組合柱長細比較小，初偏心對穩定承載力影響較大，四管組合柱繞45°對管方向彎曲時對分肢主管受力最為不利，因此在計算模型中假設四管組合柱在45°對管方向有等效初彎曲和端部初始偏心e，如圖2所示。

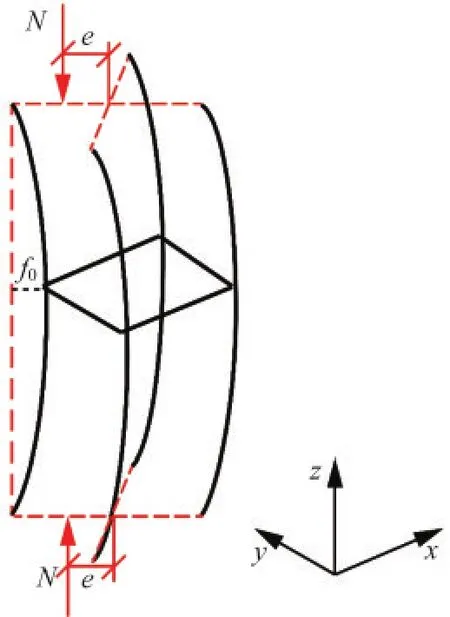
圖2 分析模型Fig.2 Analysis model

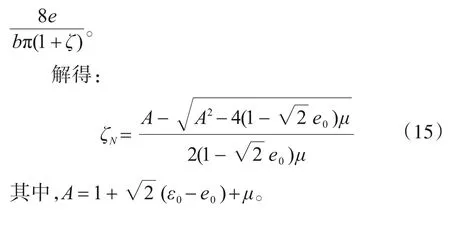
2 有限元分析

在輸電塔四鋼管組合柱參數范圍下，結合有限元分析對僅考慮綴板和分肢彎曲的換算長細比公式[式（4）]、考慮綴板和分肢彎曲及綴板剪切的換算長細比公式[式（3）]以及計算彈塑性穩定承載力的換算長細比法和單肢驗算法進行對比驗證，并通過有限元分析線剛度比對輸電塔組合柱彈塑性屈曲荷載的影響。

輸電塔四鋼管組合柱分析參數規定如下。分肢主管截面取為Φ800 mm×20 mm，分肢凈間距取400～800 mm以滿足最小施工間距要求并保證組合柱整體性。組合柱線剛度比范圍為1≤k≤6，名義長細比范圍10≤λ≤160。為了避免分肢失穩，分肢長細比均滿足GB 50017—2017的要求。分肢主管和工字連梁的材料分別為Q420、Q345鋼。計算模型中，為了便于對組合柱作規律性分析，柱端約束假定為鉸接。由于實際輸電塔鋼管柱長細比小，柱端約束有一定剛度，為了考慮端部彎矩的影響，在彈塑性屈曲分析時同時設置了初彎曲和初偏心兩種缺陷。

本研究采用ANSYS開展輸電塔組合柱有限元分析。有限元模型如圖3所示，其中主管和工字連梁均采用SHELL181單元劃分網格，并在組合柱端部將主管結點耦合在一起實現組合柱的整體鉸接。材料模型均采用理想彈塑性模型，彈性模量為206 GPa，泊松比為0.3，主管、連梁鋼材屈服強度分別為420 MPa、345 MPa。根據網格無關性分析結果，有限元模型中主管和連梁網格大小分別為100 mm、150 mm。

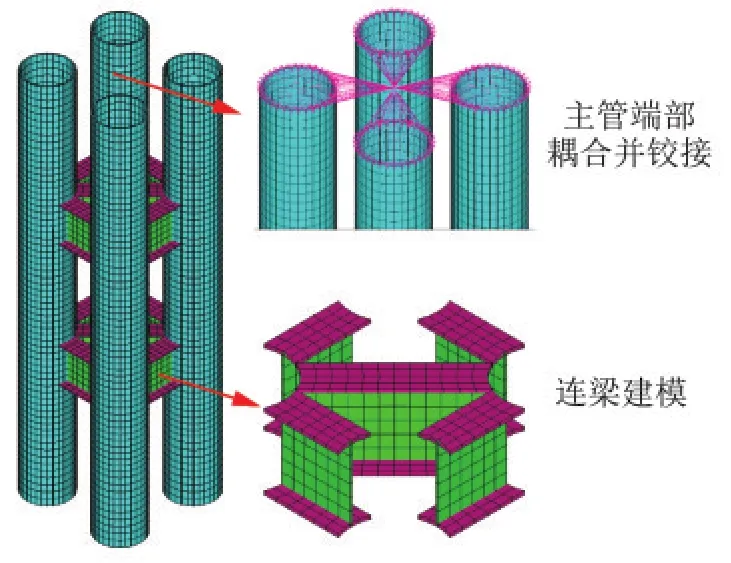
圖3 有限元模型Fig.3 Finite element model

彈性屈曲有限元分析中，在組合柱端部耦合節點施加集中力以模擬軸向荷載，并取第一階彎曲屈曲模態對應的臨界荷載作為該組合柱的彈性屈曲荷載。彈塑性屈曲有限元分析中考慮了材料非線性、幾何非線性以及初始缺陷。由于輸電塔組合柱長細比較小，初偏心的初始缺陷對組合柱承載力的影響較大[1，12]，因此根據文獻[1]將組合柱的初始缺陷取為

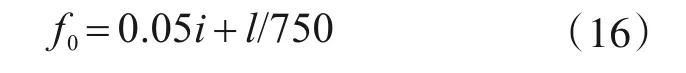
其中，初始偏心通過在柱兩端加載彎矩進行施加，初始彎曲通過一致模態法施加，輸電塔組合柱彈塑性穩定承載力根據非線性分析荷載-位移曲線的峰值確定。

2.1 彈性屈曲荷載對比

在組合柱彈性屈曲有限元分析中，當λ＜10時組合柱的第一階屈曲模態可能為主管的局部失穩或局部失穩與整體彎曲失穩的組合。為了使結果對比更有意義，在后續分析中將只列出第一階屈曲模態為組合柱整體彎曲的結果。

圖4、圖5分別給出了式（4）、式（3）計算得到的組合柱彈性屈曲荷載與有限元分析結果的相對誤差，其中負號表示比數值結果小。整體來看，式（3）和式（4）的相對誤差隨著組合柱長細比的減小而增大。在λ＜40時，不考慮綴板剪切變形[式（4）]的結果明顯大于有限元結果，且這種偏差隨著間距比的增加而增大。而考慮綴板剪切變形[式（3）]的結果與式（4）相比則更偏于安全；雖然在分肢凈間距較大（dn=800 mm）時式（3）結果相較于有限元也會偏大，但整體偏大不超過5%。

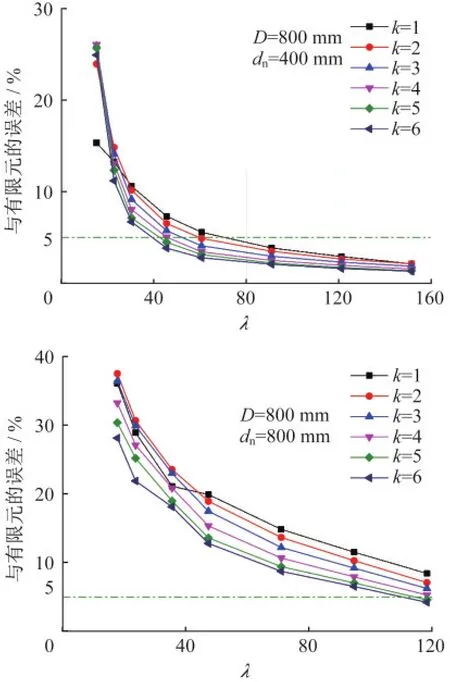
圖4 式（4）計算的彈性屈曲荷載與有限元對比Fig.4Comparison between Eq.（4）and finite element analysis

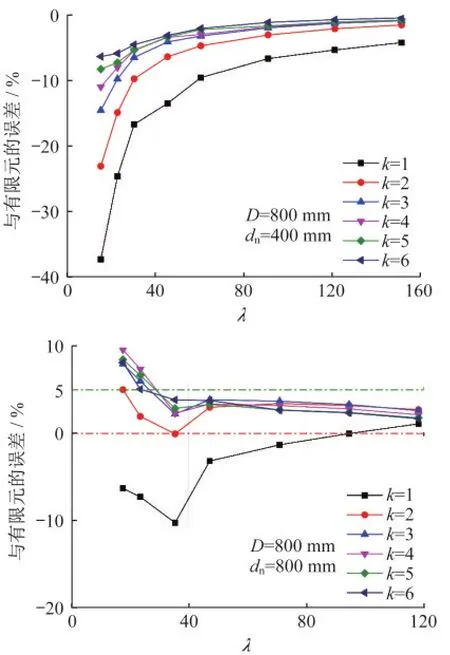
圖5 式（3）計算的彈性屈曲荷載與有限元對比Fig.5Comparison between Eq.（3）and finite element analysis

此外，式（3）、式（4）的相對誤差還隨著線剛度比的減小而增大。對于式（3）的對比結果，k＜3時相對誤差才會明顯增加。

2.2 彈塑性屈曲荷載對比

圖6給出了dn=400 mm、k=1時由換算長細比法、單肢驗算法和有限元分析得到的輸電塔組合柱柱子曲線。在應用換算長細比法時分別按式（3）、式（4）計算換算長細比。可以看到，采用式（3）的換算長細比法得到的組合柱穩定承載力更偏于安全，而采用式（4）的換算長細比法和單肢驗算法與有限元分析結果接近。

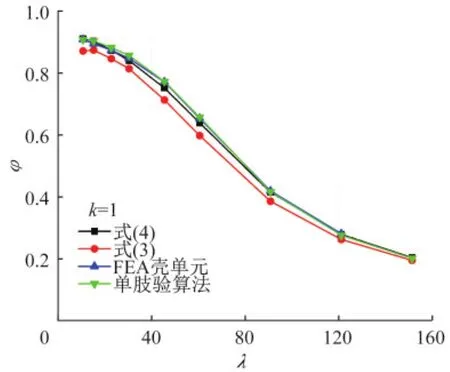
圖6 輸電塔組合柱柱子曲線（dn=400 mm，k=1）Fig.6 Column curves（dn=400 mm，k=1）

圖7給出了不同設計方法與有限元結果的相對誤差以作詳細對比，其中負值表示計算結果與有限元相比偏小，即偏于安全。總體而言，采用按式（3）、式（4）設計的換算長細比法和單肢驗算法與有限元結果相比誤差都相對較小。其中按式（4）設計的換算長細比法與有限元結果偏差最小，但在λ＜20時可能偏于不安全；按式（3）設計的換算長細比法整體偏于安全，但在λ＞30時相對誤差較大；單肢驗算法結果與有限元結果相比整體偏于不安全，這表示在本研究參數范圍內和初始缺陷條件下組合柱彈塑性穩定承載力不易由分肢失穩控制。此外，線剛度比k=3時換算長細比法結果的相對誤差與k=6時接近，表明該方法在小線剛度比條件下的適用性。

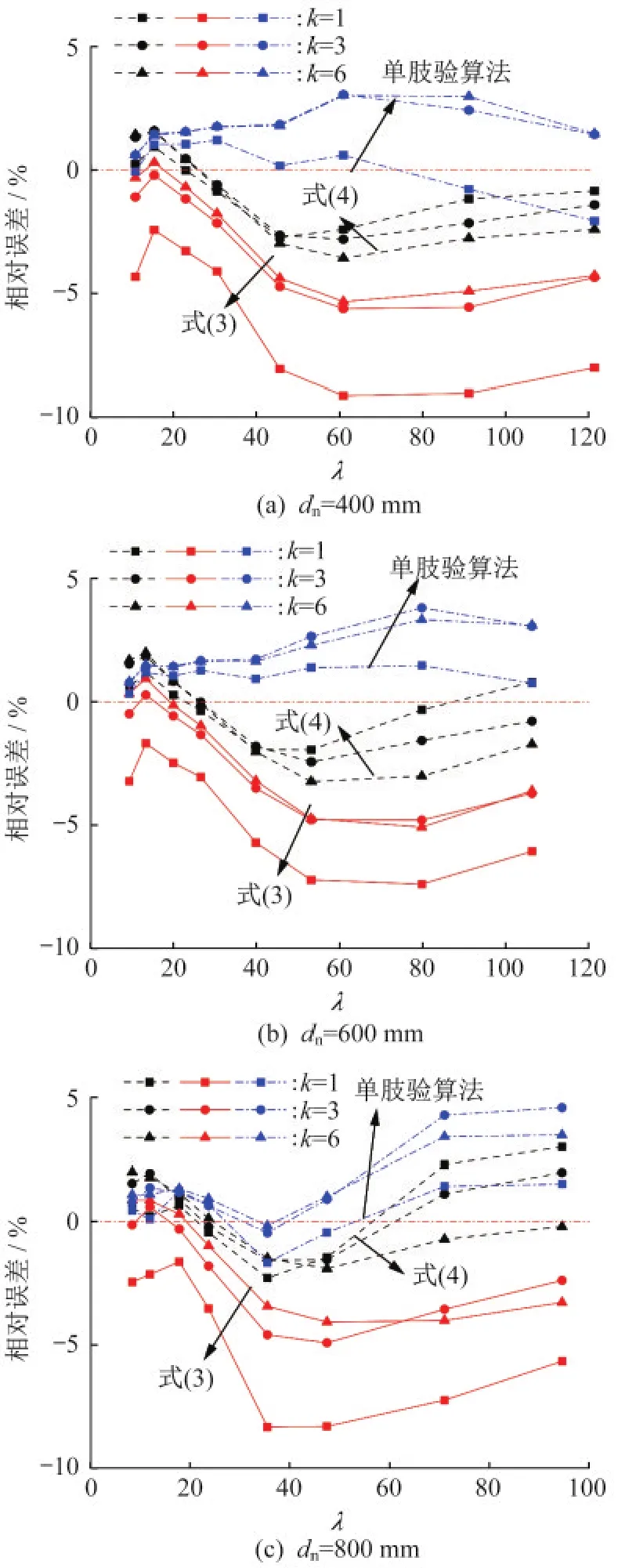
圖7 彈塑性屈曲荷載計算式與有限元對比Fig.7 Comparison between equivalent slenderness ratio method，chord-checking method and finite element analysis

2.3 線剛度比影響

采用有限元分析得到線剛度比為k時組合柱彈塑性屈曲荷載Ncrk，并以k=6時的屈曲荷載Ncr6為基準計算k＜6時組合柱承載力相對變化，結果如圖8所示。顯然，隨著輸電塔線剛度比的減小輸電塔組合柱彈塑性穩定承載力逐漸降低，并且k越小這種降低趨勢越明顯。總的來看，當線剛度比不小于3時承載力降低最大為3%，因此考慮經濟性要求組合柱連梁線剛度宜取為3。

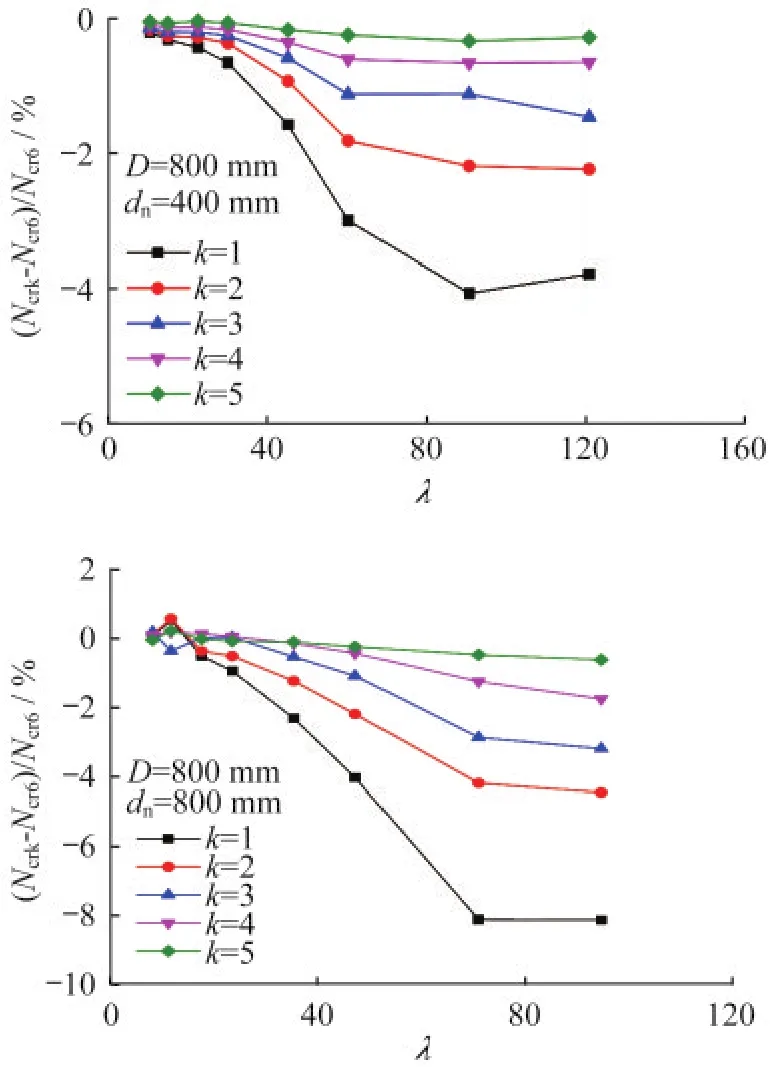
圖8 不同線剛度比下組合柱承載力較k=6時的變化Fig.8 The change of elastoplastic stability bearing capacity withkdecrease（compared withk=6）

3 算 例

本部分結合蘇通大跨越四鋼管組合柱輸電塔案例，對組合柱彈塑性承載力設計方法進行對比驗證。蘇通大跨越輸電塔鋼管塔型方案如圖1所示。該塔型方案中四鋼管組合柱的具體參數如表1所示，其中組合柱線剛度比均為3。

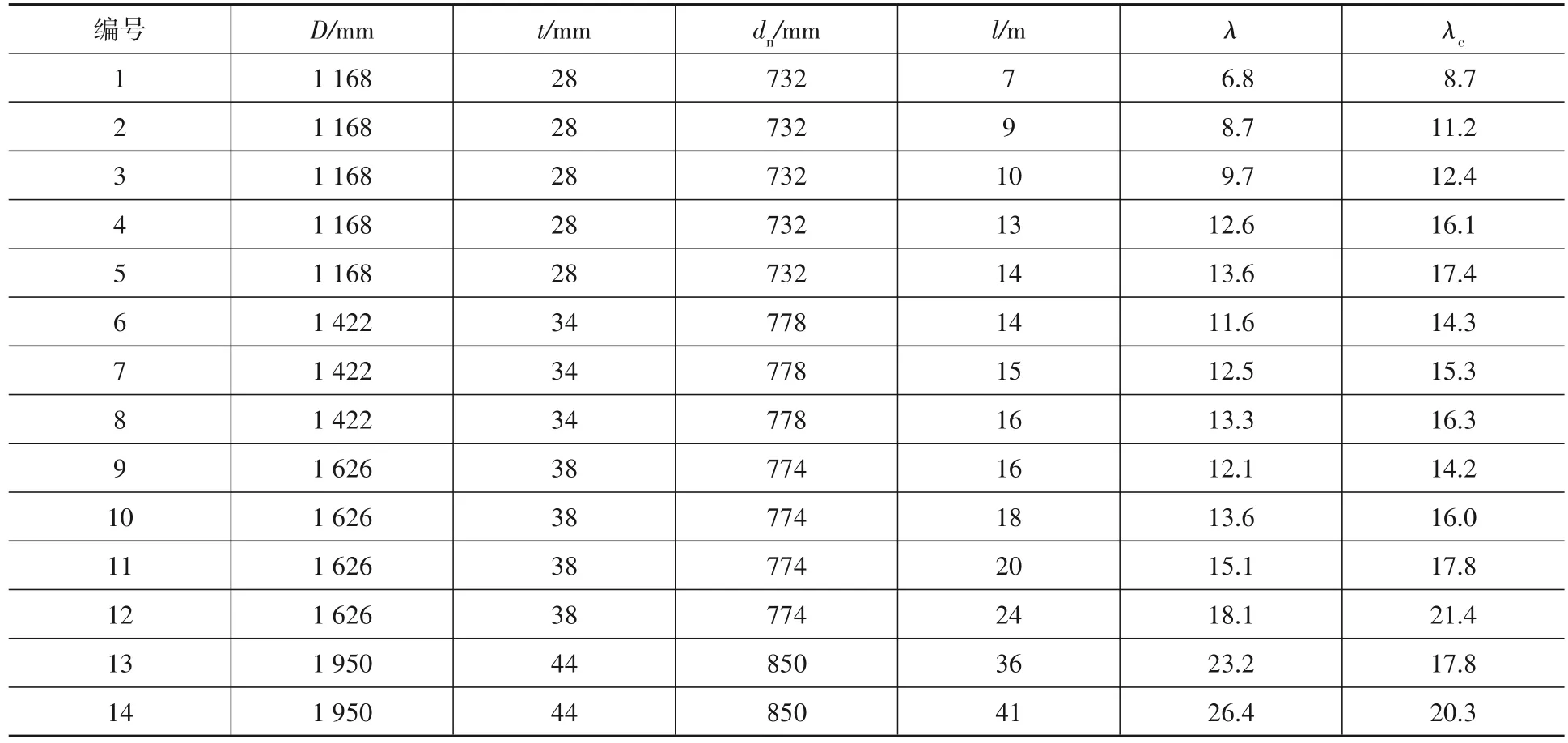
表1 四管組合柱參數Table 1 The parameters of four-tube built-up column

針對表1所示的不同組合柱，分別采用按式（3）、式（4）設計的換算長細比法和單肢驗算法得到其穩定系數，并與有限元分析結果進行對比，結果如表2所示。結果表明，按式（3）設計的換算長細比法與有限元結果相比更偏于安全；而按式（4）設計的換算長細比法和單肢驗算法與有限元結果相比誤差更小，但在λ＜10時可能偏于不安全。

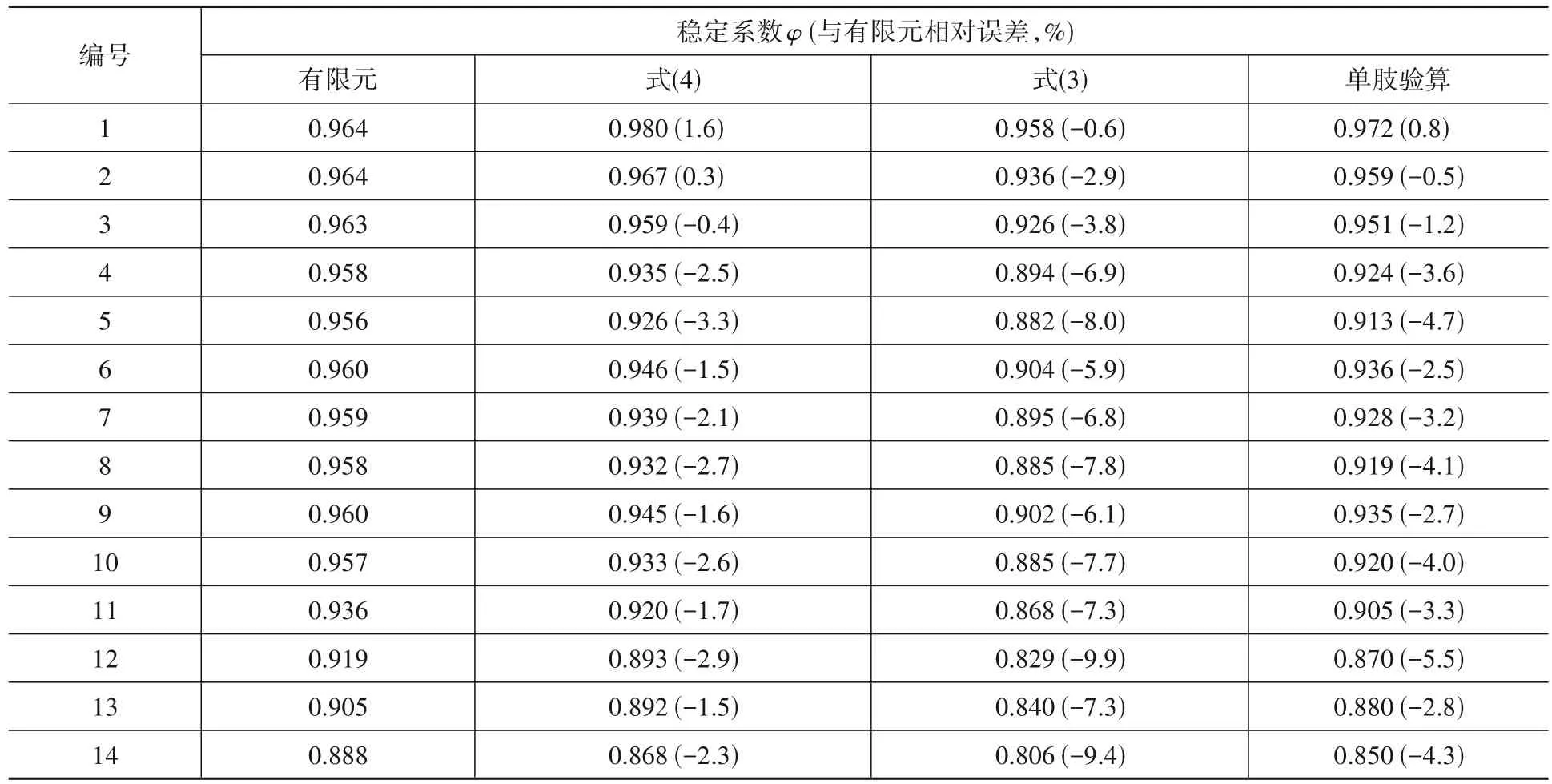
表2 不同設計方法與有限元的穩定系數對比Table 2 Comparison of stability coefficient between different design methods and finite element analysis

4 結論

本文根據輸電塔四鋼管組合柱的初始缺陷特點給出了考慮初彎曲和初偏心的單肢驗算法計算公式，并結合有限元計算分析對比了輸電塔四管組合柱彈性和彈塑性穩定承載力計算式的適用性，主要結論如下：

（1）組合柱彈性屈曲分析中，換算長細比公式考慮綴板剪切時[式（3）]的結果和不考慮時[式（4）]的結果相比，與有限元數值解符合得更好，建議按式（3）計算輸電塔組合柱彈性屈曲荷載。

（2）輸電塔四管組合柱線剛度比應不小于3，此時組合柱相對于k=6時的承載力降低最大為3%，且由換算長細比計算公式得到的結果誤差更小。

（3）組合柱彈塑性屈曲分析中，不考慮綴板剪切影響的換算長細比法結果與有限元結果偏差最小，但在組合柱長細比較小時可能偏于不安全；考慮綴板剪切影響的換算長細比法與有限元結果相比整體偏安全，但在λ＞30時可能過于保守；單肢驗算法結果與有限元結果相比整體偏大。

（4）在蘇通大跨越輸電塔組合柱計算中，當組合柱名義長細比小于10時建議考慮綴板剪切影響，長細比大于10時可按不考慮綴板剪切的換算長細比法或單肢驗算法計算。