基于粒子群算法的爆破振動速度智能預測方法

梁 娟

(武漢交通職業學院電子與信息工程學院，武漢 430065)

由于經濟效益高、操作性強及適應環境好等優勢，爆破技術被廣泛應用于交通設施、大型礦山開采、水電站及地下空間工程等大規模土建工程中[1-3]。然而，爆破工程在施工過程中，也會帶來各種負面的環境問題，例如爆破振動、爆破飛石、氣體污染等[4-5]。在實際爆破過程中，相關施工及研究人員需要采取各種控制措施減小爆破施工帶來的負面影響。其中，對于爆破施工周邊的既有構筑物來講，爆破引起的結構振動會不可避免地對其結構穩定性造成影響，尤其是對于抗震防護等級差的居民建筑，較小的地面振動就可能誘發共振現象，嚴重影響民用建筑的使用安全。因此，在實際爆破施工過程中，準確預測爆破施工引起的地面振動，進而合理采用施工技術對保護既有建筑結構的使用安全具有重要意義。

目前，國內外學者對爆破振動的預測研究主要從現場實測數據擬合、數值模擬及智能算法預測幾個方面展開。薩道夫斯基公式及經典的USBM模型(United States Bureau of Mines)常常被研究者用來預測爆破振動速度的衰減規律；Indian Institute of Standards等[6-9]經典模型也被用來預測爆破振動速度。王海龍等[10-11]依托上下交叉隧道工程，對爆破振動速度進行了最小二乘法擬合，并依據擬合結果提出了行之有效的爆破控制措施。數值模擬的方法也被用來預測爆破振動速度的變化規律。Qin等[12]通過ANSYS/LS-DYNA數值模擬三臺階爆破，并對效果進行了驗證；劉彥濤[13]則以回歸擬合及數值模擬對隧道爆破振動信號特征進行研究，詳細劃分爆破振動影響區域。近年來，與人工智能相關的方法也被應用于爆破振動速度的預測中[14-18]。比如，人工神經網絡(ANN)、自適應神經模糊推理系統(ANFIS)、多元回歸分析(MVRA)、基因表達編程(GEP)和其他回歸分析等程序被用于預測爆炸引起的地面振動。此外，深度學習、免疫算法及螞蟻算法等新型算法也常常受研究人員的青睞，且與其他算法相比，人工智能相關的預測手段展現出卓越的優勢。基于此，本文依托具體爆破工程實例[19]引入一種基于粒子群的智能優化預測系統，對爆破引起的地面振動進行研究，以期為振動速度的預測提供一種新思路。

1 粒子群算法

由Kennedy and Eberhart提出的粒子群算法原理是用來模擬鳥類聚集和魚類繁殖等生物社會行為，可以用來尋找問題的最優解。

粒子群算法由一群粒子組成，這些粒子可以根據最佳解決方案搜索個體最佳位置(pbest)和全局最佳位置(gbest)，因而該算法具有顯著智能性。簡而言之，每個粒子均會朝著個體最佳與全局最佳的方向運動。在粒子群算法中，每次迭代計算均根據粒子的位置和速度進行更新，其運動更新過程可以表示如下：

vi=ω×vi+c1r1(pbest-xi)+c2r2(pbest-xi)

(1)

式中：νi、xi分別為第i個粒子的速度、位置；ω為慣性權重；c1和c2為學習因子；r1和r2為[0,1]之間的均勻隨機數。

2 工程實例驗證

2.1 工程實例概況

1)工程實例1。以某鐵路工程隧道爆破工程實例為工程背景，隧道進入下穿區域前，在村莊內部選取合適的地面振動監測點，完成自動化監測，組建的光纖監測系統如圖1所示。選取具有代表性的監測結果進行研究，監測結果如表1所示。

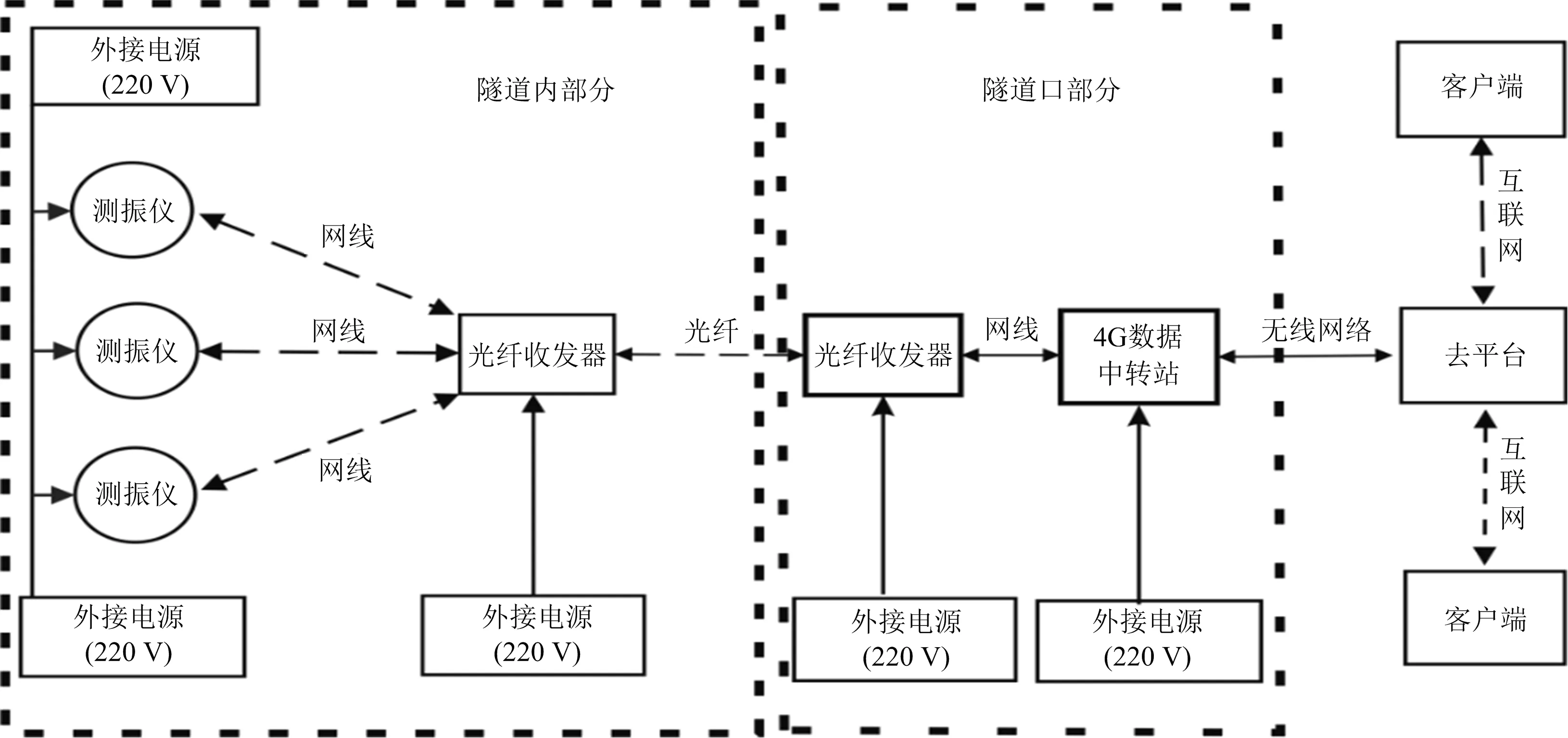
圖1 自動化監測系統Fig.1 Automatic monitoring system

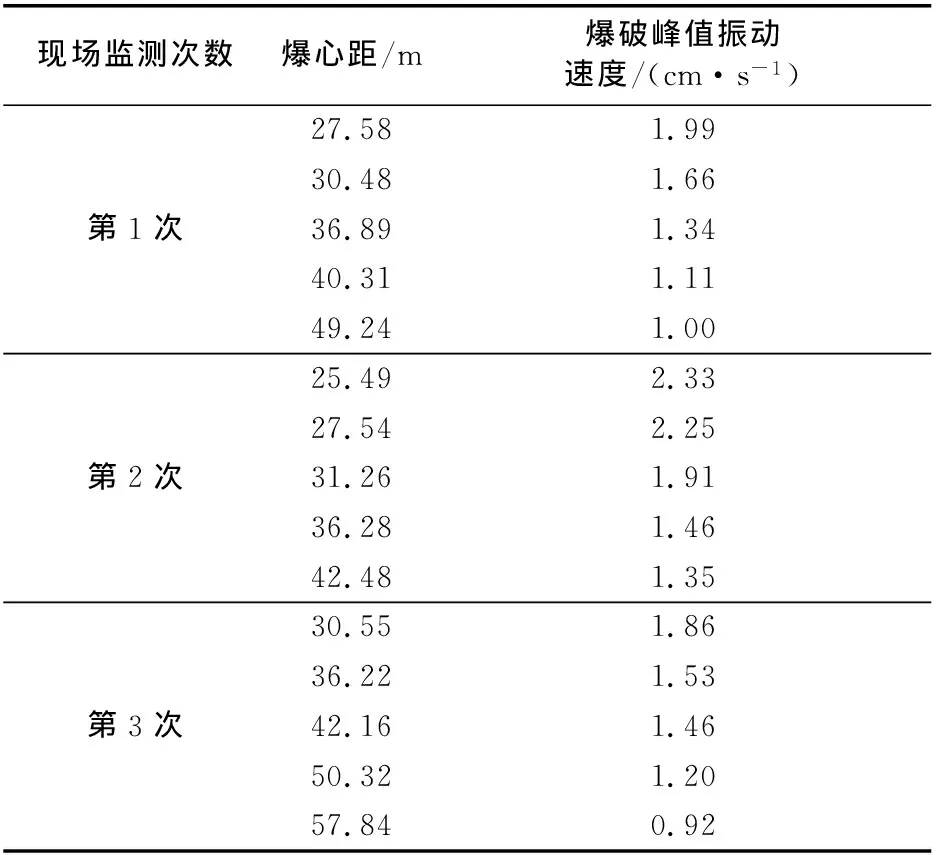
表1 爆破峰值振動速度及相關參數

2)工程實例2。依托某交叉隧道爆破工程進行既有隧道爆破振動速度預測工作，新建隧道爆破施工下穿既有鐵路隧道，而爆破施工引起的既有隧道的結構振動會對列車運營造成不利影響。基于王海龍等[11]及Zhao等[20]的實測方法，既有隧道爆破振動速度如表2所示。

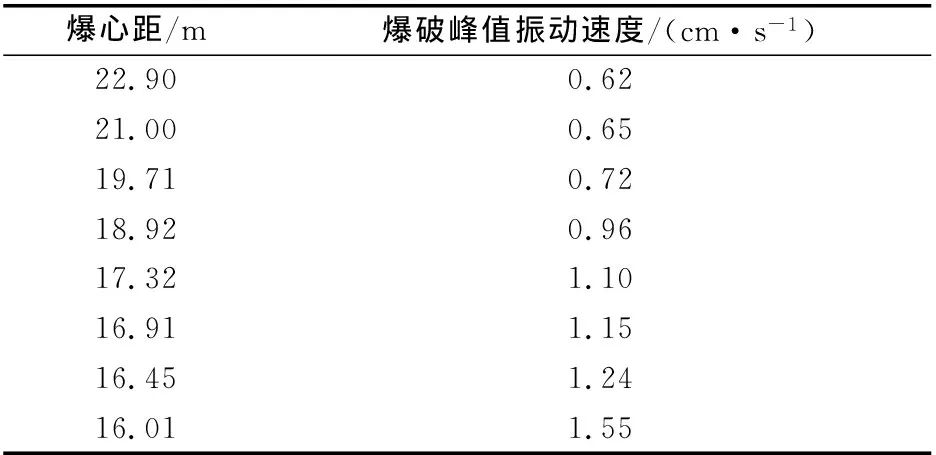
表2 既有隧道爆破振動速度

2.2 預測方法

在上述2項工程中，粒子群算法被提議用于預測爆破振動速度。為了評估所提出的粒子群智能優化水平精度，薩道夫斯基公式和USBM模型也被使用和開發。

1)USBM模型預測。在爆破振動速度預測領域，USBM是最常見的經驗方程，被許多爆破工程所廣泛使用。USBM模型表述如下：

(2)

式中：v為爆破振動速度；Q為最大單響藥量；R為爆心距；K和α為與爆破振動速度有關的系數。基于式(2)通過最小二乘法對爆破振動數據進行擬合，擬合結果為

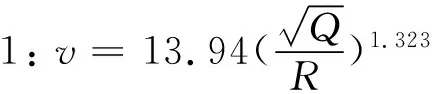
(3)

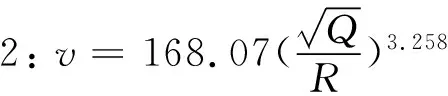
(4)

2)薩道夫斯基預測。薩道夫斯基公式是通過量綱分析的方法得到的，大多數國內學者利用此公式對爆破振動速度進行預測：

(5)

基于式(5)通過最小二乘法對爆破振動數據進行擬合，擬合結果為

(6)

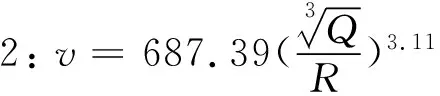
(7)

3)粒子群智能優化預測。為了估算爆破振動速度，開發粒子群優化指數函數預測模型。以最大單響藥量Q和爆心距R作為模型的輸入，而爆破振動速度v作為輸出參數。在粒子群優化建模的第1步，為了提高模型診斷輸入和輸出之間關系的能力，對輸入和輸出參數的數值進行了歸一化處理。其中，粒子群優化的指數函數預測模型表示為

v=α1+α2Qβ+α3RγV=α1+α2Qβ+α3Rγ

(8)

式中：α1、α2、α3為對應傳統預測模型中的場地系數K；β、γ為與裝藥量及爆心距有關的指數，其中，γ與傳統模型中的衰減系數意義相近，可以認為式(8)為傳統模型的另一變式。

依據粒子群優化原理，首先需要確定適應度函數，基于最小二乘擬合的算法推導，選擇適應度函數的目的是為了使實測數據與回歸擬合值的誤差的平法最小。因此，適應度函數可以選取如下：

(9)

式中：vi為實測爆破振速；n為實測數據個數；v′i則可以根據式(8)計算得到。

利用MATLAB中的PSO優化工具箱進行粒子群優化計算，其中粒子群規模為250，慣性權重為0.9，學習因子c1、c2皆取2，最大迭代次數為1 000。

實例1計算得到特征參數分別為：α1為7.398，α2為0.028，α3為0.901，β為0.616，γ為0.75，則式(8)可轉換為

v=7.398+0.028Q0.616+0.901R0.75

(10)

式(10)的擬合效果如圖2所示。

圖2 基于粒子群算法的工程實例1智能優化預測效果Fig.2 Prediction effect of engineering example 1 based on particle swarm optimization algorithm

實例2計算得到特征參數分別為：α1為0.066，α2為23.37，α3為899 9，β為-2.145，γ為-3.052，則式(8)可轉換為

v=0.066+23.27Q-2.145+899 9R-3.052

(11)

2.3 預測效果對比及討論

為驗證粒子群優化的爆破振速的預測效果，對3種擬合方法的預測效果進行對比，主要針對相關系數的平方(r2)及均方根差(RMSE)進行對比。其中，RMSE計算方法如下：

(12)

相關系數的平方r2越接近1，均方根差RMSE越小，則說明預測效果越好。3種方法的預測統計量如表3所示。

表3 3種方法的預測統計量

由表3可知，實例1、實例2采用粒子群算法得到的r2分別為0.967、0.947，更接近于1，皆大于采用USBM得到的r2值0.907(實例1)、0.810(實例2)和薩道夫斯基公式得到的r2值0.891(實例1)、0.710(實例2)；實例1、實例2采用粒子群算法得到的RMSE分別為0.14、0.22，更接近于0，皆小于采用USBM得到的RMSE值0.25(實例1)、0.41(實例2)和薩道夫斯基公式得到的RMSE值0.29(實例1)、0.70(實例2)。通過粒子群優化的模型所得到的r2最大，RMSE最小，與其他兩種擬合方法相比，擬合效果最好。

由于USBM模型方法、薩道夫斯基公式方法是通過最小二乘法進行擬合，而粒子群優化方法采用的是基于最小二乘擬合算法推導的適應度函數方法進行擬合，擬合方法存在差異。因此，為了證明粒子群算法的優越性，以工程實例1為例，利用最小二乘法對式(10)進行擬合，擬合結果如圖3所示。

圖3 最小二乘法按按擬合結果Fig.3 Fitting effect of least square method

由圖3可知，最小二乘擬合效果r2=0.912，盡管采用最小二乘法擬合的數據小于粒子群適應度函數優化得到的0.967，但仍然優于USBM模型方法、薩道夫斯基公式方法，進一步驗證了本文引入的基于粒子群算法的智能預測方法效果較好。

3 結論

1)人工智能算法在爆破振動速度的預測過程中顯示出較為明顯的優勢，其依托現今主流的機器算法，可以更好服務于爆炸誘發的地面振動的預測工作中。

2)與傳統爆破振動預測模型相比，基于粒子群智能優化的指數模型得到的相關系數r2更接近于1；均方根差RMSE最小，預測精度最佳。可見，引入基于粒子群的智能優化預測思路可以被應用于爆破引起的地面振動的預測研究中。