大模數齒輪齒條機構建模與靜力學分析*

盛洪瀟

(三峽大學 機械與動力學院，湖北 宜昌 443002)

0 引 言

作為大國重器的典型代表，三峽升船機和龍源振華叁號都是大模數齒輪齒條驅動式起升工作平臺[1]。大模數齒輪齒條起升機構作為其關鍵零部件具有傳動效率高、傳動精度高、結構緊湊、使用壽命長等優點。諸多優點使得齒輪齒條機構廣泛應用于大型機械上,如礦山機械、石油機械、升船機械、海洋平臺等大型升降設備。

王振[2]將三峽升船機中的大模數齒輪齒條機構作為分析對象，使用理論計算與有限元分析結合的方法，推斷出改變修正系數選取方法后的國標計算公式。

唐文獻等[3]針對風電安裝船齒輪齒條式升降系統，建立了超大模數齒輪齒條有限元分析模型，研究了齒輪的變位系數、壓力角、模數等參數對齒輪齒條彎曲強度及接觸強度的影響。

為了研究齒輪齒條機構的接觸應力，張興權等[4]運用齒輪承載能力計算方法中的接觸應力計算公式，求解了齒輪齒條機構在不同位置嚙合時的接觸應力。

筆者主要對不同工況參數條件下的齒輪齒條傳動系統展開研究，結合理論公式計算與計算機軟件分析，建立齒輪齒條機構的三維實體模型，研究在對應工況下齒輪彎曲應力和接觸應力的大小、分布規律。

1 齒輪齒條材料參數與設計參數

齒輪傳動機構工況復雜，并且在機械設備的工作中發揮十分重要的作用，為了保證設備的安全運行，需要對不同工況條件下的齒輪強度進行校核，一般要計算齒輪的齒根彎曲應力和齒面接觸應力，對比這兩個應力是否在材料的安全范圍之內，以此來驗證齒輪的強度是否滿足要求[1]。

本文所分析研究的齒輪齒條材料參數及設計參數如表1所列。

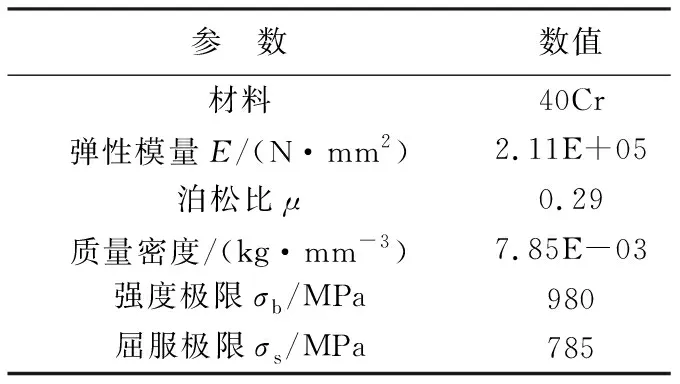
表1 齒輪齒條的材料及設計參數

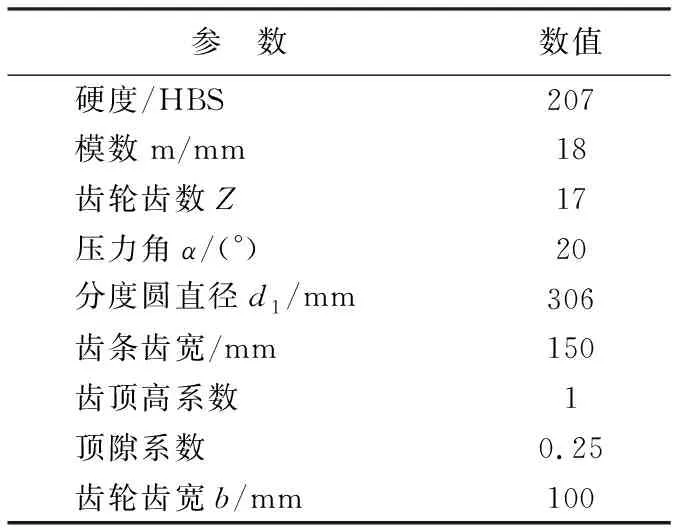
續表1 齒輪齒條的材料及設計參數

參考齒輪齒條升降裝置的實際工況，設置6組不同工況條件下的齒輪切向力Ft，依據式(1)，計算出齒輪運行時所受力矩t0的大小，為了便于計算和分析，將使用輸入力矩t1來進行理論計算和有限元分析。6組工況參數如表2所列。

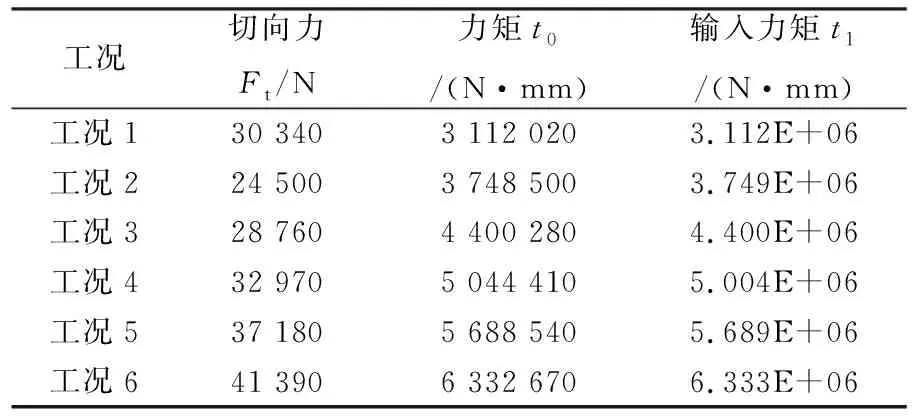
表2 齒輪齒條的工況參數

t0=Ftd1/2

(1)

式中：t0為齒輪工作時受到的力矩；Ft為齒輪切向力；d1為齒輪分度圓直徑。

2 理論計算

齒輪齒條強度的理論計算部分主要包括彎曲應力計算和接觸應力計算[5]，本文中采用ISO公式[6]來計算齒輪彎曲應力，采用30°切線法確定齒根彎曲應力的危險截面[7]，齒輪的齒根彎曲應力計算公式：

(2)

式中：KF為彎曲強度計算的載荷系數；Ft1為齒輪圓周力；YFa為載荷作用于單對齒嚙合區上屆點時的齒形系數，與齒制、變位系數和齒數有關，與模數無關；Ysa為載荷作用于單對齒嚙合區上界點時的的應力修正系數；Yε為齒輪彎曲強度計算的重合度系數；b為齒輪齒寬；m為齒輪模數。

將六種工況的參數帶入式(2)可得齒根彎曲應力如表3所列，這些值作為齒輪彎曲應力的理論計算結果，將與后續的有限元分析結果做比較。

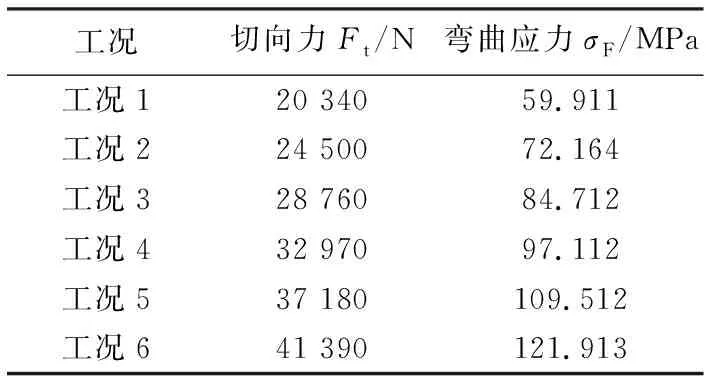
表3 齒輪彎曲應力的理論計算值

齒輪接觸應力采用Hertz理論的計算公式，為了使計算結果更加符合實際，學者們引入更多參數對公式進行了修正[8]，最終得到了現在的齒輪齒面接觸應力計算公式(3)：

(3)

式中：σH為齒輪的齒面接觸應力；ZH為節點區域系數；ZE為齒輪材料的彈性影響系數；Zε為齒輪重合度系數；Zβ為齒輪螺旋角系數；b為齒輪齒寬；υ為齒輪傳動比，齒輪齒條傳動;υ取無窮大；KH為齒輪接觸強度計算的載荷系數。

將六種工況參數帶入式(3)可得齒面接觸應力如表4所列，這些值和表3中的值作為齒輪齒根彎曲應力和齒面接觸應力的理論計算結果，將與后續有限元分析結果作對比。

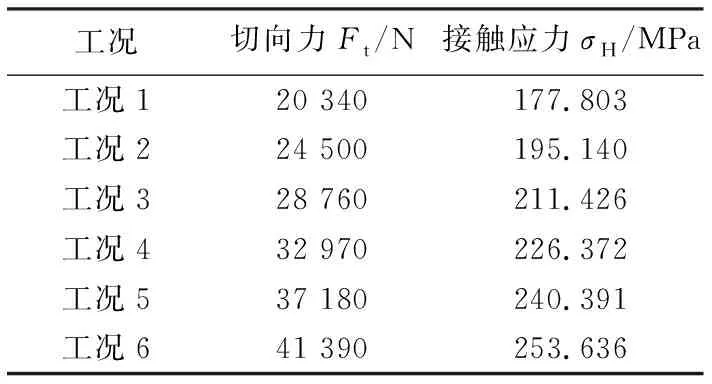
表4 齒輪接觸應力理論計算值

3 建模與靜力學分析

有限元法核心思想是把連續的結構分散成有限多個離散的單元，對每個單元分別進行計算后再組合到一起就能得到整體的力學特性，將復雜的實際問題大為簡化并得出比較精確的分析結果。文中采用SolidWorks軟件來建立齒輪齒條實體模型，再利用軟件相關聯的端口將模型導入ANSYS軟件展開分析。所建立的齒輪齒條嚙合模型如圖1所示。

圖1 齒輪齒條嚙合模型

接下來就是建立有限元分析模型，施加約束條件和載荷等。為了提高分析精確度，需要對接觸區域的網格進行加密，使用級別3加密后得到的總劃分節點41449個，總劃分單元24835。處理完之后的齒輪齒條模型如圖2所示。如圖3所示，靜力學分析齒輪的齒根彎曲應力和齒面接觸應力需要將齒輪齒條固定，為了方便給齒輪輸入力矩，在靜態結構中給齒條施加固定支撐，給齒輪施加圓柱形支撐，根據表2的工況參數輸入力矩的大小和方向然后進行求解。

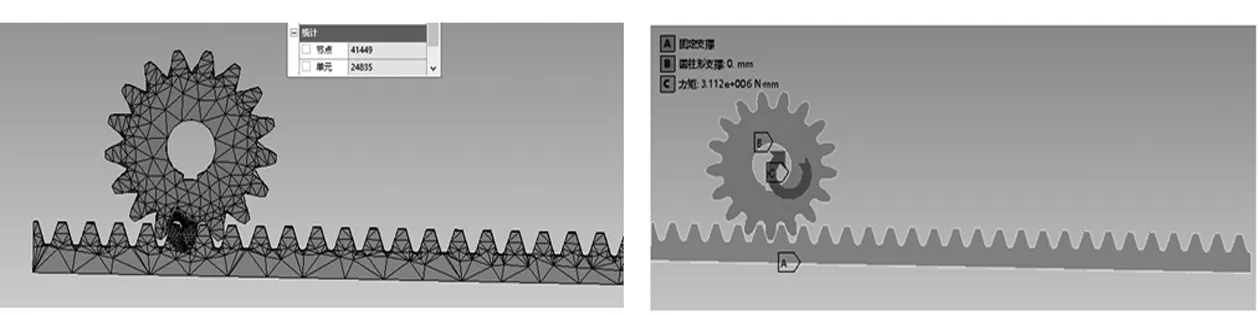
圖2 網格劃分模型 圖3 工況1求解模型

齒輪齒條傳動機構在工況1條件下產生的齒根彎曲應力最大值為53.509 MPa，如圖4所示，圖5為工況1對應的齒面接觸應力云圖。

圖4 工況1彎曲應力云圖 圖5 工況1接觸應力云圖

從工況1到工況6，齒輪的切向力Ft在不斷增加，相應地，齒輪的齒根彎曲應力和齒面接觸應力也在不斷增加。根據表2中工況參數改變輸入力矩，在6組工況條件下，通過靜力學分析所得到的齒輪的彎曲應力和接觸應力如表5所列。將有限元分析所得數據和理論計算結果進行對比，整理之后得到表6和表7結果。

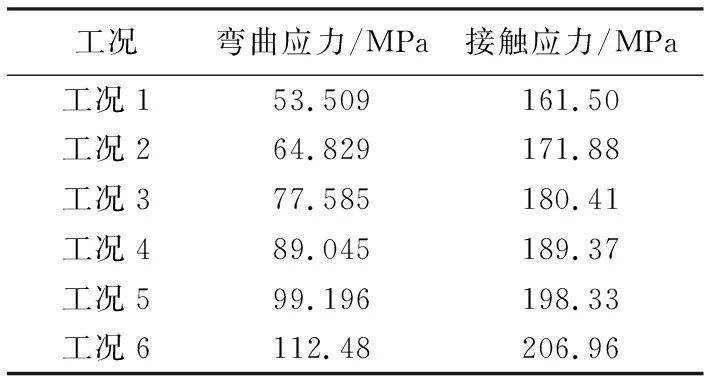
表5 彎曲應力與接觸應力有限元分析結果

表6 齒輪彎曲應力對比

表7 齒輪接觸應力對比

不管是齒輪彎曲應力還是齒面接觸應力，理論計算結果和靜力學分析結果相差在10%左右，考慮到誤差因素的影響，可以把它們近似看作相等，兩種方法互為證明，驗證了采用這兩種方法來計算齒輪彎曲強度和接觸強度的可行性和準確性。

4 結 論

文中針對齒輪齒條起升機構，參考實際情況，模擬設置了6組不同的工況，對齒輪的彎曲強度和接觸強度展開了理論計算和有限元分析，并將得到的結果進行了對比，得到了以下結論。

(1) 選擇“ISO齒輪彎曲應力公式”和“Hertz接觸理論”對齒輪彎曲應力和接觸應力進行了分析計算，發現6組工況條件下算得的齒輪的彎曲、接觸應力隨切向力的增大而增大。

(2) 建立了齒輪齒條傳動機構的裝配模型，進行了靜力學分析，通過有限元分析求解了6組工況下的齒輪彎曲應力及接觸應力并將結果與理論計算進行對比。分析發現齒輪彎曲應力最大值出現在齒根位置，接觸應力主要分布在輪齒表面，并且理論計算與有限元分析得出的數據差值在10%左右，驗證了理論計算法和有限元分析法求解齒輪彎曲強度和接觸強度的可行性和準確性。