風力發電機塔筒結構仿生設計分析*

李 村，文 鵬

(甘肅酒鋼集團西部重工股份有限公司，甘肅 嘉峪關 735100)

0 引 言

塔筒為風力發電機的主要承載部件，其承載能力直接影響到風力發電機的發電效能。塔筒穩定性問題隨著風力發電機的容量和高度增加而表現愈加明顯[1]。塔筒失效形式多表現為屈曲破壞，在極端工況下塔筒此類問題表現較為突出[2]。提高塔筒結構穩定性，對于風力發電機的安全運行有著重大的意義。

仿生結構領域的研究及應用可以為塔筒的設計提供新的思路，仿生設計可將生物的優異功能賦予至機械設備，使其具備良好的機械性能。在相似的受載環境下，沿海岸分布的棕櫚樹表現出優異的抗風性及穩定性，棕櫚樹為高大型植物，其樹干是多段式結構，能夠抵擋多種風載荷，甚至在颶風下屹立不倒，具有良好的剛柔耦合性。棕櫚樹維管束的存在有助于提升整體強度，使棕櫚樹長勢更高，有研究證實棕櫚樹的力學性能與維管束纖維直徑有直接關系。棕櫚樹維管束纖維應力-應變曲線可分為彈性階段、塑性階段和停滯階段，由于維管束的結構特點使其具有優異的機械性能，表現出良好的抗風能力。通過大量文獻閱讀發現，棕櫚樹的力學性能與維管束纖維直徑有關。將棕櫚樹不同部位的維管束纖維提取并測試其機械性能，結果表明：不同部位的維管束纖維機械性能有所不同。在此基礎上，以維管束纖維為基體制備某復合材料進行試驗。試驗證明：當維管束纖維含量達到10%時，該復合材料的彈性模量最高[3]。在風力機塔筒結構仿生方面，為提高塔筒整體的剛度、強度，通過仿棕櫚植物的內部結構，將塔筒內部腹板設計成雙層六邊形蜂窩類維管束結構，結果表明，仿生塔筒塔頂位移減少為原塔筒的38%，最大應力下降19%[4]。考慮到棕櫚類樹干結構與大型風力機塔筒結構的相似性，在其實驗研究的基礎上，從材料屬性分布和幾何結構分布兩個方面進行塔筒仿生設計分析[5]。

綜上所述，筆者將棕櫚樹維管束結構應用至塔筒設計中，構建仿棕櫚樹維管束的仿生塔筒。利用有限元數值法計算仿生塔筒和原塔筒靜態響應、固有頻率及穩定性，并對二者進行比較分析，為塔筒的結構仿生設計提供理論依據。

1 塔筒仿生設計

以某企業2MW風力發電機錐形塔筒為研究對象，塔筒由3法蘭連接4段式錐形筒和基礎環組成。輪轂中心距地面80 m，塔筒材料為Q345E，總重172.51 t，塔身由四段錐形筒組成，尺寸如表1所列，錐形筒之間由法蘭及高強度螺栓連接。塔筒底部外徑為4 200 mm，底部壁厚為42 mm,塔筒頂部的外徑3 005 mm,頂部壁厚為22 mm。

表1 原塔筒尺寸

棕櫚樹多生長在海邊，憑借其自身優異的結構性能可抵抗強風，甚至颶風。考慮到風力機塔筒在運行時所受的結構、載荷、約束與棕櫚樹存在著相似性。為提高風電機組塔筒的力學性能，借助結構仿生學思想，依據棕櫚樹維管束結構設計帶有維管束結構的風力發電機仿生塔筒。依據棕櫚樹維管束結構幾何特征，設計仿生塔筒維管束結構。在每一段錐形筒的底部法蘭的上方增加仿棕櫚樹維管束結構，仿生塔筒帶4個維管束結構。仿生塔筒維管束結構由中心孔、雙邊蜂窩狀六邊形及通道構成。中心孔半徑和六邊形邊長記為r，仿生塔筒維管束結構半徑記為R，則它們之間的幾何關系為r=1/10R[3]。仿生塔筒維管束幾何結構及位置如圖1所示。

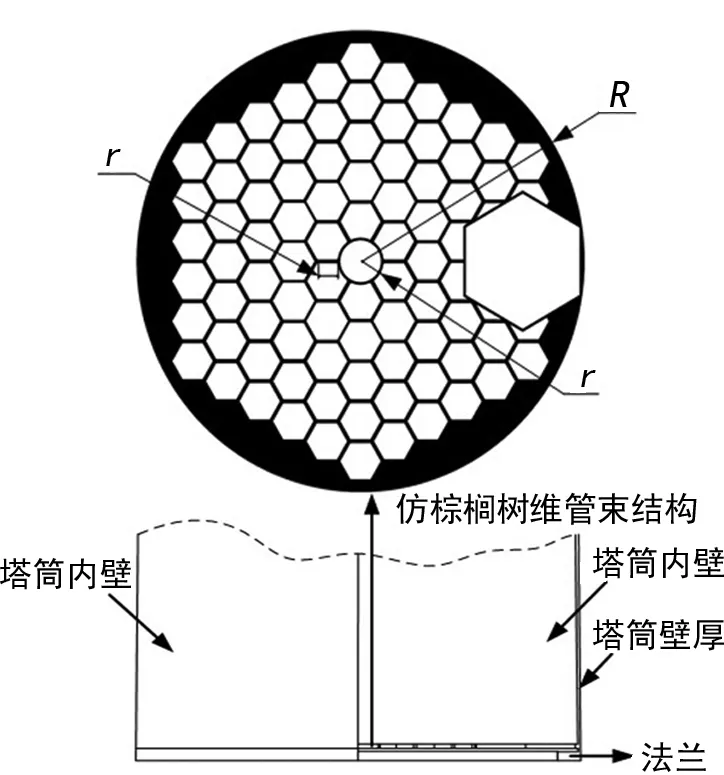
圖1 仿生塔筒維管束幾何結構及位置

根據表1和圖1建立仿生塔筒實體模型和有限元模型。在此基礎上計算仿生塔筒在極端工況下的靜態響應、穩定性及固有頻率。

2 仿生塔筒分析

為計算仿生塔筒的固有頻率、極端工況下的靜態響應及其穩定性，需建立仿生塔筒的有限元模型。在建立仿生塔筒有限元模型時，其材料選取Q345，采用以六面體為主導的機械結構劃分方式對原塔筒及仿生塔筒進行網格劃分，網格尺寸為200 mm,共生成網格單元數276 300個，節點數569 240個。每段錐形筒法蘭連接處采取綁定約束，其法蘭連接面處采用多點約束算法，仿生塔筒有限元模型如圖2所示。

圖2 仿生塔筒有限元模型

2.1 仿生塔筒固有頻率

為驗證仿生塔筒結構的安全性，擬計算仿生塔筒的固有頻率。對仿生塔筒和原塔筒進行固有頻率計算時，采用本文所建立的仿生塔筒有限元模型，并在仿生塔筒基礎環處施加固定約束。由于塔筒為多自由度系統，計算其所有固有頻率耗時，低階固有頻率對其結構影響更大[6]，因此本研究提取原塔筒及仿生塔筒的前6階固有頻率，如表2所列。

表2 原塔筒及仿生塔筒固有頻率/Hz

仿生塔筒及原塔筒的一階振型沿X方向擺振，其二階振型沿Y方向擺振。為避免塔筒結構發生共振，在設計時要確保塔筒的固有頻率遠離風輪轉速頻率1P和葉片的通過頻率3P(三倍風輪轉速頻率)的±10%[7]，風輪主要參數如表3所列。

表3 風輪參數

通過表2和表3可知，仿生塔筒及原塔筒的一階、二階頻率均遠離風輪正常頻率區間和葉片通過頻率區間約15%，因此原塔筒及仿生塔筒不會發生共振現象，原塔筒和仿生塔筒結構合理且安全可靠。

2.2 仿生塔筒靜態分析

設計仿生塔筒時需考慮極端工況的影響。基于塔頂坐標系，計算塔筒在四種極端工況下的載荷[2]，分別是極端湍流模型(DLC1.3)、極端風切變模型(DLC1.5)、極端陣風模型(DLC3.2)和極端風速模型(DLC6.1)，四種極端載荷如表4所列。

為研究仿生塔筒的靜態響應，應用有限元數值分析法，計算原塔筒模型和仿生塔筒模型在表4極端工況下最大應力和塔頂位移，對比原塔筒和仿生塔筒在同等工況下靜態響應特性。

表4 極限載荷分布

對仿生塔筒進行靜態響應分析時，依據塔筒實際工況，在塔筒底部基礎環處施加一個固定約束，將風輪和風力機機艙的簡化集中質量點耦合至塔同頂部。采取塔頂坐標系，將表4極端載荷依次施加于仿生塔筒。原塔筒及仿生塔筒的在極端工況下塔頂位移響應和應力響應如圖3和圖4所示。

圖3 塔頂位移響應

圖4 塔筒最大應力響應

由圖3可知，在極端工況下，仿生塔筒塔頂位移響應均小于原塔筒。在DLC3.2即極端陣風工況下，仿生塔筒塔頂位移較原塔筒減少9.47%，在DLC6.1即極端風速工況下，仿生塔筒塔頂位移較原塔筒減少8.55%，可見仿生塔筒在DLC3.2工況下塔頂位移響應最小。由于維管束結構存在，使得仿生塔筒剛度提升，有效抵抗強陣風載荷對塔筒的沖擊，減少塔筒在極端工況下的位移響應。

由圖4可知，在極端工況下，原塔筒表現出最大應力為185.79 MPa。依據IEC61400-6 EDI規范[8]，取安全系數1.1，材料的最大許用應力為313.6 MPa，故原塔筒和仿生塔筒均符合強度要求。在DLC1.3、DLC1.5和DLC6.1下仿生塔筒和原塔筒應力分別減少9.82%、20.05%、2.84%，由于仿生塔筒維管束結構的存在使得其強度在此三種極端工況下得到提升。仿生塔筒使風力發電機在極端工況下能夠安全運行。

2.3 仿生塔筒穩定性

塔筒的穩定性和承載能力在很大程度上取決于自身的結構，因此有必要對塔筒屈曲穩定性進行計算。對原塔筒和仿生塔筒利用有限元數值分析法進行特征值屈曲分析。采用2.1小節中的約束條件及塔頂坐標系，不考慮機艙、風輪及塔筒自身的重力加速度，在塔筒頂部施加沿z軸反方向的單位載荷。完成初始條件的設置，求解原塔筒及仿生塔筒前2階屈曲特征值，如表5所列。

表5 原塔筒及仿生塔筒前兩階屈曲特征值

由表5可知，仿生塔筒一階屈曲載荷和二階屈曲載荷基本一致，主要由于其結構的對稱性所致。結構穩定性主要取決于一階臨界屈曲載荷，根據IEC-61400-6 ED1規范[9],基于殼體結構，屈曲安全因子γs為1.2，其屈曲安全系數小于1時，殼體結構趨于穩定。結構的屈曲安全系數為結構的最大軸向載荷和屈曲安全系數的乘積與一階屈曲臨界載荷的比。原塔筒和仿生塔筒在4種極限工況下的屈曲安全系數如圖5所示。

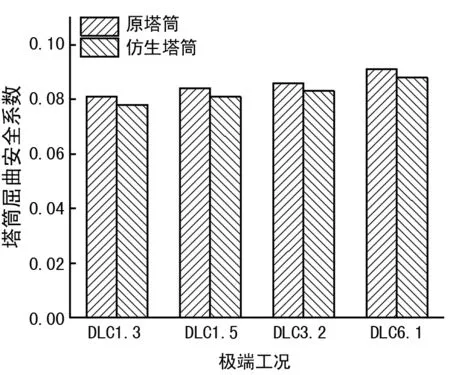
圖5 原塔筒及仿生塔筒屈曲安全系數

由圖5可知，在4種極端工況下，原塔筒和仿生塔筒安全系數都小于1，原塔筒和仿生塔筒均不會出現失穩的狀況。在DLC6.1工況下原塔筒和仿生塔筒屈曲安全系數分別為0.088、0.091，相比原塔筒仿生塔筒穩定性提升3.29%；DLC3.2工況下，仿生塔筒較原塔筒穩定性提升3.49%；DLC1.3和DLC1.5的工況下，仿生塔筒的穩定性優于原塔筒。從表5和圖5可知，維管束結構使得仿生塔筒穩定性優于原塔筒。維管束結構使得仿生塔筒不易在極端風環境下發生屈曲破壞，確保整個風力機運行安全。

3 結 論

以棕櫚樹為生物原型對風電機組塔筒結構進行仿生設計，設計出在每段錐形筒法蘭上方帶有維管束結構的仿生塔筒，并計算仿生塔筒及原型塔筒的固有頻率、極端工況下靜態響應和穩定性，分析結果總結如下。

(1) 采用有限元數值法計算了仿生塔筒及原始塔筒的前六階頻率，仿生塔筒和原塔筒的前兩階固有頻率均遠離正常頻率區間和葉片通過頻率區間約15%，表明仿生塔筒和原塔筒不會發生共振現象，結構可靠。

(2) 仿生塔筒在4種極端工況下，塔頂位移較原塔筒均減小，其中在DLC3.2下仿生塔筒位移減少更明顯。表明維管束結構使得仿生塔筒剛度提高，使其具備更強的抗風性。仿生塔筒在DLC1.5工況下表現出最小應力，仿生塔筒維管束結構使其強度得到改善。

(3) 仿生塔筒較原始塔筒屈曲載荷提升3.61%，與此同時，仿生塔筒在本文的極端工況下，屈曲安全系數均得以提升，表明維管束結構使得仿生塔筒的穩定性得到了提升。