APOS理論下的高三立體幾何復(fù)習(xí)建議

王娜

【摘 要】 APOS理論最早是由杜賓斯基提出的，是一種科學(xué)的建構(gòu)主義理論，這種理論強(qiáng)調(diào)了個(gè)人的重要性，個(gè)人想要得到結(jié)果，需要以旁觀者的角色參與到活動(dòng)中，能總結(jié)和反思活動(dòng)的方法、內(nèi)容、過(guò)程.在參與的過(guò)程中，能充分發(fā)揮自身的創(chuàng)造力，還能展現(xiàn)主觀能動(dòng)性.這可看出，APOS理論充分體現(xiàn)了學(xué)生在學(xué)習(xí)過(guò)程中的主體性，說(shuō)明學(xué)習(xí)過(guò)程是在經(jīng)歷充分的總結(jié)和反思之后的結(jié)果.數(shù)學(xué)學(xué)習(xí)的重要方式和途徑是個(gè)體能夠在活動(dòng)中有所經(jīng)歷，通過(guò)圖式階段、對(duì)象階段來(lái)建構(gòu)概念，在這其中，個(gè)體會(huì)產(chǎn)生抽象的思維，能夠主動(dòng)反思該階段學(xué)習(xí)的過(guò)程、方法，會(huì)意識(shí)到反思的重要性. 本文以高三立體幾何復(fù)習(xí)為例，分析APOS理論在數(shù)學(xué)教學(xué)中的應(yīng)用.

【關(guān)鍵詞】 APOS理論;立體幾何;高三數(shù)學(xué)

1 立體幾何復(fù)習(xí)背景分析

高三的學(xué)生已經(jīng)在高二完成了立體幾何的學(xué)習(xí)，根據(jù)北京高考的實(shí)際情況，所有學(xué)生都學(xué)習(xí)了空間幾何體、空間點(diǎn)線面的位置關(guān)系以及利用空間向量解決立體幾何的問(wèn)題.到了高三，師生們更多地關(guān)注了利用空間向量解決問(wèn)題，而忽略了對(duì)學(xué)生空間想象能力的進(jìn)一步培養(yǎng).但是很多研究表明，學(xué)習(xí)立體幾何應(yīng)重在培養(yǎng)學(xué)生的空間想象能力，所以，在高三立體幾何的復(fù)習(xí)過(guò)程中，還是要關(guān)注學(xué)生對(duì)于圖形的再認(rèn)識(shí)，對(duì)于點(diǎn)線面關(guān)系的綜合認(rèn)識(shí)，而后再利用空間向量作為工具來(lái)驗(yàn)證結(jié)論，通過(guò)“實(shí)踐—反思—提煉—再實(shí)踐”的學(xué)習(xí)方式，利用APOS引導(dǎo)學(xué)生進(jìn)行有效的學(xué)習(xí)，提高學(xué)生的直觀想象和邏輯推理能力.

2 “活動(dòng)（Action）階段”一一建構(gòu)直觀想象能力的起點(diǎn)

APOS理論的活動(dòng)階段是指教師根據(jù)學(xué)生已有的知識(shí)經(jīng)驗(yàn)，合理地為學(xué)生提供感性素材，刺激他們的視覺(jué)和聽(tīng)覺(jué)，并對(duì)其進(jìn)行感知和轉(zhuǎn)換，在這里，“活動(dòng)”不僅包括可看見(jiàn)的行為，還包括一些隱性的、能激發(fā)學(xué)生思維的活動(dòng).

在高三立體幾何的復(fù)習(xí)過(guò)程中，讓學(xué)生再一次重現(xiàn)認(rèn)識(shí)的基本圖形，在圖形中發(fā)現(xiàn)并應(yīng)用空間幾何體點(diǎn)線面的位置關(guān)系或者空間向量來(lái)驗(yàn)證結(jié)論，這個(gè)過(guò)程就是抽象思維的操作過(guò)程.

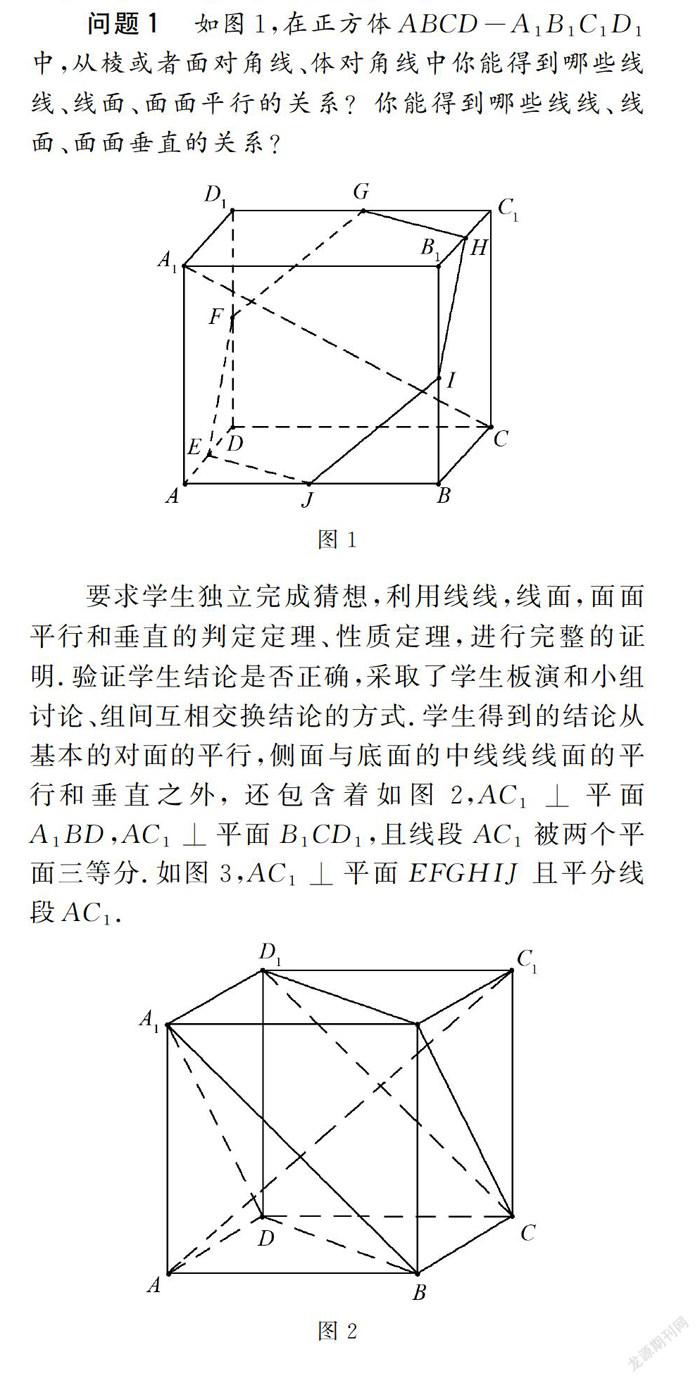
問(wèn)題1 如圖1，在正方體ABCD-A1B1C1D1中，從棱或者面對(duì)角線、體對(duì)角線中你能得到哪些線線、線面、面面平行的關(guān)系？你能得到哪些線線、線面、面面垂直的關(guān)系？

要求學(xué)生獨(dú)立完成猜想，利用線線，線面，面面平行和垂直的判定定理、性質(zhì)定理，進(jìn)行完整的證明.驗(yàn)證學(xué)生結(jié)論是否正確，采取了學(xué)生板演和小組討論、組間互相交換結(jié)論的方式.學(xué)生得到的結(jié)論從基本的對(duì)面的平行，側(cè)面與底面的中線線線面的平行和垂直之外，還包含著如圖2，AC1⊥平面A1BD，AC1⊥平面B1CD1，且線段AC1被兩個(gè)平面三等分.如圖3，AC1⊥平面EFGHIJ且平分線段AC1.

問(wèn)題的設(shè)計(jì)，使學(xué)生在“活動(dòng)”階段感知到了線線線面的平行和垂直，從而將學(xué)過(guò)的定理定義再現(xiàn)，并且進(jìn)行互相轉(zhuǎn)化證明直觀感知到的結(jié)論.通過(guò)感知和證明的過(guò)程使學(xué)生把接觸到的數(shù)學(xué)對(duì)象通過(guò)一步步的外顯性操作指令進(jìn)行轉(zhuǎn)換，這樣有助于學(xué)生加深對(duì)立體幾何整體性的把握.

3 “過(guò)程（Process）階段”一一對(duì)于直觀感知的反思和總結(jié)

APOS理論的“過(guò)程階段”指的是同學(xué)們?cè)谡鎸?shí)的操作中會(huì)初步、直觀地感知概念，這能讓他們?nèi)计饘W(xué)習(xí)的熱情，他們會(huì)有強(qiáng)烈的學(xué)習(xí)動(dòng)機(jī).過(guò)程階段也是整理、分析、處理感性材料的階段，在這個(gè)階段中，學(xué)生會(huì)經(jīng)歷聯(lián)想、想象、觀察等過(guò)程，會(huì)對(duì)所學(xué)的知識(shí)進(jìn)行思考、總結(jié)、分析，將知識(shí)內(nèi)化.這需要學(xué)生展示思考的過(guò)程，才能實(shí)現(xiàn)對(duì)問(wèn)題的總體認(rèn)識(shí)和反思.

問(wèn)題2 如圖4，在正方體ABCD-A1B1C1D1中，點(diǎn)E是棱CC1上的一個(gè)動(dòng)點(diǎn)，平面BED1交棱AA1于點(diǎn)F.則下列命題中假命題是（? ）

（A）存在點(diǎn)E，使得A1C1//平面BED1F.

（B）存在點(diǎn)E，使得B1D⊥平面BED1F.

（C）對(duì)于任意的點(diǎn)E，平面A1C1D⊥平面BED1F.

（D）對(duì)于任意的點(diǎn)E，四棱錐B1-BED1F的體積均不變.

對(duì)于問(wèn)題2，利用問(wèn)題1的結(jié)論，可以很快判斷出A，C，D是正確的，但是要求學(xué)生寫出嚴(yán)格的證明.尤其對(duì)于選項(xiàng)B，可以利用反證法，假設(shè)B1D⊥平面BED1F，從而推導(dǎo)出B1D⊥BD1而與題目的條件產(chǎn)生了矛盾.

問(wèn)題3 如圖5，在正方體ABCD-A1B1C1D1中，若點(diǎn)P（異于點(diǎn)B）是棱上一點(diǎn)，則滿足BP與AC1所成的角為45°的點(diǎn)P的個(gè)數(shù)為

對(duì)于問(wèn)題3，方法1：利用問(wèn)題1結(jié)論構(gòu)造各棱頂點(diǎn)與直線AC1所成的角與450相比較，可以發(fā)現(xiàn)只有B1C1，C1C，C1D1上存在點(diǎn)P.方法2：應(yīng)用空間向量設(shè)出點(diǎn)P在各個(gè)棱上的點(diǎn)坐標(biāo)，利用兩條直線所成角，確定點(diǎn)P的位置.方法3：延長(zhǎng)D1A1到點(diǎn)E，使得

D1A1=A1E，由此BE//CA1，所以，點(diǎn)P的軌跡在以點(diǎn)B為頂點(diǎn)，BE為軸頂角為π2的圓錐底面上.通過(guò)觀察圖形，可以發(fā)現(xiàn)圓錐只與B1C1，C1C，C1D1相交，故存在點(diǎn)P.

類似利用問(wèn)題1的一些結(jié)論，可以快速的解決正方體中的一些結(jié)論，解決問(wèn)題的“過(guò)程階段”是學(xué)生對(duì)問(wèn)題1的操作活動(dòng)進(jìn)行反思和總結(jié)，通過(guò)觀察圖形、遷移到相似圖形、進(jìn)行判斷，證明和總結(jié)等過(guò)程，對(duì)于立體幾何的知識(shí)內(nèi)容不斷內(nèi)化和壓縮，抽象解決立體幾何的基本方法.

4 “對(duì)象（Object）階段”一一學(xué)習(xí)的整合階段

APOS理論的“對(duì)象階段”是經(jīng)過(guò)上面兩個(gè)階段的學(xué)習(xí)后，學(xué)生能夠在學(xué)習(xí)中形成整體思維，會(huì)獨(dú)立思考問(wèn)題，成為相對(duì)獨(dú)立的個(gè)性，會(huì)運(yùn)用整合、歸納、分析等思維讓兩個(gè)概念之間產(chǎn)生聯(lián)系但又相互獨(dú)立.[4]在學(xué)習(xí)立體幾何時(shí)，學(xué)生要對(duì)研究的立體幾何對(duì)象進(jìn)行直觀感知之后的自然語(yǔ)言、圖形語(yǔ)言、符號(hào)語(yǔ)言之間的相互轉(zhuǎn)換.

問(wèn)題4 如圖6，四棱錐P-ABCD中，AB∥CD，AB=2CD，E為PB的中點(diǎn).

求證：CE//平面PAD

問(wèn)題4的解決是在前兩個(gè)階段的學(xué)習(xí)之上，讓學(xué)生熟練靈活應(yīng)用立體幾何的知識(shí)來(lái)解決問(wèn)題.但是在這個(gè)過(guò)程中要揭示線面平行本質(zhì)，是要找尋平面PAD內(nèi)的一條直線與CE平行，這條直線是過(guò)CE的平面與平面PAD的交線.這就涉及到了平面確定的問(wèn)題，不共線的三點(diǎn)確定一個(gè)平面，兩條平行線確定一個(gè)平面.在圖6上我們可以發(fā)現(xiàn)直線DF與直線CE構(gòu)成了一個(gè)平行四邊形，確定了一個(gè)平面，DF就是我們所尋找的交線.同理，在直線AB上任取一點(diǎn)G，點(diǎn)G在平面PAB和平面ABCD的交線上，由此EG與AP交于點(diǎn)K，CG與AD交于點(diǎn)H，HK是平面ECG與平面PAD的交線.通過(guò)引導(dǎo)學(xué)生確定平面，可以在平面PAD找到很多條符合條件的直線.在這個(gè)分析，總結(jié)，歸納過(guò)程中，既讓學(xué)生應(yīng)用了立體幾何的基本知識(shí)，也給學(xué)生建立了如何解決問(wèn)題的基本思路，培養(yǎng)了學(xué)生邏輯推理素養(yǎng).在這基礎(chǔ)之上，繼續(xù)追問(wèn)學(xué)生平面PAB與平面PCD的交線在哪里？與直線AD是什么位置關(guān)系？學(xué)生既可以利用剛剛應(yīng)用的線線平行，線面平行的定理，也可以發(fā)現(xiàn)點(diǎn)P可以看成正方體ABCD-A1B1C1D1中，平面A1B1C1D1上任意一點(diǎn)，如圖7，會(huì)很快找到交線的位置.當(dāng)然還可以繼續(xù)在正方體中進(jìn)行割補(bǔ)找尋更多的位置關(guān)系.

以問(wèn)題4為例，對(duì)象階段學(xué)生已經(jīng)不需要進(jìn)行對(duì)具體問(wèn)題過(guò)程的步驟進(jìn)行具體分析了，而是將研究問(wèn)題的整個(gè)“過(guò)程”看作一個(gè)整體，把在“過(guò)程階段”得出的立體幾何的線線、線面、面面平行結(jié)論進(jìn)行分析和抽象，從而幫助學(xué)生體會(huì)立體幾何平行問(wèn)題的本質(zhì)，和學(xué)生共同討論和總結(jié)平行問(wèn)題的解決方法，給出具體的明確的解決方案，才能形成完整的對(duì)象階段.所以，對(duì)象階段強(qiáng)調(diào)的是學(xué)生對(duì)一類問(wèn)題的理解和總結(jié)并形成具體方案.從“過(guò)程階段”過(guò)渡到“對(duì)象階段”是需要學(xué)生從對(duì)具體的每一個(gè)問(wèn)題的反思，總結(jié)，將這類問(wèn)題進(jìn)行歸納，建構(gòu)系統(tǒng)的過(guò)程由過(guò)程，需要在教師的指導(dǎo)下，學(xué)生需要進(jìn)行不斷地反思、總結(jié)，抽象，的過(guò)程.對(duì)于立體幾何中垂直關(guān)系的教學(xué)也可以這樣完成.

5 結(jié)語(yǔ)

總之，數(shù)學(xué)的學(xué)習(xí)是需要經(jīng)歷“實(shí)踐—反思—提煉—再實(shí)踐”的過(guò)程的，這個(gè)過(guò)程與APOS理論的四個(gè)過(guò)程相吻合，所以在數(shù)學(xué)教學(xué)上應(yīng)用APOS理論，使學(xué)生在學(xué)習(xí)中經(jīng)歷螺旋式的建構(gòu)過(guò)程，對(duì)于學(xué)生的數(shù)學(xué)素養(yǎng)的形成有一定的幫助.在今后的實(shí)踐中，筆者會(huì)繼續(xù)反思和優(yōu)化APOS理論的四個(gè)過(guò)程，使教學(xué)過(guò)程取得更好的效果.

參考文獻(xiàn)：

[1]Dubinsky，E.Teaching Mathematical Inductio I[J].Journal of Mathematical? Behavior，1997（16）：187-239.

[2]喬連全.APOS理論是一種建構(gòu)主義[J].全球教育展望，2001 （3）：16-20.

[3]褚艷春.如何在立體幾何中用好空間向量[J].學(xué)周刊，2011（11）.

[4]唐毽香.基于APOS理論的高中立體幾何概念教學(xué)研究[D].湖南師范大學(xué).2016

[5]郭芳APOS理論下立體幾何線面位置關(guān)系的教學(xué)研究[D].河南大學(xué). 2019