三維集成電路中基于多棱柱單元有限元法的寄生參數提取

張 程，徐小宇，任卓翔

（1.中國科學院微電子研究所，北京 100029；2.中國科學院大學，北京 100049；3.索邦大學，巴黎75006）

集成電路加工工藝已經進入跨越3 nm 的時代，新結構、新材料的應用以及工藝漲落對于電路性能的影響也更加顯著，也對互聯寄生參數的提取提出了更高的要求。參數提取主要依賴麥克斯韋方程組的電磁場求解器，其中，廣泛采用的方法是有限元法（FEM）[1-6]。總的來說，有限元法將節點標量電勢、棱邊矢量電位等作為未知量，對于網格，采用插值規則建立代數方程組，其中網格單元可以是不同幾何形狀[1-7]。所有有限元求解器的作用都針對的是性能提升，并在效率與精度之間進行權衡。近些年來，有限元法的能量互補和對偶性被廣泛研究，該特性被用來加速求解收斂[3-4]。所謂的對偶有限元法，即節點有限元和棱邊有限元，分別將原始網格上節點標量電位和棱邊上的矢量電位作為未知量。電容參數提取是一類靜電場問題，采用矢量電位時會出現多值問題，可通過在帶電荷區域和多連通域之間建立“連接”來解決[1]。根據歐拉特性，棱邊有限元總是會導致出現更多的自由度，因此在對偶網格上采用標量電勢作為未知量，可以提供FEM 的另一種解決方案如下。

對偶網格由多邊形（二維）及多面體（三維）單元組成，廣義重心坐標系（GBCs）可被用來為這些單元提供近似插值函數[7-8]。基于GBCs的伽遼金格式的有限元可稱為多邊形或多面體有限元。近些年來，基于GBCs的有限元法獲得了較多的關注并顯示出新的前景[9-13]，且在計算機圖形學、拓撲優化[14-15]、力學[9]、熱學和電磁學[1,8]等領域已經有許多研究，然而該算法的高復雜度和耗時阻礙了應用推廣。為了在三維對偶網格上更加有效地建立變量有限元，文中提出了一種在多棱柱單元上分片插值的方法，并通過算例給出三維電容參數提取結果的收斂性和精確性。

1 原始網格及對偶網格

給定一個Delaunay三角化網格，很容易獲得它的關聯對偶網格，分別稱為原始網格MP及對偶網格MD，如圖1 所示。通常情況下，采用基于外心的方式從原始網格獲得對偶網格，此時兩套網格互相正交。

圖1 網格的二維及三維視圖

雖然已有PolyMesher 等工具可用來生成多邊形網格[16]，但為了從已建立的原始網格中產生對偶網格，應當注意不同區域的交界面。如圖2 所示，由于界面的存在，多邊形c3、c2被分割為若干個部分。尤其是MP中形態不佳的三角形會導致多邊形c2和c5也處于形態不佳的情況，這時可以局部采用重心來構建對偶網格。

圖2 網格以及區域界面

2 廣義重心坐標系及插值

2.1 廣義重心坐標系定義

有限元法中經常采用的重心坐標系僅適用于三角形、四面體等單純形，對于更加廣泛的多邊形與多面體，廣義重心坐標系（GBCs）可視為重心坐標在多邊形和多面體上的延伸。GBCs 函數λi在多邊形或多面體Ω內的某個點vi滿足非負性、線性完備性、單位性、克羅內克函數特性等性質[1,8]。

GBCs 滿足作為代數基的伽遼金逼近函數的充分必要條件，也有大量GBCs 可供選擇。在FEM 框架下，需要計算λ與gradλ，并且對gradλ及gradλi、gradλj在單元上進行積分。對于GBCs 而言，該計算非常耗時，可以考慮采用近似插值技術。

2.2 分片插值廣義重心坐標系

考慮到在三棱柱上的能量積分相對容易，可以考慮選取一個點將具有n條邊的凸多棱柱分為多個三棱柱，其中電場和能量可以分開計算。這種分片插值算法可用來簡化GBCs 和其梯度計算，并可以用于FEM 計算。

2.2.1 選取插值點

為了準確地表達多棱柱各節點之間的關聯關系，首先需要定位插值點，根據經驗可知，多胞體的重心或最大內切球的球心是較好的選擇。考慮到可能會存在多個最大內切球，所以選擇其中最靠近重心的球心。為簡便起見，文中采用重心作為插值點，如圖3（a）中的do，n邊多棱柱可分為n個三棱柱，其中，do(1)與do(2)分別是do在頂面與底面上的投影，包含了do的橫截面如圖3（b）所示。設定凸多邊形d1…dn的第i個頂點坐標為(xi,yi,zi)。

圖3 多棱柱單元及其橫截面圖

2.2.2 確定插值點上的標量電勢

一旦給出了插值點，施加在該點上的電勢值即可被確定。一般采用能量最小原則來確定插值點上的標量電勢。

如圖3（a）所示，設多棱柱上的節點上的電勢為，其中r=1,…,n；s=1,2。假定重心do上的待定電勢為vo，每個子區域中的能量可根據公式計算得出，累加所有子區域的能量，就可以得到多棱柱單元的總能量We。

顯然，We是vo的函數，可通過局部極值點的計算來查找vo以使局部能量最小化，也就是尋求對該點電勢的偏導數為零的能量：

根據計算得到電勢為：

其中，權重系數γi可表示為：

可以證明權重系數在每個單元內的和為1，即滿足單元性。并且也可以得到：

因此，基于式（2）獲得的值是最小值。

2.2.3 形函數

如圖3（a）所示，考察落入子區域dodidi+1的d*點上的電勢，可以推出單元dodidi+1上的形函數N(s)為：

其中，s取值1、2，分別表示上、下表面，且有：

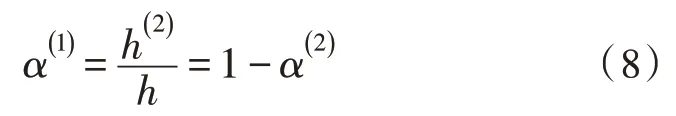
關于棱柱單元d1...dn之中電勢的連續性，根據式（5）～（7）可以看出，在插值點、頂點及連線上是0階連續，在所有棱、面上是1 階連續，在其他地方是無窮階連續。

2.2.4 單元及總體剛度矩陣

根據局部區域能量最小的原理以及式（5）～（7），對于計算區域Ω上的偏微分方程問題，可以很容易得到n邊多棱柱單元的系數矩陣元素。

這樣就建立起了單元和總體剛度矩陣。最后，求解所得到稀疏矩陣，即可得到每一個節點上的標量電勢。

3 數值分析算例

寄生參數提取是集成電路工業中的重要議題，它是典型的靜電場問題。文中利用所提出的有限元法在對偶網格MD中提取8 導體結構的電容值。如圖4 所示，C8被設為主導體并施加1 V 電壓，其他導體作為環境導體并施加0 V 電壓。

圖4 三維多導體系統的電容參數提取算例結構示意圖

圖4 中描述的是8 導體結構，導體被相對介電常數為3.70 的材料（圖中所示的尺寸非等比例）包圍。

如圖5 所示，計算區域經Delaunay 三角化離散形成原始網格MP，然后通過外心形成對偶網格MD。文中采用了標量的原始有限元（primal FEM，標記為pFEM）、矢量對偶有限元（dual FEM，標記為dFEM），以及所提出的多胞體（如多棱柱）有限元（polytope FEM，標記為tFEM）。

圖5 網格單元

電勢分布及能量的計算結果如圖6 所示。由于對偶有限元的兩種方法具有能量互補特征，其均值也被用來作為參考基準。針對原始網格上的算例#1 與算例#2，算例#1 具有9 126 個節點、16 150 個單元，算例#2 具有41 834 個節點、77 550 個單元，計算相關概要信息，如表1、表2 所示。對應情況下，指定的主導體C8的自電容與互電容結果如表3、表4 所示。

圖6 不同有限元法計算獲得的電勢分布計算結果

表1 不同算例網格的概要信息

表2 不同算例有限元法計算的概要信息

表3 不同有限元法的算例#1電容參數提取結果

表4 不同有限元法的算例#2電容參數提取結果

隨著網格加密的電容參數提取結果如圖7 所示，結果表明，多胞體有限元法具有良好的收斂性和精度，與原始有限元法相比，雖然耗時略多，但明顯具有更高的精度。

圖7 導體C4與C8之間的電容

4 結論

與基于原始網格的傳統標量有限元法及矢量有限元法不同，文中給出了一種基于對偶網格的標量有限元法，該方法采用廣義重心坐標系進行插值函數的構建。這類方法近些年才重新興起，并在包括電磁場分析的領域有所應用，但是廣義重心坐標及相應的有限元法計算復雜度過高，文中針對三維多棱柱單元，提出一種基于分片插值的方法，以快速獲得伽遼金格式的有限元法的形函數，并將其用于集成電路的參數提取。對數值的分析結果表明，該方法具有良好的精度，且隨著網格的加密也呈現出穩定的收斂性。該方法容易推廣到其他單元類型，并且對偶網格也很容易由原始網格導出。

從經驗上來看，多胞體有限元法比原始網格上的標量有限元法的精度高，該方法實際上隱含了在多個細密的網格上進行形函數導出的過程。為了將多胞體有限元應用于實際工程，有必要對網格離散誤差和有限元計算誤差的估計進行理論研究。