基于水生系統(tǒng)的常微分方程平衡點(diǎn)的定性分析

劉 煦，陳思潼

(1.吉林財(cái)經(jīng)大學(xué)應(yīng)用數(shù)學(xué)學(xué)院，吉林 長春 130117；2.黑龍江大學(xué)數(shù)學(xué)科學(xué)學(xué)院，黑龍江 哈爾濱 150080)

1 預(yù)備知識

藻類是水生生態(tài)系統(tǒng)中的重要初級生產(chǎn)者，可以進(jìn)行光合作用和化學(xué)合成[1].藻類的空間結(jié)構(gòu)一般分為上下兩層，位于上層懸浮于水中的稱為浮游藻類，位于下層生長于水下各種基質(zhì)表面的稱為底棲藻類[2-4].二者共同構(gòu)成了藻類種群的重要初級生產(chǎn)者，是水生動物的重要食物來源之一，是水體物質(zhì)和能量循環(huán)中重要一環(huán).

營養(yǎng)是藻類生長的必備元素之一.淡水湖泊營養(yǎng)豐富的環(huán)境下，因?yàn)樗泻写罅康牧住⒌仍兀罅坑袡C(jī)物在水中降解釋放出營養(yǎng)元素，促進(jìn)水中藻類瘋狂增長.但藻類死后分解出大量有毒物質(zhì)，致使水生生物由于缺氧或中毒而大量死亡，這樣就破壞了整個(gè)淡水湖泊的生態(tài)系統(tǒng)[5].因此，研究藻類和營養(yǎng)的數(shù)學(xué)模型具有重要的實(shí)際應(yīng)用價(jià)值.

近年來，國內(nèi)外許多學(xué)者已經(jīng)建立并研究了藻類和營養(yǎng)的數(shù)學(xué)模型，得到了許多優(yōu)秀的研究成果[2，6-10].本文參考文獻(xiàn)[3]建立了一個(gè)淺水生態(tài)系統(tǒng)中浮游藻類-底棲藻類-營養(yǎng)常微分方程模型：

(1)

其中:U，V分別表示浮游藻類和底棲藻類種群密度；R，W分別是水中浮游層營養(yǎng)和底棲層營養(yǎng)；ru，rv表示種群的內(nèi)稟增長率；mu，mv分別表示種群U和V的死亡率；Rsur是外界營養(yǎng)輸入；Wsed是底層沉淀物釋放出的營養(yǎng)；L1，L2表示水中浮游層和底棲層的水深；a，b，c分別表示浮游層營養(yǎng)和底棲層營養(yǎng)、底泥中營養(yǎng)和底棲層營養(yǎng)、外界營養(yǎng)與浮游層營養(yǎng)之間的交換率；η表示浮游藻類的下沉率；γu，γv是半飽和系數(shù)；cu，cv是藻類的碳磷比；βu，βv表示藻類死亡后的營養(yǎng)釋放率.鑒于模型(1)的實(shí)際生物意義，假設(shè)模型(1)的初始值都是正的，即U(0)>0，V(0)>0，W(0)>0，R(0)>0.

2 平衡點(diǎn)存在性與穩(wěn)定性

研究模型(1)的平衡點(diǎn)的存在性及穩(wěn)定性.模型(1)的平衡點(diǎn)如下：

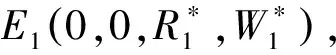
(2)

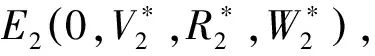
(3)

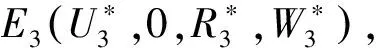
(4)

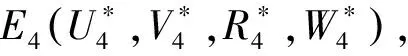
(5)

為了判斷這些平衡點(diǎn)的局部漸近穩(wěn)定性，需要考慮模型(1)的Jacobian矩陣.經(jīng)簡單計(jì)算可得模型(1)的Jacobian矩陣為

其中：

其余元素均為0.

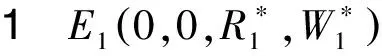
(6)

時(shí)，E1是局部漸近穩(wěn)定的.

證明通過求解方程(2)，可得

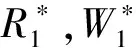
因而當(dāng)(6)式成立時(shí)，有

這說明J(E1)的特征根均具有負(fù)實(shí)部，因此，E1是局部漸近穩(wěn)定的.

定理2 若

(7)

(8)

時(shí)，E2是局部漸近穩(wěn)定的.

證明通過求解方程(3)，可得

注意到

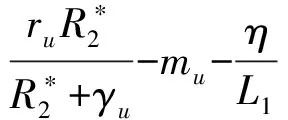
考慮特征多項(xiàng)式

f(λ)=|λI-A|=λ3+A1λ2+A2λ+A3，

其中：

所以，當(dāng)(8)式成立時(shí)，有Ai>0，i=1，2，3，A1A2-A3>0，于是J(E2)的特征根均具有負(fù)實(shí)部.因此，E2是局部漸近穩(wěn)定的.

那個(gè)時(shí)候的我們，不談學(xué)業(yè)，不言前程。不說喜歡，也不言愛情。自自然然，簡簡單單，一袋零食，兩三本書，就可以去到學(xué)校后面的小山坡上坐上半天，說說話，發(fā)發(fā)呆。沒有未來，我們便不談未來。只談《梅花三弄》，只談《七劍下天山》……

定理3 若

則E3存在，并且當(dāng)

(9)

時(shí)，E3是局部漸近穩(wěn)定的.

證明通過解方程(4)，可得

在E3處的Jacobian矩陣為

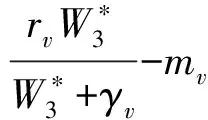
考慮特征多項(xiàng)式

g(λ)=|λI-B|=λ3+B1λ2+B2λ+B3，

其中：

若條件(9)成立，易知

Bi>0，i=1，2，3，B1B2-B3>0，

這說明J(E3)的特征根均具有負(fù)實(shí)部，因此，E3是局部漸近穩(wěn)定的.

定理4 若

(10)

則E4存在且是局部漸近穩(wěn)定的.

證明通過求解方程(5)，可得

若條件成立，則E4存在.直接計(jì)算有

其特征多項(xiàng)式為h(λ)=λ4+C1λ3+C2λ2+C3λ+C4，其中：

易證若(10)式成立，則

因而，J(E4)的特征根均具有負(fù)實(shí)部.于是E4是局部漸近穩(wěn)定的.

3 數(shù)值模擬

取γu=3，γv=5，cu=0.008，cv=0.015，βu=0.5，βv=0.3，ru=1，rv=1，η=0.1，L1=2，L2=0.01，a=0.05，b=0.05，c=0.01，Wsed=0.03，Rsur=0.3.

經(jīng)計(jì)算得模型(1)的平衡點(diǎn)，見圖1.在圖1(a)中，E1是一個(gè)穩(wěn)定的平衡點(diǎn)，意味著U，V種群都滅絕；圖1(b)中，E2是一個(gè)穩(wěn)定的平衡點(diǎn)，表示底棲藻類V滅絕；圖1(c)中，E3是一個(gè)穩(wěn)定的平衡點(diǎn)，表示浮游藻類U滅絕；圖1(d)中E4是一個(gè)穩(wěn)定的平衡點(diǎn)，表示所有種群共存.以mu，mv為參數(shù)，建立了平衡點(diǎn)的分布圖，見圖2，其中：

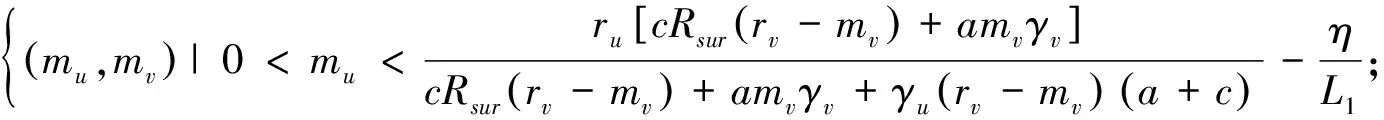
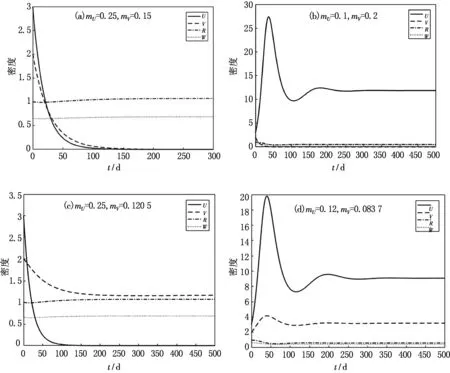
圖1 模型(1)的平衡點(diǎn)

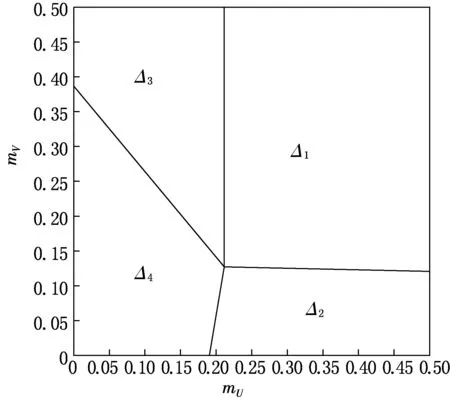
圖2 模型(1)的平衡點(diǎn)分布圖