從復(fù)雜背景下抽象幾何模型研究

福建廈門(mén)雙十中學(xué)思明分校（361000） 康曉靈

下面以一道考試題為例，淺析如何在復(fù)雜背景下抽象出幾何模型。

一、題目呈現(xiàn)

如圖1，在平面直角坐標(biāo)系中，O為坐標(biāo)原點(diǎn)，動(dòng)點(diǎn)P從點(diǎn)A出發(fā)以每秒2個(gè)單位長(zhǎng)度的速度沿線(xiàn)段AO向終點(diǎn)O運(yùn)動(dòng)，同時(shí)動(dòng)點(diǎn)Q從點(diǎn)O出發(fā)以相同速度沿y軸正半軸運(yùn)動(dòng)，當(dāng)點(diǎn)P到達(dá)點(diǎn)O，兩點(diǎn)同時(shí)停止運(yùn)動(dòng)。

圖1

（1）當(dāng)t=______時(shí)，∠OPQ=45°；

（2）如圖2，以PQ為斜邊在第一象限作等腰直角三角形PQM，求點(diǎn)M坐標(biāo)；

圖2

（3）在（2）的條件下，點(diǎn)R為x軸負(fù)半軸上一點(diǎn)，且，點(diǎn)M關(guān)于PQ的對(duì)稱(chēng)點(diǎn)為點(diǎn)N，當(dāng)t為何值時(shí)，△ONR為等腰直角三角形。

二、題目分析

本題是一道在坐標(biāo)系背景下，結(jié)合動(dòng)點(diǎn)的綜合題。八年級(jí)學(xué)生剛剛學(xué)完三角形全等的基本證明，對(duì)于全等三角形的性質(zhì)和判定還不夠熟練，在面對(duì)稍微復(fù)雜的圖形，特別是線(xiàn)條比較多的情況時(shí)，要能根據(jù)題目看出三角形全等的條件或者找到三角形全等的證明思路不太容易。坐標(biāo)系背景下的幾何本身是一個(gè)難點(diǎn)，同時(shí)又加上兩個(gè)運(yùn)動(dòng)的點(diǎn)，更是增加了難度。本題從簡(jiǎn)單到復(fù)雜，設(shè)置了三個(gè)小問(wèn)題，第（1）問(wèn)相對(duì)來(lái)說(shuō)比較容易，從問(wèn)題可以得到OQ=OP，進(jìn)而求出時(shí)間t。第（2）問(wèn)的難度中等，但是大部分學(xué)生拿不到分，原因在于遇到兩個(gè)動(dòng)點(diǎn)P，Q，不知道如何表示，同時(shí)也不知道如何利用含有t的式子來(lái)表示出邊之間的關(guān)系。有部分學(xué)生由已知條件的等腰直角三角形，想要表示出兩條直角邊的長(zhǎng)度，于是利用了還未學(xué)的勾股定理，而這樣不僅增加了計(jì)算量，還算不出來(lái)。出現(xiàn)這種情況的根本原因是學(xué)生無(wú)法抽象出基本圖形，構(gòu)造全等，看到點(diǎn)的坐標(biāo)不能自然想到過(guò)此點(diǎn)作x軸和y軸的垂線(xiàn)段。第（3）問(wèn)，學(xué)生的困惑較大，首先因?yàn)辄c(diǎn)P，Q是運(yùn)動(dòng)的，位置無(wú)法確定；其次點(diǎn)M關(guān)于PQ的對(duì)稱(chēng)點(diǎn)比較抽象，故不容易根據(jù)題意直接畫(huà)出圖形；最后因?yàn)樯婕暗妊苯侨切危⑽粗苯痈嬷苯呛椭苯沁叄孕枰M(jìn)行分類(lèi)討論。本題對(duì)學(xué)生的抽象思維能力要求較高，是一道綜合性題目。

三、學(xué)情分析

八年級(jí)學(xué)生已經(jīng)學(xué)習(xí)了基本的幾何圖形——線(xiàn)段和角，同時(shí)也學(xué)習(xí)了三角形和平行四邊形，從一般到特殊的研究思路讓他們更深刻地理解研究幾何的各要素之間的關(guān)系。因此，學(xué)生對(duì)探究的方向和探究的方法有一定的思考。但是很多學(xué)生對(duì)于動(dòng)點(diǎn)問(wèn)題比較畏懼，往往看到題目會(huì)比較慌張，從而影響審題，再加上是四邊形的背景，尤其是特殊四邊形的性質(zhì)或者三角形全等的條件不易被發(fā)現(xiàn)時(shí)，動(dòng)點(diǎn)放在平面直角坐標(biāo)系中，學(xué)生不容易看出，所以增加了解題難度。目前學(xué)生接觸得比較多的是數(shù)軸上的動(dòng)點(diǎn)問(wèn)題，而且基本是設(shè)置一個(gè)動(dòng)點(diǎn)。學(xué)生在理解動(dòng)點(diǎn)的運(yùn)動(dòng)方向、運(yùn)動(dòng)速度、運(yùn)動(dòng)的路程時(shí)，用含有參數(shù)的式子表示距離沒(méi)有問(wèn)題，但是對(duì)于兩個(gè)動(dòng)點(diǎn)的相對(duì)關(guān)系的尋找或者等量關(guān)系的尋找會(huì)存在一定的困難，這也是本題為什么要先做一個(gè)鋪墊的原因。一方面讓學(xué)生明確從簡(jiǎn)單到復(fù)雜的思考方向，增強(qiáng)探索欲和學(xué)習(xí)信心；另一方面為后面研究更復(fù)雜的問(wèn)題做好準(zhǔn)備，一步步引導(dǎo)學(xué)生探究，并抽象出基本圖形，同時(shí)還作為一種方法，遷移應(yīng)用到后續(xù)的更復(fù)雜的四邊形和圓等幾何圖形的研究中。

四、解法探究

（1）特殊情況。如圖3，當(dāng)∠OPQ=45°時(shí)，學(xué)生不難發(fā)現(xiàn)，此時(shí)△OPQ為等腰直角三角形，所以O(shè)P=OQ，那么問(wèn)題轉(zhuǎn)化為根據(jù)OP=OQ求t的問(wèn)題。因此，需要先用含有t的式子表示出OP和OQ，而速度已知，時(shí)間為t，自然得出OQ=2t，AP=2t，所以O(shè)P=8-2t，因此由OP=OQ這個(gè)等量關(guān)系可以列出方程：8-2t=2t，所以t=2。

圖3

（2）如圖4，已知等腰直角△PQM，易得MQ=MP，∠QMP=90°，從點(diǎn)M的坐標(biāo)入手，必須確定點(diǎn)M到x軸和y軸的距離，方能求出坐標(biāo)，向x軸和y軸作垂線(xiàn)段，只要輔助線(xiàn)一旦作出來(lái)，那么問(wèn)題就迎刃而解了。不難證出△MBQ≌△MCP，因而得到MB=MC，BQ=CP。設(shè)運(yùn)動(dòng)時(shí)間為t，則AP=2t，OQ=2t，OP=8-2t，則由MB=MC和點(diǎn)M在第一象限，可以引入?yún)?shù)，設(shè)M(x,x)，因此OC=OB=x，所以CP=OP-OC=8-2t-x，BQ=OB-OQ=x-2t，又因?yàn)锽Q=CP，所以8-2t-x=x-2t，此時(shí)x=4，t剛好消掉，第（2）問(wèn)也就解決了。

圖4

其實(shí)本題是一個(gè)等腰直角三角形的旋轉(zhuǎn)或“一線(xiàn)三等角”的幾何基本模型，學(xué)生若能大膽猜想，大膽畫(huà)輔助線(xiàn)，大膽設(shè)元，就能夠更快地找到解題突破口。

（3）此問(wèn)是在第（2）問(wèn)的條件下，那么第（2）問(wèn)的條件是什么？第（2）問(wèn)的條件是△PQR是以PQ為斜邊的等腰直角三角形，并且求出了點(diǎn)M的坐標(biāo)為（4，4），這些條件可以使用，接下去給出的條件是由（2）可知OP=8-2t，所以O(shè)R=4-t，而最后一個(gè)條件是點(diǎn)M關(guān)于PQ的對(duì)稱(chēng)點(diǎn)為點(diǎn)N，這是本題的棘手處，學(xué)生無(wú)法直觀想象出一個(gè)定點(diǎn)關(guān)于兩個(gè)動(dòng)點(diǎn)所連的線(xiàn)段軸對(duì)稱(chēng)的點(diǎn)的位置，同時(shí)也無(wú)法求出來(lái)，并且不好畫(huà)出來(lái)，無(wú)法定出點(diǎn)N的位置，這樣就無(wú)法討論△ONR為等腰直角三角形的可能。因此，本題最需解決的問(wèn)題就是如何確定點(diǎn)N的位置。正因?yàn)槭窃谧鴺?biāo)系背景下，所以很多學(xué)生很想準(zhǔn)確地畫(huà)出坐標(biāo)系，并且嘗試在各種P，Q位置作出對(duì)稱(chēng)，還去討論P(yáng)，Q，N在各個(gè)象限或坐標(biāo)軸中運(yùn)動(dòng)的可能性，而且畫(huà)出的圖形中線(xiàn)段非常多，其實(shí)這是一種誤導(dǎo)，也是一種復(fù)雜的過(guò)程。如果把坐標(biāo)系背景去掉，只是單純地根據(jù)題意畫(huà)出對(duì)稱(chēng)圖，可能圖形就更為簡(jiǎn)單，對(duì)于觀察模型、抽象模型也有幫助。

去掉坐標(biāo)系背景，如圖5所示不考慮點(diǎn)的坐標(biāo)，不難發(fā)現(xiàn)等腰直角△QMP關(guān)于PQ對(duì)稱(chēng)的△QNP同樣也是一個(gè)等腰直角三角形，那么隨著P，Q的變化，點(diǎn)M是固定的，點(diǎn)N的位置肯定會(huì)變化，可能在第四象限或第二象限，在嘗試作圖的過(guò)程中，不難排除第四象限，而第（2）問(wèn)的圖形可以作為一個(gè)啟發(fā)，可以求出運(yùn)動(dòng)時(shí)間t的取值范圍，此時(shí)構(gòu)成的是一個(gè)鈍角三角形，并不是直角三角形，從而縮小求解范圍。解決動(dòng)點(diǎn)問(wèn)題的關(guān)鍵是明白動(dòng)中有不變。在本題中，點(diǎn)R雖然在動(dòng)，但始終在x軸（即射線(xiàn)PO）上運(yùn)動(dòng)，所以畫(huà)圖又縮小了范圍。最后的任務(wù)就是對(duì)等腰直角三角形的頂角和底角、直角邊和斜邊進(jìn)行分類(lèi)。

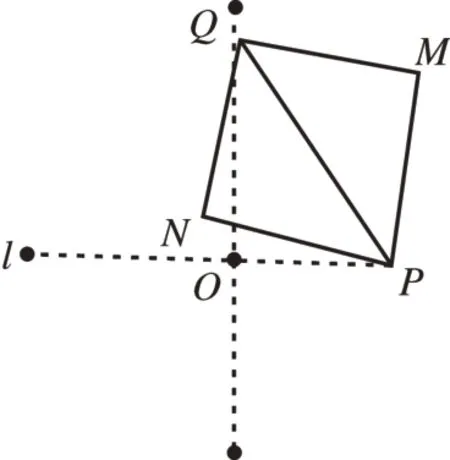
圖5

①當(dāng)AP＜4 時(shí)，即2t＜4，t＜2 時(shí)，此時(shí)點(diǎn)M關(guān)于PQ的對(duì)稱(chēng)點(diǎn)N在第四象限，而點(diǎn)R在x軸負(fù)半軸，此時(shí)△ORN為鈍角三角形，不符合題意。

②當(dāng)t＞2 時(shí)，此時(shí)點(diǎn)N在第二象限，點(diǎn)R在x軸負(fù)半軸上。

（Ⅰ）若∠ONR=90°，RN=ON，如圖6，易得到“一線(xiàn)三等角”的基本模型，△NSP≌△PTM，從而NS=PT，SP=MT。根據(jù)M(4,4)，OP=8-2t，OR=4-t，得出OP=4-(8-2t)=2t-4，所以，解得此時(shí)符合t＞2。

圖6

（Ⅱ）若∠ORN=90°，NR=OR，如圖7，比第（Ⅰ）種情況更為簡(jiǎn)單，更易得出結(jié)果，少作一條輔助線(xiàn)。證明△NRP≌△PTM，從而對(duì)應(yīng)邊NR=OR=4-t，PT=2t-4，根據(jù)NR=PT，得到4-t=2t-4，解得此時(shí)也符合t＞2。

圖7

（Ⅲ）若∠NOR=90°，ON=OR=4-t時(shí)，此時(shí)O，N，Q三點(diǎn)均在y軸上，不滿(mǎn)足∠QNP=90°，因此不能形成等腰直角三角形。

通過(guò)本題的解法探究，筆者得到啟發(fā)，對(duì)于坐標(biāo)系背景下的幾何綜合題，如果題目中的幾何線(xiàn)段比較多、比較復(fù)雜，且點(diǎn)的坐標(biāo)不太受題目條件影響或者能用參數(shù)把運(yùn)動(dòng)變化的點(diǎn)表示出來(lái)，則可嘗試隱去容易干擾的坐標(biāo)系背景，抽象出與所要研究的要素有關(guān)的基本圖形。特別是在后續(xù)的函數(shù)建模中，面對(duì)復(fù)雜的圖形背景，例如拱橋問(wèn)題，學(xué)生如果能隱去無(wú)關(guān)的線(xiàn)段或角，留下需要求的或需要用的線(xiàn)段進(jìn)行函數(shù)的建模，就能較快地求出解析式。通過(guò)本題的深入分析，學(xué)生學(xué)會(huì)隱去無(wú)關(guān)條件，抽象出復(fù)雜背景下的簡(jiǎn)單圖形和基本模型，這對(duì)后續(xù)的幾何學(xué)習(xí)或者函數(shù)建模等起到重要作用。

筆者在進(jìn)行二次函數(shù)的動(dòng)點(diǎn)含參問(wèn)題的教學(xué)中發(fā)現(xiàn)，對(duì)于拋物線(xiàn)上動(dòng)點(diǎn)軌跡的尋找，點(diǎn)的運(yùn)動(dòng)特點(diǎn)是難點(diǎn)，但是當(dāng)將這一難點(diǎn)進(jìn)行拆分，畫(huà)出基本圖形，分解題目條件，尋找與所要求的結(jié)論相關(guān)的線(xiàn)段，聯(lián)想已經(jīng)學(xué)過(guò)的基本全等模型，或者基本等腰三角形、特殊四邊形等，就很容易找到突破口。因此，學(xué)會(huì)在復(fù)雜背景下抽象出簡(jiǎn)單圖形和基本的幾何模型，對(duì)學(xué)生而言非常重要。對(duì)教師而言，如何引導(dǎo)學(xué)生去尋找、去抽象幾何模型是教學(xué)難點(diǎn)，也是需不斷探索的教學(xué)方向。

五、教學(xué)反思

對(duì)于含有復(fù)雜背景的幾何問(wèn)題，尤其是動(dòng)點(diǎn)問(wèn)題，教師應(yīng)引導(dǎo)學(xué)生審清題意，并且根據(jù)命題者所設(shè)計(jì)的幾個(gè)小問(wèn)題串形成自己的思維鏈，從復(fù)雜的背景中抽象出平時(shí)所用到的幾何模型。筆者在近幾年的教學(xué)中發(fā)現(xiàn)，很多學(xué)生在遇到文字?jǐn)⑹鲚^長(zhǎng)的題目時(shí)往往沒(méi)有耐心去認(rèn)真閱讀，對(duì)此教師要引導(dǎo)學(xué)生認(rèn)真讀題，標(biāo)注關(guān)鍵詞，厘清數(shù)量關(guān)系。在當(dāng)前“雙減”的大環(huán)境下，考試的靈活性越來(lái)越大，對(duì)學(xué)生的要求也越來(lái)越高，教師不能僅僅通過(guò)大量刷題來(lái)提升學(xué)生的學(xué)習(xí)能力。近年來(lái)的中考命題和實(shí)際生活聯(lián)系緊密，尤其是應(yīng)用題的背景越來(lái)越生活化，也正是因?yàn)樯罨谋尘埃庞懈嗟奈淖珠喿x量，十分考驗(yàn)學(xué)生的耐心。在平時(shí)教學(xué)中，教師要多培養(yǎng)學(xué)生讀題、審題的良好習(xí)慣。好的解題思路來(lái)源于已有的知識(shí)和經(jīng)驗(yàn)，因此，教師還應(yīng)該滲透綜合分析法，引導(dǎo)學(xué)生通過(guò)適當(dāng)添加輔助線(xiàn)，發(fā)現(xiàn)熟悉的基本圖形，同時(shí)讓學(xué)生自己學(xué)會(huì)總結(jié)、歸納。這樣，學(xué)生對(duì)幾何模型的掌握就會(huì)更加牢固。教會(huì)學(xué)生抽象圖形，特別是從復(fù)雜背景中抽象出幾何模型，將問(wèn)題由繁化簡(jiǎn)，學(xué)生解題思路的生成就會(huì)更加自然。