非厄米鑲嵌型二聚化晶格*

侯博 曾琦波

(首都師范大學物理系，北京 100048)

1 引言

非厄米系統在過去二三十年中引起了研究人員的廣泛關注[1-5].在所研究的系統中，如果要進一步考慮系統與外部環境的相互作用或者影響，可以在系統的哈密頓量中引入非厄米項，如物理增益或者損耗等.非厄米哈密頓量在光學、冷原子系統等經典和量子系統中均有廣泛應用[6-25].不同于傳統的厄米系統中系統能量始終為實數，非厄米系統的能量往往是復數.復數能譜在復能量平面中能表現出更為豐富的能帶結構特征，如點能隙(point gap)和線能隙(line gap)[26]、環狀能隙(loop gap)[27，28]等.如果系統哈密頓量具有PT 對稱性[29-31]或者贗厄米性[32-35]，其能譜也可以為實數.

近年來，具有非對稱躍遷的非厄米系統掀起了新一輪的研究熱潮[36-38].在格點模型中，非對稱躍遷是指相同的兩個格點之間的躍遷在不同方向具有不同的強度.例如，在一維Hanato-Nelson (HN)模型中[39]，粒子向前躍遷與向后躍遷的躍遷振幅不同，從而導致系統的哈密頓量不再是厄米的.具有非對稱躍遷的系統中往往存在非厄米趨膚效應(non-Hermitian skin effect)，即在開邊界條件下，系統的本征態不再分布于整個系統中，而是被局域在系統的邊界上[40，41].由于非厄米趨膚效應的存在，這類系統的能譜對于邊界條件的變化十分敏感[42]，從而為設計新型的傳感器件提供了新的思路和靈感[43-45].此外，非厄米趨膚效應對拓撲態也有重要影響，會破壞傳統的厄米拓撲系統中的體-邊界對應原理[40，41]，這一效應也使得非厄米拓撲系統在最近幾年中得到了深入的研究[45-52].近期的研究表明，非厄米趨膚的拓撲起源為系統在周期邊界條件下存在的點狀能譜[53，54].另一方面，非對稱躍遷對無序或準周期系統中的安德森局域化現象(Anderson localization)也有重要影響[39，55]，其存在往往會引起退局域化效應(delocalization effect)[26，56-59].

目前為止，有關非對稱躍遷的系統的研究主要集中在將非對稱躍遷施加在所有的躍遷項上.最近，研究人員提出了鑲嵌型晶格模型，發現在將周期調制等間距地施加在某些格點上，系統中會出現遷移率邊等有趣的現象[60].類似地，當調制項等間距地施加到躍遷項中時，系統的拓撲態和局域化等也會受到影響[61，62].

本文研究一維非厄米鑲嵌型二聚化晶格模型.在這類系統中，交替變化的非對稱躍遷被等間距地施加在躍遷項中.計算結果表明，在躍遷項均為實數的情形下，系統的能譜可以在一定的參數范圍內保持為實數.隨著非對稱躍遷強度的增大，系統在開邊界條件下的能譜會從實數變為復數.此外，系統的能譜性質和非厄米趨膚效應會受到鑲嵌型調制周期的影響.本文進一步研究了這類系統中的拓撲零能邊界態并在非布洛赫能帶理論的基礎上，計算了貝里相位對其進行表征.本研究工作引入了一類新型的非厄米格點模型，進一步揭示了非厄米系統的新奇特性.

2 非厄米鑲嵌型二聚化晶格模型

2.1 模型哈密頓量

考慮具有最近鄰躍遷的一維格點模型，其中非對稱躍遷被等距離的施加在某些相鄰格點的躍遷項中，如圖1 所示.系統的哈密頓量如下:

圖1 具有鑲嵌型非對稱躍遷的一維非厄米二聚化晶格示意圖.第sκ 個格點和第sκ+1 格點之間的躍遷振幅是不對稱的，為 t±(-1)jλFig.1.Schematic of the one-dimensional non-Hermitian mosaic dimerized lattice with asymmetric hopping.The backward and forwardward hopping amplitudes between the sκ-th and sκ+1-th sites are t ±(-1)jλ，which are asymmetric.

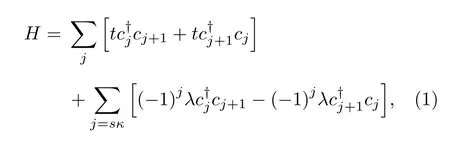
其中，(cj) 為格點j處的粒子產生(湮滅)算符.t為相鄰格點間的躍遷振幅，λ為格點間的非對稱躍遷強度.本文取t=1 作為能量單位且所有參數均為實數.κ為正整數，代表了鑲嵌型調制的周期;s的取值也為正整數，表明非對稱躍遷每隔κ個格點施加在躍遷振幅中.由于非對稱躍遷是正負交替變化的，這一模型具有二聚化晶格的特征.

2.2 有向性IPR(directional，IPR)

由于模型中存在非對稱躍遷，可以預期系統中將存在非厄米趨膚效應.在這一效應的影響下，系統在開邊界條件下的體態都會被局域在一維格點系統的兩端.系統本征態的局域性質可以通過計算其IPR(inversion participation ratio)來進行判斷.IPR 的定義為

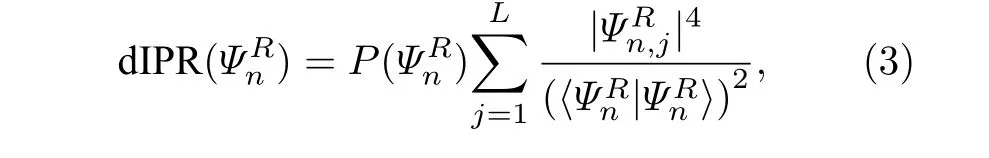
式中的P() 的定義為

sgn(x) 給出了變量x的符號:當x＞0 時為正，當x ＜0 則為負.δ為正數且取值為 0＜δ ＜0.5 .P()給出了本征態分布在系統的左半部分還是右半部分的信息，因而可以反映在非厄米趨膚效應下，本征態是被局域在一維格點系統的左端還是右端.當dIPR ＞0 時，說明該本征態局域在系統的右端;而如果dIPR＜0，則意味著該本征態局域在系統的左端.由此可見，可以用dIPR 來有效地對一維格點系統中的非厄米趨膚效應進行區分.

3 本征能譜、非厄米趨膚效應和拓撲零能態

3.1 本征能譜

首先考察一維非厄米鑲嵌型二聚化晶格在不同邊界條件下的本征能譜.圖2 給出了在開邊界條件下，具有不同周期(即κ)的鑲嵌型非對稱躍遷的二聚化晶格的本征能譜作為非對稱躍遷強度λ的函數圖像.從能譜的虛部(圖2 下半部分)可以看出，當非對稱躍遷強度|λ|＜t時，系統的本征能量為實數，因而系統在這一參數區域內具有純實數能譜.隨著|λ|的增大，系統的能譜不再保持為實數.當κ=1 時，非對稱躍遷被施加在所有的躍遷項上，可以發現系統的能量在|λ|＞t變為純虛數，因此系統的能譜在|λ|=t處經歷了實數能譜到虛數能譜的變化.而對于鑲嵌型調制的情況而言(κ＞1)，系統的能譜在|λ|＞t時變為復數.因此，在開邊界條件下，隨著非對稱躍遷的增強，系統的能譜會從實數變為虛數或復數，且發生這一變化的臨界點為|λ|=t.

接下來討論系統在周期邊界條件下的能譜性質，數值計算結果如圖3 所示.通過與圖2 中開邊界條件下的能譜進行比較可知，當κ=1 和 3 時，系統的能譜在不同邊界條件下具有相同的結構(邊界態除外)，且能譜在|λ|＜t的參數范圍內均為實數.而當κ=2 和4 時，系統在周期邊界條件和開邊界條件下的能譜結構則完全不同，且在周期邊界條件下，系統能譜在λ/=0 時即變成復數.通過進一步計算其他鑲嵌調制周期κ下的能譜，發現當κ為奇數時，系統在開邊界和周期邊界條件下的能譜是相同的(除邊界態外，見后文討論);而如果κ是偶數，則系統在不同邊界條件下的能譜具有十分不同的結構，與常規的具有非對稱躍遷的晶格模型的能譜特征類似.

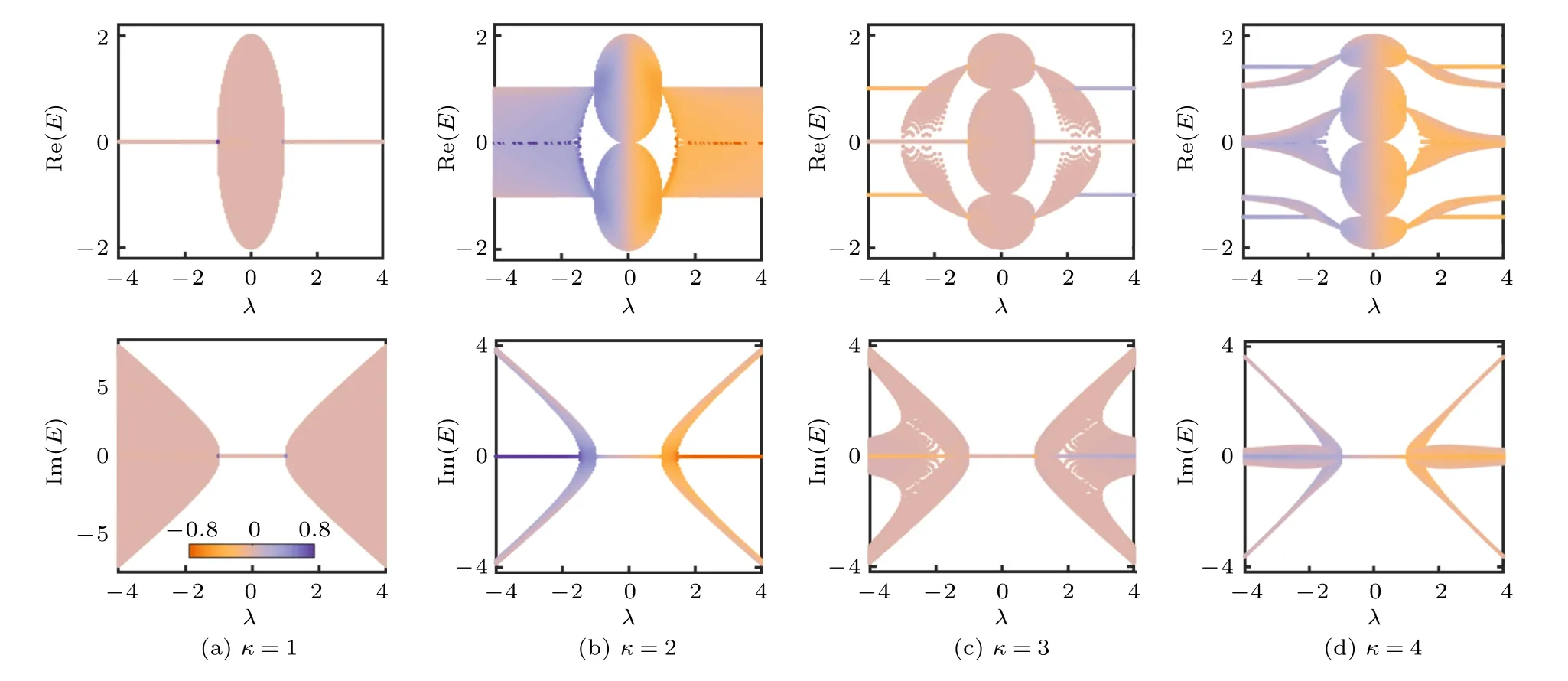
圖2 具有不同鑲嵌型調制的一維非厄米二聚化晶格模型在開邊界條件下的本征能譜.上半部分為能譜實部，下半部分為能譜虛部;圖中的顏色代表該能量對應的本征態的dIPR 值;系統大小為 L=120Fig.2.The eigenenergy spectra of the 1D non-Hermitian dimerized lattices with different mosaic modulations.The upper panel shows the real parts of the spectra while the lower panel shows the imaginary parts，the colorbar indicates the dIPR value of the eigenstate，the lattice size is L=120 .

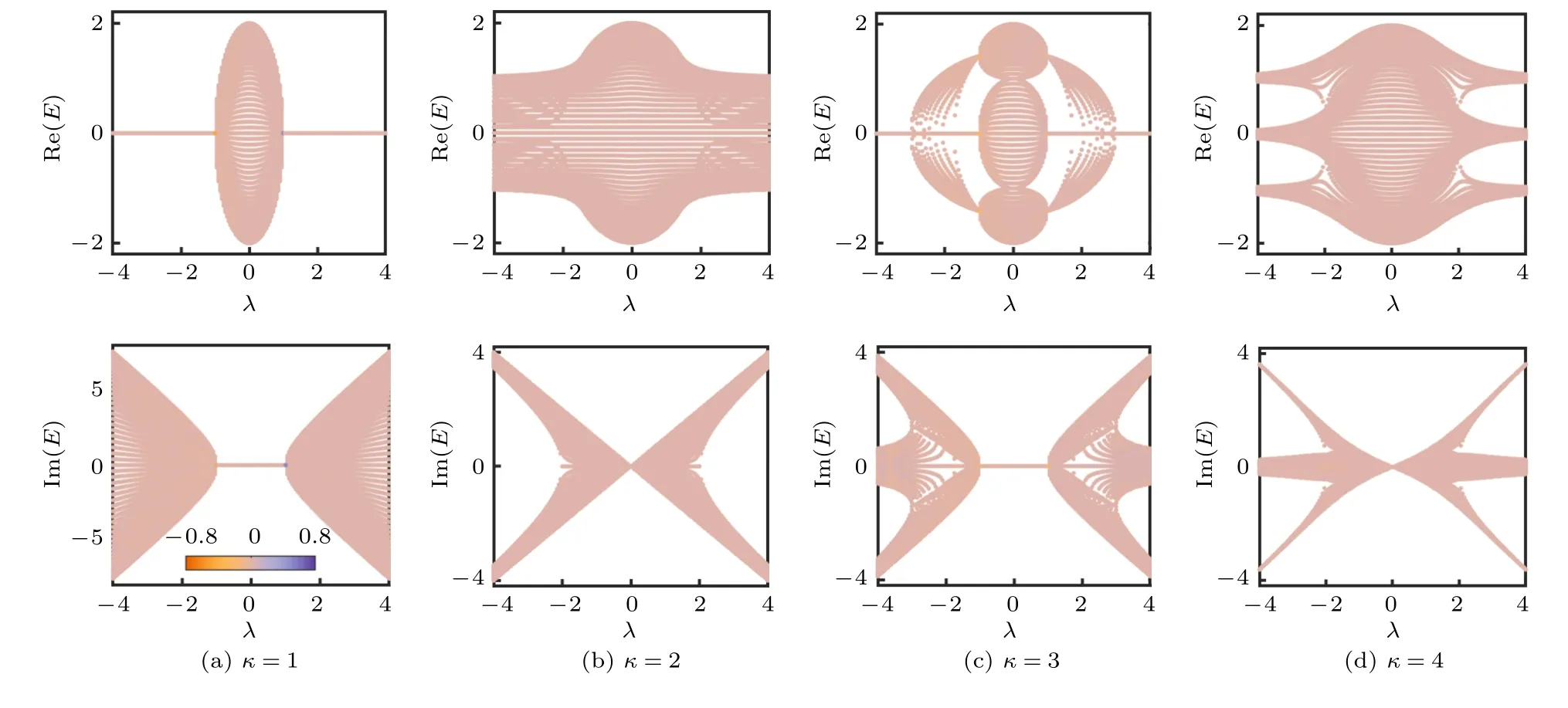
圖3 一維非厄米鑲嵌型二聚化晶格在周期性邊界條件下的本征能譜Fig.3.The eigenenergy spectra of the 1D non-Hermitian mosaic dimerized lattices under periodic boundary conditions.

3.2 非厄米趨膚效應

下面研究一維非厄米鑲嵌型二聚化晶格系統中的非厄米趨膚效應.圖2 中，數據點的顏色代表各個能量本征值所對應本征態的dIPR 值.由dIPR 的定義((2)式)可知，當dIPR＜0 時，對應的本征態被局域在晶格的左端;而如果dIPR ＞0，則該本征態局域在晶格的右端.從圖4 中可以發現，在κ為奇數時，所有體態的dIPR 值都趨于0，意味著這些體態均為擴展態，系統中沒有趨膚效應.當κ為偶數時，體態的dIPR 在λ＜0 的區域為正，而在λ＞0 的區域為負.此時，對應的本征態分別局域在一維晶格的右端和左端，如圖4(a)所示.λ=0 時，系統中不存在非對稱躍遷，因而沒有趨膚效應.為了更直觀表征趨膚效應在不同鑲嵌型調制周期下的表現，可以計算dIPR的平均值，即dMIPR，其定義為

圖4 具有非對稱躍遷的一維鑲嵌型二聚化晶格中的非厄米趨膚效應 (a) 在開邊界條件下，當本征態的 dIPR ＞0(dIPR ＜0)時，體態將局域在一維系統的右端(左端);(b) 系統的dMIPR 值在不同的鑲嵌型調制周期下的變化Fig.4.The non-Hermitian skin effect in the 1D mosaic dimerized lattices with asymmetric hopping:(a) Under open boundary conditions，the bulk eigenstates with d IPR ＞0(dIPR ＜0) will be localized at the right (left) end of the lattice;(b) the variations of dMIPR for the systems with different mosaic modulation.

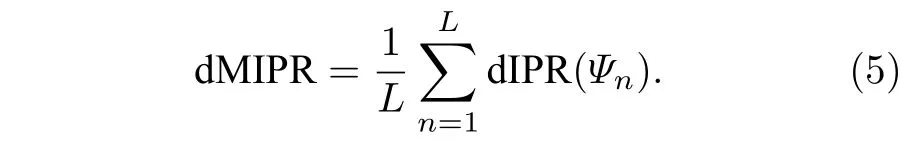
圖4(b)給出了dMIPR 作為λ的函數圖像.從圖中可以看到，在κ為奇數時，dMIPR 始終在0 附近，表明系統中不存在趨膚效應;而當κ是偶數時，dMIPR 則為有限值，且在λ=0 處由正值變為負值，對應于非厄米趨膚效應發生方向的改變.

非厄米趨膚效應在不同鑲嵌型調制周期下的不同表現也可以在能譜中反映出來(見圖2 和3).之前的研究已表明，非厄米趨膚效應與系統在周期邊界條件下能譜中的點能隙有關[53，54].圖5 也給出了系統在λ=1.5 時的能譜.可以看到，在沒有趨膚效應的系統中(即κ=1，3)，不同邊界條件下本征能量在復平面的分布是基本重合的，且周期邊界條件下的能譜沒有環狀結構，即不存在點能隙.但在κ=2，4 的系統中，其周期邊界下的能譜形成環狀結構，存在點能隙，對應開邊界下具有趨膚效應這一特征.

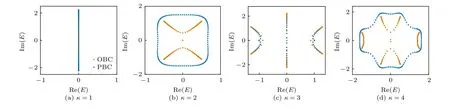
圖5 在 λ=1.5 時，系統在不同邊界條件下的能譜.棕色代表開邊界條件(OBC)下的能譜，藍色代表周期邊界條件(PBC)下的能譜Fig.5.The energy spectra under different boundary conditions of the system with λ=1.5 .The brown dots represent the spectra under OBC and the blue dots represent the spectra under PBC.

3.3 拓撲零能態

從圖2 的開邊界能譜圖可以發現，在某些情況下，系統中是存在拓撲邊界態的.為了更好判斷系統中是否存在拓撲零能邊界態，可以計算開邊界下系統能譜的絕對值，如圖6 所示.當κ=2 和 4 時，系統存在拓撲零能邊界態，且拓撲非平庸區域與平庸區域的臨界值為|λc|≈1.42 .

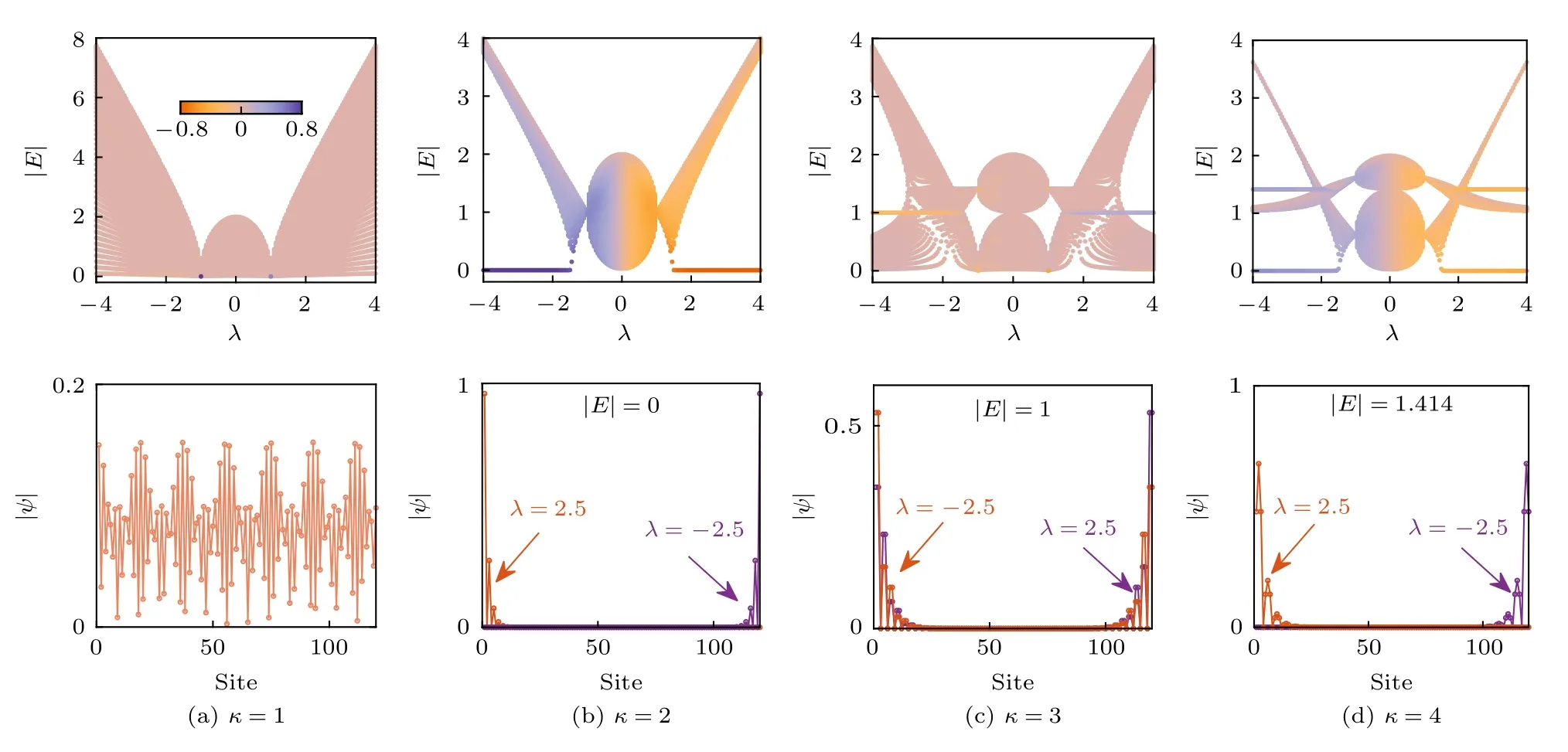
圖6 一維非厄米鑲嵌型二聚化晶格在開邊界條件下能譜的絕對值(上圖)，圖中的顏色代表該能量對應的本征態的dIPR 值，系統的大小為 L=120 ;不同 κ 值下，系統的本征態的空間分布(下圖)，κ=1 時，系統的本征態都為擴展態;κ=2 和4 時，系統中存在局域在邊界上的 零能拓撲態.此外，在 κ=3 和4 時，系統中分別存在能量為|E|=1 和|E|=1.414 的邊界態Fig.6.The absolute values of the eigenenergies of the non-Hermitian mosaic dimerized lattices (upper)，the colorbar indicates the dIPR value of the eigenstates，the lattice size is L=120 ;the distribution of eigenstates for systems with different κ values(lower)，when κ=1，the eigenstates are extended.When κ=2 and 4，there are topological zero-energy edge modes in the system.In addition，in the systems with κ=3 and 4，there are also edge states with energies|E|=1 and|E|=1.414，respectively.

為表征系統中拓撲零能邊界態，可以計算系統的貝里相位.由于存在非厄米趨膚效應，需要使用非布洛赫能帶理論(non-Bloch band theory)[41，42].對于鑲嵌調制周期為κ的格點系統，其原胞中的格點數q為2 和κ的最小公倍數，即q=lcm(2，κ) .系統在動量空間中的布洛赫哈密頓量可以表示成一個q×q維的矩陣，且其矩陣元為

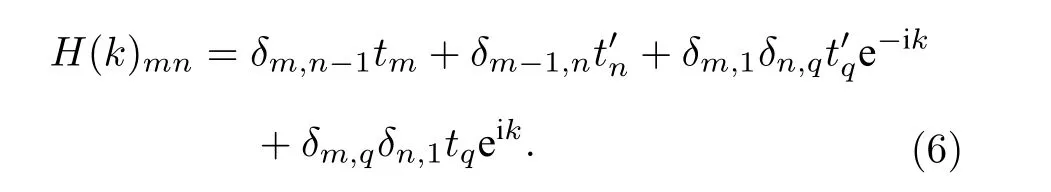
在此基礎上，根據非布洛赫能帶理論，做如下替代:eik →β=reik.例如，對于κ=4 的系統，其哈密頓量可改寫為

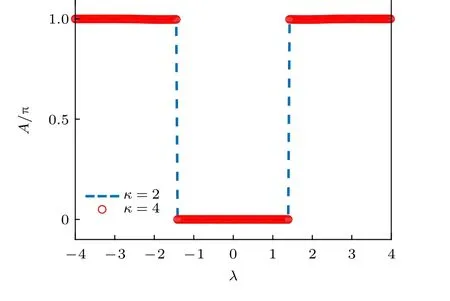
圖7 一維非厄米鑲嵌型二聚化晶格在 κ=2 (藍色虛線)和 κ=4 (紅色空心圓點)時的貝里相位.數值結果分別是將本征能量的實部小于零的能帶的貝里相位相加得到，從而表征系統中出現的拓撲零能邊界態Fig.7.The Berry phase for the 1 D non-Hermitian mosaic dimerized lattices with κ=2 (blue dashed line) and κ=4(red empty circles).The numerical results are obtained by summing up the Berrry phases of the bands with the real part of the eigenenergies smaller than 0 and thus characterize the existence of topological zero modes.

除了拓撲零能邊界態外，在κ=3 和 4 的開邊界能譜中還可以看到非零能量的拓撲邊界態，且這些邊界態對應的能量為常數，不會隨著λ的變化而發生改變，如圖6(c)和(d)所示.

4 討論部分

從以上的討論中可以發現，一維非厄米鑲嵌型二聚化晶格的能譜和非厄米趨膚效應與鑲嵌型的非對稱躍遷的周期有緊密聯系.當κ為奇數時，系統中的非對稱躍遷在不同格點處會發生正負交替變化，使得整個系統中的非對稱躍遷被抵消，因而系統中不會出現非厄米趨膚效應.但如果κ是偶數，那么系統中的非對稱躍遷的符號不會隨格點位置發生變化，因此系統中會出現趨膚效應，且其能譜結構也會在不同邊界條件下表現出不同的特征.圖2 和3 中給出了κ=1，2，3，4 時的系統能譜.為表明這一特性的普遍性，本文進一步計算了該系統在κ=5，6，7，8 時在開邊界條件下的能譜，如圖8所示.從本征態的dIPR 可以看出，非厄米趨膚效應存在與否和κ是偶數還是奇數有關.此外，本文還計算了非厄米鑲嵌型二聚化晶格在不同尺度下的能譜，如圖9 所示.可以發現，前述的研究結論不隨系統尺度的變化而發生改變.

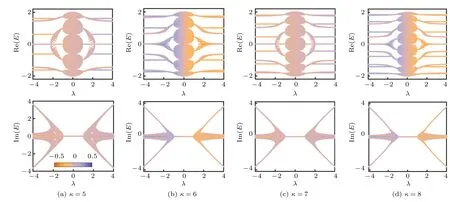
圖8 具有不同 κ 值的一維非厄米鑲嵌型二聚化晶格在開邊界條件下的能譜，圖中的顏色代表本征態的dIPR 值Fig.8.The eigenenergy spectra of the one-dimensional non-Hermitian mosaic dimerized lattices with different κ values under open boundary conditions.The color bar indicates the of the dIPR values eigenstates.

圖9 具有不同尺度的一維非厄米鑲嵌型二聚化晶格在開邊界條件下的能譜 (a1)—(a4)和(b1)—(b4)分別對應 κ=2 和3 的系統Fig.9.The energy spectra of the one-dimensional non-Hermitian mosaic dimerized lattices with different sizes under open boundary conditions，(a1)—(a4) and (b1)—(b4) correspond to the systems with κ=2 and 3，respectively.

此外，由于系統在動量空間的布洛赫哈密頓量H(k) 是一個q×q維矩陣，而q=lcm(2，κ)，所以q始終為偶數.可以證明:

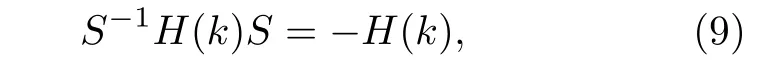
其中，S=diag(1，-1，1，-1，···，1，-1) 是一個q×q維的對角矩陣.因此，系統中存在子晶格對稱性(sublattice symmetry).盡管如此，由前述的數值結果可以發現，只有在κ為偶數的系統中存在拓撲零能邊界態，而當κ為奇數時，系統中不存在拓撲零能邊界態.綜上，將一維非厄米鑲嵌型二聚化晶格的性質總結見表1.

表1 具有不同 κ 值的一維非厄米鑲嵌型二聚化晶格的性質Table 1.The eigenenergy spectra of the one-dimensional non-Hermitian mosaic dimerized lattices with different κ values.

5 結論

本文引入了一類具有鑲嵌型非對稱躍遷的一維晶格模型.通過分析系統的本征能譜和本征態性質，發現鑲嵌型非對稱躍遷的周期對系統的性質具有顯著的影響.當鑲嵌型調制周期為奇數時，系統中沒有非厄米趨膚效應，其本征能譜在開邊界和周期邊界條件下是相同的(除拓撲邊界態外).如果鑲嵌型調制周期為偶數，那么系統中存在非厄米趨膚效應，且本征能譜在不同的邊界條件下具有完全不同的結構.本文還分析了這類系統中的拓撲態，討論了系統中的拓撲零能邊界態及其表征.本研究的結果表明，通過改變一維格點系統中的非對稱躍遷的施加方式和周期，可以改變系統中的非厄米趨膚效應以及系統中的拓撲邊界態，從而進一步揭示了非厄米系統特別是具有非對稱躍遷的非厄米系統的新奇特性.