翼型繞流的多級分辨率光滑粒子流體動力學數值模擬研究

黃曉婷, 孫鵬楠, 呂鴻冠, 殷曉瑞, 董嘉徐

(1.中山大學 海洋工程與技術學院, 廣東 珠海 519082;2.南方海洋科學與工程廣東省實驗室(珠海), 廣東 珠海 519082)

近年來,微型飛行器或潛水器的發展受到廣泛關注,飛行器或潛水器性能的改進離不開對翼型繞流問題的精確模擬。翼型表面流動如分離、附著等現象對翼型的動力性能具有重要影響。為保證在不同工況下飛行器或潛水器運行的可靠性,需要了解翼型繞流的流動特性和機理。這就要求對翼型繞流現象進行深入研究和分析。

翼型的幾何形狀對改善力學性能具有重要影響[1]。可以發現,目前對于非對稱翼型的繞流現象的研究較少。其中,Anyoji等[2]經過研究發現,非對稱Ishii弧形翼型由于后緣附近的弧度,其壓力阻力要遠遠小于其他對稱翼型,在同等工況下,可獲得比對稱翼型更高的升力。因此,展開對Ishii非對稱翼型更深入研究,準確獲取流場信息及其運動特性,可為未來設計出良好動力性能的新型翼型提供新思路。

現有翼型繞流研究中,主流研究方法中主要有試驗法及數值模擬法。針對水翼繞流,季斌等[3]從試驗和數值模擬角度綜述水翼水動力特性。在飛行氣翼繞流探究中,Anyoji等[2]采用風洞試驗探究及驗證Ishii翼型氣動性能。然而在試驗法中,試驗條件復現存在一定挑戰,且邊界層湍流細節捕捉對儀器的精密性要求苛刻。此外,試驗法的成本高昂,且對多工況無法同時進行研究。因此現有研究大多采取數值模擬法展開研究。數值模擬法中，發展較為成熟的歐拉網格法較為常見。但對于網格法而言,翼型后緣狹窄尖角邊界層較薄,網格劃分邊界層存在一定難度[4],在網格離散中需要較高的網格構建技術來滿足復雜的邊界條件。值得注意的是,近年來發展的無網格法對邊界條件、自由液面及大變形等問題[5]處理具有固有優勢。

SPH方法作為無網格法中應用廣泛的方法,在流體或固體力學問題處理中逐漸發揮重要作用[6]且對于自由液面變形動邊界問題的處理上SPH方法具有顯著優勢[7]。目前,在水動力學領域上得到較多應用[8-9]。Sun等[10]采用δ+-SPH模型對NACA0012翼型固定及自由運動狀態進行模擬,分析其水動力特性。Huang等[11]采用SPH方法對翼型繞流的運動性能進行探究;在空氣動力學領域,Shadloo等[12]驗證了WCSPH可以實現低雷諾數下不同攻角翼型繞流計算;Huang等[13]采用KGF-SPH模型,在低雷諾數下對氣翼的升阻力系數進行監測,驗證該模型的準確性。可得出,SPH方法在翼型繞流問題研究上具有一定的優勢及特色。但由于其本身的精度及穩定性問題,SPH方法在翼型氣動性上的研究受到一定限制,翼型繞流中邊界層內部流場特征獲取仍需進一步的方法改進和技術討論。

因此,本文克服以往SPH方法難以模擬黏性邊界層流動的不足,采用δ+-SPH模型,實現黏性流動下翼型繞流的模擬,展開翼型特性分析。在SPH計算中,高雷諾數下翼型繞流模擬存在三大難點,主要應用以下方法進行解決:①針對流體繞過翼型時,由于負壓產生的張力不穩定現象,采用張力不穩定性控制(tensile instability control,TIC)技術,實現Ishii翼型黏性繞流的壓力場和速度場等穩定數值模擬。②為了避免粒子的拉格朗日結構引起的計算精度下降現象,在每個時間步初始時刻,施加粒子修正技術(particle shifting technique,PST),確保粒子的均勻分布。③為實現邊界層黏性力的精確計算,采用自適應粒子細化(adaptive particle refinement,APR)技術,減少粒子數量,提高計算效率,實現粒子高分辨率同時確保計算精度。

1 δ+-SPH模型

在δ+-SPH模型中,考慮流體的真實物理黏性,在動量方程中施加黏性項,以精確模擬邊界層的流動。再有,在連續方程中添加密度耗散項[14],以避免高頻的壓力振蕩。此外,為了避免傳統SPH模型中由于粒子的拉格朗日結構引起的計算精度降低現象,δ+-SPH模型針對粒子進行位移修正,引入粒子位移修正技術(particle shifting technique,PST),確保在計算過程粒子分布的均勻性。因此,基于流體弱可壓假設下,δ+-SPH模型[15]最終寫為

(1)

式中：i和j表示支持域內目標粒子及其對應的鄰近粒子；fi是質量力,本文計算均取fi=0；ρi,mi,Vi,ui,ri分別代表粒子i的密度、質量、體積、速度和位移；光滑核函數Wij采用Wendland的C2核函數[16],光滑長度h=2Δx,其中Δx是初始粒子間距；耗散項Di和πi的具體參數可參考文獻[15]。Fij為壓力項,在本文中采用張力不穩定控制技術進行處理。

為確保粒子的均勻分布,在δ+-SPH模型中,動量方程計算得出的粒子位移ri需要施加人工位移修正量δri,δri具體定義為

(2)

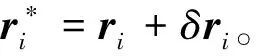
2 張力不穩定性控制技術

在傳統SPH模型中,由于負壓會導致張力不穩定現象[18],流場信息將無法很好呈現。基于Sun等[15]的研究結果,為更好實現漩渦附著、分離、脫落細節的捕捉,展開對Ishii翼型流場規律分析,本文采用TIC技術改進壓力梯度項。對壓力項Fij進行改進[15]，如(3)式所示

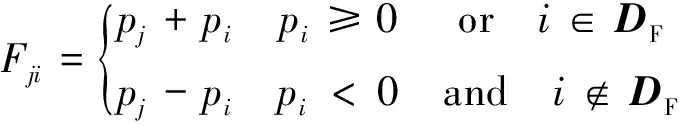
(3)

DF表示液面區域自由液面粒子及相鄰粒子的集合。

3 拉格朗日擬序結構可視化

在歐拉算法的模擬結果中,流場特征量(如渦量)通常基于歐拉框架下的瞬態速度場計算得出,難以給出流體介質在某個時間段內的輸運特征,而本文采用拉格朗日擬序結構對流場中漩渦結構進行可視化,可更加清晰地獲取流場細節。拉格朗日擬序結構通過計算有限時間李亞普諾夫指數(finite-time Lyapunov exponent,FTLE)實現。在FTLE云圖中呈現的脊線為拉格朗日擬序結構[19]。

在SPH計算程序中采用逆向FTLE展開對FTLE計算,以便能清晰反映漩渦結構邊界特征[20]。逆向FTLE計算方程為

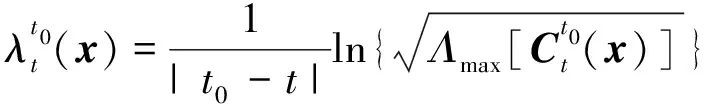
(4)

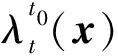
4 多級粒子分辨率技術

翼型的首尾部往往較為狹窄,翼型繞流中表面邊界層內湍流流動的捕捉對于網格法和無網格法均具有一定挑戰性。因此,本文將利用多級粒子分辨率技術[21],將翼型表面離散成分辨率高的固定虛粒子,實現精確捕捉湍流流動細節,提高邊界黏性力的計算精度。多級粒子分辨率技術原理如圖1所示。

圖1 多級粒子分辨率技術原理示意圖[21]

主要原理闡述如下:不同分辨率的粒子定義為不同的粒子集合。首先定義翼型附近區域為細化區,在細化區邊緣定義過渡區,如圖1b)所示,充當其邊界條件,獲取進入細化區域母粒子的信息。過渡區域的寬度設置要大于核函數的半徑,防止其邊緣處核函數截斷而造成計算誤差。在計算中,參與流場SPH計算的粒子稱為SPH粒子;活性關閉,不參與SPH計算的粒子為非活性粒子。在細化區,母粒子分裂,如圖1a)所示,在正方形4個頂點處形成更小粒子即子粒子,子粒子活性激活,參與流場的SPH計算,即為SPH粒子。而母粒子在撕裂之后,作為非活性粒子不再參與SPH計算,但仍然隨著流場運動,通過從周圍細化的子粒子插值獲得流場信息如速度、壓力等。相反的,在過渡區域,母粒子為SPH粒子,子粒子屬性從周圍SPH粒子即母粒子插值得出。采用Shepard插值方法,非活性粒子的物理量φ從周圍SPH粒子完成插值,插值公式為

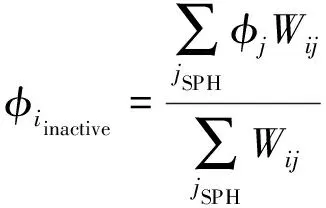
(5)

經過此過程,2層分辨率粒子完成了相互之間的信息交換。多級粒子分辨率技術對局部流場粒子加密,在不同的分辨率區域之間,過渡區域及細化區域并不隨著粒子的移動而移動。在計算中,當母粒子撕裂而來的子粒子流出細化區及過渡區域時,不發生粒子合并而將直接被刪除,而母粒子流出細化區域時,將正常參與SPH流場計算。基于以上粒子細化思想,在多層分辨率粒子間,保持粒子尺度一樣,每層粒子的過渡區域流場信息從下一層插值取得,從而實現不同層次間粒子信息交換,實現多級分辨率的SPH數值計算,提高流場計算精度。在下文將首先通過圓柱繞流基準算例驗證在δ+-SPH中添加多級粒子分辨率技術的有效性,從而應用于翼型繞流問題的研究中。

5 基準算例驗證

圓柱繞流問題是流體力學中的經典問題,是檢驗數值算法的經典算例。選取雷諾數Re=3 000,人工聲速c0=15 m/s時的圓柱繞流模擬算例,與試驗結果對比以檢驗δ+-SPH模型的數值精度。

在該算例中,施加多級粒子分辨率技術,采用5層分辨率不同的粒子。圓柱表面的粒子間距為D/Δx=400,最遠處粒子間距為D/Δx=25。在計算中,粒子總數為1.45×106。假設在計算域中粒子分辨率均取為D/Δx=400,粒子總數將達到7.68×107。可見,多級粒子分辨率技術對重點區域流場進行加密,在保證計算精度條件下,有效減少了粒子總數,從而減少計算時間,提高計算效率,對實現SPH方法在工程上應用具有重要意義。

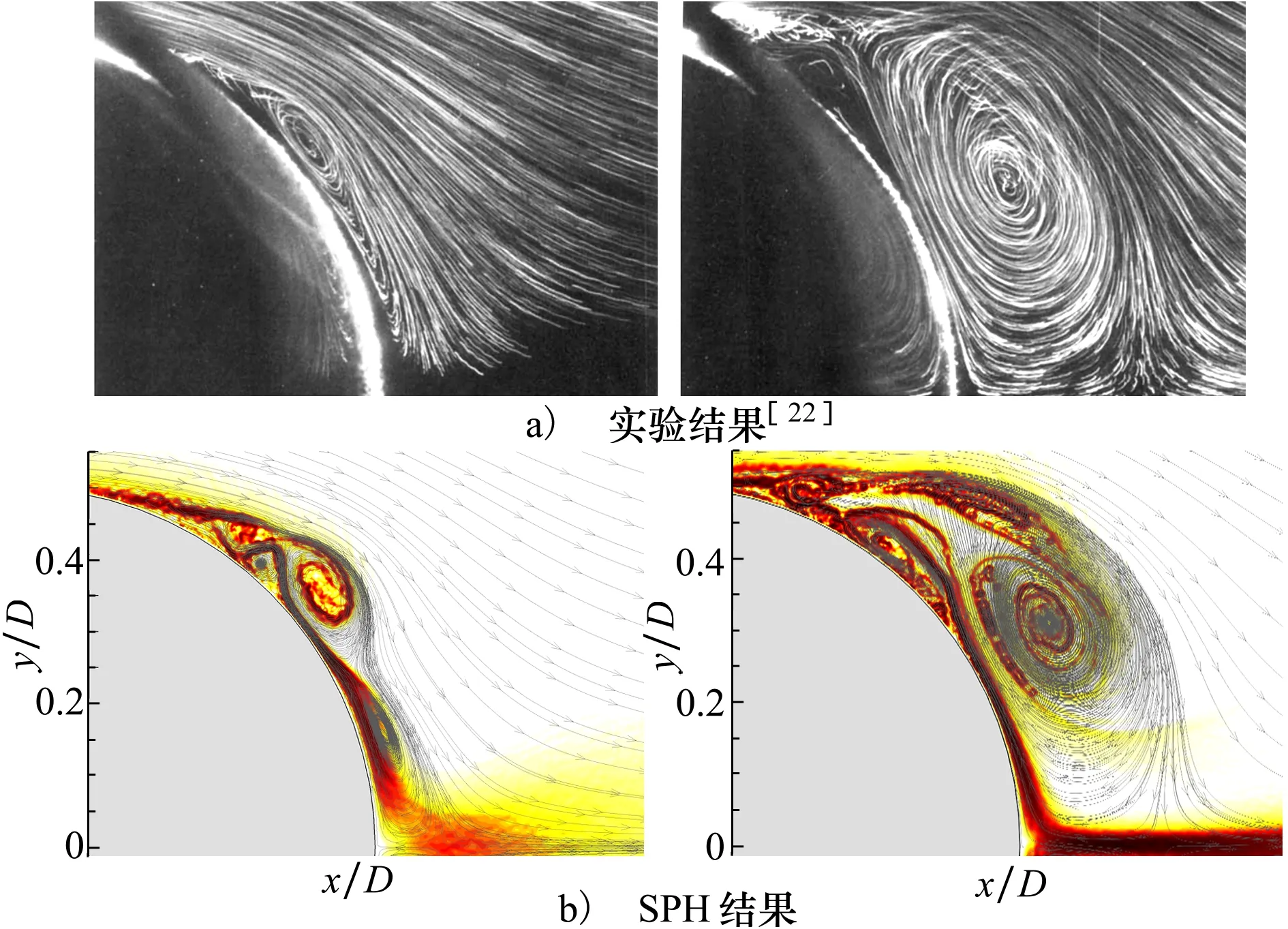
圖2 雷諾數Re=9 500圓柱繞流流場特征

圖2中選取圓柱上表面的δ+-SPH計算圖展示圓柱繞流的漩渦發展過程。通過漩渦流線圖與試驗結果[22]對比,可以發現試驗結果與δ+-SPH結果吻合良好。δ+-SPH模型與多級粒子分辨率技術相結合,漩渦發展細節能較好被模擬,δ+-SPH結合多級粒子分辨率技術可以較為準確模擬繞流現象中分離、附著現象。SPH中拉格朗日擬序結構能清晰展示漩渦演化過程,呈現清晰的內部細節,與試驗結果基本保持一致,說明拉格朗日擬序結構獲取流場特征的高精度。基于以上討論,可見SPH方法在漩渦結構捕捉等方面具有獨特優勢。在下節中,本文將采用多級粒子分辨率技術對計算域粒子進行處理,結合δ+-SPH計算結果中的拉格朗日擬序結構展開對翼型繞流現象研究。

6 Ishii翼型繞流

6.1 Ishii翼型繞流的初始工況和邊界條件設置

Ishii翼型具有翼厚比低、前緣半徑小等特征,翼型形狀[23]如圖3所示。本文模擬將Ishii翼型固定在矩形流場中,流場左側為流入邊界,來流速度設為U0=1 m/s,右側為流出邊界,上下邊界為自由滑移壁面邊界。翼型的上表面施加無滑移邊界條件。

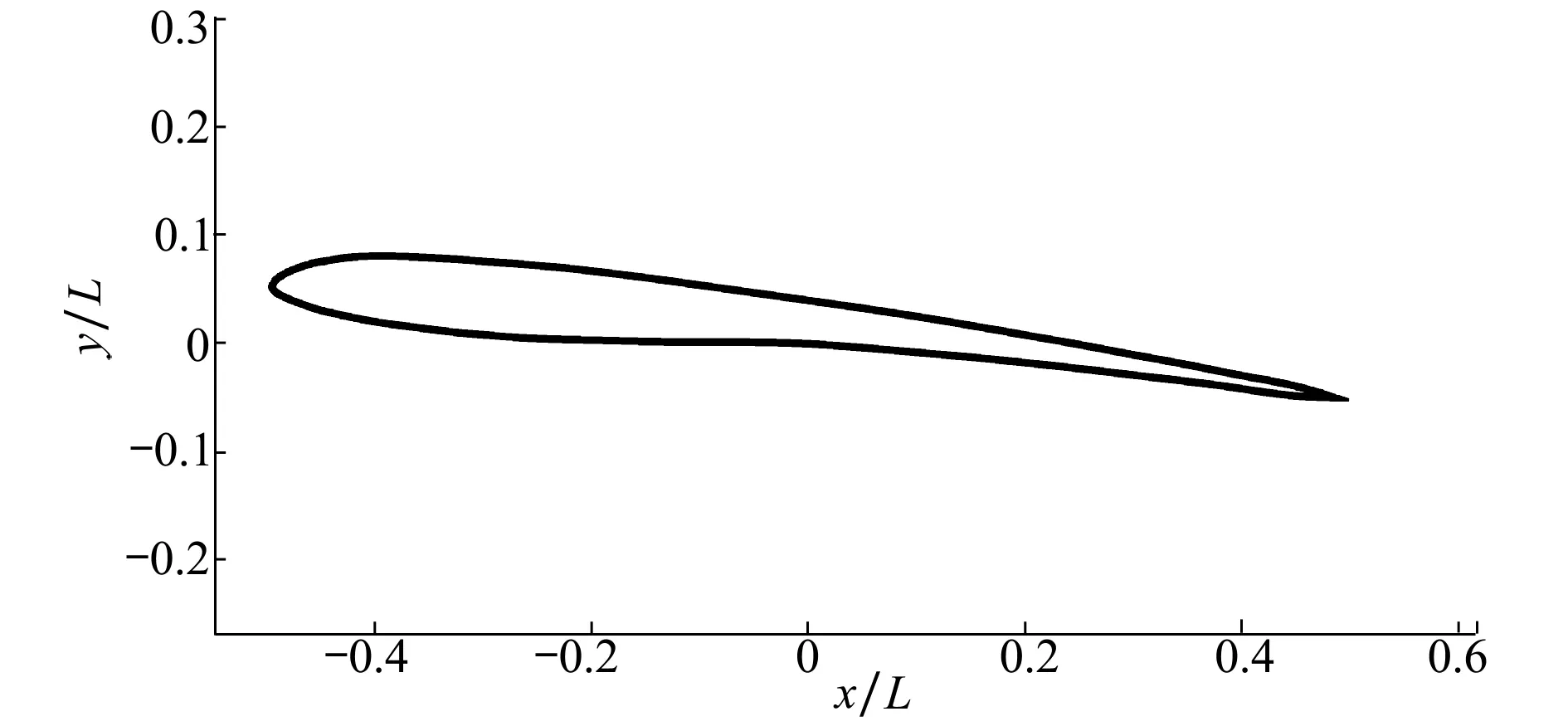
圖3 攻角α=6°時的Ishii翼型形狀

對Ishii翼型表面的無量綱量升阻力系數測量計算,獲取翼型的氣動力特性。對阻力系數CD,升力系數CL定義為：

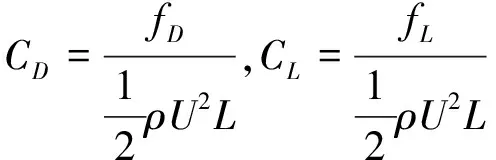
(6)

式中，fD和fL分別定義為繞流Ishii翼型的阻力和升力,在SPH程序計算中,這兩者的計算基于流體粒子與結構粒子之間相互作用力的平衡算得。在本文翼型模擬中,弦長L=1 m。

6.2 多級粒子分辨率技術對計算效率的提升

為提高計算效率,采用6層不同的粒子分辨率,在翼型表面的最高粒子分辨率為L/Δx=800,最低粒子分辨率即距翼型最遠處取L/Δx=25。在本計算中粒子總數為6.40×105,如果采用L/Δx=800對全流場進行計算,粒子總數將達到3.07×107,可見采用多級粒子分辨率技術,粒子總數減少將近43倍,除去不同尺度粒子之間的插值耗時,多級粒子分辨率技術可將計算效率提高約20倍。

6.3 雷諾數Re=3 000下繞流模擬結果和驗證

首先,在雷諾數Re=3 000、攻角α=0°條件下,模擬了Ishii翼型繞流特性。阻力系數的計算結果如圖4所示。FVM結果與SPH結果基本吻合,驗證了SPH方法的計算精度。

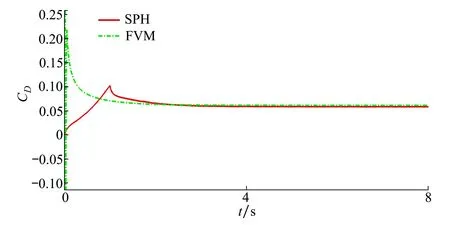
圖4 雷諾數Re=3 000, 攻角α=0°Ishii翼型阻力曲線

6.4 雷諾數Re=30 000下繞流模擬結果和分析

6.4.1 升阻力系數

隨后,在雷諾數Re=30 000、攻角α=0°,3°,6°條件下,模擬了Ishii翼型繞流的特性。α=6°時,翼型阻力及升力系數的SPH計算結果與FVM結果對比如圖5所示。在粒子初始階段到歷經劇烈抖動之后,最終CL在0.60～0.85之間動態波動。同樣地,曲線可發現阻力CD系數在0.044上下波動。

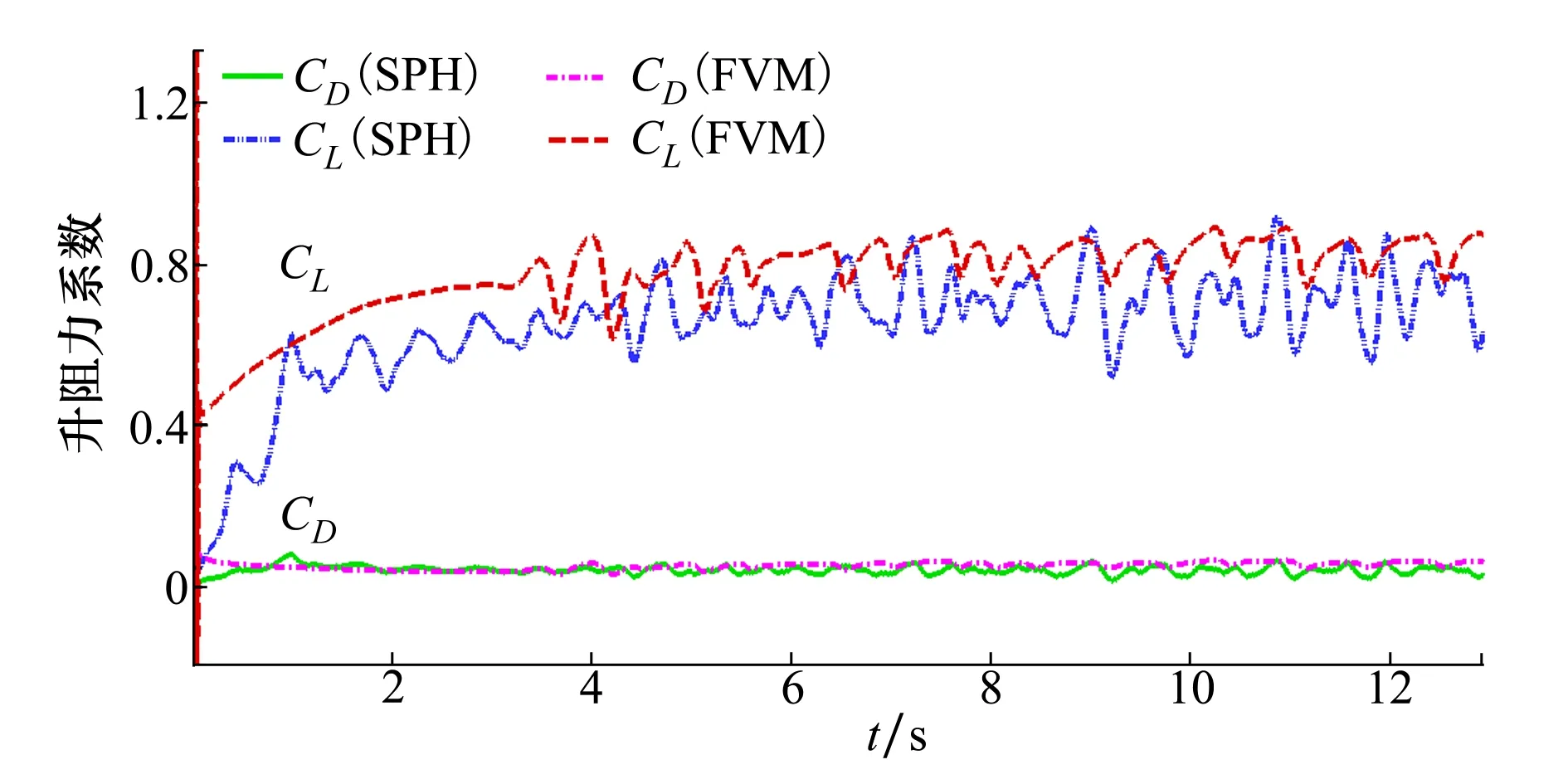
圖5 雷諾數Re=30 000下的升阻力系數時歷曲線

表1給出了本文計算結果及文獻中試驗結果[23]與其他數值結果[24](2-D Lam、2-D RANS)的對比。可以看出,多種算法的升阻力系數值基本吻合,SPH結果與2-D Lam計算結果吻合最佳。通過比較圖6中攻角α=0°,3°,6°的升力系數可以看出,攻角變大、升力系數增加。此外,攻角增大引起黏性漩渦的非周期性脫落,使得升力系數隨時間產生振蕩。

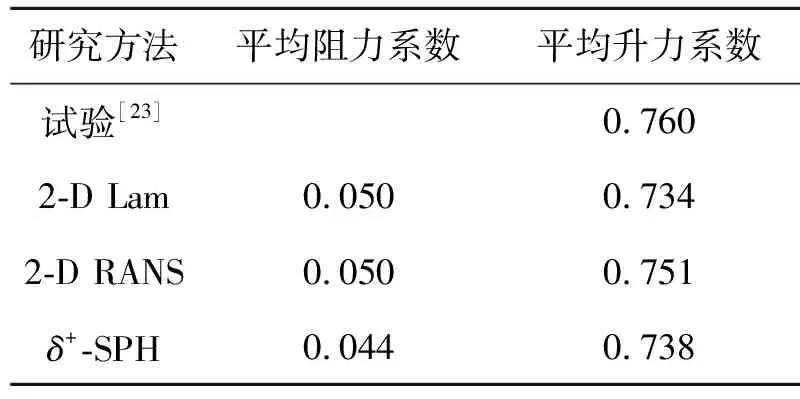
表1 升阻力結果驗證

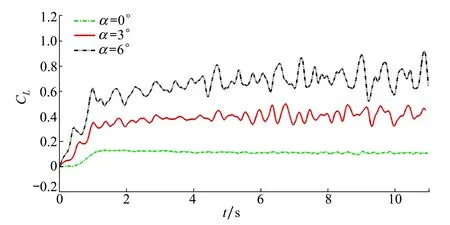
圖6 不同攻角α下升力系數時歷曲線

6.4.2 SPH計算黏性繞流問題的速度場與壓力場

圖7展示了雷諾數Re=30 000、攻角α=6°條件下,Ishii翼型繞流的速度場和粒子分布情況。

圖7 Ishii翼型繞流的速度場和粒子分布

對比t=0.7 s時刻,施加與不施加PST時的粒子分布,可見：不施加PST時,翼型周圍粒子分布十分不規則,且速度場呈現出不穩定;而施加PST,翼型表面邊界層內流體粒子分布十分均勻,保證了速度場計算的精度。

在SPH模擬中,實現穩定的壓力場計算至關重要。然而在傳統SPH算法中,常常存在壓力振蕩及張力不穩定性現象。在δ+-SPH模型中,通過在連續方程中添加密度耗散項[14],可得到光滑的壓力場。針對張力不穩定現象,本文采用張力不穩定性控制技術進行解決。為驗證其有效性,圖8中給出Ishii翼型繞流模擬中施加TIC與不施加TIC的壓力云圖。可見,不施加TIC時,翼型周圍流場中出現數值空洞,導致計算結果失真;施加TIC時,Ishii翼型周圍壓力分布均勻,且沒有數值噪聲。

圖8 壓力場云圖(t=4.076 s,Re=30 000)

以上對比說明,δ+-SPH模型結合TIC技術可以有效消除壓力噪聲,進而較好實現翼型的壓力數值變化預報。此外,觀察壓力云圖可以發現,翼型首部附近區域存在巨大負壓區,這是引起張力不穩定現象的主要原因。因此,采取張力不穩定性控制技術是準確獲取流場特征的重要前提。

6.4.3α=6°時Ishii翼型繞流中漩渦結構分析

圖9 翼型周圍流場中的漩渦結構(t=12.326 s,Re=30 000)

圖9給出了翼型周圍流場中的拉格朗日擬序結構和渦量場。可見,翼型表面附近高分辨率粒子的布置使得邊界層內湍流細節能能夠清晰地捕捉,反映出多級粒子分辨率技術在高雷諾數下黏性繞流問題中的重要作用。相比于渦量場(網格法較常使用該方法捕捉漩渦結構),在SPH框架中捕捉的拉格朗日擬序結構更能清晰重現渦結構的輪廓和內部細節。此外,相較于渦量場云圖,FTLE云圖受閾值的影響不敏感,更加便于進行流場細節分析。這也是SPH粒子法處理翼型繞流問題的優勢之一。

從圖9可見,在翼型形狀及壓力梯度影響下,Ishii翼型漩渦的生成、附著、分離等主要發生在翼型上緣。基于多級粒子分辨率技術,可以發現,尺度很小的漩渦也能清晰捕捉,再次說明了多級粒子分辨率技術的有效性。

7 拓展應用:拍動翼型繞流問題

為進一步展示SPH在處理運動翼型繞流問題中的優勢,本節采用δ+-SPH模型對拍動水翼問題進行模擬和驗證。在網格法中,對運動翼型繞流問題的模擬容易引起網格變形而降低計算精度。即使采用重疊網格法,也常常因涉及不同網格間的插值而使算法變得復雜。相比而言,得益于SPH的拉格朗日粒子特性,對于大幅運動邊界問題的模擬較為方便。

本節選擇頭部半圓尾部尖角的拍動翼型(具體細節參考文獻[25])進行SPH計算與驗證;采用無量綱參數包括雷諾數Re、斯特勞哈爾數Sr、幅值無量綱系數AD表征流體黏性、翼型拍動頻率、翼型拍動振幅對翼型繞流模擬的影響。拍動幅值無量綱系數AD=2A/D,其中,A為翼型拍動最大幅值,D取為翼型頭部半圓直徑。

圖10給出了雷諾數Re=440,斯特勞哈爾數Sr=0.035,無量綱幅值系數AD=1.47條件下,SPH模擬的漩渦結構與試驗結果[25]的對比。在t1時刻,SPH結果與試驗結果[25]吻合較好,體現了δ+-SPH模型在運動翼型繞流模擬上的精度和獨特優勢。觀察SPH不同時刻的結果,可見拉格朗日擬序結構能呈現拍動翼周期拍動時漩渦演化過程,這為未來翼型推進性能與漩渦關系的研究提供了新思路。

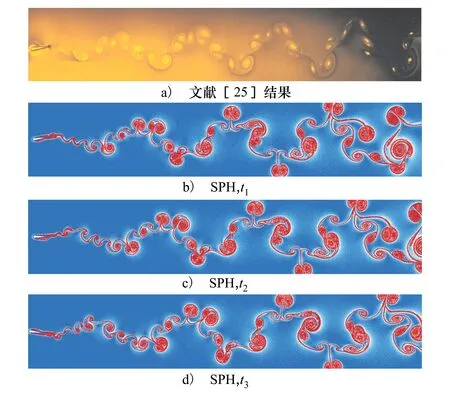
圖10 拍動水翼繞流尾跡的試驗結果[25]與SPH結果

8 結 論

本文采用δ+-SPH方法對不同雷諾數和攻角下的翼型繞流問題進行了數值模擬研究,分析了升阻力特性和流場漩渦特征,并將SPH方法從固定翼繞流拓展應用到了拍動翼繞流的模擬中。研究結果表明:

1) SPH方法在模擬真實黏性邊界層和漩渦運動的流體動力學問題中具有競爭力。不同于網格法,SPH方法易于實現拉格朗日擬序結構的捕捉,動態呈現漩渦結構演化過程,因此在未來探究漩渦與流體動力特性關系上具有重要優勢。

2) 采用TIC技術及PST技術能夠有效提高翼型繞流的速度場和壓力場計算精度,并實現對升阻力系數較高精度的預報;采用多級粒子分辨率技術能夠有效減少粒子總數,縮短計算時間,從而便于在工程中應用。

3) SPH方法不需要生成網格,能自動追蹤運動和變形的流固界面,而且該方法的拉格朗日和無網格粒子特性使其在模擬運動翼型繞流問題上具有先天優勢和巨大潛力。在未來研究中,利用該優勢,SPH方法在翼型繞流的渦振或顫振問題研究中有望發揮重要作用。