基于Franc3D的水陸兩棲飛機涉水結構損傷容限分析

賀爾銘, 李巍, 薛小鋒, 賈志艷, 馮蘊雯

(1.西北工業大學 航空學院, 陜西 西安 710072; 2.中航通飛華南飛機工業有限公司, 廣東 珠海 519090)

水陸兩棲飛機的涉水結構不僅長期處于高溫、高濕、高鹽等腐蝕環境，還經常在波浪水面滑行、起降時出現升沉、跳躍，導致較大的過載及復雜的水動力沖擊，因此其涉水結構大多采用損傷容限設計，并須對其進行損傷容限分析[1]。

羅琳胤等[2]基于LS-DYNA仿真平臺建立了飛機結構和水體耦合的數值模型，采用ALE耦合算法分析了飛機著水時重心過載、機身底部壓力的變化過程，并研究了著水攻角、下沉速度及升力對著水過載特性的影響。Sun等[3]采用數值造波方法實現了水陸兩棲飛機的波面著陸模擬，并通過水池模型試驗驗證了該方法的準確性。目前研究多集中于水陸兩棲飛機水動載荷特性，對用于涉水結構損傷容限分析的載荷譜研究較少。

裂紋擴展分析是損傷容限分析中最重要的部分。水陸兩棲飛機涉水結構主要使用鋁合金制造，目前已經有一定的工作對鋁合金在腐蝕環境下裂紋擴展特性進行了試驗研究[4-5]，測定了不同環境下鋁合金的裂紋擴展參數。Meng等[6]對7075鋁合金在海水腐蝕環境下，溶液濃度、溫度及載荷頻率對其裂紋擴展速率的影響進行了試驗研究，并提出了考慮腐蝕電流、載荷頻率的裂紋擴展模型。Chemin等[7]對7075-T351鋁合金在TWIST隨機載荷譜作用下、鹽霧環境中裂紋擴展速率進行了研究。相關研究為涉水結構在腐蝕環境下的裂紋擴展仿真提供了參考。應力強度因子計算是裂紋擴展分析的基礎。目前的方法主要有解析法、有限元法、邊界元法、權函數法等[8-9]。其中有限元法應用最為廣泛，精度較高，但其對裂紋擴展時裂紋尖端重構網格質量有較大的要求，操作較為復雜。Franc3D是美國FAC公司開發的新一代裂紋分析軟件，它結合有限元軟件進行斷裂力學計算，具有較高的精度[10]。但該軟件在進行擴展壽命計算時，內置的裂紋擴展模型未考慮載荷作用次序對壽命的影響。

本文考慮水載荷的影響，在TWIST標準運輸機載荷譜的基礎上，編制用于水陸兩棲飛機損傷容限分析的隨機載荷譜；利用Franc3D和ABAQUS聯合仿真，對某涉水框結構進行腐蝕環境下裂紋擴展分析；使用Willenborg/Chang模型計算裂紋擴展壽命，并確定了檢查門檻值和檢查間隔，建立了水陸兩棲飛機涉水結構損傷容限分析的流程。

1 損傷容限分析流程

飛機結構的損傷容限分析主要分為裂紋擴展分析、剩余強度分析及損傷檢查三部分內容。其中，兩棲飛機涉水結構損傷檢查方法與普通飛機沒有太大差異。研究表明，腐蝕環境下的裂紋失穩擴展仍受同一個Kc控制，即剩余強度不受腐蝕影響[5]，剩余強度分析方法與實驗室環境下相同。因此對水陸兩棲飛機損傷容限分析的重點為涉水結構的裂紋擴展分析。鋁合金表面在腐蝕環境下會形成腐蝕坑，裂紋往往萌發于這些腐蝕坑，相對于無腐蝕的情況，裂紋萌生壽命更短[11]。一般來說，腐蝕環境對金屬結構裂紋擴展有加速作用，所以對涉水結構進行腐蝕環境下的裂紋擴展分析是很有必要的。需要通過損傷容限分析來確定檢查門檻值和檢查間隔，以保證飛機的飛行安全。

1.1 涉水結構的腐蝕環境

腐蝕環境對鋁合金裂紋擴展有加速作用,本文采用波音方案,即Paris或Walker公式中除C以外其余常數不變,采用室溫時數據,只轉換公式中的常數C[12],公式為

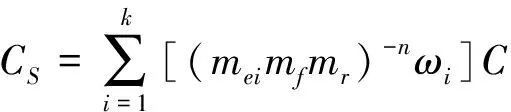
(1)

式中:C,n為實驗室空氣和溫度下Paris或Walker公式中的常數;mei為材料裂紋擴展環境系數。mf為頻率效應;mr為對合金鋼應力比下環境、頻率綜合效應;ωi為飛機環境加權百分數,即第i種標準實驗室環境在飛機飛行環境中占的比例。對本文鋁合金結構,mf,mr取1。

對參數C的修正體現了環境對裂紋擴展速率的影響。對于兩棲飛機來說,涉水結構面臨海水和淡水的腐蝕環境,腔體結構還會聚集水汽,相應地,要提高3.5%NaCl溶液、蒸餾水、潮濕空氣這幾種腐蝕環境的比例。2024-T3鋁合金環境參數見表1。

表1 2024-T3鋁合金環境參數

1.2 涉水結構的模擬載荷譜編制

通常水陸兩棲飛機水上起降次數是陸上起降的4～10倍[2]。飛機在水面滑跑、起降時會承受復雜的水動載荷,其中載荷水平較大的有中高速滑行時波浪對機身船體的沖擊力和水面降落時機身船體與水面的撞擊力。由于缺乏水陸兩棲飛機的載荷譜試驗數據,本文在TWIST運輸機標準載荷譜的基礎上,加入水載荷對應的載荷水平及頻次,作為編制水陸兩棲飛機損傷容限分析載荷譜的基礎。TWIST載荷譜規定了4 000次飛行循環(100周期/飛行循環),包含10類飛行類型及載荷等級[13],如表2所示。

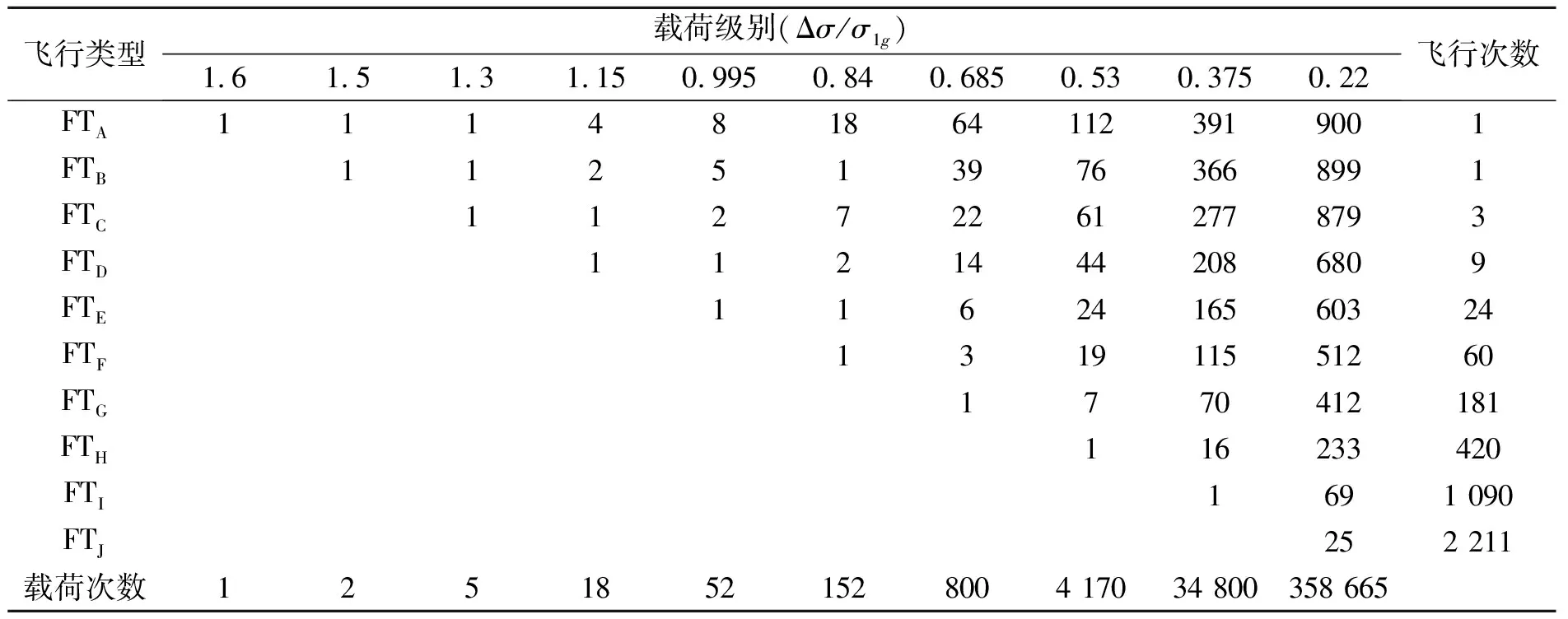
表2 TWIST標準譜中10種飛行類型對應各級陣風載荷及機動載荷出現次數

載荷級別由Δσ/σ1g的形式給出,以載荷級別為1.3為例,則該載荷級別對應的峰谷值為

將1 000次飛行中出現次數小于10的載荷進行高載截取,即將載荷級別為1.6,1.5的載荷處理為載荷級別為1.3的載荷。TWIST原譜對地面載荷的處理辦法為在每個飛行類型間增加載荷級別為-0.3的載荷循環。對于兩棲飛機,將載荷水平增大至載荷級別為-0.5。文獻[2]中對某型水陸兩棲飛機在2/3升力情況下水面著陸進行仿真,其重心過載在-0.3g～1.3g間變化。假設應力與重心過載成線性關系,且水上起降次數為陸上起降的7倍,給每個飛行類型隨機插入7組谷值為-0.3σ1g,峰值為1.3σ1g的載荷。

在Matlab中首先使用隨機排序函數,模擬出不同飛行類型出現的順序。相同幅值的峰、谷值不一定是一一對應的,對每一個飛行類型,首先分別羅列出包含的所有峰值和谷值,對峰值和谷值序列分別進行隨機排序,將排序后的峰谷值一一對應,即可生成載荷序列。載荷譜中一共包含4 000次飛行、426 665個循環,如圖1所示,并給出了第四個飛行循環,飛行類型為FTi的載荷譜示意圖。

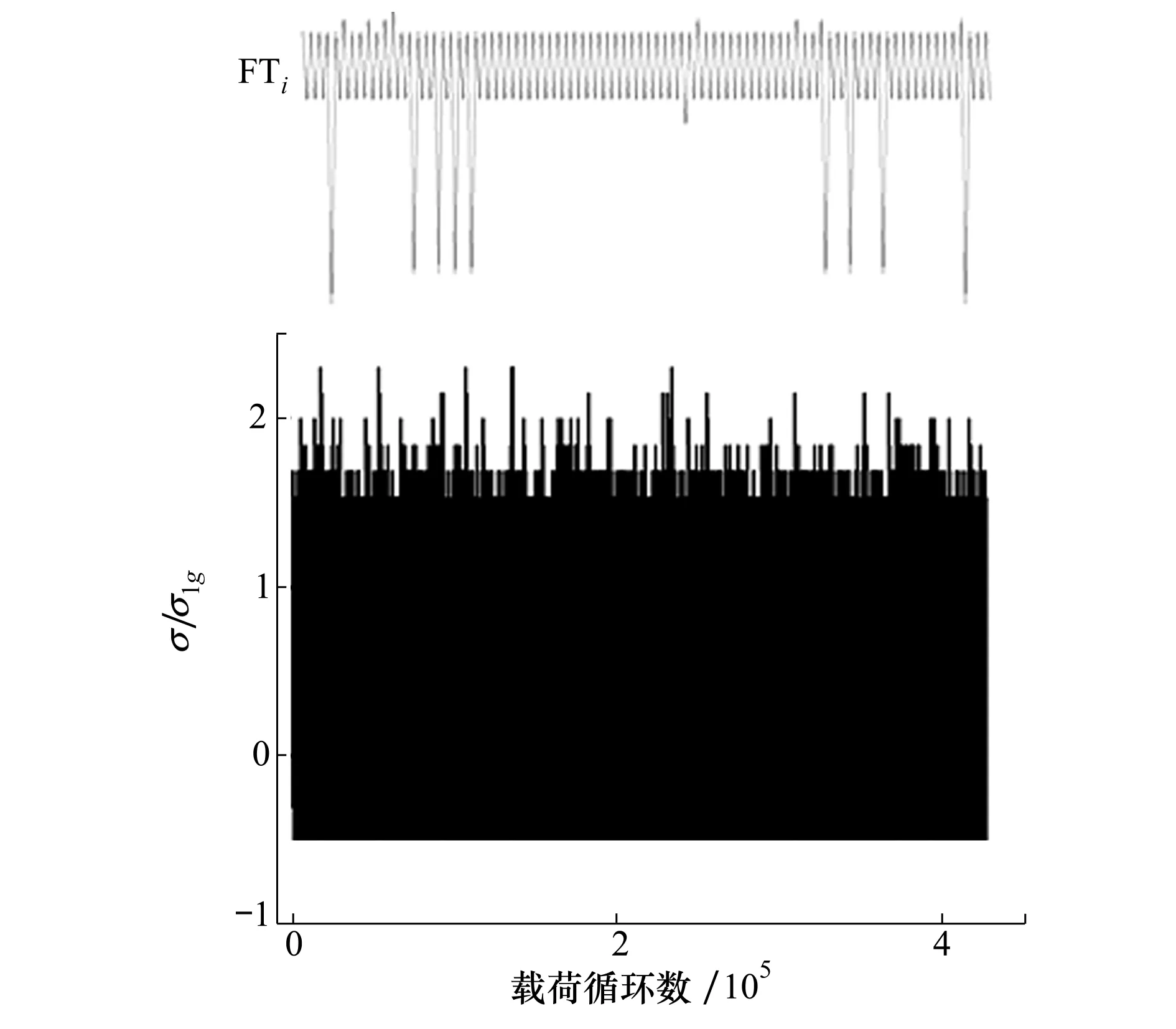
圖1 涉水結構模擬隨機載荷譜

1.3 Franc3D裂紋擴展分析

Franc3D軟件工作流程如圖2所示。

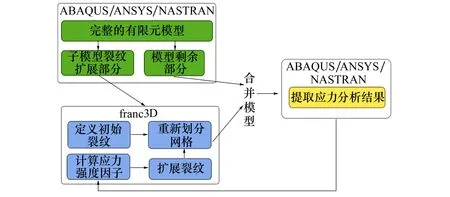
圖2 Franc3D工作流程

插入初始裂紋并重構網格后,Franc3D可以自動合并模型提交給有限元軟件進行計算,并提取應力計算結果,計算出3種開裂模式的強度因子。在設定好裂紋擴展步長后,軟件自動生成新的裂紋前緣并重新劃分網格,執行圖中所示的循環過程,直到裂紋擴展到特定的長度。

1.4 裂紋擴展壽命分析

隨機載荷譜中的超載作用后會使后續的低載的裂紋擴展速率減慢,即超載遲滯效應。常用的超載遲滯模型有Wheeler模型、等損傷模型、Willenborg/Chang模型等,其中Wheeler模型需要大量試驗參數支持,后2種模型對試驗參數要求低,在工程上更為常用。本文采用以殘余應力理論為基礎的Willenborg/Chang模型[14],其基礎為Walker公式

(2)

Willenborg/Chang模型裂紋擴展方程為

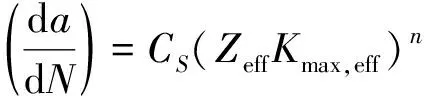
(3)

(4)

式中:Rcut為應力比截止值。

當后續載荷受到前置超載影響時,應力強度因子會減小,有效應力強度因子變為

(5)

Krs為前置超載而引起的殘余應力強度因子

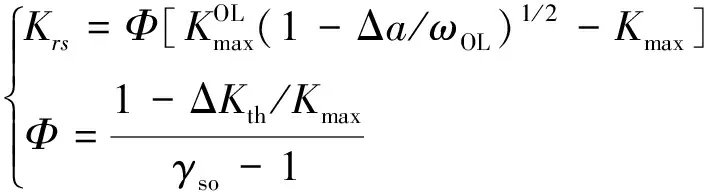
(6)

當Reff<0時,超載塑性區減小為有效超載塑性區,則

ωOL,eff=(1+Reff)ωOL

(7)

1.5 結構剩余強度分析

可以通過斷裂準則和凈截面屈服2種模式來確定結構的剩余強度。根據應力強度因子表達式,由斷裂準則可得結構剩余強度

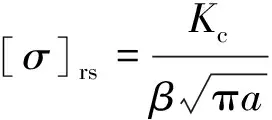
(8)

式中,Kc為斷裂韌度,構形因子β由(9)式確定

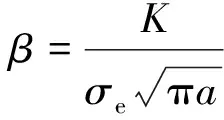
(9)

式中：K是應力強度因子；σe是遠端應力。于是剩余強度表達式轉換為

(10)

凈截面屈服準則公式為

(11)

式中:A凈為凈截面面積;A毛為毛截面面積;σys為材料的屈服強度。

1.6 檢查門檻值和檢查間隔

檢查門檻值是指從初始裂紋擴展至可檢裂紋尺寸的時間間隔再除以分散系數

(12)

式中:Fthr為到檢查門檻值的飛行次數;Finsp為檢查門檻值范圍,即從初始缺陷擴展至可檢裂紋尺寸的飛行次數。

檢查間隔為裂紋由可檢尺寸擴展至臨界尺寸的時間間隔除以分散系數

(13)

式中:Frep為重復檢查間隔的飛行次數;Fcrit為到臨界裂紋尺寸的飛行次數。

K1～K4分別為裂紋數據來源、載荷路徑、環境影響、不確定因素的分散系數。

2 涉水結構損傷容限案例分析

2.1 有限元建模

選取圖3所示某型水陸兩棲飛機某涉水框結構為對象,該框一側框緣有一截面為L型加強板,材料均為2024-T3鋁合金,E=72 400 MPa。加強板通過鉚釘與框結構連接,該結構一端固支,在另一端施加8 kN的拉伸載荷。

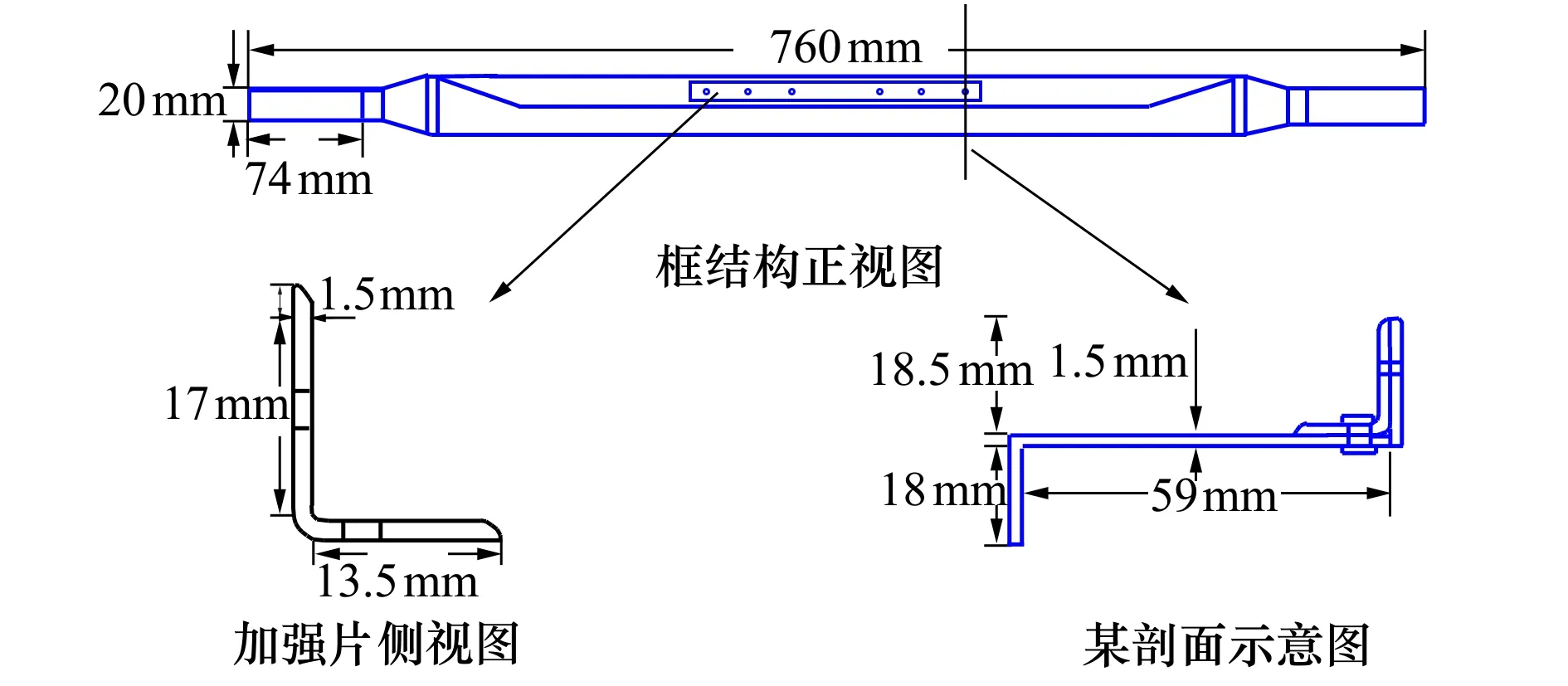
圖3 某涉水框結構幾何模型

為保證建模的準確性,須進行網格無關性檢驗。采取的策略是對鉚釘采用運動副建模,通過大幅改變全局單元尺寸,觀察最大應力的收斂情況[15]。

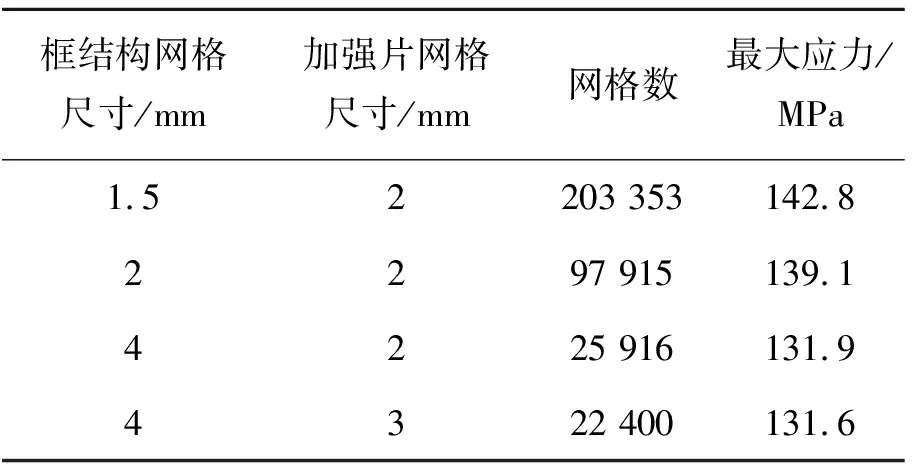
表3 最大應力隨網格尺寸變化情況

框結構和加強片網格尺寸分別為4,2 mm時最大應力收斂于131.9 MPa,且分析得到腹板最右側鉚釘孔處應力最大。運動副建模可以準確模擬鉚釘的載荷傳遞,但不能得到孔邊應力分布情況。在應力最大的鉚釘孔處添加實體鉚釘,建立有限元模型。對于遠離該孔的部位,網格可以適當放寬,但在鉚釘孔區域要對網格進行加密。最終在孔邊網格尺寸取0.1 mm時,孔邊最大應力收斂于215.5 MPa。模型一共有56 777個C3D8R網格。

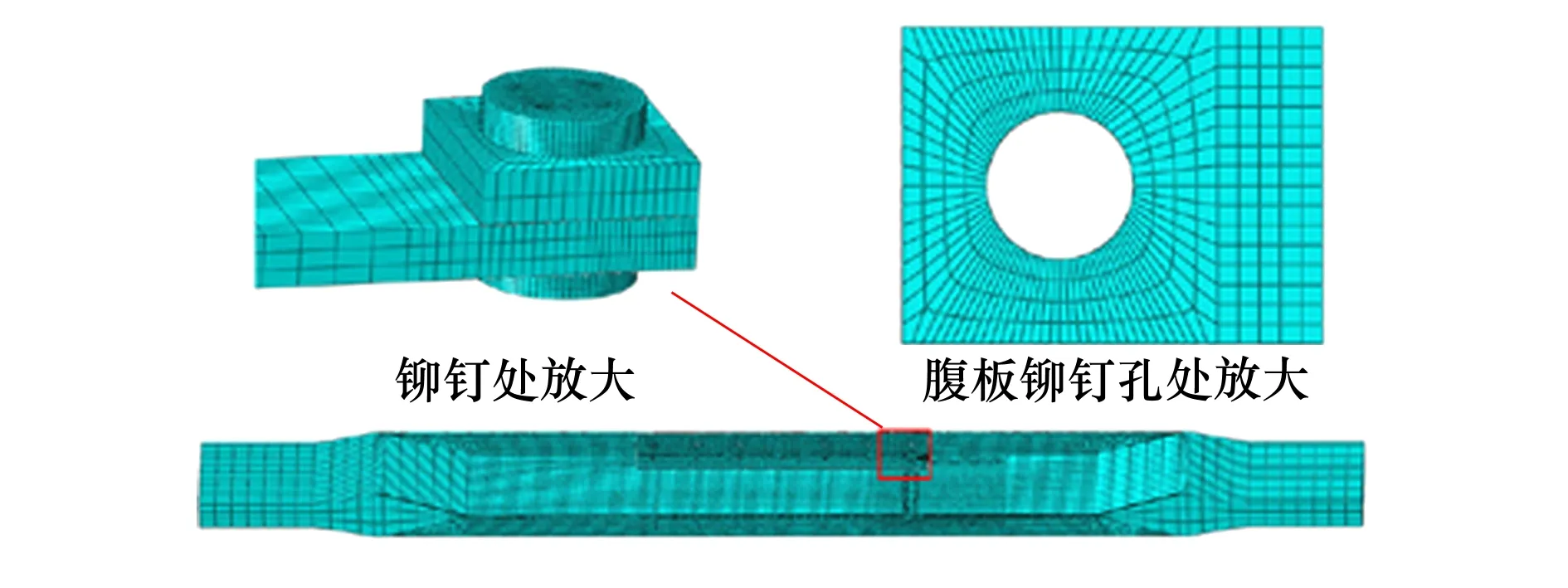
圖4 框結構有限元模型

圖5 鉚釘孔應力分布

計算得到鉚釘孔處應力分布如圖5所示。應力最大處為孔邊垂直于拉伸方向的位置,該位置為疲勞危險點。在進行裂紋擴展分析時,將該處作為裂紋初始位置。

2.2 裂紋擴展分析

沿垂直于拉伸載荷方向,將裂紋擴展區域剖分為子模型,根據《民機結構耐久性與損傷容限設計手冊》,該疲勞損傷危險點屬于典型連接孔的孔邊裂紋,故假設初始裂紋為1/4圓角裂紋,半徑為0.127 mm,子模型相對于整體模型位置及初始裂紋如圖6所示。假設該裂紋沿垂直于拉伸載荷方向,在腹板上擴展。

網格生成后軟件自動合并模型提交給ABAQUS計算,并提取應力分析結果,使用M積分計算應力強度因子。如圖7所示,將裂紋前緣坐標歸一化,兩端點坐標分別為0和1,其他各點坐標由其相對位置確定。計算得到初始裂紋的應力強度因子如圖8所示。

圖6 子模型及初始裂紋 圖7 裂紋前緣坐標歸一化 圖8 初始裂紋的應力強度因子

由圖8可以看出,在坐標為0處的KⅠ值較大,這是由孔邊應力集中造成的。KⅡ和KⅢ遠小于KⅠ,該裂紋為Ⅰ型張開裂紋。在裂紋擴展時選擇最大周向拉應力準則,由該準則裂紋擴展開裂角θ0為

(14)

裂紋擴展距離由用戶設定,將裂紋中點擴展距離設定為Δamid,則節點i的擴展距離為

(15)

式中,n為Walker公式中的參數。在計算出前緣各點擴展距離和開裂角后,得到各點的新坐標,對其進行擬合得到新的裂紋前緣。重新劃分網格進行計算,執行圖2中的循環過程。

裂紋經過18步擴展發展為穿透型裂紋,經過87步擴展后裂紋長度達到30.5 mm(投影至腹板表面的長度),各裂紋前緣如圖9所示。

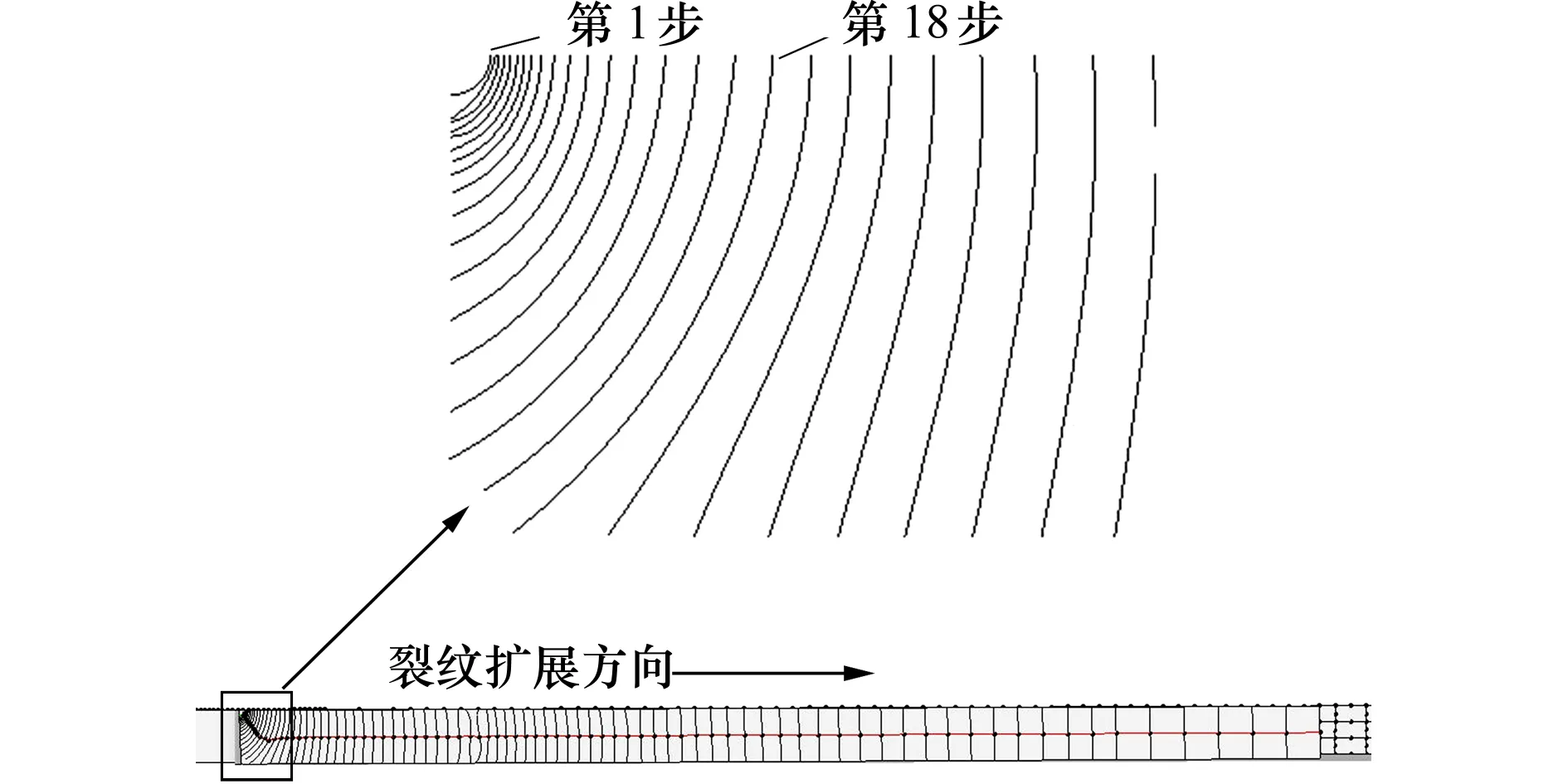
圖9 裂紋擴展裂紋前緣示意圖

分別取各裂紋前緣歸一化坐標為0,0.5,1處(即兩端和中點)的KⅠ值,形成應力強度因子曲線如圖10所示。

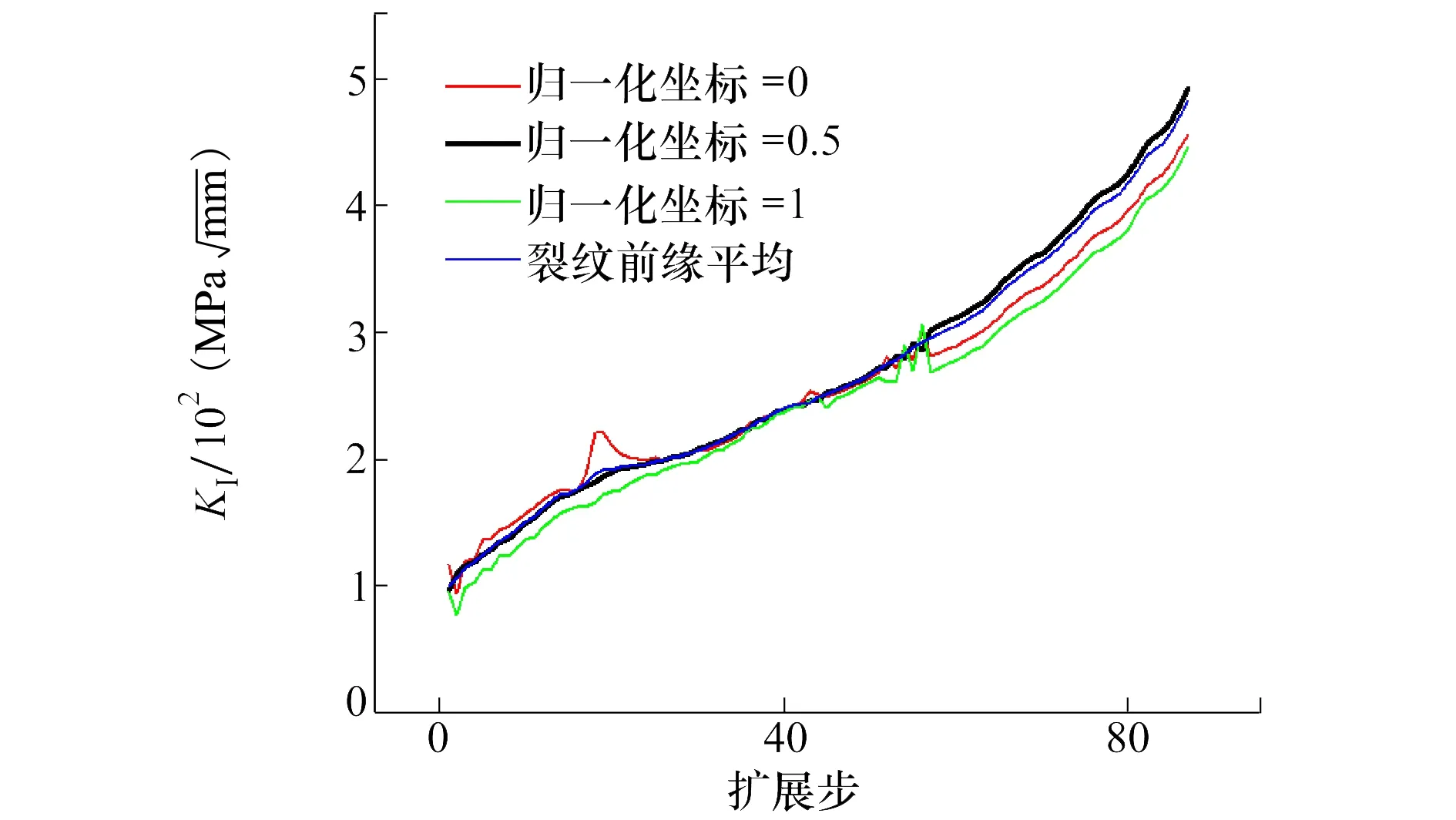
圖10 各裂紋前緣的應力強度因子曲線

在擴展步為18,即裂紋發展為穿透型裂紋時,坐標為0的曲線出現了一個峰值,這是由孔邊應力集中造成的。隨著裂紋擴展離開孔邊,該值逐漸下降,各裂紋前緣3個位置的KⅠ值較為接近。擴展步大于57時,中點的應力強度因子略大于兩端的值,但前緣平均值跟中點值較為接近。因此,選擇裂紋前緣中點的應力強度因子值進行裂紋擴展壽命計算。將各裂紋前緣中點擴展距離作為裂紋長度的表征。得到在8 kN拉伸載荷作用下,KⅠ與裂紋長度關系曲線如圖11所示。

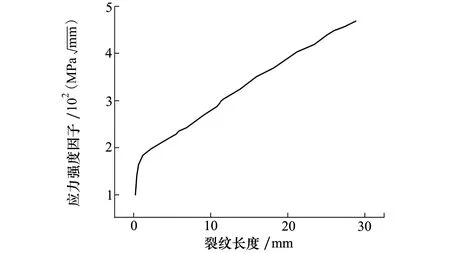
圖11 KⅠ隨裂紋長度變化曲線

2.3 裂紋擴展壽命計算

在利用Franc3D得到應力強度因子與裂紋長度關系后,使用Matlab編程計算裂紋擴展壽命。該程序流程圖12所示。

圖12 裂紋擴展壽命計算程序流程圖

程序自動讀取隨機載荷譜中每個循環的峰谷值,每個循環對應的應力強度因子值由(16)式決定

(16)

式中:K(a)為當前裂紋長度下,在8 kN拉伸載荷下的應力強度因子；P為載荷譜中的載荷乘數。

2024-T3鋁合金裂紋擴展參數[16]如表4所示。

表4 2024-T3鋁合金裂紋擴展參數

假設該框結構在海水浸泡、淡水浸泡及潮濕大氣暴露的時間比例分別為30%,30%,40%,由(1)式計算得到Cs為2.368×10-10。計算得到裂紋擴展壽命如圖13所示。

圖13 裂紋擴展壽命曲線

在假設的腐蝕環境中,如果不考慮載荷作用次序的影響,線性累加,利用Walker公式計算得到裂紋從0.127 mm擴展到30.87 mm,共經歷2 546次飛行;使用Willenborg/Chang模型計算飛行次數為2 924,超出前者14.8%。可見在使用隨機載荷譜進行裂紋擴展分析,計算裂紋擴展壽命時,必須考慮超載遲滯效應的影響,否則設計會偏于保守。而無腐蝕條件下,使用W/C模型計算得到壽命為4 490次飛行,腐蝕環境導致其壽命降低34.87%。

2.4 剩余強度分析

根據中國民航適航標準[17]相關規定,該結構剩余強度要求值為140 MPa。根據(9)、(11)式,可得剩余強度與裂紋長度關系如圖14所示。臨界裂紋長度為29.7 mm,對應的飛行次數為2 913次。

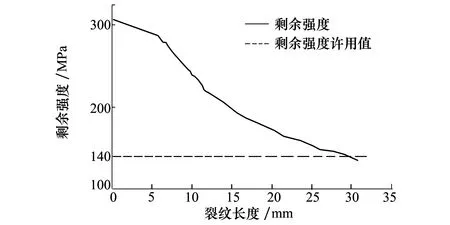
圖14 剩余強度-裂紋長度變化曲線

2.5 檢查門檻值和檢查間隔

該結構尺寸較小,不易目視檢查,故采取無損檢測中的滲透法進行檢測。查閱手冊[12]得到該檢測方法對該類結構可以檢測到的裂紋最小尺寸為6.35 mm,對應的飛行次數為2 137次。裂紋從最小可檢尺寸擴展到臨界尺寸共經歷776次飛行。對于該結構,根據手冊[12],K1～K4取值分別為2,3,1,1,則檢查門檻值和重復檢查間隔分散系數分別為2和3。由(12)～(13)式,得到檢查門檻值為1 068次飛行,檢查間隔為258次飛行。

3 結 論

對涉水結構進行損傷容限分析是保障水陸兩棲飛機飛行安全的重要組成部分。本文利用Franc3D和ABAQUS軟件聯合仿真,建立了腐蝕環境及包含水動力的隨機載荷共同作用下水陸兩棲飛機涉水結構件的損傷容限分析的工程方法。得出以下結論:

1) 在TWIST載荷譜上加入水動力沖擊對應的載荷水平及頻次,編制了涉水結構的模擬隨機載荷譜。

2) 某涉水框結構孔邊裂紋在腐蝕環、模擬隨機載荷譜共同作用下的裂紋擴展壽命為2 924次飛行,較不考慮超載遲滯效應的裂紋擴展壽命提高了14.8%,且腐蝕環境使其壽命大約降低34.87%。并確定其檢查門檻值、檢查間隔分別為1 068,258次飛行。

3) 以Franc3D計算結果為基礎進行二次開發,使用合適的裂紋擴展模型計算裂紋擴展壽命,可以滿足工程實際需求,本文分析方法同樣適用于實測的涉水結構載荷譜。

4) 通過本文結果說明,載荷作用次序對裂紋擴展壽命有較大的影響,在進行涉水結構損傷容限分析時必須考慮。此外,腐蝕環境對裂紋擴展壽命有顯著的降低作用,需要對涉水結構進行合理的腐蝕防護。