基于層次分析法-熵值法的軌道交通土建系統風險評價體系研究*

胡述筌 李海鋒 劉婉怡

(1.同濟大學道路與交通工程教育部重點實驗室， 201804， 上海； 2.上海市軌道交通結構耐久與系統安全重點實驗室， 201804， 上海； 3.同濟大學浙江學院交通運輸工程系, 314051， 嘉興； 4.上海市隧道工程軌道交通設計研究院, 200235, 上海∥第一作者， 碩士研究生)

為了制定軌道交通土建設施合理的養護作業計劃，需要評估各類傷損發生后的系統風險等級。目前針對軌道交通線路土建系統風險評估的相關研究較多，但大多僅對單一的橋梁[1]、隧道[2]、軌道[3]等設施進行風險評估，缺乏對各類設施整合的評價模型。若軌道、隧道、橋梁結構同時發生傷損，現有的風險評估體系無法判明這些病害對于整體運營風險的危害程度，也無法為其養護順序提供合理建議。

由于軌道交通線路上各設備的傷損數據性質不同，具有離散性質的指標(如鋼軌傷損等)的主要評價方式為扣分，具有連續性質的指標(如沉降量等)的主要評價方式為計算平均值、標準差等數學特征值。文獻[1-2]、文獻[4]對各種數據進行整合后，用以對土建設施的運營安全性進行評估，但這些研究對不同土建設施間的數據整合和風險分析仍較少。本文綜合考慮軌道、隧道、橋梁子結構中不同類別、不同性質的傷損指標，以期建立較為完善的適用于軌道交通土建系統的風險評價模型。

1 軌道交通土建系統的結構風險因素分析

目前部分軌道交通項目建有完善的土建系統傷損數據庫[5-6]，因此本文依照現有的設備檢查方式，直接采用這些數據庫中各類傷損的年度統計數據，并建立其風險評估體系。

如表1所示，軌道交通土建系統的風險評估體系在第一層次上分為軌道、隧道、橋梁3個評估子結構，各子結構下設第二層次的評估項目和第三層次的評估指標。

表1 軌道交通土建系統的風險評估體系指標Tab.1 Risk assessment system index of rail transit civil infrastructure system multivariate data fusion

本文采用的病害數據庫記錄了表1中各種設備病害、幾何形位改變、設備位移與沉降的頻次及程度。在此基礎上，本文參考了JGJ 8—2007《建筑變形測量規范》、GB 50157—2013《地鐵設計規范》、DB11/T 718—2016《城市軌道交通設施養護維修技術規范》、DG/TJ 08-109—2017《城市軌道交通設計規范》、GB/T 50299—2018《地下鐵道工程施工質量驗收標準》、CJJ/T 289—2018《城市軌道交通隧道結構養護技術標準》等規范，制定了相關的病害扣分標準。其中：橋梁與隧道沉降數據、隧道內徑變化的扣分標準需根據現場實際監測的數據變化趨勢進行調整，應將采集到的所有監測數據進行統計后，剔除其極端值，并取上四分位數作為扣分標準，建立了基于AHP(層次分析法)-熵權法的軌道交通土建系統風險評估體系。

2 AHP-熵權法風險分析體系建立

2.1 AHP-熵權法風險分析的計算流程

目前評估軌道交通土建設備系統的運營風險分析大多采用AHP及相關理論的延伸[7-9]，其優點為考慮了不同指標間評價基準的差異性，其缺點為不能充分描述評估指標間統計性質的差異性，易受主觀性影響等。若改為采用結合熵值計算權重的AHP進行分析，可充分考慮各評價指標的統計特征，相關文獻亦表明該方法具有較好的可靠性[10]。因此，本文建立了軌道交通土建系統的AHP-熵權法風險分析體系，其計算流程如圖1所示。

1)根據表1，參考相關規范制定設備的傷損扣分標準，并計算各層次評估項目和評估指標的權重。其中，第一層次不計算權重，3個子結構視為同等重要。

2)將第二層次評估項目、第三層次評估指標按其對土建系統安全性的影響進行排序，在參考專家意見后確定第二層次各評估項目的相對重要性，其權重值采用AHP進行計算。

3)第三層次評估指標采用綜合集成賦權法計算權重。對于具有連續性的評估指標，用熵值法提取相應的信息特征，最后取AHP、熵值法權重的加權平均數。

注：α——綜合集成賦權法中基于AHP的權重占比；ωh,i——i基于AHP的權重；ωh,ij——i下的j基于AHP的權重；ωe,ij——i下的j基于熵值法的權重；ωi——i的最終計算權重；ωij——j的最終計算權重。圖1 基于AHP-熵值法的軌道交通土建系統 風險體系計算流程Fig.1 Calculation process of rail transit civil infrastructure risk assessment system based on AHP-entropy method

4)評估指標的扣分值乘以對應的評估指標j權重ωij，再乘以該指標所對應的上一個層次評估項目i的權重ωi，可得到該評估指標的加權扣分值。將子結構內所有評估指標的加權扣分進行累加，可得到該子結構的加權扣分值，進而得到軌道交通土建系統的總扣分值，通過總扣分值的變化趨勢來評估該土建系統的風險等級。

2.2 權重計算

2.2.1 基于AHP的權重計算

AHP屬于主觀賦權法，其原理為將復雜的評估對象排列成遞階層次結構，對評估因素兩兩比較后給定相對重要性標度，并據此計算權重。本文中各評估因素相對重要性標度的確定采用比例標度法，其標度范圍為1～9。若i下的指標j比指標k極端重要，則標度為9；若指標j和指標k同等重要，則標度為1。相對重要性標度完成后，依照指標編號進行排序，分別建立對應的判斷矩陣A，并設同一層次項目對應的A為AI、同一層次指標對應的A為AF。按照式(1)～(6)，將AI轉換為量綱一化矩陣BI、AF轉換為量綱一化矩陣BF，并計算ωh,i及其特征值λi，以及ωh,ij及其特征值λij。

(1)

(2)

(3)

(4)

(5)

(6)

式中：

m——同一層級的評估項目總數；

aip——AI中第i行第p列的元素；

bip——BI中第i行和第p列的元素；

n——同一層次的評估指標總數；

ajk——AF中第j行第k列的元素；

bjk——BF中第j行第k列的元素。

由于相對重要性標度可能會相互矛盾，因此需進行一致性檢驗。若一致性檢驗未通過，需要重新調整相對重要性標度。可通過式(7)～(10)進行一致性檢驗。

(7)

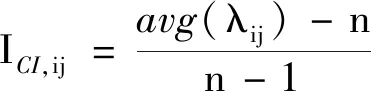
(8)

(9)

(10)

式中：

ICI,i——i對應的一致性指標；

ICI,ij——i下的j對應的一致性指標；

IRI,i——i對應的平均隨機一致性指標；

IRI,ij——i下的j對應的平均隨機一致性指標；

ICRR,i——i的一致性比值；

ICRR,ij——i下的j的一致性比值。

當ICRR,i<0.1時，代表對應判斷矩陣AI的不一致程度可接受，一致性檢驗通過。ICRR,ij判別方式亦同。

IRI,i和IRI,ij統稱為IRI，其取值可參照表2。將各評估項目判斷矩陣AI中所有特征值的平均值設為avg(λi)，各評估指標判斷矩陣AF所有特征值的平均值設為avg(λij)。avg(λi)和avg(λij)統稱為avg(λ)，ICI,i和ICI,ij統稱為ICI，ICRR,i和ICRR,ij統稱為ICRR，則基于AHP的權重檢驗結果如表3所示。

表2 不同m、n對應的IRI值Tab.2 IRI values with different m,n

表3 基于AHP的權重檢驗結果Tab.3 Inspection result of weight values based on AHP method

2.2.2 基于熵值法的權重計算

熵值法屬于客觀賦權法，其原理為通過計算熵值來判斷各指標的離散程度。離散程度越大，則該指標對綜合評價的影響越大。該法可充分利用數據的統計特征，具有較高的精確度，但對樣本的依賴性比較大，若無豐富現場工務經驗的專家或技術人員對權重值的設定進行指導，可能會導致熵值法權重計算結果無法真實反映評估指標的重要性。因此，本文僅使用熵值法對第三層中具有數據連續性的評估指標進行權重計算，如隧道結構沉降A2-B2-C2、A2-B2-C3、A2-B2-C4及A2-B3-C5，以及橋梁結構沉降B2下的評估指標A3-B2-C2、A3-B2-C3。

2.2.2.1 去除極端值

為了減少極端數據對熵計算的影響，在參考現場調研報告后，確定篩選極端值準則為：若單一樣本的數據值在整體數據求和后總值中的占比超過20%，則該數據值被視為極端值并去除。此外，去除極端值的樣本總數需不高于樣本總數的2%。

2.2.2.2 數據標準化

熵值需要進行對數計算，故在去除極端值后參照式(11)采用臨界值法將數據進行標準化。

(11)

式中：

xj——原始評估指標j的監測數據集；

xj,l——監測數據集xj內的第l個數據；

yj,l——去除極端值后的評估指標j數據集yj內的第l個數據。

2.2.2.3 熵值計算

將去除了極端值后的標準化數據集代入式(12)～(13)，可計算得到ωe,ij。

(12)

(13)

式中：

L——yj,l去除極端值后的樣本總數；

Hj——評估指標j對應的熵值。

2.2.3 最終計算權重確定

根據上文AHP、熵值法計算得到的權重結果，第二層次各評估項目最終計算權重ωi直接采用AHP權重，第三層次各評估指標最終計算權重ωij利用綜合集成賦權法進行計算。其計算式如圖1所示。

本文以現有軌道交通土建系統的數據標定熵值法權重，并結合樣本數據可信度情況和專家建議，確定α取0.4，最終得到的權重計算結果如表4～5所示。

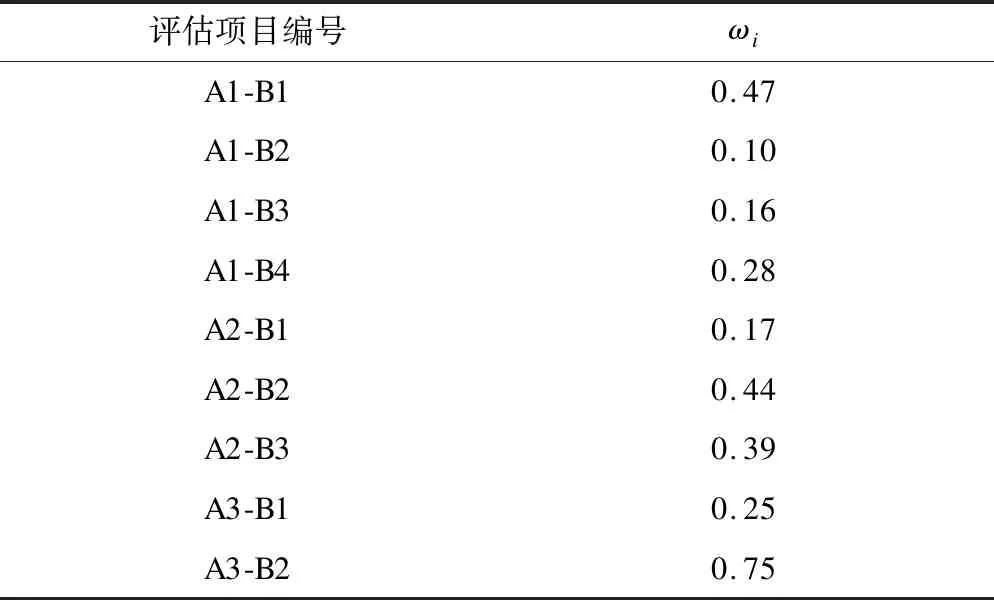
表4 第二層次各評估項目的最終計算權重Tab.4 Final calculated weight values of second layer assessment items

3 軌道交通土建系統風險評估體系的應用案例分析

本文以某地鐵線路2013年、2016年的檢測數據為例，利用上文構建的軌道交通土建系統風險評估體系對這兩個年度的風險趨勢變化進行分析。將該線路分為3個區段，各區段的長度及需評估的子結構如表6所示。

表5 第三層次各評估指標的最終計算權重Tab.5 Final calculated weight values of third layer assessment index

表6 評估案例線路各區段長度及涵蓋的子結構Tab.6 Length and substructure of assessment case line sections

將3個區段內各區間子結構第二層次評估項目、第三層次評估指標進行扣分，分別乘以相應的權重后再進行求和，最終得到各區間各類子結構的風險評估加權總扣分值，其計算式為：

(14)

式中：

Ds——某個區間子結構s的加權總扣分；

ds,ij——子結構s下的評估項目i評估指標j的扣分值。

基于得到的總扣分值劃分各區段線路區間的風險等級。 參照現有評估規范，本文的風險等級劃分按照以下原則實施：各線路區段按扣分情況將線路區間劃分為Ⅲ級、Ⅱ級、Ⅰ級。其中：①Ⅲ級區間為風險評估加權總扣分不小于40分或單項評估子結構的扣分大于25分的評估區間；②Ⅱ級區間為風險評估總扣分小于40分且不小于25分的評估區間；③Ⅰ級區間為風險評估總扣分小于25分的評估區間。

該線路各區間的風險評估結果如圖2所示。由圖2可以看出，該線橋梁區段的風險源主要來自于軌道子結構，其加權扣分值也高于隧道區段軌道子結構的加權扣分值；隧道區段的風險源則較平均。由此可知，橋梁區段應針對軌道子結構強化監控、養護作業，隧道區段的軌道子結構、隧道子結構皆應強化監控、養護作業。

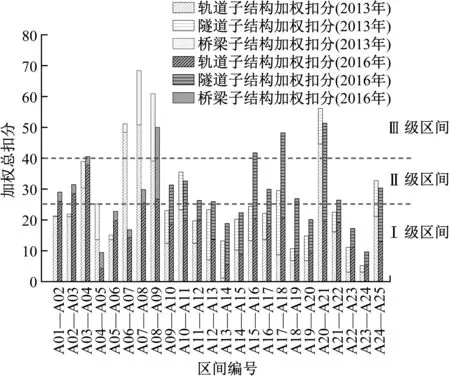
圖2 案例線路各線路區間的風險評估結果(2013年、2016年)Fig.2 Risk assessment result of case line intervals in 2013 and 2016

如表7所示，對該線路2013年、2016年Ⅲ級、Ⅱ級、Ⅰ級區間個數進行統計后可知：2013年Ⅰ級區間的占比為62.5%，2016年Ⅰ級區間的占比下降至33.3%；Ⅲ級區間的占比則由2013年的20.8%上升到2016年的33.3%。這表明了在常年運營下，該線土建系統的風險有逐年升高的趨勢，建議強化全線的養護作業。

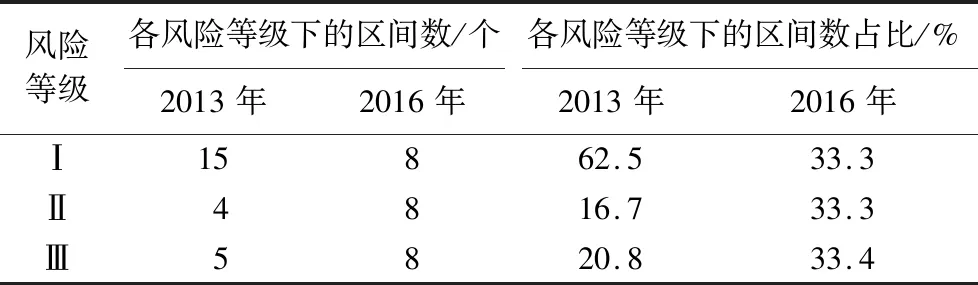
表7 案例線路區間的風險等級統計(2013年、2016年)Tab.7 Statical result of case line intervals at different risk grades in 2013 and 2016

4 結語

本文所建立的軌道交通土建系統風險評估模型可同時用于評估軌道、隧道、橋梁等線路土建設施的運營風險。結合現有的工務設備傷損扣分標準及線路上的監測數據，先以AHP量化專家群確定的不同傷損類別相對重要性并計算得到主觀權重，再以熵值法將線路上連續監測數據轉化為部分評估指標的客觀權重，最后結合兩者的計算結果，采用綜合集成賦權法計算出各評估項目和評估指標的最終權重。

采用本文提出的風險評價模型對案例線路進行整體風險評估，比對案例線路評估期間土建設施性能惡化的具體狀況，提出了相應的養護建議。對案例線路的應用分析結果表明，該評估體系具有一定的合理性和工程可用性，可為其他軌道交通項目土建系統的運營安全風險評估提供參考。