基于改進模擬退火算法的火焰溫度場反演計算

王 旭，祝海江*，劉興旺，李小春

(1. 北京化工大學信息科學與技術學院，北京 100029；2. 中國電子科技集團公司第四十一研究所，山東 青島 266555)

1 引言

燃燒著的高溫火焰經常出現在工業、軍事等生產過程中，比如冶金行業中的窯爐，飛機、火箭等航空航天項目燃料推進的尾焰，包括炮彈爆炸所造成的高溫火焰等。因此，在技術不斷迭代更新的過程中，溫度場分布逐漸成為了工業生產、科學研究中的一項重要參數指標。從通過儀器接觸火焰的接觸式測溫，到非接觸式測溫；從對溫度場的單點測溫，到對溫度場區域進行分布測量，溫度測量領域有了極大的發展。接觸式測溫法雖然不受環境中其它因素的干擾，且測量方式較為簡便，但對于高溫火焰卻無法有效的測量。

本文采用非接觸式測溫法中輻射圖像的方法進行火焰溫度測量。該方法通過像機對待測蠟燭火焰圖像進行采集，從而進行溫度場測量。通過簡單的線性函數關系將圖像灰度值轉化為溫度值。通過縱向反演計算，即將圖像上每一像素點的縱向溫度區域劃分為多段溫度并通過普朗克定律進行計算，可將對溫度場進行分布測量的問題轉化為對一組函數方程求解最優值的問題。對于最優化問題，采用模擬退火算法進行求解。在模擬退火算法進行計算前，需要認為設置算法的初始參數。但由于迭代一次退火算法時間較長，若不斷人工設置參數，對比計算效果，使得過程很是繁瑣，因此需要采用自動調參的方法對模擬退火算法進行進一步的改進。超參數調優的方法包括了：網格搜索法、隨即搜索法、貝葉斯優化等方法。網格搜索法相對簡單，通過計算搜索范圍內的所有網格點確定最優值，但該方法在需要調優參數較多時十分消耗計算時間和資源；隨機搜索法與網格搜索法較為相似，是在搜索范圍內隨機選取樣本點，進行最優值計算；貝葉斯優化的方法與前兩者不同，其會利用之前數據點計算后得到的信息，從而提升最優值的求解速度。

針對模擬退火算法進行溫度場重建時，會面臨手動調整參數過程較為繁瑣、耗時過長等問題。本文給出了一種基于超參數優化的溫度場縱向反演法重建方法，該方法利用貝葉斯優化(Bayesian Optimization)，實現了模擬退火算法中的參數自動尋優，快速找到最優解。這種對模擬退火算法中參數自動優化的方法能夠減少算法的計算成本，極大地提高計算效率。基于改進后的模擬退火算法對火焰溫度場進行縱向反演計算，得到火焰不同區域的火焰溫度分布。

2 本文方法

2.1 基于模擬退火算法的溫度場縱向反演法重建

溫度場縱向反演法是在已知火焰輻射圖像的灰度值與溫度或輻射強度之間的函數關系的情況下，將其代入普朗克定律中，對火焰輻射圖像上的各個像素點進行反演計算。

(1)

一般的火焰滿足上述條件，可采用簡化的普朗克定律進行計算。假設將CCD像機拍攝的火焰二維圖像上的每個像素點縱向上的溫度劃分為多個區域，即

T

…

T

，通過上式可知，縱向上的單色輻射強度為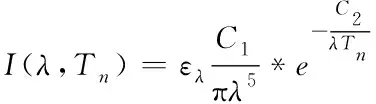

(2)

在經過不同波長的濾光后，每一像素點的總輻射強度可表示為：

I

(

λ

，

T

)=

I

(

λ

，

T

)+…+

I

(

λ

，

T

)

(3)

因此，通過上述方程可將溫度場重建過程轉換為求解最優解的數學問題：

?

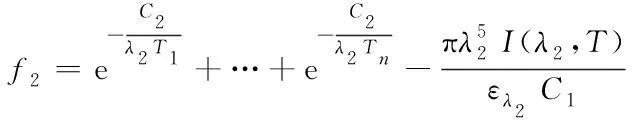
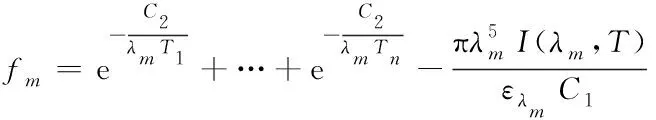
(4)

同時，在

T

={

T

…

T

}的條件下，對下式取最小值。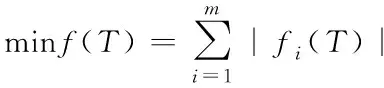

(5)

模擬退火算法能夠很好的解決局部最優解的問題，并且模擬退火算法作為一種隨機優化算法，能夠較快地找到最優化問題的近似最優解。該算法在求解的過程中會以一定的概率接受一個效果不是十分理想的解，從而有可能跳出局部最優解，達到全局最優解。

綜上所述，基于模擬退火算法的溫度場縱向反演法重建方法歸納如下：

1)假定所選取的初始溫度

T

，退火溫度最終值為

T

；每一溫度下的迭代次數為

L

，溫度下降速率為

alpha

，當前模型的退火值為

T

=

T

*

alpha

并定義初始溫度模型

S

，即將縱向溫度分為三段溫度，目標判定函數為式(5)。2)對

S

的三個溫度值施加隨機的擾動，擾動方向依據擾動點在三維空間中的位置信息計算得出

d

={

d

，

d

，

d

}(

d

=-1，1，0)，跨度Δ

S

，

S

=[

T

+Δ

S

*

d

，

T

+Δ

S

*

d

，

T

+Δ

S

*

d

]，Δ

f

=

f

(

S

+1)-

f

(

S

) 。

4)在同一退火溫度下，迭代

L

次。

5)重復迭代，直至滿足退火算法的收斂要求。

在采用模擬退火算法進行溫度場重建時，諸如退火算法初始溫度

T

，每一溫度迭代次數

L

等超參數均需要在退火算法運行前進行人工設置，但在超參數的溫度重建結果未知的情況下，手動調整參數的方式顯然較為繁瑣，耗時過長。因此，對于這一類無法隨著模型的迭代而不斷優化的參數，需要通過自動優化的方法來減少算法的計算成本。

2.2 基于貝葉斯優化的溫度場縱向反演法重建方法

針對上述問題，本文研究了一種基于超參數優化的火焰溫度場縱向反演重建方法，該方法能夠實現模擬退火算法中的參數自動尋優，快速找到最優解。相比于其它自動超參數調優方法，貝葉斯優化(Bayesian Optimization)充分利用了上一個點的信息，找到下一個測試的點，從而快速到達最優解。因此，本文給出了一種基于貝葉斯優化的溫度場縱向反演重建方法。

貝葉斯優化主要包含兩個核心部分：概率代理模型(Probabilistic Surrogate Model)和采集函數(Acquisition Function，AC)。貝葉斯優化本質上更偏向于減少評估的代價，使得優化的過程能夠經過較少次數的評估得到最優解。在每次迭代的過程中，算法都會對采集函數的最大值的數據點即最有“潛力”的點進行評估，最終收斂到最優解。

概率代理模型是采用一個概率模型來代理目標函數

f

(

x

)，而高斯過程則是較為常用的一種模型。高斯過程(Gaussian processes， GP)可視為多元高斯概率分布的范化。一個高斯過程由均值函數

μ

和協方差函數組成。其中均值函數

μ

(

x

)=

E

[

f

(

x

)]，協方差函數

k

(

x

，

x

′)=

E

{[

f

(

x

)-

μ

(

x

)][

f

(

x

′)-

μ

(

x

′)]}，通常設置

μ

(

x

)=0。給定訓練數據

x

，…

x

，其對應的函數值為

y

，…

y

，組成樣本點集

D

={(

x

1：，

y

1：)}。首先假定數據提前被中心化，即函數滿足

f

(

x

)～

GP

(0，

K

)，其中

(6)

對于新樣本

x

+1來說，它會更新高斯過程的協方差矩陣

k

=[

k

(

x

+1，

x

)，…，

k

(

x

+1，

x

)]

(7)

協方差矩陣更新為：

(8)

通過更新后的協方差矩陣以及前面的樣本可估計出

f

+1的預測分布：

P

(

f

+1│

D

1：，

x

+1)～

N

(

μ

，

σ

)

(9)

(10)

σ

=

k

(

x

+1，

x

+1)-

k

K

k

(11)

由于高斯過程本身有陷入局部最優的問題，因此需要通過采集函數來尋找下一個最優值，采集函數的目的在于平衡探索(exploration)和利用(exploitation)兩者的選擇。“探索”目的在于盡量選擇遠離已知樣本點的數據點用作下一次迭代；“利用”目的在于盡量選擇接近已知樣本點的數據點用作下一次迭代。常用的采集函數有UCB(Upper confidence bound)、PI(Probability of improvement)、EI(Expected improvement)三種，本文采用UCB，

UCB

=

μ

(

x

)+

kappa

*

σ

(

x

)

(12)

kappa為調節參數，可理解為上置信邊界。

在溫度重建過程中，模擬退火算法中存在初始溫度T、溫度下降速率alpha、最終溫度T和每一溫度迭代次數L這四個不因迭代而發生變化的超參數。考慮到最終溫度T本身的值設定的較小以及alpha為一小于1的小數，因此，對T和L這兩個超參數通過貝葉斯優化方法進行超參數調優，從而達到更好的溫度場重建效果。

在進行參數調優前，算法會在T和L兩個超參數的值的范圍內隨機選擇一定數量的數據點作為樣本點，進行模型訓練。隨后，利用高斯過程回歸的方法求解未知點的均值與方差，未知點的數值范圍與已知點相同。利用采集函數(本文選用UCB的采集函數)找到貝葉斯優化猜測的最大值的點，即采集函數值最大的點。觀察所得出的猜測的點對應的最大函數值是否符合要求。不符合要求則繼續進行下一次的高斯過程回歸和采集函數的求解。本文基于貝葉斯優化的溫度場縱向反演法重建方法的算法框圖如圖1所示。

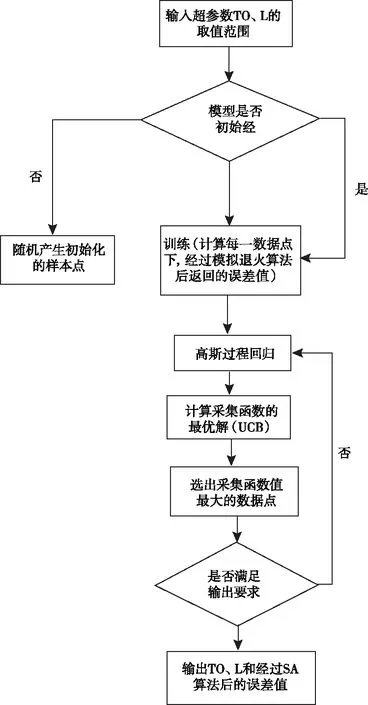
圖1 基于貝葉斯優化的溫度場縱向反演法重建方法的算法框圖

3 實驗結果與分析

3.1 本文方法的驗證實驗

通過像機對蠟燭火焰進行拍攝，并分離出R、G、B的灰度值。采用簡單的線性函數關系將圖像灰度值轉化為溫度值。由于蠟燭的火焰周圍的光影會影響溫度的測量以及減少模擬退火算法的迅速按成本，對蠟燭的火焰圖像進行邊緣檢測，只對邊緣檢測后輪廓內部的數據采用退火算法進行計算。每個像素點的退火運算結束后，得到的誤差值存儲至誤差矩陣中，并相加得出全部參與計算像素點的誤差和作為一次模擬退火算法的誤差值。

設定最終溫度

T

=10，

alpha

=0

.

98，并對退火算法的兩個超參數

T

、

L

進行賦值。設定溫度初始溫度

T

=2500，每一溫度迭代次數

L

=100，進行退火運算。同時設置初始溫度

T

=3000，迭代次數

L

=200，再次進行退火計算，并比較二者的誤差值，觀察退火算法得到的誤差對實際重建溫度計算時的影響。火焰輻射圖像中每個像素點通過退火算法會產生該像素點的計算誤差，并將其相加作為一組超參數下退火算法的計算誤差，如式(5)。如下為兩組超參數的三段溫度的重建結果，X和Y分別代表火焰圖像的寬和高。

圖2 改進后的三段溫度重建結果(T0=3000，L=200)

由圖2可知，改進后的誤差更小的重建結果火焰底部與上部區分較為明顯，而圖3未改進的結果底部與上部的數值區分不夠明顯，這表明圖2的重建結果更能明顯地展現溫度值的變化，也更符合通過灰度值轉換成溫度后的溫度矩陣的數值分布情況。

圖3 改進前三段的溫度重建結果(T0=2500，L=100)

3.2 貝葉斯優化與網格搜索的實驗比較

網格搜索是一種簡單的參數優化方法，其本質是將待優化超參數在空間中按照一定范圍劃分為大小相同的網格，每一點可代表一組超參數的值。通過對范圍內的所有數據點進行計算，對比所求出的結果，進而得出性能最佳的一組超參數值。當設定范圍足夠大，且參數步長較小時，這種窮舉的方法能夠找出全局最優解。但劃分的網格內，大部分的點準確率并不能達到要求，且網格搜索需要遍歷所有的數據點，這無疑會產生許多不必要的運算，從而增加計算的時間成本。在考慮到模擬退火算法迭代一次后的運算時長較長，因此網格搜索無法高效的完成對退火算法的超參數調優任務。反之采用貝葉斯優化的方法則能夠以較短的時間求解出誤差較小的一組超參數。

對退火算法的兩個超參數T、L進行自動的參數調優。首先采用網格搜索的方法，設定溫度初始溫度T數據范圍為[2500，3000]，步長為100；每一溫度迭代次數L數據范圍為[100，200]，步長為50。結果如圖4所示。

采用貝葉斯優化進行參數調優，超參數范圍與上述實驗相同。由于貝葉斯優化器在選取超參數的數據點時是連續的，因此在將超參數輸入到退火算法時，對T、L進行取證操作，避免小數的出現。經過貝葉斯優化器進行參數調優后，結果如圖5、圖6所示。

圖4 網格搜索結果

圖5 貝葉斯優化初始點

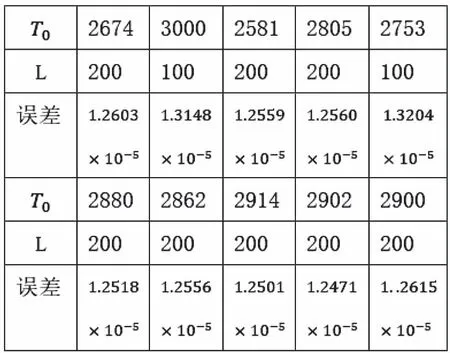
圖6 貝葉斯優化數據

由圖4可知，經過網格搜索后，發現當L=200時要比L=[100，150]誤差更小。但是在采用網格搜索的過程中，超參數L=[100，150]時進行的退火運算次數較多，使得參數調優的效率下降。由表2可知，貝葉斯優化的方法在經過前5次初始參數點的計算后，可知L=200是較為合適的參數值，并在參數優化的過程中(如表3所示)，將更加關注超參數T的優化，這大大降低了參數優化所需時間，并最終得出參數優化的結果，表明[2902，200]是誤差較小的一組超參數。兩種優化方法中，有4組數據在超參數相同的情況下，得到了不同的誤差結果。這是由于退火算法本身屬于一種依靠概率求解的算法，因此，在采用相同超參數時，兩次計算的結果會有所差異。但二者差異較小，不影響參數優化過程。

與網格搜索相比，網格搜索能夠在所選取的網格點找到誤差的近似最小值，但在僅知道參數范圍的情況下，想提高網格搜索的精度，必然要縮小搜索步長，這會極大提高超參數優化方法的運算成本。貝葉斯最優化與網格搜索不同，在進行優化時，會采用前一個參數點的數據信息(均值μ和方差σ)。因此，對于模擬退火算法這種運算量較大的方法時，貝葉斯優化顯然能夠極大地提高優化速率。

4 結論

本文對采集到的火焰圖像數據通過模擬退火算法進行溫度反演計算，從而重建溫度場。并通過貝葉斯優化改進退火算法，自動優化退火算法中的超參數，同時對比了網格搜索法的優化效果。實驗結果表明，貝葉斯優化方法能夠極大減少對退火算法進行超參數優化的運算成本。

致謝：

感謝裝備預先研究項目一般基金(61400030202)對本文工作的資助。