基于鄧肯-張模型鋼筒倉糧食貯料側壓力仿真

靜 行，王曉雨，陳慧芳

(河南工業大學土木工程學院，河南 鄭州 450001)

1 引言

筒倉作為各種貯料儲藏的特種結構，具有容量大、造價低、節約用地、綠色環保等優點，已廣泛應用于糧食、煤炭、化工等眾多領域之中。由于貯料本身具有復雜的力學特性，儲存過程中貯料與筒倉之間的相互作用更為復雜，影響筒倉結構的受力性能。其中，倉內貯料產生的側壓力是筒倉結構受到的主要荷載，由其導致的筒倉結構開裂、倒塌會引發嚴重后果。因此，確定筒倉倉壁側壓力是筒倉結構分析與設計的基礎，關乎結構安全性與經濟性，對于完善糧食貯料鋼板筒倉結構體系的相關理論和設計方法具有重要意義。

目前，國內外學者主要利用理論計算、試驗分析和數值模擬三種手段對貯料倉壁側壓力分布規律展開研究。理論分析方法主要有Janssen理論、Airy理論、Reimbert理論和Jenike理論等方法，這些理論均基于一定的假設條件，理論求解結果與實際數據會產生差別。另外，貯料與筒倉側壁的相互作用具有不確定性，試驗分析易受儀器精度、試驗方案等多方面因素的影響，而有限元等數值模擬方法發展也愈加成熟，其計算精度被廣大研究者接受，因此，眾多研究者將有限元分析方法應用于貯料壓力分析之中。Mahmoud等采用非線性雙曲型本構方程和有限元方法，估算了彈性波紋板圓形筒倉倉壁靜壓力；Ayuge等運用ANSYS模擬靜、動態不同單元類型的兩種模型，提出了一種新的筒倉流量分析方法；Martinez等服從Drucker-Prager屈服準則和Mohr-Coulomb模型進行有限元模擬，計算出筒倉靜態以及中心卸料過程中的受力性能與側壓力分布；劉震等通過對筒倉靜態及卸料狀態的模擬，發現最大倉壁靜壓力出現在筒壁與漏斗的過渡部分，卸料時倉壁動態側壓力遠大于靜態側壓力；楊鴻等采用Drucker-Prager屈服準則反映貯料的本構關系，借助數值模擬探究了貯料在靜、動態作用下對平底倉及錐底倉倉壁的側壓力分布規律，分別討論了貯料的剪脹性、泊松比、彈性模量、膨脹角等參數對倉壁側壓力的影響。糧食貯料對本構模型的適用性不盡相同，倉內貯料選擇合理的本構模型與數值模擬計算結果的精確度密切相關。文獻[14]引入鄧肯-張模型描述直剪試驗下豆粕的剪切變形特性，對模型中各彈性參數的適用性進行分析，模擬結果與試驗結果擬合效果理想；文獻[15]將鄧肯-張(E-B)本構模型植入FLAC二次開發，利用由小麥三軸試驗求取的模型參數，進行高大平房倉糧堆底部壓力數值模擬。上述文獻研究表明鄧肯-張本構模型可以用于糧食力學特性相關模擬分析。

為準確計算糧食對筒倉倉壁的靜態側壓力，驗證鄧肯-張(E-B)本構模型的適用性，基于ABAQUS有限元軟件二次開發建立三維筒倉模型，通過模擬實倉靜態側壓力來驗證小麥鄧肯-張(E-B)本構模型的適用性，進而研究了不同高徑比鋼筒倉貯料側壓力的分布規律，并將分析結果與中、美、歐三國筒倉設計規范進行對比分析，為貯料側壓力計算和鋼板筒倉結構設計提供理論方法和參考依據。

2 有限元模型分析

2.1 糧食貯料的本構關系

E-B本構模型是在土體等散體材料中被廣泛采用的一種非線性本構模型。模型采用雙曲線方程表示材料三軸試驗(

σ

-

σ

)～

ε

曲線，即

(1)

式中，

σ

、

σ

分別為三軸壓縮試驗的最大、最小主應力；(

σ

-

σ

)為偏應力；

ε

為軸向應變；

a

、

b

為試驗常數，由試驗數據確定。

一定應力狀態下，其切線模量、初始切線模量分別按照下式進行計算

(2)

(3)

式(1)中圍壓

σ

通常為常數，對式(1)進行微分，當

ε

→0雙曲線的初始切線模量

E

又可表示為

(4)

當

ε

→∞時，可由式(1)求得偏應力漸進值(

σ

-

σ

)

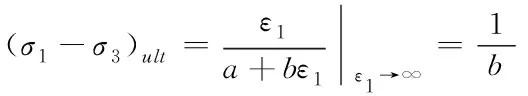
(5)

可見，

a

為初始切線模量

E

的倒數，

b

為偏應力漸進值(

σ

-

σ

)的倒數。

切線體積模量與圍壓的關系可表示為

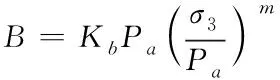
(6)

卸載時，假定卸載模量

E

僅隨

σ

變化，不與(

σ

-

σ

)有關。

(7)

式中：

K

為初始模量系數；

n

為初始模量指數；

P

為大氣壓，取101

kPa

；

R

為破壞應力比；

c

、

φ

分別為貯料的粘聚力和內摩擦角；

K

為體積模量系數；

m

為體積模量指數；

K

為卸載模量系數，一般

K

=1

.

5～3

.

0

K

。

2.2 鄧肯-張(E-B)本構模型的合理性驗證

為驗證E-B本構模型的適用性，建立文獻[17]中實際鋼筋混凝土淺圓倉的有限元模型。該淺圓倉倉身直徑28m，高36m，高徑比為1.3，糧倉示意圖如圖1(a)所示，在測點1～7處布置壓力盒用于測試貯料側壓力。有限元模型中，糧食貯料的材料屬性采用E-B本構模型，模型參數見表1；鋼筋混凝土倉體材料屬性與文獻[17]一致；壓力測試的裝糧高度取13.5m和17.6m兩種情況，有限元模型如圖1(b)所示。運用有限元模型計算不同裝糧高度的貯料側壓力，并將計算結果與現場實測數據進行對比分析，結果如圖2所示。

由圖2中可以發現，不同裝糧高度測點1～7位置處的側壓力有限元分析結果與現場實測結果吻合較好，分布趨勢基本一致，最大偏差(絕對)值不超過10%，由此表明用有限元方法分析筒倉貯料側壓力是可行的，且E-B本構模型適用于描述小麥貯料的材料屬性。出現偏差的原因主要是小麥貯料材料屬性采用本文中E-B本構模型參數，與文獻[17]中小麥材料屬性有所區別，進而導致兩者結果出現偏差。

圖1 淺圓倉示意圖及有限元模型

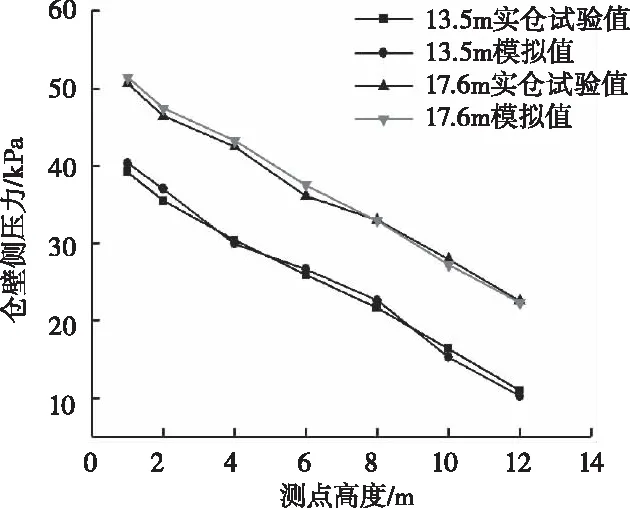
圖2 筒倉倉壁側壓力實測值與模擬值對比

表1 小麥貯料E-B模型參數值

2.3 糧食鋼板筒倉模型建立

建立淺倉(

H/D

=1

.

2)和深倉(

H/D

=2)兩種有限元模型，分析靜態作用下糧食貯料側壓力。淺倉高6

m

，深倉高10

m

，直徑均為5

m

，壁厚均為0

.

01

m

。鋼板筒倉彈性模量206

Gpa

，密度7850

kg/m

，泊松比0

.

3；小麥貯料參數見表1，其中小麥對鋼板筒倉有效摩擦系數為0

.

3。有限元模型中，鋼板筒倉采用殼體單元

S

4

R

，小麥貯料采用實體單元

C

3

D

8

R

。圖3為淺倉模型中小麥貯料與筒倉倉體的網格劃分，殼單元與實體單元表面網格劃分一致。模擬過程中糧食貯料與鋼板筒倉采用剛柔接觸和面面接觸方式，選擇剛度大的面(筒倉的內壁、底部)為主面，剛度小的面(糧食貯料的側壁、底部)為從面。接觸面間的相互作用包含接觸面之間的法向作用與切向作用，在法向作用中保持默認“硬接觸”，切向作用中設置貯料對筒倉的摩擦系數為0

.

3。因重力為數值模擬的唯一外荷載，故僅施加豎直方向上的重力加速度9

.

8

m/s

，筒倉底部完全固結，糧食貯料底部約束其豎向位移。

圖3 淺倉有限元模型網格劃分

2.4 糧食貯料壓力分析

通過上述數值模擬分析，貯料在重力荷載作用下位移分布云圖如圖4所示，倉內貯料

Mises

應力分布云圖如圖5所示，倉壁與貯料接觸應力分布云圖如圖6所示。由圖4可知，僅考慮重力作用下，小麥貯料均出現均勻沉降，沿倉壁逐漸減小，頂部沉降量最大。其中，淺倉頂部沉降量達到11

.

9

mm

，深倉頂部沉降量達到29

.

8

mm

。由圖5可知，貯料內部的最大應力位于底部，且靠近倉壁附近貯料應力大，遠離倉壁的中間區域應力小，同一水平面的應力呈非均勻分布。隨著裝糧高度增加，貯料底部壓力增大。圖6可以看出，因荷載與結構均具有軸對稱性，倉壁側壓力分布呈對稱且均勻分布。靜置儲糧狀態下，沿計算深度的增大，倉內小麥貯料與倉壁間側壓力呈逐漸增大趨勢。深倉與淺倉最大側壓力均出現于筒倉底部附近，這與文獻[11]、[18]數值模擬結果規律基本一致。

圖4 貯料位移響應云圖

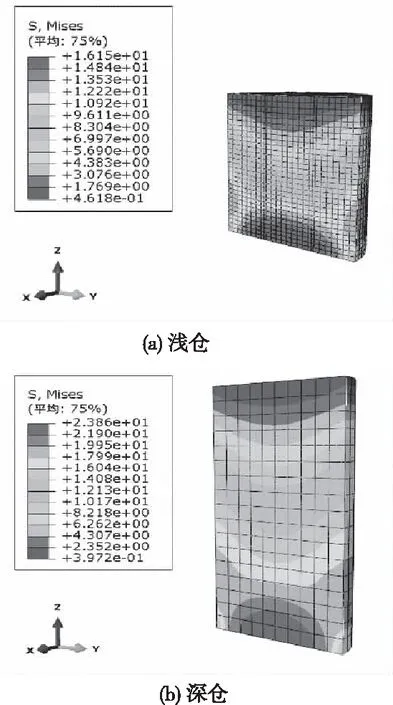
圖5 貯料等效應力分布云圖

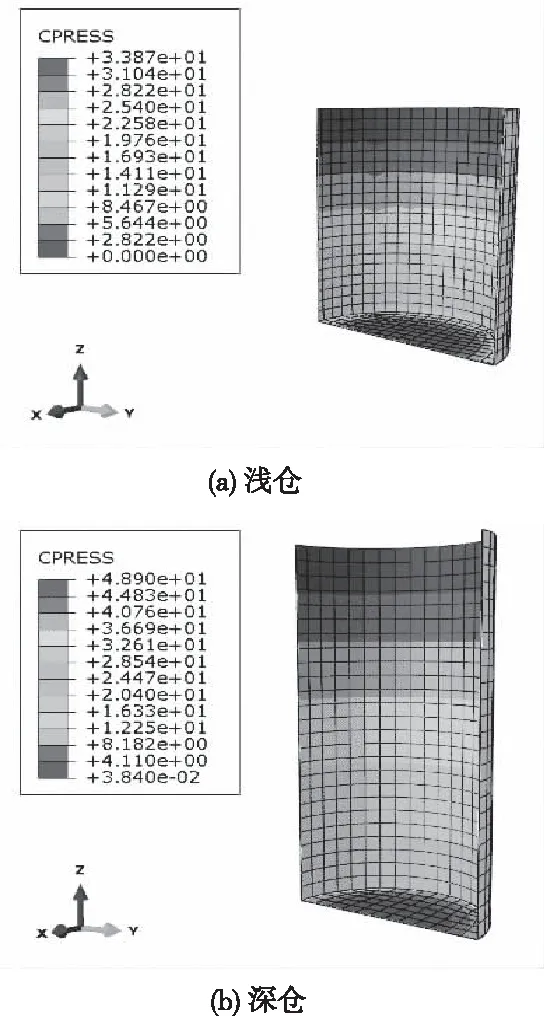
圖6 倉壁接觸應力分布云圖

3 數值模擬結果與各國糧食筒倉設計規范對比

目前，中、美、歐等國家相關規范中在貯料對筒倉設計靜態側壓力計算方面大多采用

Janssen

公式，各國根據國家經濟基礎、設計要求等實際情況基于

Janssen

公式進行修正，部分參數計算存在差異。對于深倉側壓力的計算，各國規范基于

Janssen

公式，采用不同側壓力系數。對于淺倉側壓力的計算，中國規范認為深倉與淺倉的邊界條件不同，基于

Rankine

理論提出了淺倉計算方法；美國、歐洲規范中沒有明確區分深倉與淺倉，采用同深倉一樣的壓力荷載計算方法。

3.1 中國規范[19]：

3

.

1

.

1 深倉在計算深度

s

處，作用于倉壁單位面積上的水平壓力標準值按式(8)計算

(8)

3

.

1

.

2 淺倉

在計算深度s處，作用于倉壁單位面積上的水平壓力標準值按式(9)計算

P

=

kγs

(9)

其中：k=

tan

(45°-φ/2)為側壓力系數，γ為貯料重力密度，μ為有效摩擦系數，ρ為筒倉凈截面水力半徑。

3.2 美國規范[20]

歐洲、美國規范中計算方法同

Janssen

理論，且無深、淺倉之分，區別在于側壓比系數計算方法不同。深度

Y

處的水平壓力

P

=

kq

(10)

深度Y處的豎向壓力

(11)

式中：側壓力系數k=1-

sin

φ；R為筒倉橫截面的水力半徑。

3.3 歐洲規范[21]：

歐洲規范考慮了中心裝料與偏心裝料對筒倉貯料側壓力的影響，對于中心裝料筒倉貯料側壓力計算，

任意深度z處，貯料對倉壁水平壓力

P

=

P

Y

(

z

)

(12)

其中

P

=

γkz

(13)

Y

(

z

)=1-e-

(14)

(15)

式中：側壓力系數k=1.1(1-

sin

φ)，z為倉壁底面處至儲糧頂面的深度，A為筒倉橫截面的截面積，U為筒倉橫截面周長。將數值模擬結果同中、歐、美三國規范對比分析，其筒倉沿倉壁深度的靜態側壓力分布如圖7所示。由圖可知：無論深倉與淺倉，小麥貯料的數值模擬結果與我國規范側壓力計算值沿倉壁變化趨勢較為接近，進一步驗證了筒倉側壓力有限元數值模擬的可行性。對于深倉，中、歐、美規范均基于

Janssen

理論，中國規范比歐、美規范更接近數值模擬結果。最大側壓力出現在筒倉底部附近，此處三種規范計算值偏差較大，分析原因主要是采用了不同側壓力系數，由此導致側壓力值偏差過大。對于淺倉，中國規范采用

Rankine

理論計算側壓力，歐、美規范仍采用

Janssen

理論，因此，中國規范側壓力變化趨勢與歐美兩國規范值有所區別；倉壁側壓力模擬值與我國規范較為吻合，歐、美規范因采用較大側壓力系數導致側壓力計算值偏大，且三國規范計算值均大于數值模擬結果；在鋼筒倉上部，靜態側壓力模擬值與我國規范值差距小，中下部差距大。可見歐、美規范無論深倉、淺倉均基于

Janssen

理論且將側壓力系數考慮過大導致設計分析結果偏于保守。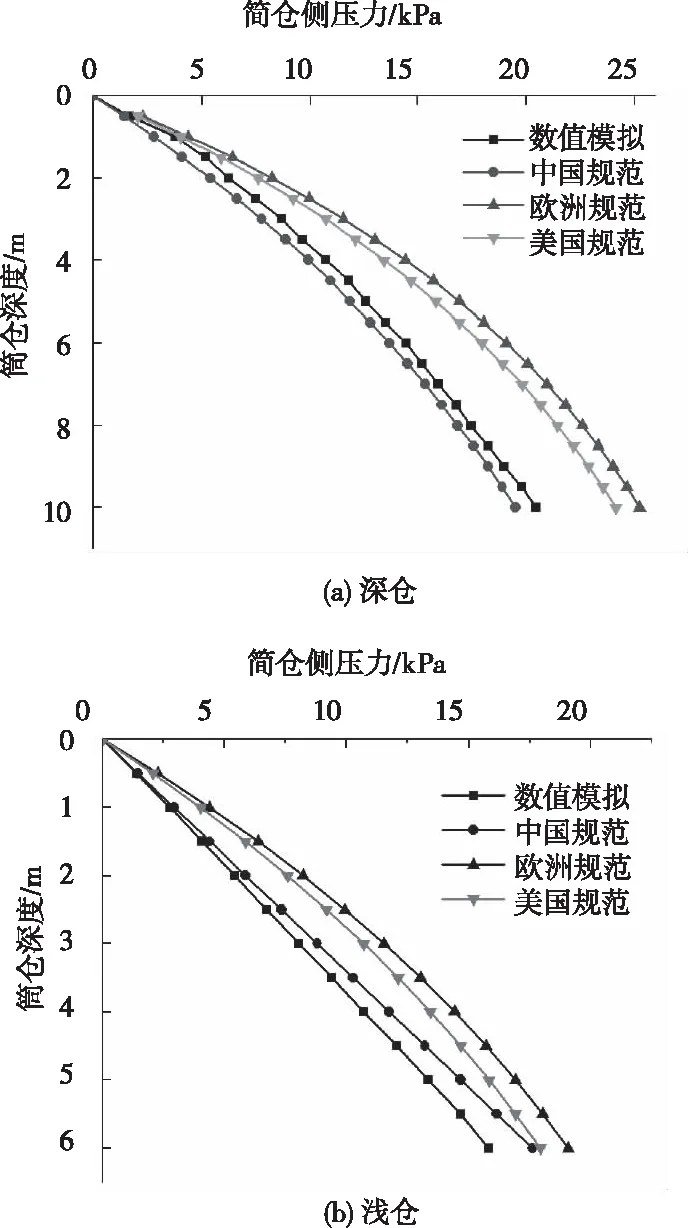

圖7 小麥貯料鋼板筒倉靜態側壓力分布

4 結論

本文采用鄧肯-張(

E

-

B

)本構模型描述小麥貯料的材料屬性，基于

ABAQUS

有限元軟件二次開發建立三維筒倉模型，進行了實倉測試結果的模擬驗證，研究了不同高徑比鋼筒倉貯料側壓力的分布規律，并將數值模擬結果與中、美、歐三國筒倉設計規范進行對比分析，得出以下結論：1)實際鋼筋混凝土淺圓倉數值模擬結果與實測試驗數據吻合良好，表明了采用鄧肯-張(

E

-

B

)本構模型能夠較好的描述小麥糧食貯料的材料屬性，同時表明筒倉側壓力有限元分析方法的有效性。

2)儲糧靜置狀態下鋼筒倉貯料側壓力沿筒倉深度增加，逐漸增大，深倉與淺倉最大側壓力均位于筒倉底部附近；貯料內部的最大應力位于底部，且靠近倉壁附近貯料應力大，遠離倉壁的中間區域應力小，同一水平面的應力呈非均勻分布。

3)不同高徑比鋼筒倉倉壁側壓力模擬值與各國規范計算值分布規律基本一致，說明數值模擬可以正確反映筒倉受力情況；數值模擬結果與中國規范計算值更為接近，歐美兩國規范因側壓力系數取值過大導致側壓力偏大。