基于馬氏決策的5G網絡切片虛擬資源分配研究

曾堅毅，許濟金

(1. 福州理工學院，福建 福州 350506；2. 福建農林大學機電工程學院，福建 福州 350002)

1 引言

隨著5G網絡的快速發展，各大網絡運營商需要通過有限的物理資源為用戶提供不同的定制服務，這便造成了通信業務不斷擴大的局面，由此產生了網絡切片技術。傳統網絡切片技術在資源調度和利用方面存在諸多不合理之處，尤其當用戶需求突增的情況下，用戶的服務保障會受到較大影響。為了解決網絡切片資源在時間與空間的整體利用率問題，保障網絡運行商收益和高質量用戶體驗，不少學者針對網絡切片資源的部署、運營和調度等問題進行研究。

文獻[2]將用戶中斷概率、切片隊列積壓和切片總速率作為約束條件和回報，建立資源自適應動態優化模型，通過自適應虛擬資源分配算法與外界環境不斷交互，對資源分配進行調整，從而優化切片的性能。該方法可以提高系統性能，但切片的時延性有待提高。文獻[3]通過SDN技術對網絡切片資源進行自適應分配，完成虛擬資源的調度，并根據資源的屬性分類及網絡聚類結果，優化資源分配，該方法在分配網絡切片資源的過程中具有較好地自適應性，但分辨能力較差。文獻[4]將最大化平均切片與速度作為目標，建立隨機優化模型，并引入PDS概念對系統轉移概率進行優化，使系統可以根據當前狀態為每個網絡切片分配合適的資源，該方法大大降低了網絡寬帶的壓力，但該算法針對狀態空間維數較大的情況需進一步研究。

基于以上研究，針對網絡切片虛擬資源的分配問題，本文提出基于馬氏決策的5G網絡切片虛擬資源分配方法。根據檢測的切片信息對虛擬資源進行分配，對5G網絡切片虛擬資源存儲結構進行設計與異構有向分析，構建虛擬資源節點分布模型，最終求解出5G網絡系統的最大長期收益。

2 5G網絡切片模型

2.1 調度模型

為了使5G網絡能夠充分利用資源、滿足超高寬帶的需求。通過對網絡切片調度模型的建立，為用戶定制最佳的虛擬資源分配方案。在系統中，假設有

A

個網絡切片，每個網絡切片擁有

K

個用戶，并支持

A

種類型的不同業務。在時間

T

內，根據檢測的切片信息對虛擬資源進行分配。假設在時刻

t

時用戶數為

B

(

t

)，則它可表示為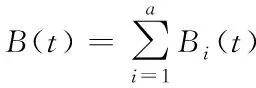

(1)

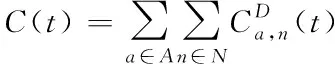
(2)

2.2 用戶速率

系統中整個信道均服從瑞利衰落模型，信道中的噪聲為高斯白噪聲。假設切片

a

所接入的資源模塊具有同一個子載波

b

的用戶為

k

，，網絡總發射功率為

E

，則功率

E

可表示為

(3)

其中，

e

，表示子載波

b

的用戶分配功率。在鏈路中，子載波

b

的用戶接收信號可表示為

x

，=

f

，

D

+

δ

，

(4)

其中，

f

，表示子載波

b

從基站到接收端信道的系數；

δ

，表示子載波

b

的噪聲。由香農公式可知，子載波

b

的用戶

i

對應速率可表示為

(5)

其中，

G

表示子載波

b

的帶寬；

H

，表示用戶

i

的干擾噪聲比。假設切片

a

總共接入子載波集合為

J

，那么切片的總速率可表示為

(6)

3 虛擬資源分配

3.1 虛擬資源模型

為了實現對5

G

網絡切片虛擬資源分配，首先對5

G

網絡切片虛擬資源存儲結構進行設計與異構有向分析。構建虛擬資源節點分布模型。對鏈路模型中接入網絡切片資源分配的相關性采取提取調度，通過聯絡特征分析方法對虛擬資源分配的特征集進行構建，網絡切片虛擬資源的相對貼近度用公式可表示為

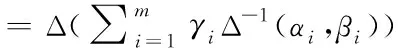
(7)

其中，

φ

表示虛擬資源的相對貼近度；(

α

，

β

)，…，(

α

，

β

)表示5

G

網絡切片虛擬資源的特征分布集；

γ

表示虛擬資源的權重系數。建立5

G

網絡切片虛擬資源的分析模型，對接入系統的網絡切片資源進行統計分析，采用雙饋入的特征模擬方法對虛擬資源分配進行加權融合，并對虛擬資源的相似度信息進行描述。假設5

G

網絡切片虛擬資源數據集為

Y

={

y

，

y

，…，

y

}，

m

為虛擬資源分配目標的個數，

Y

為虛擬資源分布特征點，可以采用均值聚類的方法對虛擬資源網絡屬性進行識別。

3.2 虛擬資源特征

在異構有向圖分析方法的基礎上，結合特征空間重組技術對虛擬資源結構進行構建，對虛擬資源進行優化設計，5

G

網絡切片虛擬資源的約束參數用公式可表示為

(8)

在負反饋環節，對網絡中接入的信號進行控制，建立網絡信道的均衡模型，對虛擬資源進行相關性分析，得出5

G

網絡切片虛擬資源的調度模型，用公式可表示為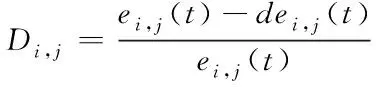

(9)

依據共享度水平，對網絡中接入的切片資源進行構建，得出網絡切片虛擬資源的分配模型，用公式可表示為

(10)

根據網絡中接入系統的虛擬資源定量評價模型的描述，可以得出子系統網絡線輸出的評價集，用公式可表示為

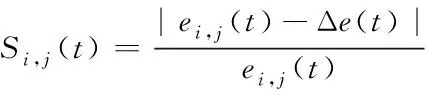
(11)

進而可求出5G網絡切片虛擬資源的均值聚類最優解，用公式可表示為

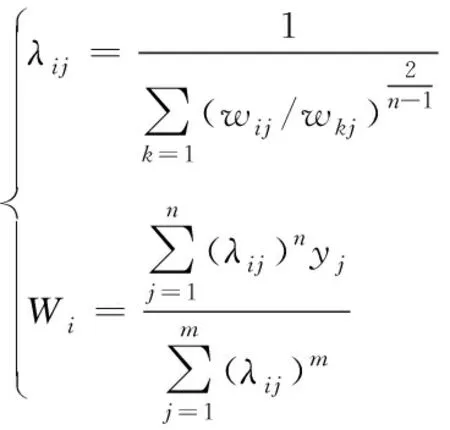
(12)

根據提出的最優聚類分析方法，結合特征空間重組技術對虛擬資源的結構進行重組，并對虛擬資源的相關特征變量進行提取，有利于提高資源分配能力。

4 馬氏決策

馬氏決策是順序決策的經典形式，也是一種理想化的數學形式。基于馬氏決策，本文建立5G網絡切片資源管理模型，結合貝爾曼方程及馬氏決策過程的動態規劃求解運營商最優收益解和網絡資源利用率。

馬氏決策過程主要通過構建問題來實現目標，其中學習者和決策者稱為代理，與代理交互或者代理之外的事物稱為環境。在每個時間步長

t

內，代理會接收到環境的狀態

S

＿，并對其作出相應的動作

A

＿。在下一個步長內，代理便取得收益

R

＿+1，并取得新的狀態

S

＿+1。馬氏決策過程產生的序列用公式可表示為

S

＿0，

A

＿0，

R

＿1，

S

＿1，

A

＿1，…

(13)

馬氏決策過程產生的狀態、動作以及收益都是有限的，離散的概率分布受到前一個隨機狀態和動作的影響，在

t

時刻離散的隨機概率用公式可表示為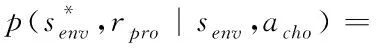

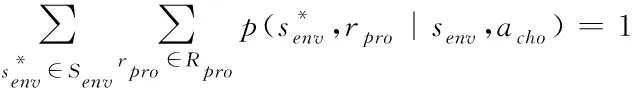
(14)

(15)

進而期望收益用公式可表示為

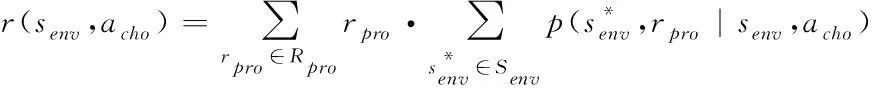
(16)

代理獲得的收益由它采取的動作決定，這種動作行為稱為策略。若代理在

t

時刻執行的策略為

ξ

，那么在狀態

S

＿=

s

時所執行策略

A

＿=

a

的概率為

ξ

(

a

|

s

)，預期收益函數用公式可表示為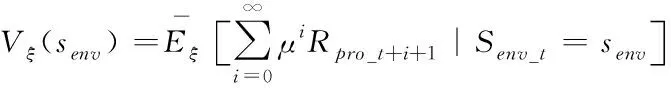

(17)

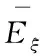
(18)

其中，

μ

表示折扣率，在狀態

s

下采取策略

ξ

時的策略函數用公式可表示為

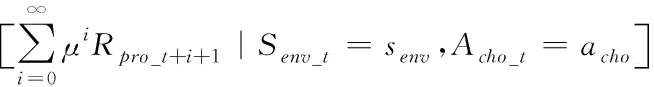
(19)

在馬氏決策過程中值函數具有遞歸特性，因此對于任何狀態和策略，在下面的狀態值時，會保持一致性，狀態值公式可表示為

(20)

通過迭代計算，可以求出下一個狀態的收益值函數，這便是卡爾曼方程。在卡爾曼方程中通過對事件的概率進行加權可以把事件的可能性平均化，對于有限的馬氏決策過程，可以對最優策略進行準確描述。若預期收益

V

(

s

)≥

V

(

s

)，那么有策略

ξ

≥

ξ

，若最優策略為

ξ

，由最優策略可求出最優值函數，公式可表示為

(21)

最優策略的動作值函數可表示為

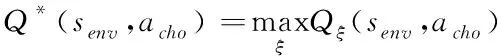
(22)

考慮到5

G

網絡資源的管理特性，管理策略的選擇很有可能導致網絡運行商的收益受到影響，所以通過馬氏決策過程的動態規劃算法求出最優值函數和最優策略函數，同時求出運營商長期收益的最優解，公式表示為

(23)

綜上所述，求出的解就是5G網絡系統的最大長期收益。

5 仿真與結果分析

為了驗證基于馬氏決策的5G網絡切片模型的準確性，本文設置不同的參數分析網絡切片資源分配系統的性能。假設5G網絡由4個VRU組成，并且每個網絡切片服務有2個VRU，為了驗證收益值的最優解，將本文提出的方法與傳統網絡資源分配方法進行對比。實驗在Matlab仿真軟件上進行，通過不同參數值的設置，隨機重復100次實驗，得到切片資源管理的最大收益值對比結果如圖1所示。

圖1 切片服務到達率與最大累積收益的關系

從圖中可以看出，隨著切片服務到達速率的增加，5G系統長期最大收益不斷增加，在新切片請求增加時，采用本文提出的馬氏決策5G網絡資源分配方法能夠保證系統具有充足的資源來處理切片請求，服務協議中的每一個策略均使收益值達到最優狀態。

將5G系統資源VRU作為變量，通過增加虛擬資源塊的個數，測試系統最大收益，仿真對比結果如圖2所示。

圖2 VRU數量與最大累積收益的關系

從圖中可以看出，當虛擬資源塊個數較少時，兩種方法求出的累積收益值相近，隨著虛擬資源塊個數的增加，本文方法明顯優于傳統方法，傳統方法每次都會為切片請求分配最大的VRU，導致資源利用率較低，使系統長期收益不理想。

保持實驗參數不變，得到最大長期累積收益值與切片服務離開率之間的關系，結果如圖3所示。

圖3 切片服務離開率與最大累積收益的關系

從圖中可看出，隨著切片離開率的增加，5G系統最大長期累積收益也不斷增加，當離開率為10時，累積收益最大。隨著離開率的繼續增加，由于新切片請求到達率一定，切片服務離開率會增大到極限值，使5G系統的處理速率超出預定值，導致過多的資源處于等待狀態，因此累積收益會不斷降低，通過仿真可以看出采用本文算法的累積收益明顯優于傳統方法，具有一定的實用性。

最后通過仿真比較兩種方法在相同切片服務請求到達率情況下的服務阻塞率，以及本文方法在不同切片服務請求離開率下的切片服務阻塞率變化情況，結果如圖4和圖5所示。

圖4 兩種方法阻塞率對比結果

圖5 本文方法在不同離開率下的阻塞率變化

從圖中可以看出，隨著切片服務請求到達率的增加，切片的阻塞率不斷增加，而且采用本文方法的阻塞率明顯低于傳統方法。通過不同切片服務離開率的對比結果可知，隨著切片服務離開率的增加，系統服務單位時間內可允許接入的切片增多，因此切片的阻塞率明顯降低。然而當切片服務請求到達率達到20時，阻塞率將保持穩定狀態，由于系統到達了服務處理的極限能力，因此5G網絡系統會通知阻止切片的到達服務請求。

6 結束語

對于虛擬資源分配問題，本文提出一種基于馬氏決策的5G網絡切片管理模型。通過對網絡切片調度模型的建立，為用戶定制最佳的虛擬資源分配方案，基于馬爾科夫決策理論對虛擬資源進行建模，分別對系統轉移函數、狀態值以及網絡運營商的收益進行分析。為了驗證基于馬氏決策的5G網絡切片資源分配模型的準確性，在Matlab軟件上進行仿真，設定5G網絡由4個VRU組成，并且每個網絡切片服務有2個VRU。實驗結果表明，采用本文方法后，無論VRU與切片服務如何變化，5G網絡運行商的長期累積收益均得到顯著改善，且切片的阻塞率呈現明顯降低趨勢。