車輛狀態與參數聯合估計研究

姬 曉，李 剛，2，樊東升

(1. 遼寧工業大學汽車與交通工程學院，遼寧 錦州 121001；2. 吉林大學汽車仿真與控制國家重點實驗室，吉林 長春 130025)

1 引言

在當今社會所倡導的低碳與零排放發展趨勢下，推廣電動汽車取代傳統燃油車已經成為近幾年汽車行業轉型的有效手段之一。而分布式驅動電動汽車又作為電動汽車重要發展方向之一，為汽車在主動安全控制及穩定性控制等方面帶來了顯著的優勢。汽車關鍵狀態與參數變量的準確獲取是進行車輛主動安全控制以及穩定性控制的前提。但針對這些重要參數變量的估計研究普遍采用算法模型估計器，算法模型中車輛自身的一些參數(如質量、轉動慣量和質心位置等)以及路面附著系數通常直接采用固定值，在對車輛行駛狀態估計的過程中大多忽略這些參數變化的影響。此外在汽車行駛的過程中，由于工況的不斷變化，導致這些參數變量也隨之不斷發生改變，從而影響汽車行駛狀態估計的準確性。因此，在車輛行駛狀態估計的過程中同時考慮車輛自身參數以及路面附著系數的變化就顯得尤為重要。文獻[4]采用單一擴展卡爾曼濾波理論的狀態與參數估計框架，實現了對車輛運動狀態的實時估計，但未實現對其它參數的估計。文獻[5]將單輪胎滑移控制模型與擴展卡爾曼濾波器結合估計車輛的運動狀態、路面附著系數、車輪滑移率和質量參數，但無法使用足夠的信息來計算協方差矩陣，有待調整和改善。文獻[6]基于改進的Sage-Husa自適應擴展卡爾曼濾波理論對車輛的行駛狀態進行估計，提高了算法的魯棒性。文獻[7]考慮路面附著系數的影響，將平方根容積卡爾曼濾波算法與多模型交互算法進行融合，提高了車輛狀態參數估計的跟蹤精度。文獻[8]針對多軸分布式電驅動車輛，通過建立雙重無跡卡爾曼濾波器(DUKF)對車輛狀態和車輛參數進行聯合估計。文獻[9]基于三容積卡爾曼濾波理論設計了車輛狀態與參數聯合估計算法，通過三個估計器間信息的相互校正，進一步提高了算法的準確性。

針對普通算法的估計精度不高及實時性不好，容積卡爾曼濾波因系統模型不準確可能出現結果發散等問題。本文提出一種聯邦-容積卡爾曼濾波方法，聯邦卡爾曼濾波是從分散化濾波的基礎上逐漸發展而來的，具有設計靈活、容錯性好的特點，這種相結合的方式充分利用了各自的優點，可以使過程噪聲在估計過程中自適應變化，具有較高的估計精度和良好的容錯性以及穩定性。論文選取融合重置結構對兩個子濾波器和一個主濾波器進行設計，并對每一個子濾波器中的時間更新和測量更新采用容積卡爾曼濾波算法，最后通過實驗對該法進行了驗證。

2 車輛估計模型

2.1 分布式驅動電動汽車車輛動力學模型

車輛動力學模型表征著汽車在運動過程中不同參數變量之間的數學關系，是設計車輛狀態與參數估計算法的基礎。針對分布式驅動電動汽車，考慮到整個估計算法的時效性以及縱向、側向和橫擺三個方面的運動，依據傳統二自由度模型建模方法，并在此基礎上進行相應假設建立三自由度車輛估計模型。模型進行假設如下：

1)坐標原點與質心重合。

2)假設車輛由一個剛性車體和四個相互獨立控制的車輪構成。

3)假設各輪胎機械特性相同。

4)忽略懸架系統作用。

車輛模型如圖1所示。

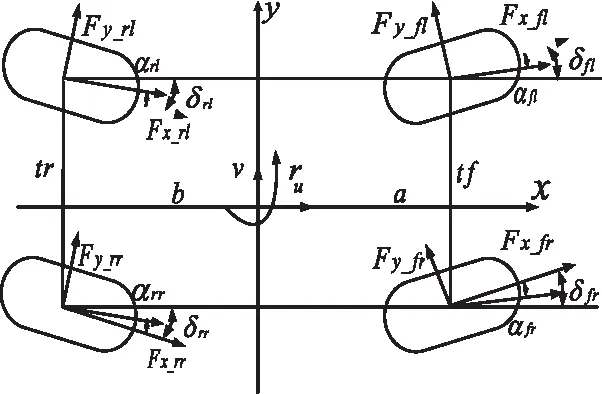
圖1 車輛動力學估計模型

圖1中：

a

和

b

分別為質心至前、后軸的距離，

t

和

t

分別為前、后輪輪距，

v

為車輪中心速度，

δ

為通過轉向電機直接獲取的四輪轉角，

F

＿為輪胎縱向力，

F

＿為輪胎側向力，

α

為輪胎側偏角。其中，

i

代表前輪或者后輪，

j

代表左輪或右輪。

車輛動力學模型方程如(1)、(2)、(3)所示

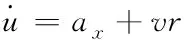
(1)

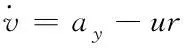
(2)

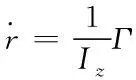
(3)

式中：

v

和

u

分別為縱

/

側向車速，

a

和

a

分別為縱

/

側向加速度，

r

為橫擺角速度，

I

為汽車繞

z

軸的轉動慣量，Г為橫擺力矩。由動力學模型計算

a

、

a

和Г公式如式(4)、(5)、(6)所示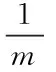

+

F

＿cos

δ

+

F

＿sin

δ

+

F

＿cos

δ

+

F

＿sin

δ

)

(4)

-

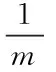
F

＿cos

δ

+

F

＿sin

δ

-

F

＿cos

δ

+

F

＿sin

δ

) (5)

(6)

式中，四輪的側偏角、線速度和法向反作用力計算公式如式(7)、(8)、(9)所示

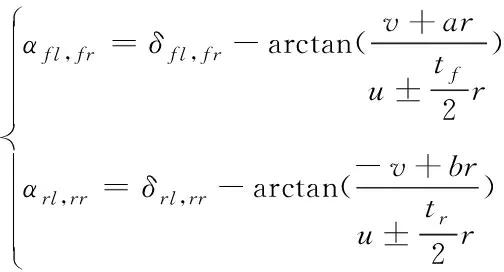
(7)

{

v

，=(

u

±

t

2

r

)+(

v

+

ar

)

v

，=(

u

±

t

2

r

)+(

v

-

br

)

(8)

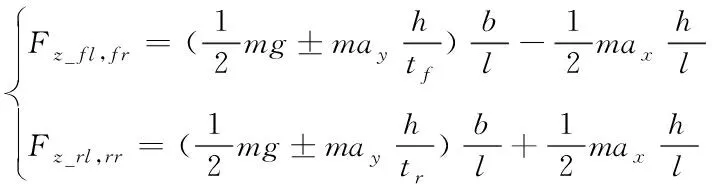
(9)

式中：

F

＿為地面對車輪的法向反力，

m

為整車質量，

l

為軸距，

h

為質心高度。

四輪縱向力可通過式(10)進行計算

(10)

2.2 側向力計算

采用Dugoff 輪胎模型計算四輪的側向力，公式如式(11)所示

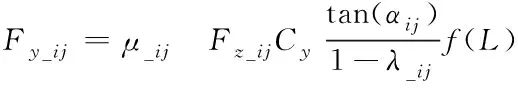
(11)

式中：

μ

＿為路面附著系數，

C

為輪胎側偏剛度，

λ

＿為縱向滑移率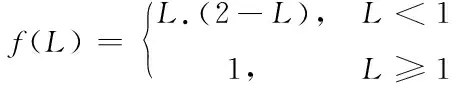

(12)

(13)

式中：

C

為輪胎縱向剛度，

ε

為速度影響因子。

制動和驅動對應的滑移率公式如式(14)所示

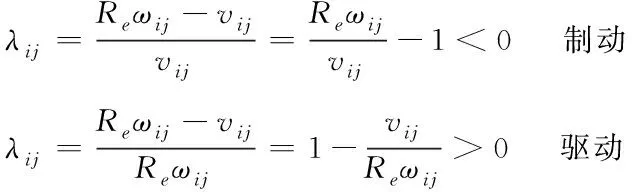
(14)

3 車輛狀態與參數聯合估計算法設計

3.1 聯合估計原理

分布式驅動電動汽車狀態與參數聯合估計原理示意圖如圖2所示。首先通過整車通訊網絡采集車載傳感器信號，主要包括車輛的縱向加速度、側向加速度、橫擺角速度、四輪轉角、四輪轉速和四輪驅動力矩。將這些傳感器信號同時傳輸給行駛狀態估計器、附著系數估計器和車輛參數估計器中各主

/

子濾波器以及Dugoff輪胎模型作為算法模型的信號輸入。經過輪胎模型解算出輪胎側向力，通過輪胎縱向力計算模塊將采集到的四輪驅動力矩直接換算成四輪所受的縱向力，以減小輪胎模型本身對計算輪胎力所產生的誤差。將所得到的輪胎力又作為各個估計器中各主/子濾波器的另一個輸入。與上一章的聯合估計算法所不同的是算法模型中的車輛自身參數不再設定為固定值，而是接收來自算法估計器實時估計得到的修正值。三個聯合估計器中的主濾波器在接收到這些信號后進行初始化，信息分配系數默認值為零，將車輛參數變量、行駛狀態變量、附著系數變量、協方差矩陣和過程噪聲矩陣相應分配給各子濾波器，每一個子濾波器對所接收到的傳感器信號和分配后的信號進行整合，首先完成時間更新得到先驗狀態估計值，再根據各自的測量值完成測量更新得到后驗局部估計值，再將這些數據一同傳遞給主濾波器進行整合完成全局最優估計。最優估計值作為輸出的同時又按照特定的分配原則再次對各子濾波器進行信息分配，從而完成一次迭代，隨著時間不斷迭代在三個估計器中各自形成閉環。同時全局最優車輛參數估計值又反饋給行駛狀態估計器、路面附著系數估計器與輪胎模型，全局最優行駛狀態估計值又反饋給路面附著系數估計器、車輛參數估計器與輪胎模型，全局最優路面附著系數估計值又反饋給行駛狀態估計器、車輛參數估計器與輪胎模型。車輛狀態與參數進行實時修正并及時反饋，不僅在每個估計器內部形成閉環系統，整個系統在三個估計器外也形成閉環，由此完成對車輛狀態與參數的準確估計。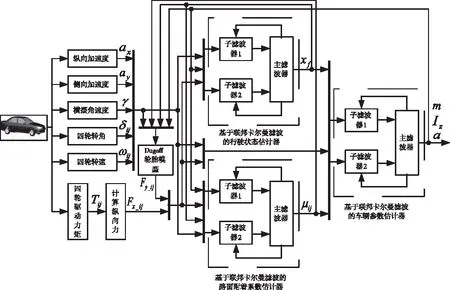

圖2 聯合估計原理圖

3.2 聯合估計算法

聯合估計算法具體設計過程如式(15)～(71)所示。

1)車輛自身參數的信息分配過程

首先通過主濾波器將車輛自身參數變量、誤差協方差矩陣與系統過程噪聲協方差矩陣，按照信息分配的原則分配給每一個子濾波器。

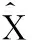
(15)

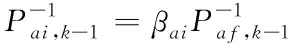
(16)

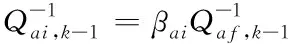
(17)

式中：

β

為車輛自身參數信息分配系數，其中

i

=1，2(即兩個子濾波器)，根據信息守恒有

β

+

β

2=1。

2)車輛行駛狀態的信息分配過程

首先通過主濾波器將行駛狀態變量、誤差協方差矩陣與系統過程噪聲協方差矩陣，按照信息分配的原則分配給每一個子濾波器。

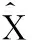
(18)

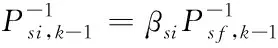
(19)

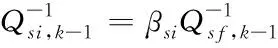
(20)

式中：

β

為行駛狀態信息分配系數，其中

i

=1，2(即兩個子濾波器)，根據信息守恒原則有

β

+

β

2=1。

3)路面附著系數的信息分配過程

通過主濾波器將路面附著系數參數變量、誤差協方差矩陣與系統過程噪聲協方差矩陣，按照信息分配的原則分配給每一個子濾波器。

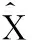
(21)

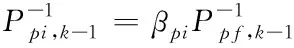
(22)

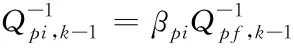
(23)

式中：

β

為路面附著系數信息分配系數，其中

i

=1，2(即兩個子濾波器)，并根據信息守恒原則有

β

+

β

2=1。

4)車輛自身參數的時間更新過程

在每一個車輛自身參數子濾波器中單獨進行時間更新。

①采用SVD法將協方差矩陣

P

，-1進行分解

(24)

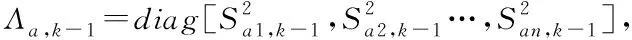
②計算前一時刻的容積點

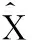
(25)

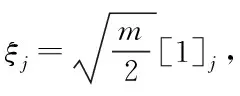
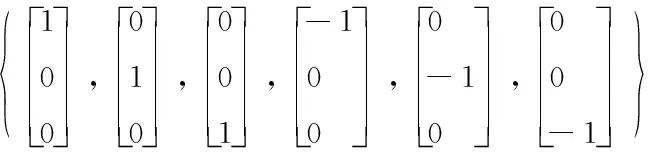
③計算系統方程迭代后的容積點

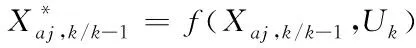
(26)

④估計經過時間更新后的狀態預測值

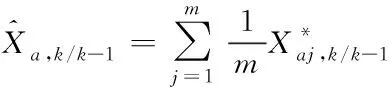
(27)

⑤估計誤差協方差矩陣的預測值

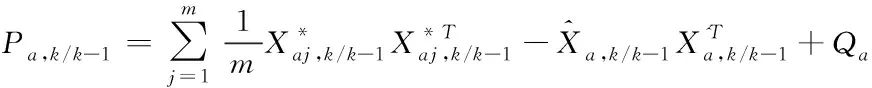
(28)

式中：

Q

為車輛參數過程噪聲協方差矩陣。

5)車輛行駛狀態的時間更新

在每一個行駛狀態子濾波器中獨立進行時間更新。

①采用SVD法對協方差矩陣

P

，-1進行分解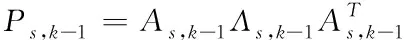

(29)

式中：

A

，-1為行駛狀態協方差矩陣

P

，-1所對應的特征矩陣。

②計算前一時刻的容積點：

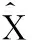
(30)

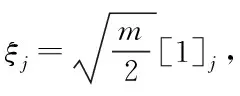
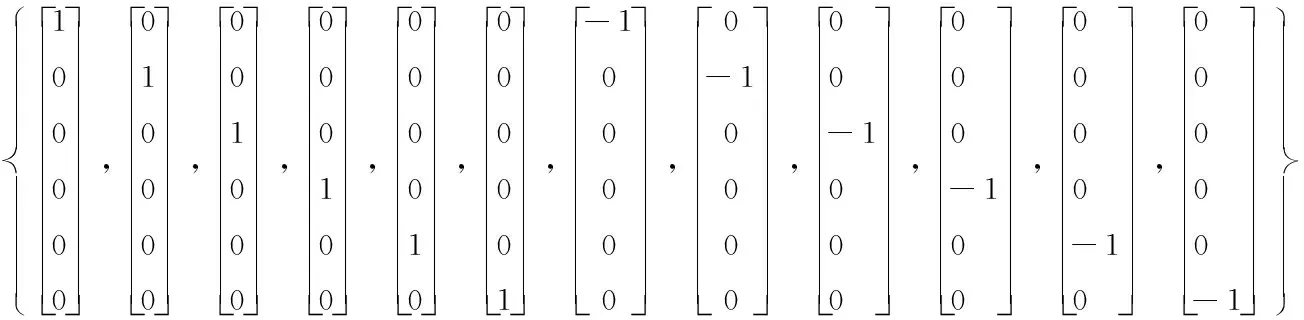
③計算系統方程迭代后的容積點

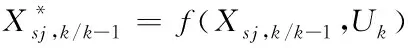
(31)

④估計經過時間更新后的狀態預測值

(32)

⑤估計誤差協方差矩陣的預測值

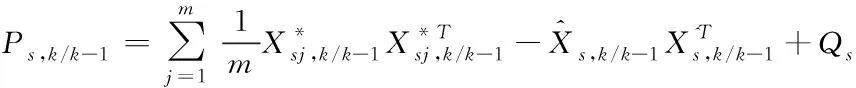
(33)

式中：

Q

為行駛狀態過程噪聲協方差矩陣。

6)路面附著系數的時間更新

在每一個路面附著系數子濾波器中獨立進行時間更新。

①采用

SVD

法對協方差矩陣

P

，-1進行分解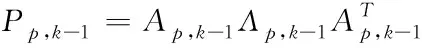

(34)

式中：

A

，-1為路面附著系數協方差矩陣

P

，-1所對應的特征矩陣。

②計算前一時刻的容積點：

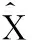
(35)

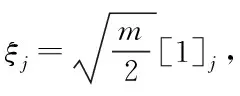
③計算經過轉移方程迭代后的容積點

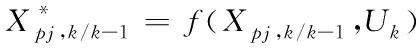
(36)

④估計經過時間更新后的預測值：

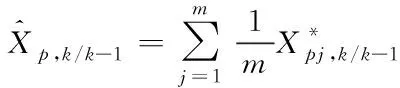
(37)

⑤估計誤差協方差矩陣的預測值

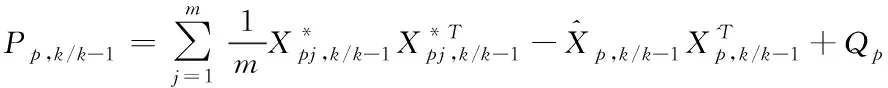
(38)

式中：

Q

為路面附著系數過程噪聲協方差矩陣。

7)車輛自身參數的測量更新過程

在每一個車輛自身參數子濾波器中單獨進行測量更新。

①采用

SVD

法將預測的協方差矩陣

P

，-1進行分解：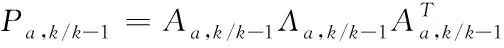

(39)

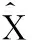
(40)

③根據測量變量計算新的容積點：

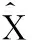
(41)

④對容積點求均值

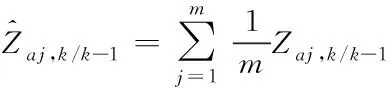
(42)

⑤計算新息方差

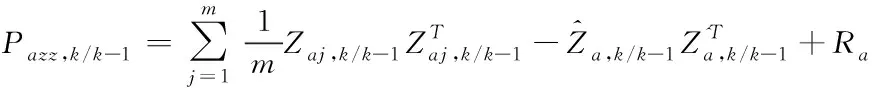
(43)

式中：

R

為車輛自身參數測量噪聲協方差矩陣。

⑥計算互協方差

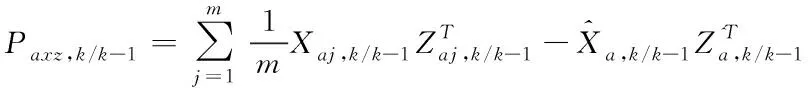
(44)

⑦計算濾波增益

(45)

⑧經過測量變量校正后的狀態估計：

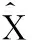
(46)

⑨校正誤差協方差矩陣：

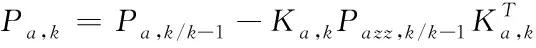
(47)

8)車輛行駛狀態的測量更新過程

在每一個行駛狀態子濾波器中單獨進行測量更新。

①采用SVD法將預測的協方差矩陣

P

，-1進行分解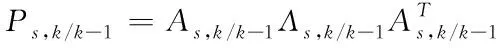

(48)

②計算容積點

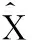
(49)

③根據測量變量計算新的容積點

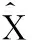
(50)

④對容積點求均值

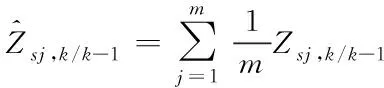
(51)

⑤計算新息方差

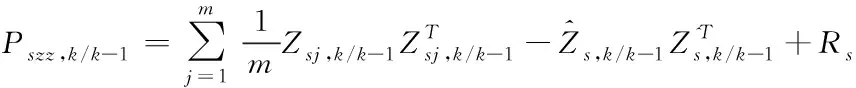
(52)

式中：

R

為行駛狀態測量噪聲協方差矩陣。

⑥計算互協方差

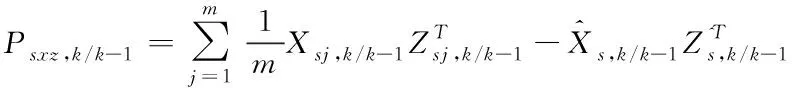
(53)

⑦計算濾波增益

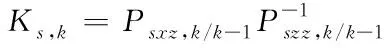
(54)

⑧經過測量變量校正后的狀態估計

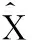
(55)

⑨校正誤差協方差矩陣：

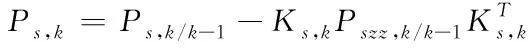
(56)

9)路面附著系數的測量更新過程

在每一個路面附著系數子濾波器中單獨進行測量更新。

①采用SVD法將預測的協方差矩陣

P

，-1進行分解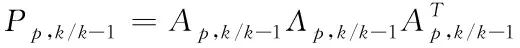

(57)

②計算容積點

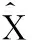
(58)

③根據測量變量計算新的容積點

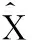
(59)

④對容積點求均值

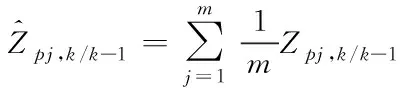
(60)

⑤計算新息方差

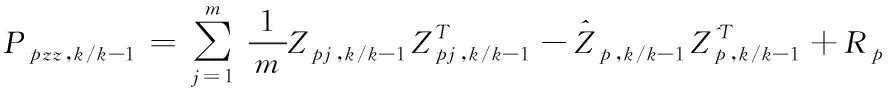
(61)

式中：

R

為路面附著系數測量噪聲協方差矩陣。

⑥計算互協方差

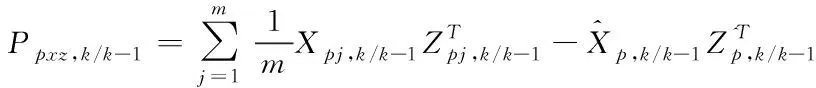
(62)

⑦計算濾波增益

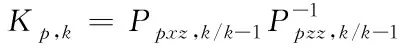
(63)

⑧經過測量變量校正后的狀態估計

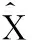
(64)

⑨校正誤差協方差矩陣

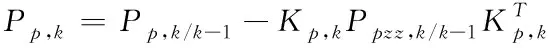
(65)

10)車輛自身參數的信息融合過程

對車輛自身參數中各子濾波器的局部估計值通過主濾波器進行融合得到全局最優估計。

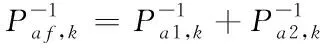
(66)

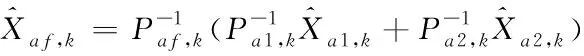
(67)

11)車輛行駛狀態的信息融合過程

對車輛行駛狀態中各子濾波器的局部估計值通過主濾波器進行融合得到全局

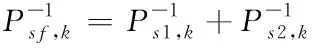
(68)

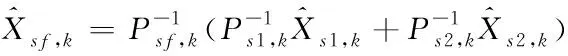
(69)

12)路面附著系數的信息融合過程

對路面附著系數中各子濾波器的局部估計值通過主濾波器進行融合得到全局最優估計

(70)

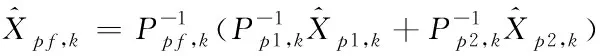
(71)

建立非線性系統的狀態與量測方程并給出各變量所含參數，公式如式(72)所示：

X

，=

f

(

X

，-1，

U

，-1，

W

，-1)

Z

，=

h

(

X

，，

v

，)

(72)

車輛自身參數估計器中兩個子濾波器的狀態變量為：

X

，=[

m

，

I

，

a

]。行駛狀態估計器和附著系數估計器中兩個子濾波器的狀態變量分別為：

X

，=[

u

，

v

，

a

，

a

，

γ

，

Γ

]，

X

=[

μ

，

μ

，

μ

，

μ

]。

行駛狀態估計器中子濾波器1，2的測量變量分別為：

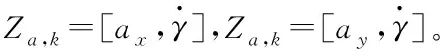
Z

，=[

a

，

a

，

γ

]，

Z

，=[

a

，

γ

]。

控制輸入量為：

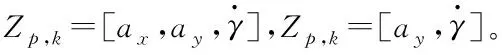
U

，=[

δ

，

δ

，

δ

，

δ

，

ω

，

ω

，

ω

，

ω

]。其中：

δ

為四輪轉角，是通過傳感器采集方向盤轉角信號按照一定規則計算所得到的。

信息分配系數的確定是聯邦濾波器設計中的關鍵問題，合理的選取主濾波器和子濾波器之間的信息分配系數可有效改善子濾波器的算法估計精度和故障檢測靈敏度，從而保證全局估計的最優性。鑒于協方差矩陣能夠極大程度上反映各子濾波器的估計精度，因此將其作為衡量的指標計算信息分配系數。本論文采用式(73)的方式進行分配。

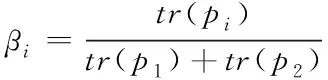
(73)

式中：

tr

(

p

)為誤差協方差矩陣的跡，并設定信息分配系數的初值

β

=

β

=0。

4 仿真驗證

為驗證所提出的估計算法的可行性和可靠性，在Matlab/Simulink環境下搭建相應的算法模型，同時與CarSim進行聯合仿真，評估估計算法對車輛非線性行駛狀態的估計效果。設置相應試驗工況，選擇低附著蛇形實驗工況。車輛模型部分參數如表1所示。

表1 車輛模型的部分參數

此工況的參數設置如下：車速為恒定值20km/h，附著系數設為0.2，采樣步長為0.02s。行駛狀態估計器中兩個子濾波器初值選取

X

1,0=[20

/

3

.

6,0,0,0,0,0]

P

1,0=

eye

(6)

Q

1,0=

eye

(6)

R

10=

diag

([0

.

0,1,15])*0

.

1

X

2,0=[20

/

3

.

6,0,0,0,0,0]

P

2,0=

eye

(6)

Q

2,0=

eye

(6)

R

20=

diag

([0

.

0,1])*0

.

01

路面附著系數估計器中兩個子濾波初值選取

X

1,0=[1,1,1,1]

P

1,0=

eye

(4)*2

Q

1,0=

eye

(4)

R

10=

eye

(3)*1000

X

2,0=[1,1,1,1]

P

2,0=

eye

(4)*2

Q

2,0=

eye

(4)

R

20=

eye

(2)*100

車輛參數估計器中兩個子濾波器初值選取

X

1,0=[700,1400,1]

P

1,0=

eye

(3)*100

Q

1,0=

eye

(3)*0

.

001

R

10=

eye

(2)*1000

X

2,0=[700,1400,1]

P

2,0=

eye

(3)*10

Q

2,0=

eye

(3)*0

.

1

R

20=

eye

(2)*10

仿真結果如圖3和圖4所示，其中圖3是CarSim仿真結果輸出的傳感器信號，即通過整車網絡采集的車載傳感器信號。圖4中的(a)、(b)、(c)、(d)、(e)、(f)和(g)為聯邦-容積卡爾曼濾波理論估計得到的車輛狀態與參數估計值與相應狀態參數實際值之間的對比結果。圖4(a)為縱向車速估計值與整車仿真模型輸出的實際值之間的對比曲線，從圖中曲線可以看出在仿真開始后，估計值與實際值保持良好的一致性，即使速度處于峰值時，兩者之間的誤差也非常小。圖4(b)為側向車速的估計值與實際值之間的對比曲線，圖4(c)為質心側偏角的估計值與實際值之間的對比曲線，估計值與實際值基本相吻合，在估計準確性、穩定性和實時性方面表現良好。圖4(d)為附著系數估計值與實驗工況所設定的實際值之間的對比曲線，在仿真初始時刻估計值就開始立即收斂到真實值處，待達到真實值附近開始處于穩定，在精度和穩定性方面表現良好。圖4(e)為質量的估計值與整車模型參數的設定值之間的對比曲線，圖4(f)為轉動慣量估計值與整車模型參數的設定值之間的對比曲線，圖4(g)為質心位置的估計值與整車模型參數的設定值之間的對比曲線，在仿真開始后估計值產生一些波動后都能迅速收斂到真實值處并保持穩定。綜上所述，估計算法在精度、實時性與穩定性方面都表現出良好的效果。

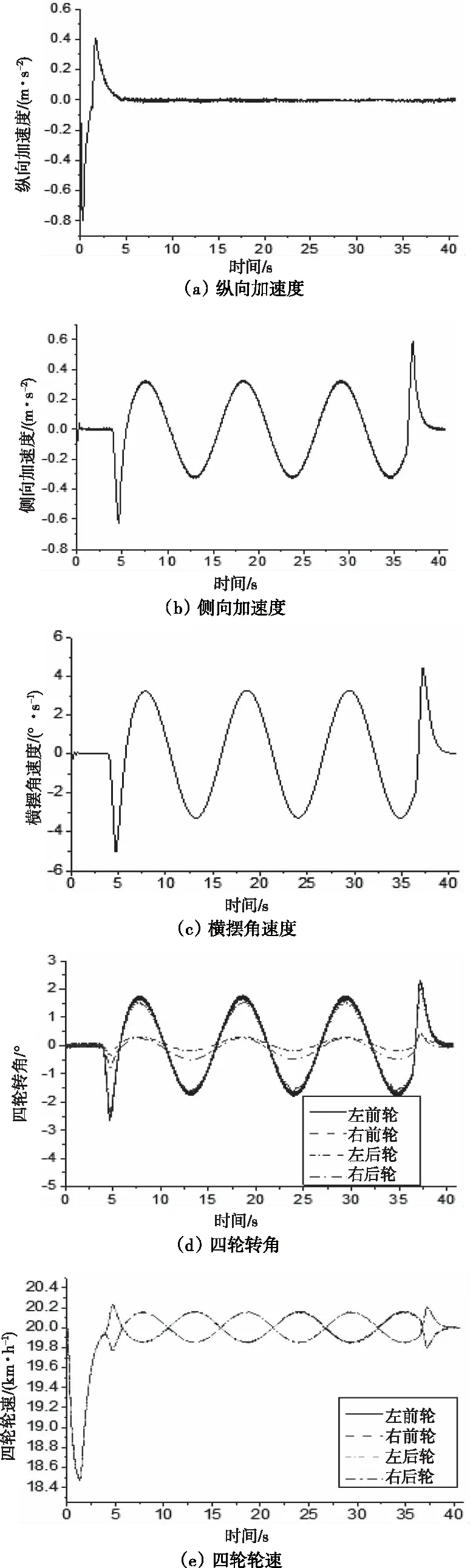
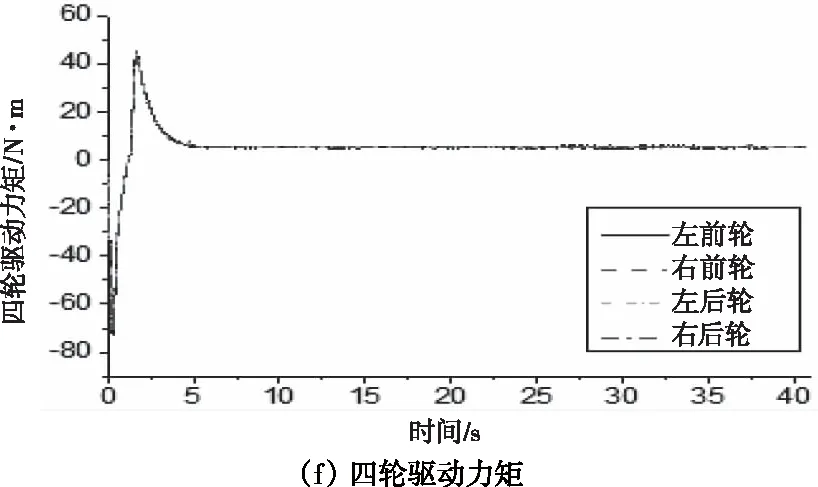
圖3 傳感器信號

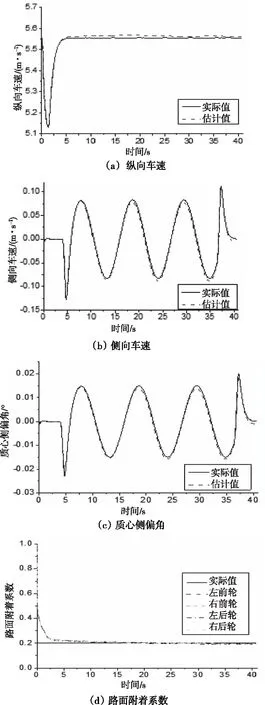
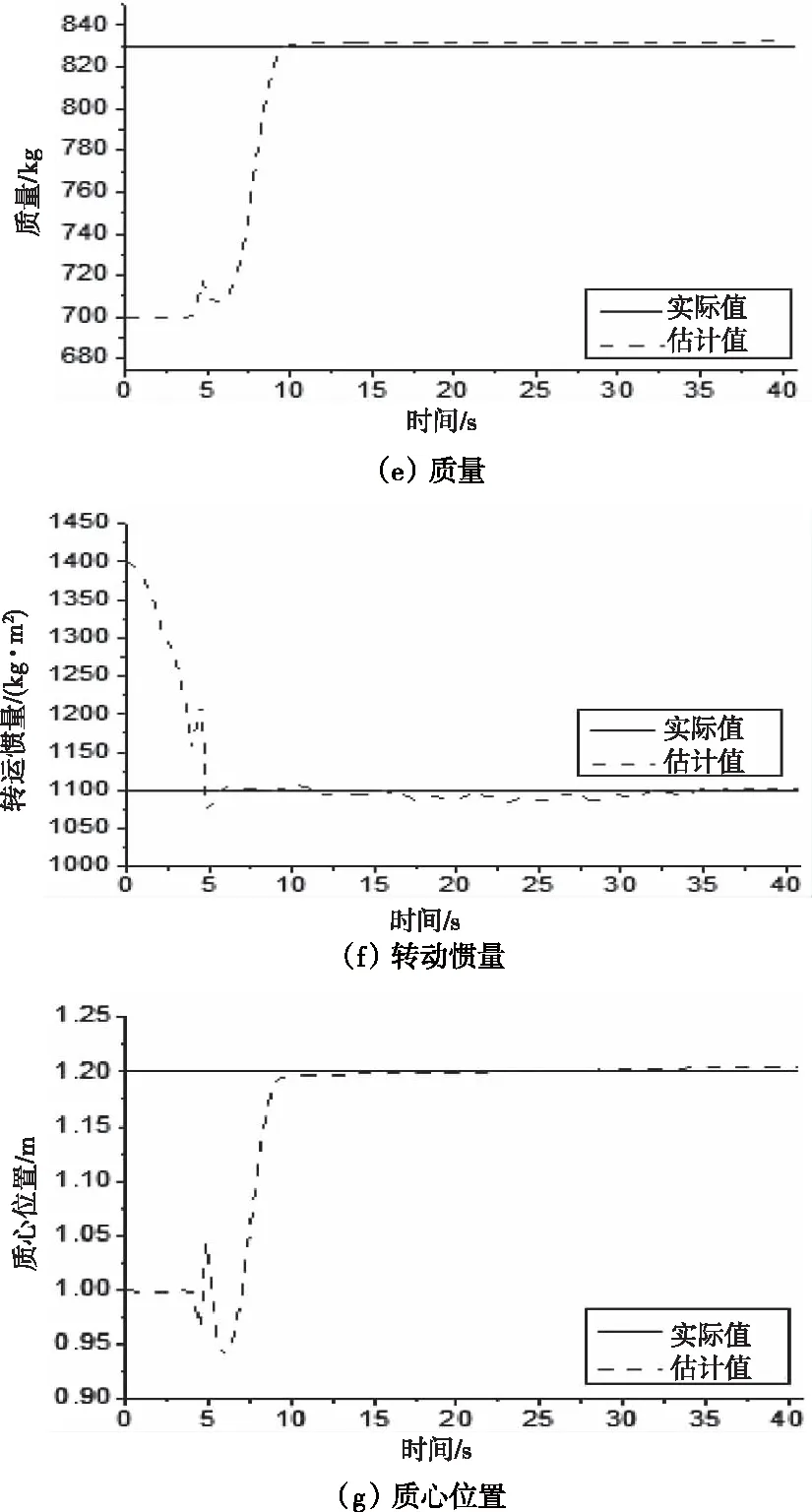
圖4 車輛行駛狀態與路面附著系數仿真輸出

5 結論

1)研究了一種聯邦-容積卡爾曼濾波方法對分布式驅動電動汽車的狀態與參數進行聯合估計，并采用兩個子濾波器和一個主濾波器的設計方式，其中子濾波器基于容積卡爾曼濾波理論進行設計，使過程噪聲在估計過程中自適應變化，提高了整個算法的估計精度。

2)運用Matlab/Simulink模塊化編程軟件對聯合估計算法模型進行搭建，并結合CarSim仿真平臺對算法進行實驗驗證，結果表明：該算法顯著提高了估計精度和穩定性、魯棒性好。