基于擾動觀察的雙饋風電場有功功率自動控制

陳麗敏，齊紅偉

(1. 青島科技大學自動化與電子工程學院，山東 青島 266000；2. 江蘇師范大學電氣工程及自動化學院，江蘇 徐州 221116)

1 引言

由于電力技術水平提升，風力發電機經過多次更新換代，雙饋型感應發電機具有運行穩定、體積小等優點被廣泛應用，該發電機的控制器對數學模型依賴性較強，且數學模型建立過程中的假設條件存在一定偏差，使風電場的有功功率與實際需求存在一定的偏差，為此需要對雙饋風電場有功功率進行有效控制。在眾多風電場有功功率控制方法中，何秀強等人設計的孤島啟動與并網控制方法利用空載運行方式實現有功功率控制，但受輸送端母線交流電壓和頻率變化的影響，使其控制耗時較長，因此控制效果不理想。榮飛等人設計的損耗最小化有功功率控制方法以降低風電機損耗方式實現有功功率控制，雖然較好地實現了風電場有功功率控制，但降低變流器設備功率方式僅適用于小型風電場。

擾動觀察方法以擾動方式對風電場輸出電壓進行干預，依據其輸出功率數值實現最佳功率跟蹤。為此本文設計基于擾動觀察的雙饋風電場有功功率自動控制方法，為風力發電行業發展提供相應技術支持。

2 基于擾動觀察的雙饋風電場有功功率自動控制

2.1 雙饋感應發電機運行原理

風力發電系統使用雙饋感應發電機通過風作用到其槳葉上使其轉動，且可在風力不同，槳葉轉速不同的情況下輸送電恒頻與電恒幅，其發電結構如圖1所示。

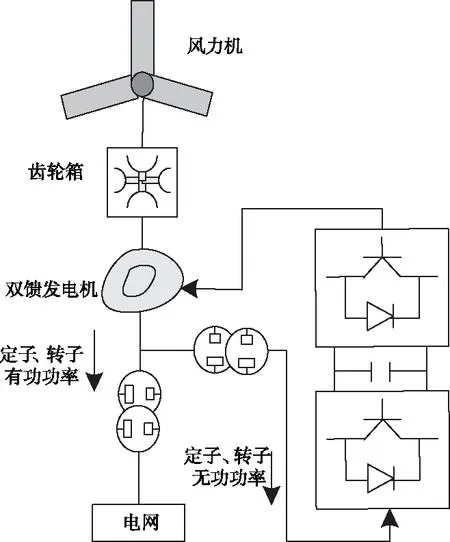
圖1 雙饋感應發電機發電結構示意圖

雙饋感應發電機可按照電網需求合理配置勵磁電流幅值、頻率等，其運轉模式為異步運行，假設該電機的轉子速度、受勵磁電流影響形成的與旋轉磁場相對的轉子轉速和同步轉子轉速分別為

c

、

c

、

c

，則三種轉速關系表達式如下

c

=

c

+

c

(1)

假設該電機的轉子頻率、勵磁頻率和電網頻率分別為

f

、

f

、

f

，則三種頻率關系表達式如下

f

=

f

+

f

(2)

通過式(2)可知，對發電機勵磁電流頻率的合理配置可使定子側的工頻電能保持穩定狀態。

2.2 雙饋感應發電機數學模型

在建立雙饋感應發電機數學模型時，利用

dq

坐標軸分量表示發電機相變量，令坐標軸內兩個軸方向的參數為一一對稱關系，依據發電機慣例，建立雙饋感應發電機電壓方程如下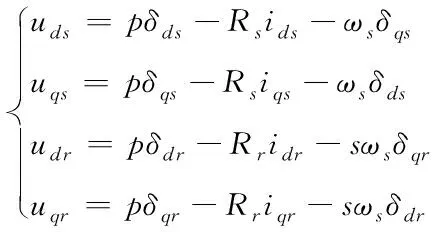

(3)

上述公式中，坐標軸內

d

軸的定子與轉子電壓分量為

u

、

u

，

q

軸的定子與轉子電壓分量為

u

、

u

，

d

軸的定子與轉子電流分量為

i

、

i

，

q

軸的定子與轉子電流分量為

i

、

i

，

d

軸的定子與轉子磁鏈為

δ

、

δ

，

q

軸的定子與轉子磁鏈為

δ

、

δ

，定子繞組電阻由

R

表示，轉子繞組電阻由

R

表示，

ω

則表示角速度，微分算子與滑差分別由

p

、

s

表示，

ω

為風頻。

雙饋感應發電機磁鏈數學模型為

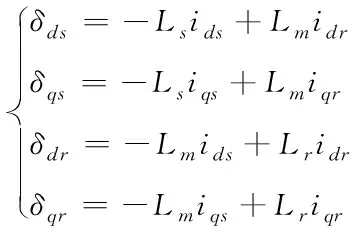
(4)

上述公式中，定子與轉子的繞組等效自感由

L

和

L

表示，定子與轉子之間的等效互感由

L

表示。

雙饋感應發電機轉矩數學模型為

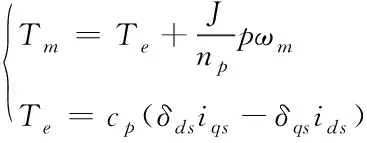
(5)

上述公式中，

ω

表示轉子機械旋轉角速度，電機對數由

c

表示。

雙饋感應發電機功率數學模型為

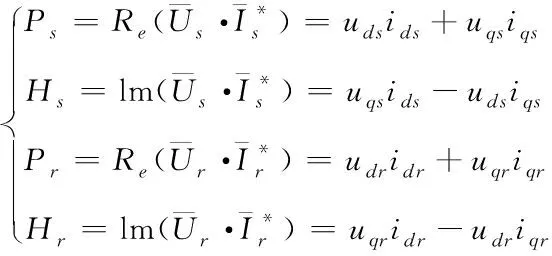
(6)

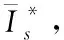
2.3 雙饋感應發電機動力學模型

在雙饋感應發電機發電結構內，風為風力機提供的機械功率表達公式如下

(7)

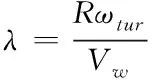
(8)

上述公式中，

ω

表示風力機機械角速度。

風能利用系數表達公式如下：

(9)

其中，

λ

的表達公式如下

(10)

分析風能利用系數公式函數特點得出，當扇尖速比為固定數值時，風能系數與槳距角呈反比例關系，當槳距角為固定數值時，扇尖速比和風能系數的最高數值互相對應，當風速條件相同時，可通過變更風力機旋轉速度時風能利用系數達到最高數值。

令

Z

(

ω

)表示風力機的等效阻抗，其計算公式如下

(11)

上述公式中，風力機等效電阻和等效電抗分別由

F

、

X

表示，風力機質量、附加質量和阻尼系數分別由

m

、

m

、

F

表示，

j

為可變常數。

通過式(11)可知，風力機的等效阻抗、等效電抗與電流和電壓性質相同。

當大氣運動較穩定的情況下，風速在某時間段內，風速變化情況不明顯，此時視為風力機具有穩定頻率，因此，風力機的附加質量與阻尼系數表達式如下

(12)

上述公式中，

ω

表示風力機穩定頻率。

將風力機處于穩定頻率時的附加質量和阻尼系數數值代入到式(11)內可知，穩定風速情況時風力機的等效阻尼和風頻率具有固定物理特性，此時風電場有功功率表達式如下

P

(

ω

)=

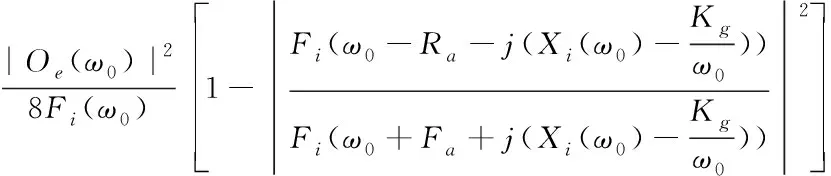
(13)

上述公式中，彈性系數由

K

表示，

O

表示風作用在扇葉上的力，利用上述步驟可獲取雙饋風電場動力參數。

2.4 基于擾動觀察風電場有功功率控制方法

依據雙饋風電場動力學模型和數學模型獲取風電場相關參數，其有功功率自動控制可利用變更風力機漿距和發電機勵磁電流的方式實現，在功率控制方面分為有功功率控制和無功功率控制，前者可通過獲取最高風能數值表達，即利用改變發電機轉速使風力機在切入風速與最高轉速過程中，其風能利用系數數值達到最高，而無功功率控制可利用恒功率因數與恒電壓實現控制，恒功率因數與恒電壓以變更無功功率參考數值，通過控制器勵磁電流與電壓使風電場輸出的無功功率發生變化，為使風能發揮其最大效應，在恒功率控制無功功率時，功率因數設置為常數1，當利用恒電壓方式控制無功功率時，以風電場與電網交接位置電壓作為控制電壓，因此無功功率變化數值為風電場與電網交接位置電壓上下浮動之差。

利用式(13)可知，當風頻率保持恒定的情況時，有功功率受阻尼系數和彈性系數影響表現為單峰值特點，此特性即為風力雙饋風電場有功功率輸出特性，其表現為在某特定風頻率下，利用阻尼系數與彈性系數構成的二維變量組使風電場輸出的有功功率數值最大。由于二維變量組的存在，無法利用單維度擾動觀察方式獲取最佳風電場輸出有功功率，因此，需要在兩個維度上增加阻尼系數與彈性系數交替擾動情況的第三維度，通過兩兩比較的方式獲取阻尼系數變化情況，從而獲取最大有功功率數值。本文利用分區域式變步長擾動觀察方法實現風電場有功功率控制，該方法通過斜率計算區域變更速度，經過對固定步長與斜率變步長添加擾動后，以尋找最佳數值方式降低功率點上下變化情況。當時間為

k

時，計算風電場的輸出功率數值，依據該功率數值曲線斜率角劃分為三個有功功率控制區域，區域的斜率角度數分別為0～30度、30～150度和150～180度，通過判斷角度分區，對有功功率以變步長的方式進行擾動并判斷擾動方向，依據擾動情況，更新風電場有功功率、阻尼系數以及彈性系數數值，從而實現風電場有功功率控制。分區域式變步長擾動觀察控制流程如圖2所示。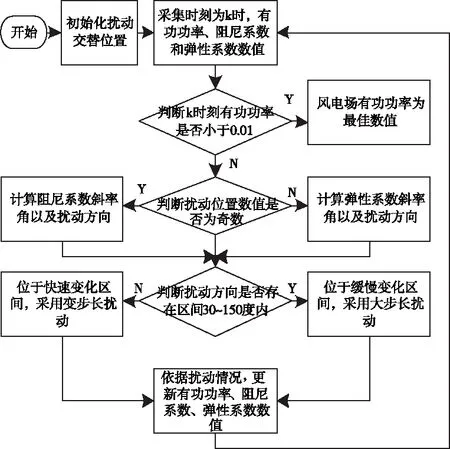

圖2 分區域式變步長擾動觀察控制方法

3 實驗分析

以某省大型雙饋風電場為實驗對象，該風電場配置為：裝機容量202MW，聯絡線電阻0.309Ω，功率約束限值41.3MW，風電場升壓站電壓等級110kV，為更加精準呈現本文方法控制效果，依據實際雙饋風電場運作數據，利用MATLAB仿真軟件模擬雙饋風電場運行，并利用本文方法、文獻[3]方法和文獻[4]方法對該風電場有功功率展開控制，其中，文獻[3]方法和文獻[4]方法分別表示孤島啟動與并網控制方法和損耗最小化的有功無功協調優化控制方法。

設置仿真時間為400s，風頻率分別為0～180s時保持時間為4s，風頻率為180～360s時，其時間周期呈現不斷變化趨勢，風頻率為360～520s時，風頻周期為6s，分別使用三種方法對該雙饋風電場有功功率進行控制，利用仿真軟裝輸出其風能捕獲曲線，結果如圖3所示。

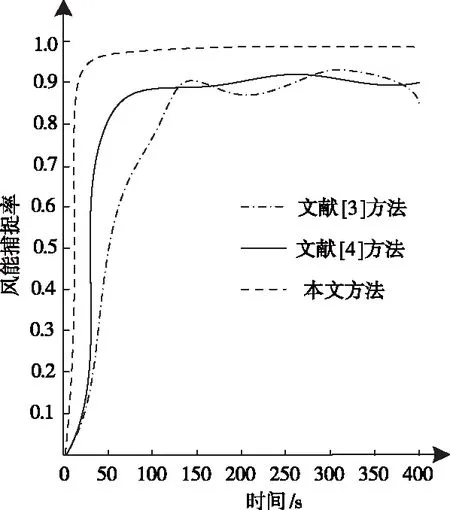
圖3 三種方法風能捕捉能力測試結果

分析圖3可知，三種方法的風能捕捉率均隨著時間的增加先呈現直線式上漲而后保持相對穩定狀態，其中，文獻[3]方法和文獻[4]方法的風能捕捉率分別在時間為140s和50s時達到相對穩定數值，但二者的風能捕捉率均出現不同程度的波動情況，表明兩種控制方法控制狀態不佳，而本文方法的風能捕捉率在時間為25s左右已開始保持穩定狀態，且風能捕捉率數值始終保持在0.98左右，當時間為400s左右，其風能捕捉率數值接近1.0，遠高于對比方法，由此可知，本文方法控制雙饋風電場的風能捕捉效果較好。

在仿真軟件內設置電壓急速下降工況，繪制三種方法控制下的直流電容電壓變化曲線，結果如圖4所示。

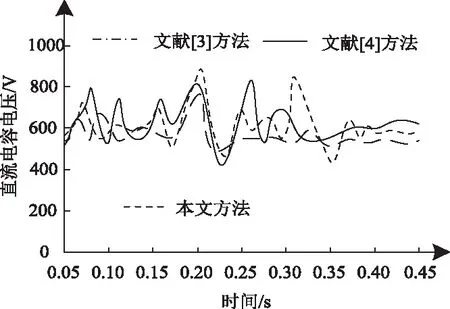
圖4 三種方法控制的雙饋風電場直流電容電壓曲線

分析圖4可知，文獻[3]方法和文獻[4]方法控制的風電場電容電壓曲線波動幅度較大，曲線振蕩時間較長，表明兩種方法控制的電容電壓不穩定，控制效果較差，而本文方法在時間為0.22s之前控制的電容電壓曲線雖存在一定波動幅度，但波動數值較低，當時間超過0.22s后，本文方法控制的電容電壓曲線較為平緩，波動起伏不大，表明本文方法控制的風電場有功功率回路與無功功率回路之間的解耦關系較好，有功功率的變化對風電場直流電容電壓影響較小。

繪制三種方法控制下的風電場無功功率曲線，對比三種方法控制無功功率補償有功功率效果，結果如圖5所示。

圖5 三種方法控制無功功率補償有功功率效果

分析圖5可知，文獻[3]方法和文獻[4]方法控制的無功功率曲線波動較為相似，由于電壓急速下降，下降后的風電場瞬態峰值相對較高，遠高于風電場撬棒保護觸發數值，從上圖三種方法無功功率波形上看，無功功率曲線經過短暫的波動后返回到穩定狀態，表明此時風電場有功功率得到有效控制，由此可見，本文方法可使風電場有功功率迅速恢復到其所需數值。

為更直觀體現其有功功率控制效果，在仿真軟件內設置額定有功功率數值，在不同風速情況下，測試三種方法有功功率控制情況，結果如表1所示。

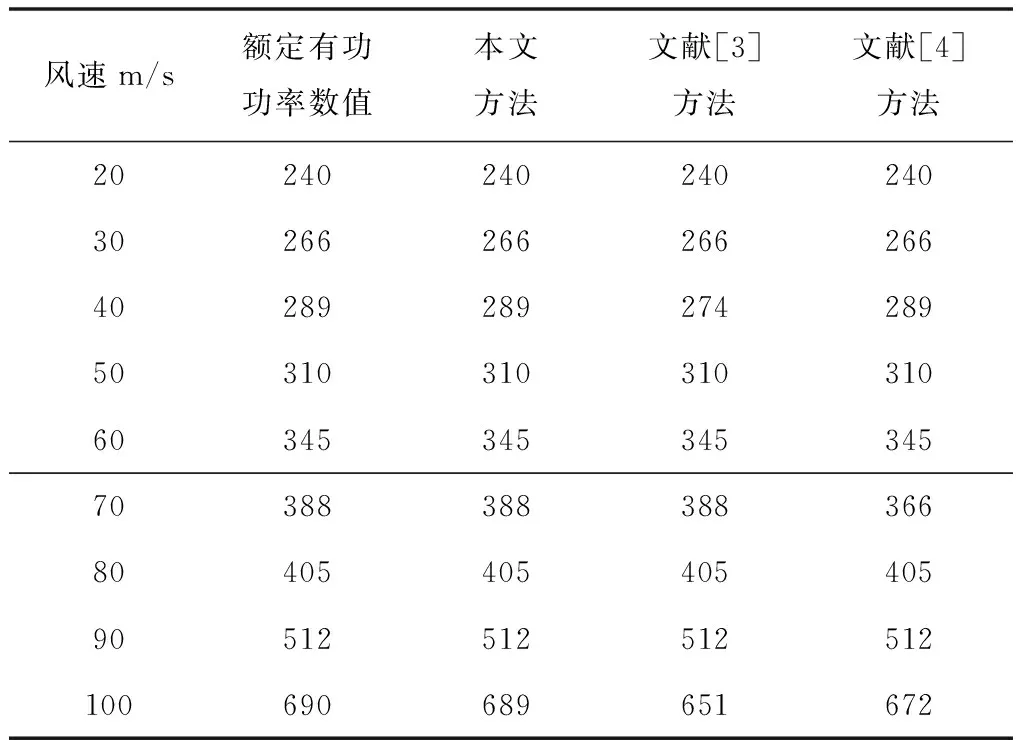
表1 三種方法有功功率控制情況/kW

分析表1可知，隨著風速的增加，三種方法控制的有功功率數值均出現不同程度偏差，其中，文獻[3]方法和文獻[4]方法控制的有功功率數值均出現兩次偏差，二者偏差最大數值分別為39kW和22kW，而本文方法控制的有功功率數值在風速為90m/s之前均和額定有功功率數值相同，僅在風速為100m/s時出現輕微偏差，偏差數值僅為1kW，由此可見，本文方法控制雙饋風電場有功功率效果較好。

4 結論

本文利用擾動觀察方法對基于擾動觀察的雙饋風電場有功功率自動控制展開研究，依據有功功率受阻尼系數和彈性系數影響表現為單峰值特點，設計分區域式變步長擾動觀察控制方法實現雙饋風電場有功功率控制。實驗結果表明：本文方法控制的雙饋風電場風能捕捉率始終保持在0.98左右，控制雙饋風電場的風能捕捉效果較好；控制電壓曲線波動幅度較小，控制的風電場有功功率回路與無功功率回路之間的解耦關系較好；在不同風速條件下，控制有功功率與額定有功功率僅出現一次偏差，且偏差數值僅為1kW，控制雙饋風電場有功功率效果較好。