對矢量網絡分析儀頻域至時域轉換過程的探究

申龍

（中國空空導彈研究院，河南洛陽，471009）

0 引言

矢量網絡分析儀是一種在微波領域內目前被廣泛使用的儀器,它通過掃頻原理得到測試結果，工作頻段寬且使用便捷，用戶可以根據需求通過改變顯示格式將散射參數轉換為不同的顯示形式如指數、駐波比和相位等表示出來，使測試結果簡潔直觀便于分析。同時，通過為矢量網絡分析儀加裝時域測試功能選件，能夠豐富其應用范圍，將原本的頻域分析拓展至時間域內[1]。本文主要對矢量網絡分析儀頻域至時域轉換過程進行探究，通過對離散傅立葉逆變換原理的探究推導出兩種算法并利用MATLAB軟件實現仿真及驗證。

1 傅立葉變換原理

法國數學家傅立葉首先提出了傅立葉分析理論，證明了將周期信號展開為正弦級數的原理，并以此為基礎發展出了傅立葉級數理論，而傅立葉變換則是基于傅立葉級數原理對非周期信號進行分析[2]。

通常來說，任何時域周期函數都可以描述為一系列諧波分量的疊加。通過使用函數f(t)和F(ω)作為在所有時間和所有頻率上的傅立葉變換對，可將連續傅立葉變換定義為如下公式：

而在矢量網絡分析儀中，測量值的幅度和相位都記錄在離散的頻率軸上，由于頻率軸的離散性及限于頻率范圍0≤f≤∞，因此不可能進行連續傅立葉變換與逆變換，因此需要使用離散傅立葉變換。假設有限長序列x(n)的長度為N（范圍為0≤n≤N?1），它的離散傅立葉變換X(k)也是一個長度為N的頻域序列（范圍為0≤n≤N?1），則離散傅立葉變換對為：

式中n代表離散的時間增量，k與頻率相似，單位為采樣點數/周期。需要注意的是，離散傅立葉變換在時域和頻域上都呈現離散的形式且變換兩端的序列都是離散周期信號的主值序列。矢量網絡分析儀頻域至時域的轉換基于離散傅立葉逆變換原理，同時在其基礎上進行了變化與修正。

2 矢量網絡分析儀頻域至時域轉換過程

需要首先說明的是，在矢量網絡分析儀頻域轉換至時域時使用的是經過修正的傅立葉逆變換。如圖1所示的一個三極點巴特沃斯濾波器的S11參數的解析變換，即反射頻率響應是通過標準網絡理論計算得到的并通過傅立葉逆變換計算出時間響應，與矢量網絡分析儀的時域變換功能所得到的時域響應對比，可以發現盡管在結構上有一定的相似性，但是二者明顯不同。矢量網絡分析儀的離散數據點采樣、頻域測量數據的加窗和截斷等原因導致了這種結果，所以在研究頻域至時域轉換過程時需要考慮這些因素[3]。

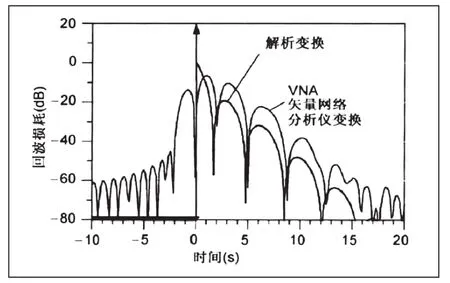
圖1 三極點巴特沃斯濾波器的解析沖激反射響應與矢量網絡分析儀時域變換響應

根據以上分析可知為了完成矢量網絡分析儀由頻域至時域轉換的過程的仿真，需要基于離散傅立葉變換提出新的修正算法。在這種情況下，快速傅立葉變換（FFT）與快速傅立葉逆變換（IFFT）算法被提出，它們利用離散傅立葉變換的對稱性和周期性將原來的N2復數乘法運算次數減少，合理地改善了離散傅立葉變換的運算時間。但是其在使用和表達數據上卻存在限制，快速傅立葉變換與其逆變換要求采樣數據和變換后數據具有相同點數并分布在變換后的時間范圍內。

由于矢量網絡分析儀時域分析的特殊性及靈活性，需要對任意時間步長的情況進行分析，因此引入線性調頻Z（Chirp-Z，CZT）變換算法。它基于FFT算法并且改善了時域轉換上的局限性，能夠在Z平面上完成特定時間區間螺旋線上的均勻采樣，具體算法定義如以下公式所示：

其中A0和θ0代表起始位置的半徑和相角，W0與Φ0確定了螺旋線的伸展率和相鄰相角間隔。其采樣原理如圖2所示。

圖2 線性調頻Z變換采樣原理圖

通過以上公式及采樣原理，可以得到Z平面上單位圓內任意頻段內等間隔的抽樣點[4]，實現特定時間區間CZT變換算法。同時，根據傅立葉變換的基本原理，即對共軛后的頻域數據做CZT變換后得到的數據再做共軛可以推導出線性調頻逆Z變換(ICZT)如公式（7）所示：

因此，通過使用ICZT算法，可以實現由已知的頻域響應數據得到任意時間段內的時域響應數據。

3 仿真與分析

根據前面的分析可知，矢量網絡分析儀頻域至時域轉換過程理論上可以使用IFFT和ICZT這兩種算法來進行仿真，本文基于矢量網絡分析儀的實際測試數據，搭配使用美國MathWorks公司的數學軟件MATLAB分別對兩種算法進行仿真運算及分析驗證。

3.1 IFFT算法

使用型號為N5245B的矢量網絡分析儀對一段電纜進行測試，頻率范圍為3GHz～6GHz,點數為201個，通過測試得到一組包含實部、虛部的S21參數的復數形式，利用MATLAB軟件使用傅立葉逆變換的方式將這組頻域數據進行變換到時域。

MATLAB軟件中內置有FFT和IFFT函數，可以對測試數據進行快速傅立葉變換及逆變換，但是在實際使用中，IFFT函數只對于經由FFT函數轉換后的數據具有較好的適配性，即對一組已知的時域數據使用FFT函數后得到的結果再使用IFFT函數能夠重新得到正確的時域數據，而對于已知的一組頻域數據而言，直接使用IFFT函數所得到的結果與實際結果誤差較大。

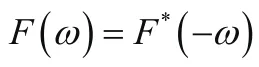
圖3 構造后的共軛對稱實部及虛部值

由圖4可見，IFFT轉換后所得到的時域數據其實部值在一時間點處有明顯的沖擊響應，根據傳輸線長度計算公式

圖4 IFFT轉換后的時域響應幅度值

其中l為傳輸線長度，k為傳輸線的相對傳輸速度，c為光速，t為傳輸線中的傳輸時間。

可以推測出被測電纜的實際長度，從而驗證此算法的正確性。在時域響應信號附近的震蕩是由于逆變換之前的頻域數據的截斷誤差所造成的振鈴效應。

但是，通過時域響應dB值計算公式

可以得到圖5顯示的圖像，其所包含的大部分數據屬于無用信息，并且分辨率極低，與矢量網絡分析儀的測試結果差別極大，無法應用于之后的數據分析工作。

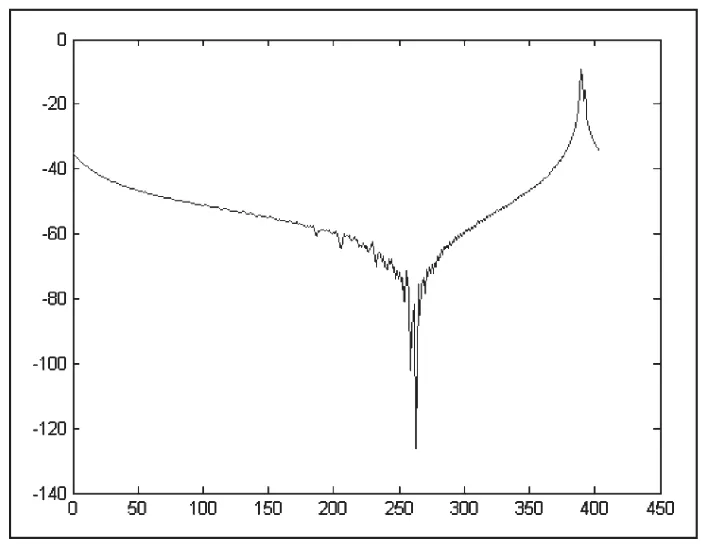
圖5 IFFT轉換后的時域響應值（dB）

3.2 ICZT算法

使用型號為N5245B的矢量網絡分析儀對一段電纜進行測試，頻率范圍為3GHz～6GHz,點數為201，通過測試得到一組包含實部、虛部的S21參數的復數形式，利用MATLAB軟件使用ICZT的方式將這組頻域數據進行變換到時域。事先通過觀察矢量網絡分析儀時域的實際測試數據可知，時域的沖激響應發生在1ns～3.95ns之間，因此，再做ICZT時，選擇起始時間為1ns～3.95ns。

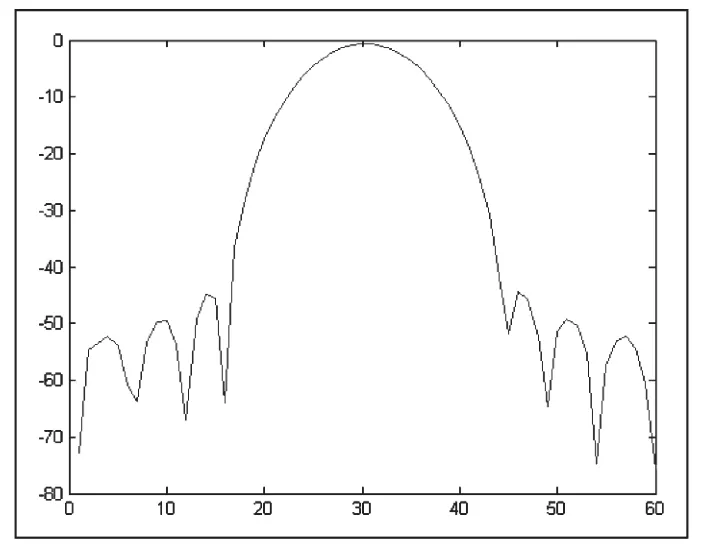
圖6 網絡分析儀測得的時域響應

由圖7可以看出，原始的頻域數據點數為201個點，而通過ICZT轉換后的圖像仍然保持了201個點數不變（ICZT甚至允許輸入輸出點數不同）。在實際時域數據結果中1ns～3.95ns區間包含60個點，對整個數據做一個interp1插值運算，將其擴充至201個點，之后與ICZT的結果做對比，如圖8所示，時域響應信號主瓣基本吻合，旁瓣峰值也吻合。以上仿真結果可以證明ICZT算法得到的時域數據與矢量網絡分析儀得到的實測數據的對比結果滿足誤差要求，可以用于之后的數據分析工作。

圖7 使用ICZT算法仿真得到的時域響應

圖8 仿真結果與實際結果對比

綜上所述，對采集的頻域響應信號直接使用IFFT算法后，所得到的時域響應包含的信息太過冗雜，且由于數據點數被平均分配至時域區間內圖像分辨率很低，導致仿真結果利用價值低，無法進行后續數據分析。而使用ICZT算法的方式能夠得到清晰、準確的時域圖像，完整實現了矢量網絡分析儀頻域至時域轉換過程，可以作為研究及分析時所使用的主要算法。

4 總結

本文通過探究矢量網絡分析儀的頻域至時域轉換過程，從傅立葉變換原理出發，介紹了IFFT與ICZT兩種頻域至時域轉換算法，通過應用MATLAB軟件進行仿真，實現了兩種算法的驗證及對比分析，為矢量網絡分析儀頻域至時域轉換的研究提供了理論依據及仿真數據參考。