密度非均勻分布緯編針織物的變形預(yù)測及仿真

汝 欣，朱婉珍，史偉民，彭來湖,3

(1.浙江理工大學(xué) 機(jī)械與自動控制學(xué)院，浙江 杭州 310018；2.浙江理工大學(xué) 浙江省現(xiàn)代紡織裝備技術(shù)重點實驗室，浙江 杭州 310018；3.浙江理工大學(xué)龍港研究院有限公司，浙江 溫州 325802)

為滿足針織物的設(shè)計樣式和功能的多樣化需求，一件緯編針織物成品往往是由不同密度(橫密、縱密)的緯編組織結(jié)合而成。如針織護(hù)膝、針織防曬袖等貼身衣物，需將其設(shè)計成密度非均勻變化的樣式來適應(yīng)人肢體粗細(xì)不均的特點。當(dāng)織物的密度分布不均勻時，織物成品的線圈并非是保持理想形態(tài)，而是會發(fā)生一定程度的變形。近幾年關(guān)于緯編針織物變形仿真問題，國內(nèi)學(xué)者主要研究的是線圈級別的變形：沙莎等[1-2]研究了在緯編基本組織中分別引入單個浮線、集圈和移圈線圈單元時線圈發(fā)生的變形；雷惠等[3]通過在織物中分別引入不同類型的線圈來研究它們對與其在同一橫列的線圈高度的影響，沒有考慮對縱行線圈尺寸的影響；國外一些學(xué)者關(guān)注到了織物的整體變形，Vajiha等[4]針對單雙面緯平針織物，提出了一種基于彈簧-質(zhì)點模型的模擬針織物卷邊的方法，仿真效果逼真；Karmon等[5]提出了針對織物整體變形及補(bǔ)償?shù)目椢锓抡嫦到y(tǒng)的構(gòu)想，但是沒有給出具體的實現(xiàn)方式。現(xiàn)有緯編針織物CAD變形仿真技術(shù)缺少針對密度非均勻分布的緯編針織物的變形研究。

本文以密度非均勻分布的緯編針織物為研究對象，提出一種確定密度非均勻分布的織物彈簧-質(zhì)點模型初始態(tài)的方法，基于二維Peirce線圈模型并結(jié)合織物圈距、圈高選取控制頂點建立NURBS線圈模型和質(zhì)點-控制點關(guān)聯(lián)式，最終實現(xiàn)變形織物的二維仿真模擬，為密度非均勻分布的緯編針織物的變形研究提供解決思路。

1 織物變形預(yù)測總體方案

本文基于緯編針織物密度非均勻分布的設(shè)計圖，對密度非均勻分布的緯編針織物變形預(yù)測及仿真方法進(jìn)行研究。圖1示出2種密度的織物組織結(jié)合時織物變形研究的圖形變化過程。

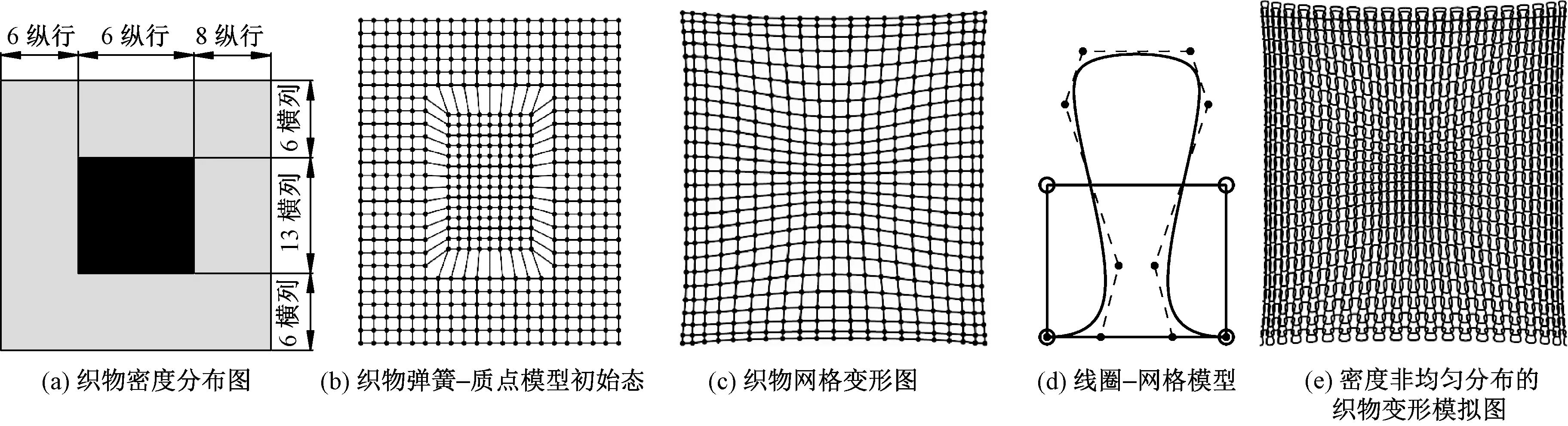
圖1 織物變形模擬過程Fig.1 Simulation process of fabric deformation.(a) Fabric density distribution ；(b) Initial state of spring-mass model of fabric;(c) Mesh deformation diagram of fabric;(d) Loop-mesh model ;(e) Deformation simulation of fabric with non-uniform density distribution;(f) Physical picture of a fabric with non-uniform density distribution

圖2示出主要研究流程，具體步驟如下：1)將織物的織物密度分布圖轉(zhuǎn)換成相應(yīng)的織物密度矩陣。密度非均勻分布的緯編針織織物的設(shè)計圖(后文簡稱為織物密度分布圖)是在織物結(jié)構(gòu)意匠圖的基礎(chǔ)上結(jié)合織物密度改進(jìn)而來,在織物密度分布圖中僅以顏色來區(qū)分不同密度的組織，其中，每種密度的組織均由相同結(jié)構(gòu)和大小的線圈組合而成。為便于說明，本文示例中的線圈結(jié)構(gòu)均為成圈。圖1(a)示出織物密度分布圖，表示的是由 2種密度的織物組織拼接而成的織物，其中黑色部分代表密度大的織物組織，淺灰色部分代表密度稍小的織物組織。

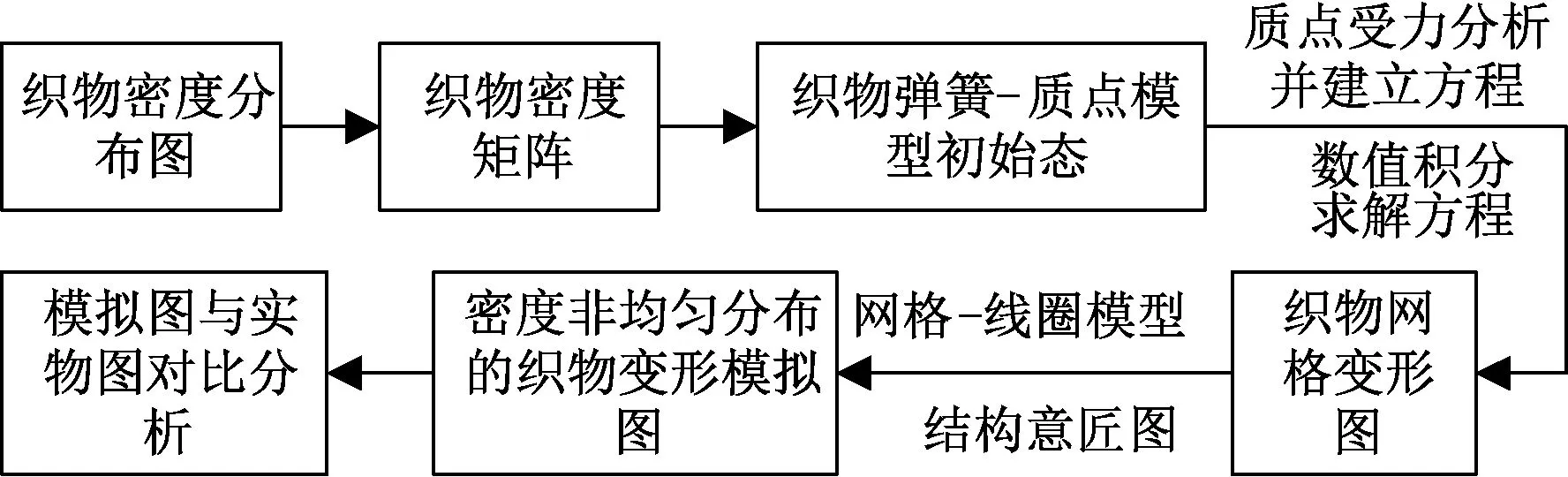
圖2 主要研究流程Fig.2 Main research process

2)從織物密度矩陣解析織物尺寸、位置等信息，確定織物彈簧-質(zhì)點模型初始態(tài)。如圖1(b)所示為與圖1(a)所示的織物密度分布圖對應(yīng)的織物彈簧-質(zhì)點模型初始態(tài)。

3)在織物彈簧-質(zhì)點模型初始態(tài)的基礎(chǔ)上結(jié)合力學(xué)分析計算出質(zhì)點受力偏移后新的位置，生成網(wǎng)格變形圖。圖1(c)為據(jù)圖1(b)生成的織物網(wǎng)格變形圖。

4)在織物網(wǎng)格變形圖基礎(chǔ)上建立曲線線圈模型，形成帶有曲線線圈的織物變形模擬圖。建立圖1(d) 所示網(wǎng)格-線圈模型，再根據(jù)織物結(jié)構(gòu)意匠圖來確定每個網(wǎng)格單元代表的線圈結(jié)構(gòu)，實現(xiàn)如圖1(e) 所示的帶有曲線線圈的織物變形模擬。

5)將圖1(e)所示織物變形模擬圖與實際樣品圖進(jìn)行比對，分析仿真效果的可靠性。

2 織物網(wǎng)格變形研究

由織物密度分布圖確定織物初始狀態(tài)的彈簧-質(zhì)點模型；在此基礎(chǔ)上運(yùn)用胡克定律和牛頓第二定律建立微分方程，采用Verlet數(shù)值積分法求解方程得到質(zhì)點在力的作用下新的位置，形成網(wǎng)格變形圖。

2.1 織物彈簧-質(zhì)點模型的建立與求解

建立織物的彈簧-質(zhì)點模型，即將織物離散成一群排列有序的質(zhì)點，質(zhì)點之間由彈簧(質(zhì)量忽略不計)連接。在織物的彈簧-質(zhì)點模型中，連接水平和豎直方向的質(zhì)點的彈簧為結(jié)構(gòu)彈簧；連接矩形單元格對角線方向質(zhì)點的彈簧為剪切彈簧；第3種彈簧為彎曲彈簧[6]，其彈簧系數(shù)較小，本文不考慮彎曲彈簧。通過控制質(zhì)點的坐標(biāo)位置來控制線圈的形態(tài)，最終實現(xiàn)整個織物的變形模擬。

為便于選取質(zhì)點，本文先將織物進(jìn)行簡化，平面的緯編針織物表面線圈呈縱、橫向排列分布，據(jù)此將織物以線圈為單位按照縱、橫2個方向進(jìn)行網(wǎng)格劃分，將織物簡化成二維網(wǎng)格[7]，線圈單元簡化成了四邊形單元格，如圖3(b)所示。在織物的二維網(wǎng)格圖中，二維網(wǎng)格縱、橫方向的單元格個數(shù)對應(yīng)織物縱、橫方向的針數(shù)，矩形單元格的高B、寬A對應(yīng)著理想線圈的圈高、圈距。

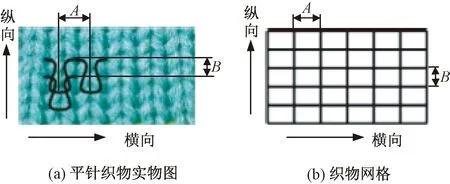
圖3 織物的二維網(wǎng)格Fig.3 Two-dimensional mesh of fabric.(a) Physical picture of weft plain fabric;(b) Fabric mesh

選取織物二維網(wǎng)格圖中單元格頂點作為質(zhì)點，單元格的寬、高為結(jié)構(gòu)彈簧的2種長度，單元格對角線長度為剪切彈簧的長度；橫列數(shù)m、縱行數(shù)n的針織物對應(yīng)(m+1)×(n+1)個質(zhì)點構(gòu)成的彈簧-質(zhì)點模型。圖4示出彈簧-質(zhì)點模型的示意圖。

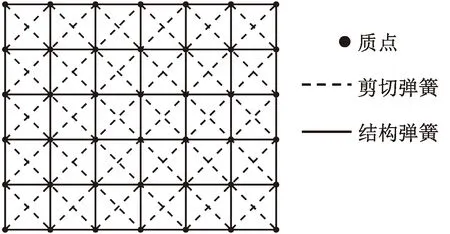
圖4 彈簧-質(zhì)點模型Fig.4 Spring-mass model

2.1.1 織物彈簧-質(zhì)點模型初始態(tài)的確定

為方便計算機(jī)讀取，需將織物密度分布圖進(jìn)行數(shù)字化處理：將織物的線圈以矩陣元素的形式存儲在矩陣中，矩陣中1個矩陣元素表示織物中對應(yīng)位置上的1個線圈，定義該矩陣為織物密度矩陣ρ。

(1)

式中：i=1,2,…,m;j=1,2,…,n；ρi，j=k表示織物中第i行第j列的類型為k的線圈，k=1,2,…;類型相同的線圈其所在織物組織的密度相同，將其所在組織也稱為組織k。矩陣行數(shù)m、列數(shù)n分別表示織物線圈的橫列數(shù)和縱行數(shù)。

在織物的網(wǎng)格圖中，不同密度的織物組織表現(xiàn)為不同大小的矩形單元格。根據(jù)織物密度矩陣ρ，確定織物第i行第j列的線圈k值，根據(jù)線圈的k值來確定該線圈所處組織的圈距和圈高，進(jìn)一步確定質(zhì)點的坐標(biāo)。說明密度均勻時根據(jù)線圈的類型值k,可確定質(zhì)點坐標(biāo)的方法。織物第i行第j列的線圈類型為k,其對應(yīng)的圈高和圈距分別為B、A,則該線圈的4個質(zhì)點坐標(biāo)值如圖5所示。

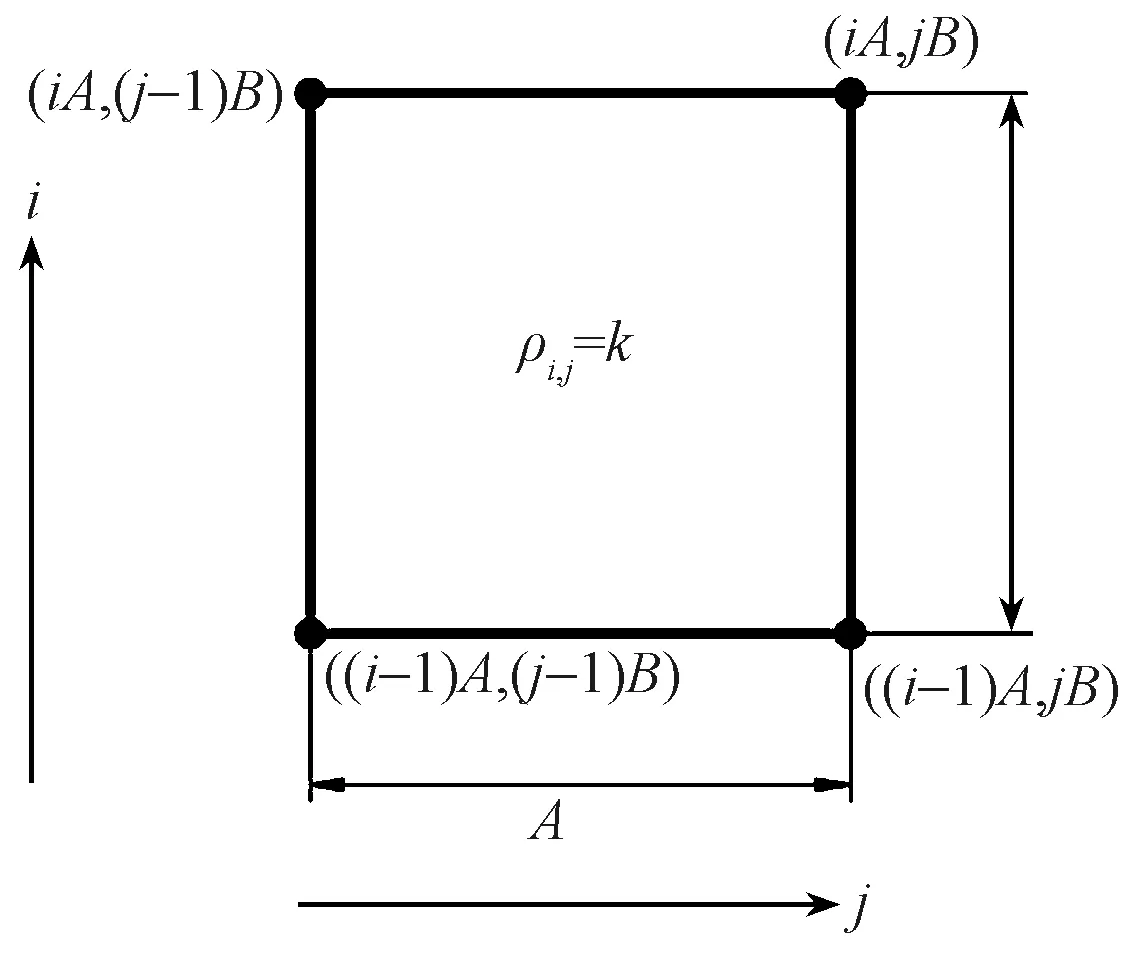
圖5 單個線圈坐標(biāo)與尺寸圖Fig.5 Coordinate and dimensional diagram of individual loop

現(xiàn)以圖1(a)所示的織物密度分布圖為例，說明其對應(yīng)的密度非均勻分布織物的初始狀態(tài)的彈簧-質(zhì)點模型建立過程。

圖1對應(yīng)的織物密度矩陣ρ為

(2)

其中,

圖1(a)所示織物是由2種密度的組織拼接而成，這2種密度分別為組織1、組織2(中間密集部分)。先假定所有組織的矩形單元格的寬度和高度都為組織1的寬、高來賦予質(zhì)點坐標(biāo)值初值，形成如圖6(a)所示網(wǎng)格；接著根據(jù)織物密度矩陣確定織物中組織2的線圈在織物中的位置，將組織2的實際大小所占據(jù)的區(qū)域(圖6(b)小方格組成部分)和組織2被當(dāng)成組織1所占據(jù)的區(qū)域(圖6(b)虛線方框框選)按照幾何中心重合的方式重新確定組織2各質(zhì)點的坐標(biāo)位置，形成圖6(b)所示的織物初始狀態(tài)的彈簧-質(zhì)點模型。

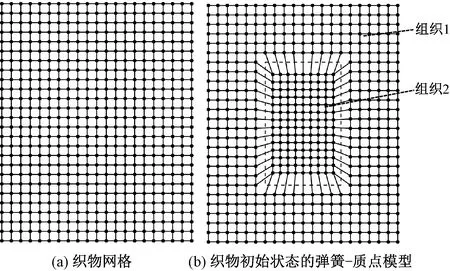
圖6 織物的彈簧-質(zhì)點模型Fig.6 Spring-mass model of fabric.(a) Fabric mesh;(b) Initial state of spring-mass model of fabric

從圖6(b)可以看到處于組織過渡處的線圈已經(jīng)不再是規(guī)則的四邊形，該四邊形的4個頂點處的質(zhì)點處于非平衡受力狀態(tài)，模擬了由于密度不同導(dǎo)致的2種密度過渡處織物受力不均衡的狀態(tài)。

2.1.2 質(zhì)點受力分析及微分方程的建立與求解

質(zhì)點的位移遵循牛頓第二定律：

F=amm

(3)

式中：F為質(zhì)點受到的內(nèi)力與外力的矢量和，本文不考慮外力的影響，因此這里的F即為彈簧的彈力(結(jié)構(gòu)彈簧力和剪切彈簧力);mm為質(zhì)點質(zhì)量；a為質(zhì)點加速度。由于采用的是理想彈簧，不考慮阻尼力，彈簧力F遵循胡克定律：

F=-KΔx

(4)

式中：K為質(zhì)點間彈簧的彈簧系數(shù)；Δx為彈簧的變形量。圖7為質(zhì)點受力分析圖。

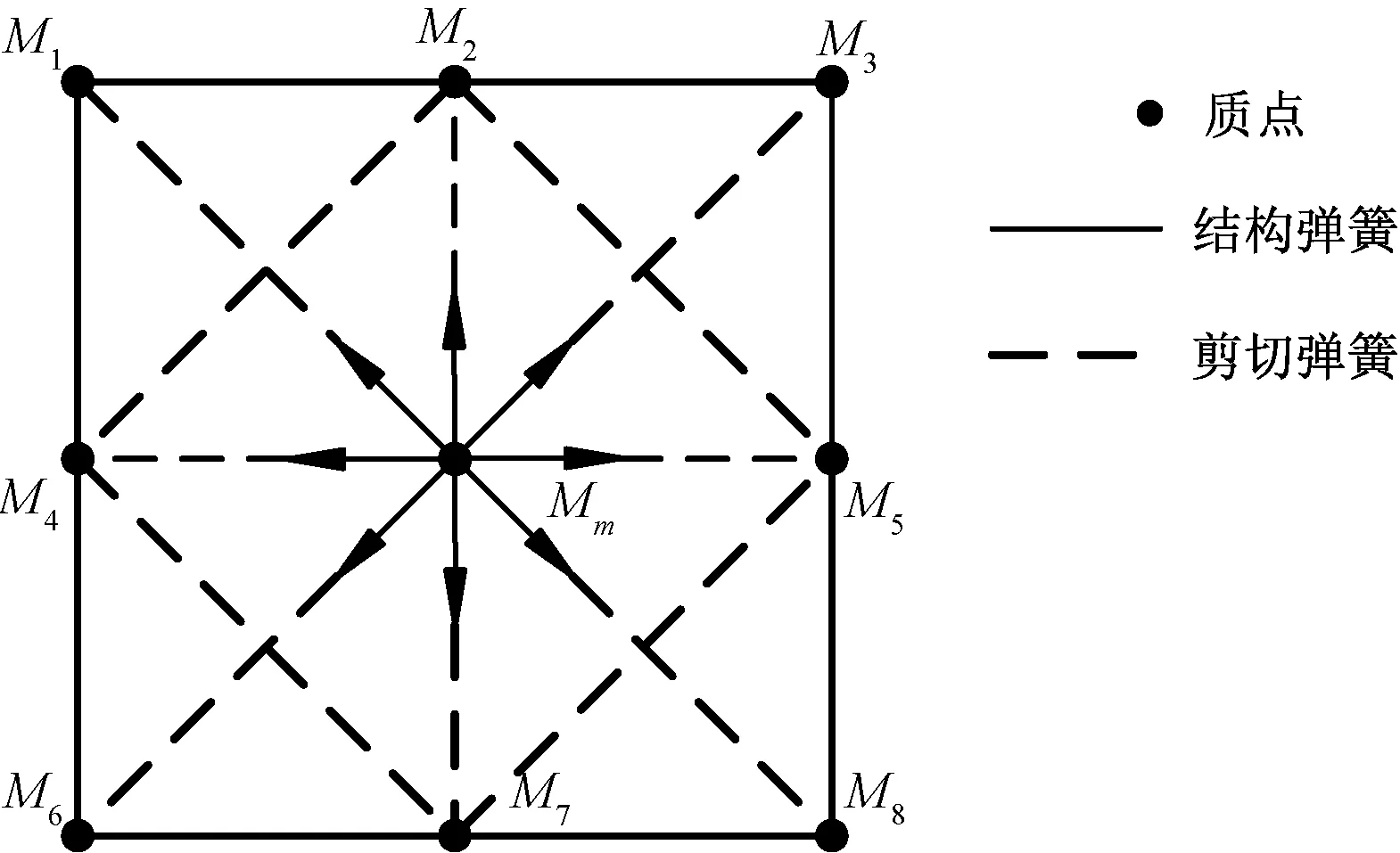
圖7 質(zhì)點受力分析圖Fig.7 Force analysis diagram of mass

假設(shè)當(dāng)前質(zhì)點為Mm,Mn是與Mm連接在一根彈簧上的質(zhì)點，則當(dāng)前質(zhì)點所受的彈簧力合力為

(5)

式中：n=1,2,…，8；Km,n為連接當(dāng)前質(zhì)點Mm與Mn之間彈簧的彈簧勁度系數(shù)；xm和xn分別為當(dāng)前質(zhì)點Mm和質(zhì)點Mn在t時刻的位置矢量；lm,n為彈簧原長。

Verlet積分[8-11]方法計算速度快，精度高，簡單穩(wěn)定，故選用Verlet積分方法進(jìn)行微分方程的數(shù)值求解。

(6)

將式(5)代入式(6)得：

x(t+Δt)=2x(t)-x(t-Δt)+

(7)

式中：x(t)為當(dāng)前質(zhì)點在t時刻的位置矢量；Δt為迭代時間步長；F(t)為當(dāng)前質(zhì)點所受到的合力。上式表明，由質(zhì)點當(dāng)前時刻t和前一時刻的位置矢量和受力情況可預(yù)測該質(zhì)點下一時刻的位置。

2.2 織物網(wǎng)格變形實現(xiàn)

求解彈簧-質(zhì)點模型獲得質(zhì)點在一定時間后的位置，圖1(b)示出初始狀態(tài)的彈簧-質(zhì)點模型在力的作用下最終形成圖1(c)所示的織物網(wǎng)格變形圖。在圖1(b)示出的織物二維網(wǎng)格變形圖中，內(nèi)層密度大的組織其變形趨勢是向周圍擴(kuò)散的，外層密度小的組織有往中間收縮的趨勢，且其變形程度比緊密組織的稍大，符合密度大的組織更加穩(wěn)固的實際情況。整個織物中變形最大的部分是發(fā)生在2個組織交接處，越遠(yuǎn)離組織交接處，線圈變形程度越小甚至沒有變形。織物網(wǎng)格變形圖代表了織物的變形趨勢。

3 線圈-網(wǎng)格模型

為使織物外觀模擬更具真實感，采用NURBS曲線描述線圈形態(tài)；建立二維網(wǎng)格質(zhì)點與線圈曲線控制點之間的關(guān)聯(lián)式，定義其為質(zhì)點-控制頂點關(guān)聯(lián)式。由質(zhì)點坐標(biāo)和質(zhì)點-控制頂點關(guān)聯(lián)式計算出對應(yīng)曲線的控制頂點坐標(biāo)，由控制頂點生成相應(yīng)的NURBS曲線線圈，最終實現(xiàn)對整個織物的線圈建模。

3.1 NURBS線圈模型

3.1.1 NURBS曲線

在針織物的線圈仿真模型中，NURBS曲線[12]的形態(tài)可通過控制頂點實現(xiàn)局部調(diào)控，因此不會因單個控制頂點的改變引起整條曲線形態(tài)都發(fā)生改變，形態(tài)更加可控。基于此，本文采用NURBS曲線進(jìn)行線圈形態(tài)模擬。

k次非均勻有理B樣條曲線(k次NURBS)表達(dá)式[13]為

(8)

式中：Pi為控制頂點，構(gòu)成控制多邊形；ωi>0為權(quán)因子，確定控制(頂)點的權(quán)值，其值越大，曲線越接近相應(yīng)的控制點，這里取ωi=1，k=3,u=[u0,u1,…,un+k+1]為節(jié)點矢量，節(jié)點矢量首末取四重節(jié)點即u0=u1=u2=u3=0，un+1=un+2=un+3=un+4=1，內(nèi)節(jié)點u4,u5,…,un采用里森費(fèi)爾德方法[14]確定；Ni，k(u)為定義于非均勻控制矢量上的k次B樣條基函數(shù)。

3.1.2 選取線圈模型控制頂點

本文在如圖8(a)所示二維Peirce線圈模型[15]基礎(chǔ)上選取線圈的NURBS曲線控制頂點，在矩形單元格中選取圖8所示10個點Pi(i= 0,1,…，9)，作為三次NURBS曲線線圈的控制頂點，形成如圖8(b) 所示的的NURBS線圈。其中，虛線部分為控制多邊形，實線部分為1個NURBS曲線線圈，P0P1P2、P7P8P9段控制線圈的沉降弧形態(tài)，P2P3、P6P7段控制圈干形態(tài)，P3P4、P5P6段控制針編弧形態(tài)。

圖9示出了縱向線圈之間相互串套關(guān)系，其中黑色實線代表當(dāng)前線圈，Mj(j=1,2,3,4)為質(zhì)點，Pi(i=0,…,9)為NURBS曲線(控制頂點)。控制頂點Pi(i= 0,1,…，9)的坐標(biāo)為

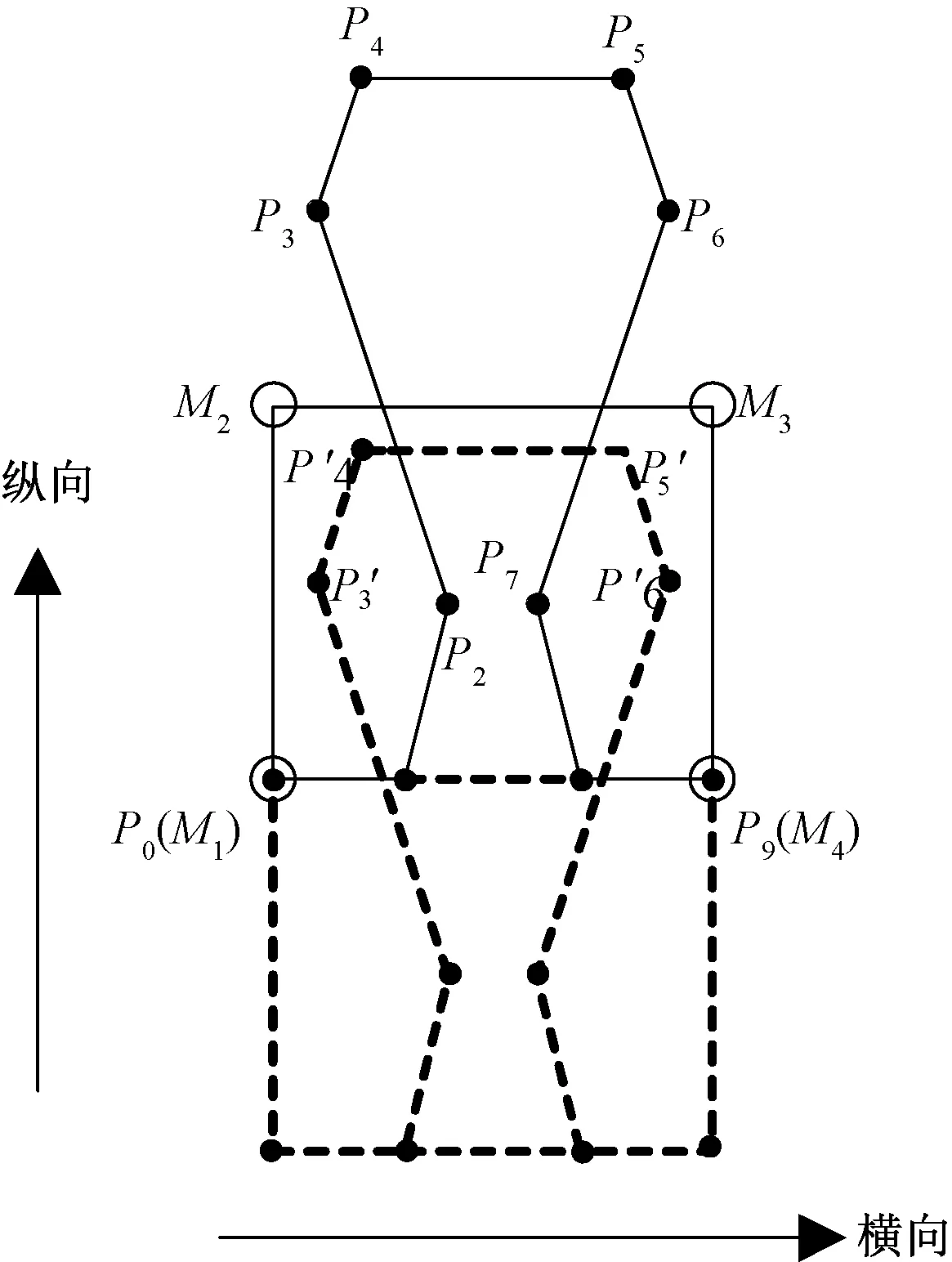
圖9 線圈縱向串套關(guān)系示意圖Fig.9 Diagram of longitudinal cascade relationship of loops

pi=kx,iAx+ky,iBy,i∈[0,9]

(9)

式中：x，y分別為x、y方向的單位向量；矩形網(wǎng)格寬度A為圈距；高度B為圈高；kx,i,ky,i分別為當(dāng)前控制點與A，B的比例系數(shù)，其取值詳見表1，其中系數(shù)大于1的點在由Mj(j=1,2,3,4)構(gòu)成的矩形單元格的外部，小于1的點在矩形單元格的內(nèi)部。

3.2 質(zhì)點-控制頂點關(guān)聯(lián)式

建立質(zhì)點與控制頂點的數(shù)學(xué)關(guān)系式[1,15]，由質(zhì)點-控制頂點關(guān)聯(lián)式和質(zhì)點坐標(biāo)就可計算出控制點坐標(biāo)，將控制頂點代入式(8)生成相應(yīng)的NURBS曲線線圈，如圖10所示。控制點用來控制線圈的幾何形狀，質(zhì)點控制四邊形的形狀，當(dāng)質(zhì)點受力偏移，四邊形發(fā)生變形；相應(yīng)的NURBS曲線線圈也發(fā)生變形,如圖10(b)所示。每個單元格的4個質(zhì)點關(guān)聯(lián)1個線圈的10個控制頂點。

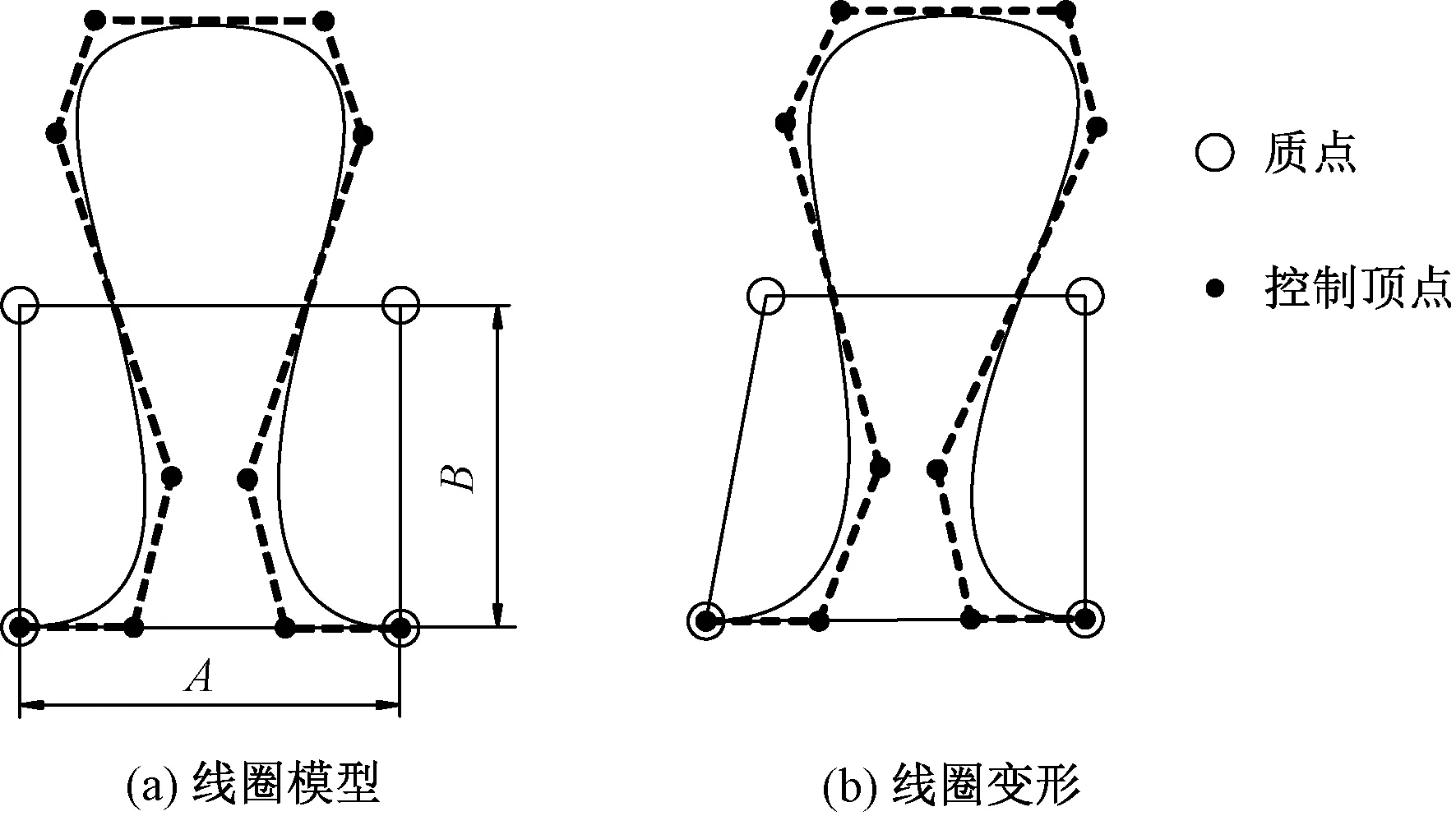
圖10 線圈-網(wǎng)格模型Fig.10 Loop-mesh model.(a) Ideal style of loop;(b) Deformed loop

結(jié)合表1，將控制頂點Pi(i=0,…,9)用質(zhì)點Mj(j=1,2,3,4)線性表示,用矩陣相乘形式表示即

表1 線圈控制點比例系數(shù)取值表Tab.1 Value of scale factor of control point of loop

(10)

式中：P=[P0,P1，…,P9]；M=[M1,M2,M3,M4]。

按行、按列遍歷網(wǎng)格變形圖中每一個單元格，依次用NURBS曲線線圈取代每個四邊形單元格，最終形成整個織物的變形仿真圖，如圖1(e)所示，其為圖1(c)所示網(wǎng)格變形圖對應(yīng)的變密度非均勻變化的織物變形模擬圖。

4 實驗與織物仿真效果分析

4.1 織物樣品

設(shè)計實驗，將真實織物與其對應(yīng)的仿真圖對比，分析仿真結(jié)果的可靠性。

為減少干擾因素，所有樣品采用相同的紗線原料：39.37 tex×7腈綸，樣品由慈星電腦橫機(jī) CE2-60S 編織而成，實驗設(shè)計了如圖11所示2種樣式的織物樣品。其中圖11(a)所示樣品由3種密度的平針組織組成，從上往下分別為平針組織1(紫色)、平針組織2(藍(lán)色)、平針組織3(綠色)；圖11(b) 示出的樣品由2種密度的平針組織組成，從里到外分別是平針組織2(藍(lán)色)、平針組織3(綠色)。樣品具體參數(shù)詳見表2。

圖11 樣品實物圖Fig.11 Physical picture of sample.(a) Sample 1;(b) Sample 2

表2 織物規(guī)格參數(shù)表Tab.2 Fabric specification parameters

4.2 計算機(jī)織物仿真及效果分析

使用javascript進(jìn)行數(shù)據(jù)處理和計算，使用SVG進(jìn)行圖形繪制，對樣品1、2進(jìn)行仿真,仿真的部分信息見表3。仿真圖如圖12所示。

圖12 樣品仿真圖Fig.12 Simulation diagram of sample.(a) Sample 1；(b) Sample 2

表3 計算機(jī)織物仿真的部分信息表Tab.3 Partial information of fabric simulation on computer

計算機(jī)織物仿真算法流程如下。

輸入：織物各組織的橫列數(shù)、縱行數(shù)、圈距、圈高等參數(shù)。

輸出：織物線圈仿真圖。

步驟1：初始化織物彈簧質(zhì)點模型的質(zhì)點坐標(biāo)。

步驟2：遍歷所有質(zhì)點，對質(zhì)點進(jìn)行受力分析。

步驟3：建立質(zhì)點的力學(xué)微分方程，并使用數(shù)值方法求解方程，得到質(zhì)點在力的作用下一個時間步長的位移，更新質(zhì)點位置。

步驟4：重復(fù)步驟2、3，當(dāng)所有質(zhì)點相比上一次迭代，其位移量不大于設(shè)定的極限值時，停止迭代。

步驟5：將質(zhì)點位置代入質(zhì)點-控制頂點關(guān)聯(lián)式，得到控制頂點位置。

步驟6：根據(jù)控制頂點確定NURBS曲線，顯示織物仿真圖。

對照圖11樣品實物圖與圖12中相應(yīng)的仿真圖分析知，仿真圖與實物圖變形趨勢是一致的，整體尺寸也基本保持一致。變形程度最大的線圈主要集中在不同密度的組織交接處，遠(yuǎn)離組織交接處的線圈變形程度逐漸變小,且織物外輪廓處變形和實際織物的卷邊也保持一致。

5 結(jié)束語

根據(jù)織物密度分布圖建立織物彈簧-質(zhì)點模型，對模型中質(zhì)點進(jìn)行受力分析并建立微分方程，采用Verlet數(shù)值積分求解方程，形成織物網(wǎng)格變形圖，在此基礎(chǔ)上結(jié)合NURBS曲線線圈模型，形成密度非均勻分布緯編針織物仿真圖，對比仿真圖與實際樣品，變形趨勢高度一致。研究為密度非均勻分布的緯編針織物的變形研究提供了一種解決思路，對設(shè)計者預(yù)測密度非均勻分布的緯編針織物成品最終外觀形態(tài)有一定的參考價值。但本文織物組織的組合樣式比較少，另外涉及到織物中大量線圈的變形問題時，仿真模擬的計算效率也是值得關(guān)注的問題，本文仿真的計算效率還有待提升。

FZXB