思維巧突破，零點妙證明
——2020年全國卷Ⅲ(理)第21題

劉宇峰 (江蘇省張家港中等專業學校，江蘇 張家港 215600)

利用導數破解函數零點的相關問題一直是歷年高考中比較常見的一類題型，其創意新穎，背景各異，場景各不相同，思維方法變化多端．此類問題，合理地將函數、函數的零點、不等式以及導數及其應用等相關問題加以合理交匯，巧妙破解，方法多樣，思維多變，為各層次的學生均提供相應的切入機會，具有很強的高考區分度與選拔性，是高考命題者青睞與熱衷的一個命題方向.

一、真題呈現

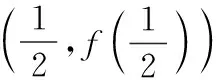
(1)求b；

(2)若f(x)有一個絕對值不大于1的零點，證明：f(x)所有零點的絕對值都不大于1.

此題以含參的三次函數為問題背景進行合理創設，以導數的幾何意義、函數的零點等來合理設置，是高考中考查函數與導數應用的交匯與融合時比較常見的函數類型.通過創新形式，利用導數的幾何意義來合理構建，進而確定相應的參數值，并在此基礎上，通過函數對應的一個零點的性質，結合函數的零點的取值情況來巧妙設置證明問題，難度較大，讓人眼前一亮，同時很好地考查了數學基礎知識、數學思想方法和數學能力等，具有很好的區分性與選拔性.

二、真題破解

解析：(1)f′(x)=3x2+b，

(2)思維視角一：分類討論思維

方法1：(分類討論法)

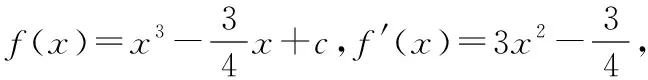
而導函數f′(x)與函數f(x)的情況為：

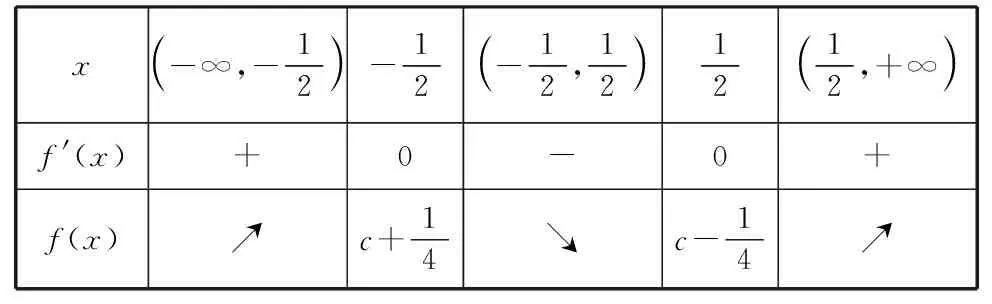
x-∞,-12 -12-12,12 1212,+∞ f '(x)+0-0+f(x)↗c+14↘c-14↗

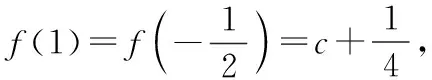
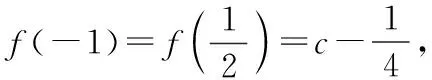
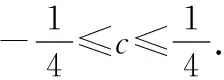
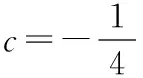
綜上，若函數f(x)有一個絕對值不大于1的零點，則函數f(x)所有零點的絕對值都不大于1.

點評：根據題目條件，先求導，結合導函數的正負取值情況、函數的單調性、函數在極值點處的取值情況，對參數c分類討論，再利用函數的不同零點個數情況加以分類討論，從而證明相關的命題成立.

思維視角二：參數分離思維

方法2：(反解參數法)

設x0為函數f(x)的一個零點，根據題意，

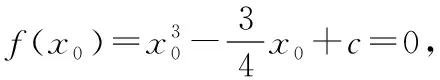
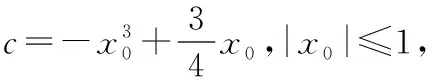
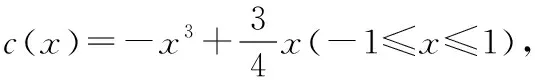
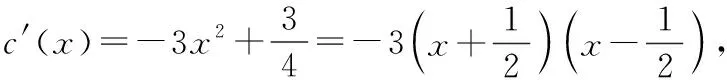
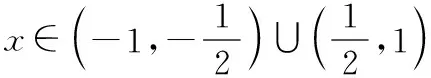
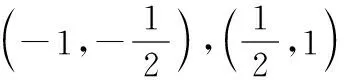
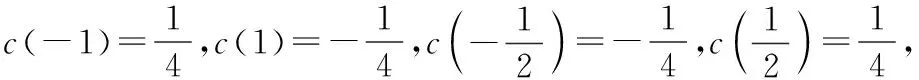
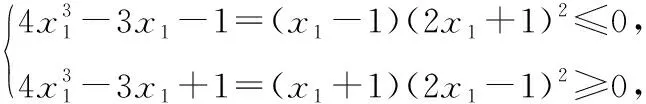
所以函數f(x)所有零點的絕對值都不大于1.

點評：根據題目條件，分離參數，通過構造函數，求導，利用函數的單調性以及函數值來確定參數的取值范圍，結合函數零點所滿足的關系式，利用不等式組的建立與求解來確定零點的取值范圍，從而證明相關的命題成立.

思維視角三：因式分解思維

方法3：(作差分解法)

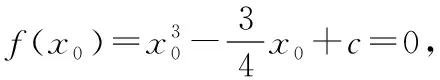
若函數f(x)只有一個零點，則問題得證；

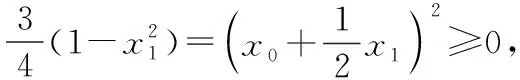
綜上，若函數f(x)有一個絕對值不大于1的零點，則函數f(x)所有零點的絕對值都不大于1.

方法4：(待定系數法)

否則，可設函數f(x)=(x-x1)(x-x2)(x-x3)，

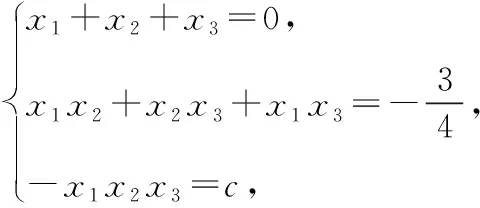
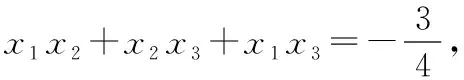
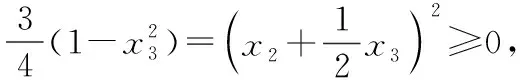
在柔性垂直防滲技術實施完成后，對調節池內滲瀝液和監測孔內地下水進行取樣檢測，檢測結果表明柔性垂直阻隔系統對污染物的阻隔作用明顯。檢測結果見圖5。

同理可得|x1|≤1，|x2|≤1，問題得證.

綜上，若函數f(x)有一個絕對值不大于1的零點，則函數f(x)所有零點的絕對值都不大于1.

方法5：(判別式法)

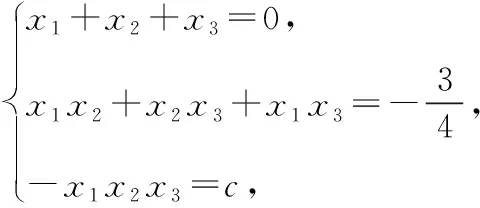
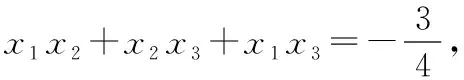
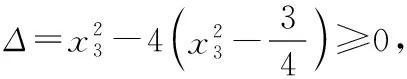
同理可得|x1|≤1，|x2|≤1，問題得證.

綜上，若函數f(x)有一個絕對值不大于1的零點，則函數f(x)所有零點的絕對值都不大于1.

方法6：(二次函數法)

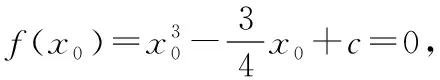
若函數f(x)只有一個零點，則問題得證.

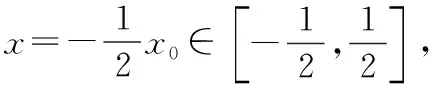
結合二次函數的圖像與性質可知g(x)=0的兩根均在[-1，1]內，即g(x)=0的兩根絕對值不大于1，問題得證.

綜上，若函數f(x)有一個絕對值不大于1的零點，則函數f(x)所有零點的絕對值都不大于1.

點評：根據題目條件，分函數f(x)只有一個零點或其他情況，利用函數零點的性質因式分解，借助相關零點關系式加以作差分解、待定系數、函數與方程以及構造函數轉化法等思維，證明零點的絕對值不大于1即可證明相關的命題成立.

思維視角四：三角函數思維

方法7：(三角換元法)

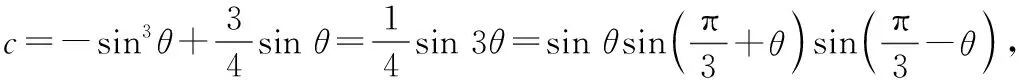
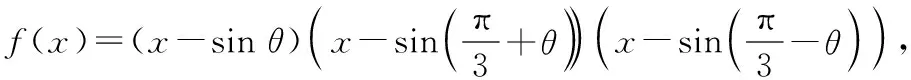
若函數f(x)只有一個零點，則問題得證；

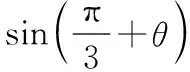
問題得證.

綜上，若函數f(x)有一個絕對值不大于1的零點，則函數f(x)所有零點的絕對值都不大于1.

點評：根據題目條件，設出函數f(x)的絕對值不大于1的零點的三角關系式，分離參數，借助三倍角公式以及三角恒等變換公式的轉化，確定函數的三角關系表達式，分函數f(x)只有一個零點或其他情況，結合三角函數的圖像與性質來證明相關的命題成立.

思維視角五：反證思維

方法8：(反證法)

令f′(x)>0，

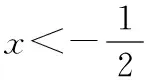
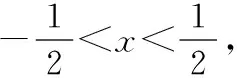
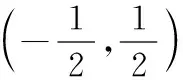
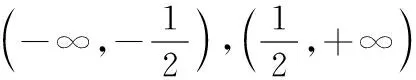
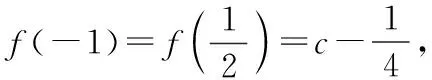
若函數f(x)所有零點中存在一個絕對值大于1的零點x0，

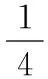
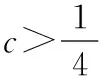
又f(-4c)=-64c3+3c+c=4c(1-16c2)<0，

由零點存在性定理知函數f(x)在(-4c，-1)上存在唯一一個零點x0，

即函數f(x)在(-∞，-1)上存在唯一一個零點，在(-1，+∞)上不存在零點，

此時函數f(x)不存在絕對值不大于1的零點，與題設矛盾；

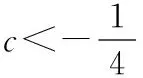
又f(-4c)=-64c3+3c+c=4c(1-16c2)>0，

由零點存在性定理知函數f(x)在(1，-4c)上存在唯一一個零點x0′，

即函數f(x)在(1，+∞)上存在唯一一個零點，在(-∞，1)上不存在零點，

此時函數f(x)不存在絕對值不大于1的零點，與題設矛盾.

綜上，函數f(x)所有零點的絕對值都不大于1.

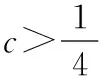
三、變式拓展

【變式】(2022屆云南省大理州大理市高三(上)月考數學試卷)設函數f(x)=aex(x-1)-2x2+b.

(1)討論f(x)的單調性；

(2)若a=2，f(x)有一個不大于0的零點，證明：f(x)所有的零點都不大于1.

分析：(1)求出導函數，然后分a≤0，04，結合導數的正負與函數單調性的關系求解即可；

(2)由題意，f(0)=b-2≥0，分別利用零點的定義證明b=2，b>2時函數的單調性，對f(ln 2)與0的大小關系進行討論即可.

點評：本題考查了利用導數研究函數的單調性，導數與不等式的綜合應用.在利用導數證明涉及函數零點的不等式問題時，一般會構造一個函數，通過分類討論思想、函數與方程思想等的應用，轉化為求解函數的取值情況，考查了邏輯推理能力與化簡運算能力，以及對應的數學思想方法，屬于難題.

四、解后反思

在解決此類利用導數來破解函數零點的相關問題時：可直接利用函數特征加以分類討論；可直接構造相應的函數合理轉化；可直接通過導數來確定對應函數的草圖，數形結合；可間接通過設置結論的反面加以反證推理，以達到解決問題的目的．在破解問題時無論采用何種方法切入，都離不開相應參數的分類討論與函數單調性、極值與最值的應用，關鍵是熟練掌握基本題型和基本破解方法與策略，以不變應萬變.