化歸與轉化思想在數學教學中的作用探討

鄧玉蘭

化歸與轉化思想在數學教學中的作用探討

鄧玉蘭

（蘭州市第六十一中學，甘肅蘭州730060）

化歸與轉化是一種重要的數學思維方式，甚至是其他數學思想方法的核心。掌握了化歸與轉化思想，不但能夠引導學生更好地學習數學知識、解決數學問題，還能夠使學生在其他學科的學習和生活實際問題的解決中得心應手。

化歸與轉化思想；數學教學；作用

數學思想是數學活動中“教與學”的靈魂，作為建立和運用數學解決問題的指導思想，它指引著學習者和教學者順利完成在數學“教與學”中的各項工作和任務。由于數學領域的問題千姿百態，所以衍生出了多種不同的數學思想方法，用于指導數學知識的教與學。

一、化歸與轉化思想簡介

化歸與轉化思想就是這五彩繽紛的數學思想方法世界中最耀眼的一顆星，錢佩玲老師也稱化歸與轉化思想是數學中問題解決的基本方法。首先化歸與轉化思想符合學生的認識規律；其次數學學科自身的特點和數學科學的哲學基礎，決定了化歸與轉化思想的數學地位——數學解決問題的基本方法。

“化歸”一詞其實就含有轉化的意思，但是，其最終目的是將一個問題歸結為另外一個方便于解決的問題。基本思想是：在數學問題的解決過程中，人們通常會把需要解決的問題M，經過某種轉化的方法，將其變換為另外一個已經解答或者已經有固有的解決程序的數學問題N，并且通過解決問題N，進而可以解決原問題M。這樣一個化歸的過程通常可以用下面的框圖簡單表示：

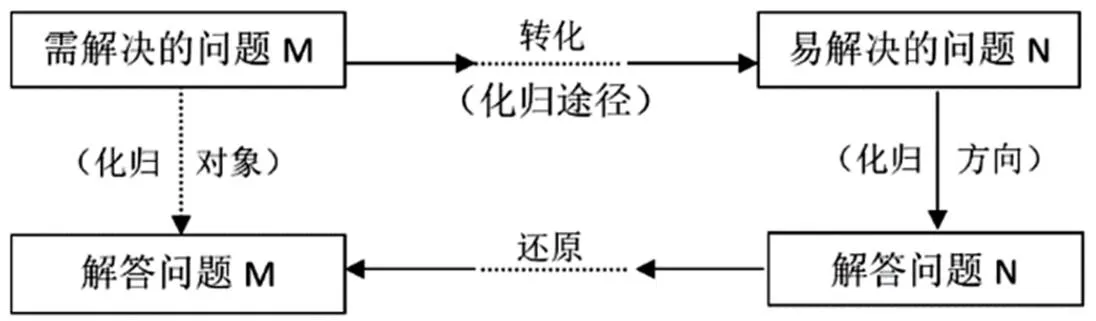
圖1

如圖1中標示的，問題N經常被稱作化歸與轉化的方向或目標，化歸與轉化的方法就是轉化，經常被稱作化歸與轉化的策略。化歸的方向有時可能是將煩瑣的問題化成單一的問題，有時是將未知的問題化成已知的問題，有時是將不能解答的問題化成已經解答的問題等，有時并不是一步就能完成化歸與轉化，需要經過好幾步才能完成。也就是說將原來的問題M，通過轉化途徑，轉化為問題M1，再將問題M1轉化為問題M2，按照“化難為易，化繁為簡，化未知為已知”的基本原則繼續進行轉化，直至將其轉化為問題N，然后一步一步地還原解答每一個問題，直至解答原問題M。如此一來，上面框圖又可以呈現為更一般的化歸模式，圖2：

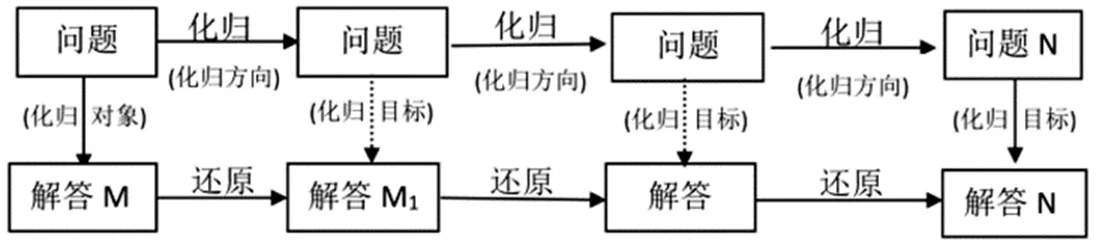
圖2

由此可以看出化歸與轉化思想符合“小步子教學”的原則，把較復雜難以解決的問題，不如就稱其為“大問題”，轉化為一個個比較容易解答的“小問題”，各個擊破，最終回歸到原問題，解決一開始的“大問題”。也有人將化歸與轉化思想稱為是一種“迂回前進”的方法，而其最終的目的是“回到老家”，解答原始的問題。

據說，從研究數學思想方法中可以看出一個重要的問題，那就是與一般的科學家（如化學家）相比，數學家具有其特殊的地方，那便是在數學思想方法這一方面，因為數學家具有重要的思維特點——他們善于利用化歸與轉化的思想解決問題。這也就更加突出了，化歸與轉化思想方法在數學思想方法中的重要地位。

二、化歸與轉化思想在數學教學中的作用

在數學教學的每一個階段、每一個環節化歸與轉化思想都具有指導意義，并且是眾多數學思想方法的基礎，比如說數形結合思想、函數與方程思想、一般與特殊的思想等。其在中學數學中的主要作用有：

1.運用化歸與轉化思想指導新知識的形成

比如《分數乘整數》《兩平行線間距離公式》的可以用等價轉化法去講解，《集合的基本運算》《平明向量的坐標表示及坐標運算》的講解可以充分地利用數形結合的思想講解等，這些案例都體現了化歸與轉化思想對新知識形成的指導作用。

2.利用化歸與轉化思想引導問題的解決

問題解決是數學“教”與“學”活動的核心，新知識的講解也是為問題的解決提供依據和新的方法。化歸與轉化思想其實是通過轉化的方法，將未知的問題轉化為已知的問題，將陌生的問題轉化為熟悉的問題，將煩瑣的問題轉化為單一的問題等。轉化的方法也是多種多樣，比如，數形結合法、特殊化的方法、正反轉化的方法等。但是方法再多，其核心的思想就是簡化問題，不要用靜止的態度看待問題，而是要用變化的態度看問題，學會變通。

師：復合函數求值域，不做變換直接求比較復雜。觀察到根號下的內容是二次式，可以聯想到配方法，進行相應的轉化后大家再觀察該式。

生：

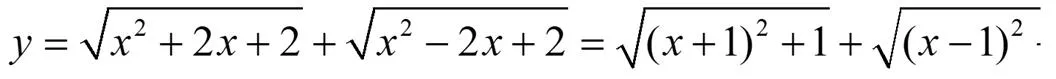
師：很好，還可以繼續轉化嗎？想一想兩點間的距離公式。

生：

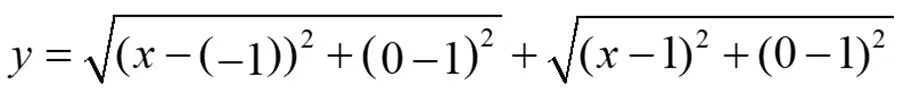
生：解：因為

師：很好，這道題的主要思想是數形結合，通過換元法把函數的值域問題轉化為動點到定點的距離和的最值問題。

利用化歸與轉化思想的熟悉化原則、簡單化原則以及和諧化原則解數學題，能夠引導學生進行正確的思維活動，使之能夠順利解決問題。

3.利用化歸與轉化思想進行知識結構的梳理

每次學完一節或一章內容的時候，都應進行知識點的梳理和總結。梳理過程中可以消化、提煉、整理知識，系統化地記憶知識，把零零碎碎的知識組織成井然有序的、層次分明的知識地圖，將課本知識學薄，提綱挈領，更容易記憶、理解和利用。

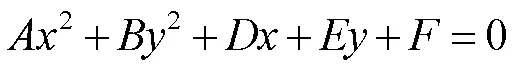
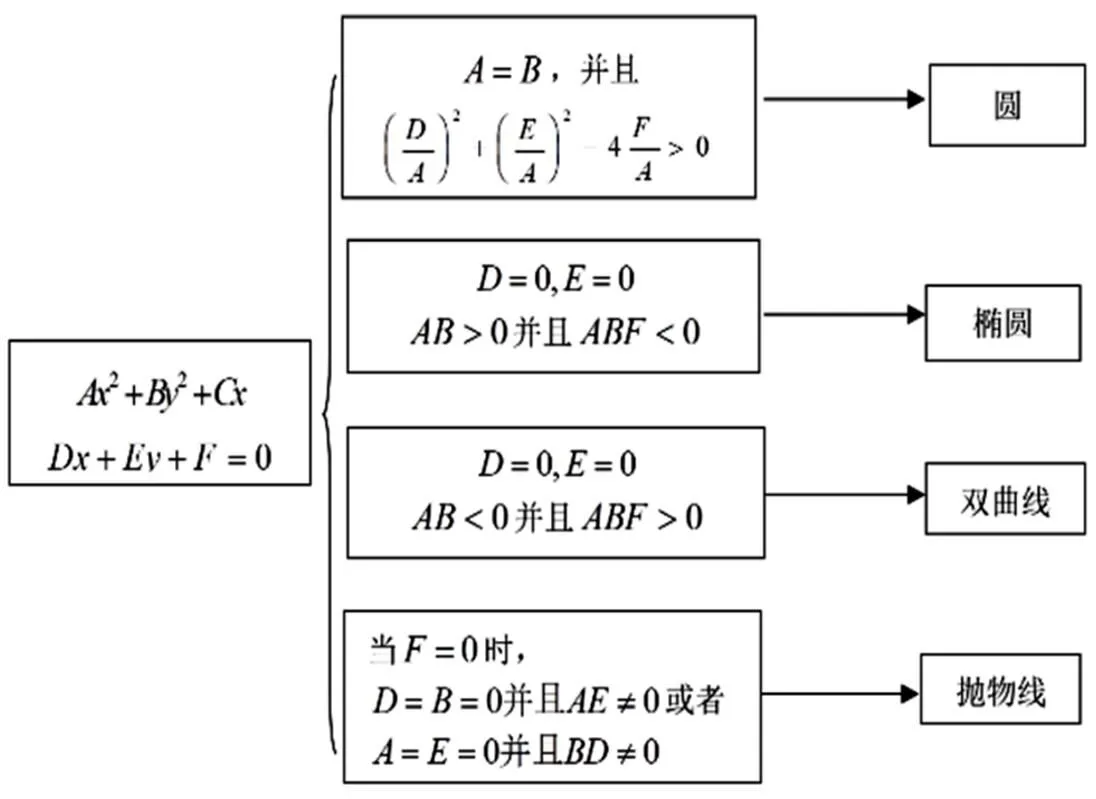
圖3

三、在數學教學中進行化歸與轉化應該注意的問題

化歸與轉化思想作為問題解決的基本方法，其進行轉化的方法可謂是多種多樣。恩格斯和馬克思的辯證唯物主義告誡后人：“世界永遠都是處于運動與變化之中的，要用辯證的態度去看待一切。”所以在利用化歸與轉化思想的時候，不能將思維局限于某一具體的方法，而是要用動態變化的觀點分析問題、解決問題。在化歸與轉化的過程中應該注意：

1.有目的、有意識地介紹和突出化歸與轉化，找準目標

有目的、有意識地介紹和突出化歸與轉化，緊緊“鎖住”目標，利用化歸與轉化的原則，將題目化生為熟，化難為易；進行規范化、高效化的化歸與轉化。

在教學中，首先，教師應該根據學生的數學學習和教學內容，考慮突出介紹化歸與轉化思想環節，學生把握化歸與轉化思想的層次。其次，對每一個教學環節要合理的設計，精心的安排，有意識、有目的地進行化歸與轉化的教學。

化歸與轉化思想包括化歸與轉化的對象、目標以及途徑和方法（如圖4）。因此，在化歸與轉化的過程中，應該明確化歸與轉化的對象，找準化歸與轉化的目標，選擇適當的化歸與轉化的途徑。目標是指引化歸與轉化前進的關鍵所在，所以要選準化歸與轉化的目標。選目標總是基于學生已有的數學知識進行的，根據學生已有的規范性知識，將學生遇到的問題規范化。除此之外，化歸與轉化能否順利進行還依賴于化歸與轉化的方法是否選擇的恰到好處，即要同時考慮目標和方法的可操作性、合理性和規范性。在解題的過程中緊緊地鎖住目標——原問題的解決，才能選擇合理恰當的方法，從而避免盲目地選擇方法，致使無法順利地完成問題的解答。

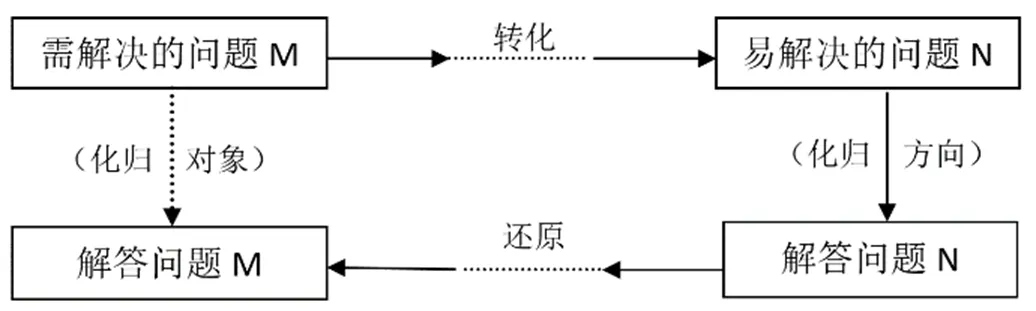
圖4

2.有計劃、有步驟地進行化歸與轉化，注意化歸與轉化的等價性

化歸與轉化大體上可以分為等價和非等價的化歸與轉化，但是中學階段的化歸與轉化大多數是等價轉化。因此在轉化的過程中要注意化歸與轉化的等價性。數學思想方法的教學是一個循序漸進的過程，在以上的案例中也有所體現，每一階段對于學生掌握化歸與轉化的水平要求是不一樣的，所以教學的過程中教師應該有計劃、有步驟地進行該思想方法的教學，而學生在學習的過程中應該花費時間實踐，不斷探索化歸與轉化思想暗含的玄機。

3.注意化歸與轉化方法的多樣性，設計合理方案，選擇最佳的方法

化歸與轉化的方法多種多樣，對于同一個問題就可以用多種不同的途徑實現，但并不是所有的方法都能簡化問題的解決方案，可能反而會使問題更加煩瑣，無論如何其中總有使問題最簡化的一種方法途徑，所以選擇最佳的方法是必要的。比如說下面的例題：

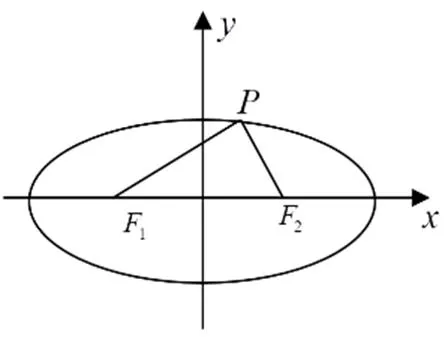
（A）點有兩個（B）點有四個

（C）點不一定存在（D）點一定不存在

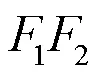
解法二：由圖可知，

不可能，所以選。

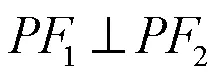
作為一名數學教師，應該加強訓練自己利用數學思想方法進行教學的能力，提高對數學思想方法的教學。在備課的時候應該豐富自己的教學目標，將數學思想方法的教學一并列入教學過程中，以輔助數學知識的講解。只有讓學生把握數學思想方法的真諦，才能將數學知識更好地納入自己的知識體系，加強自己的數學能力，終身受益，而作為教師也才能真正地做到“授學生以漁”。

[1] 錢佩玲.中學數學思想方法[M].北京:北京師范大學出版社,2010.

[2] 趙小云,葉立軍.數學化歸思維論[M].北京:北京科學出版社,2005.

[3] 朱廣俊.化歸思想及其在數學教學中的應用[J].江蘇第二師范學院學報(自然科學),2014,30(5):18-21.

[4] 袁健.化歸思想在初中數學教學中的運用[J].新課程,2010(10):28

[5] 朱成杰.數學思想方法研究導論[M].上海:文匪出版社,1998(6).

[6] 鮑怡.化歸思想方法在中學數學教育中滲透的案例研究[D].蘇州:蘇州大學,2009.

B038

A

1002-7661(2022)15-0058-03