借助GeoGebra對2020高考全國Ⅰ卷第21題的探究及拓展

?武漢大學附屬中學 齊黎明

1 問題的提出

(1)求橢圓E的方程；

(2)證明：直線CD過定點.

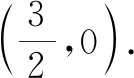
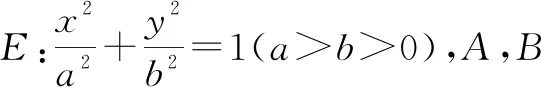
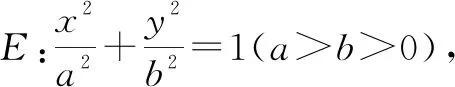
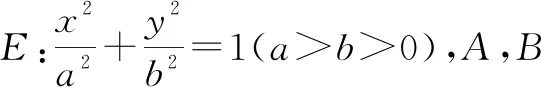
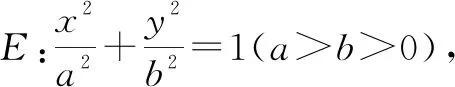
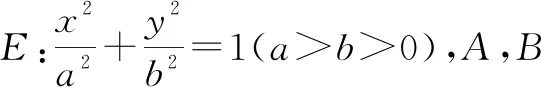
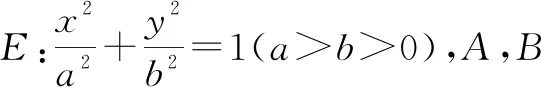
2 基于GeoGebra的探究

問題1～6將橢圓和點P一般化后，由于涉及運算比較復雜，判斷上述結論存在一定的難度.因此筆者借助GeoGebra進行探究，通過實驗演示觀察結論是否成立，同時為后面的代數證明提供了更加直觀、形象的思路支持.下面以問題1為例進行數學實驗探究.

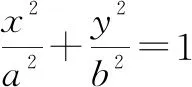
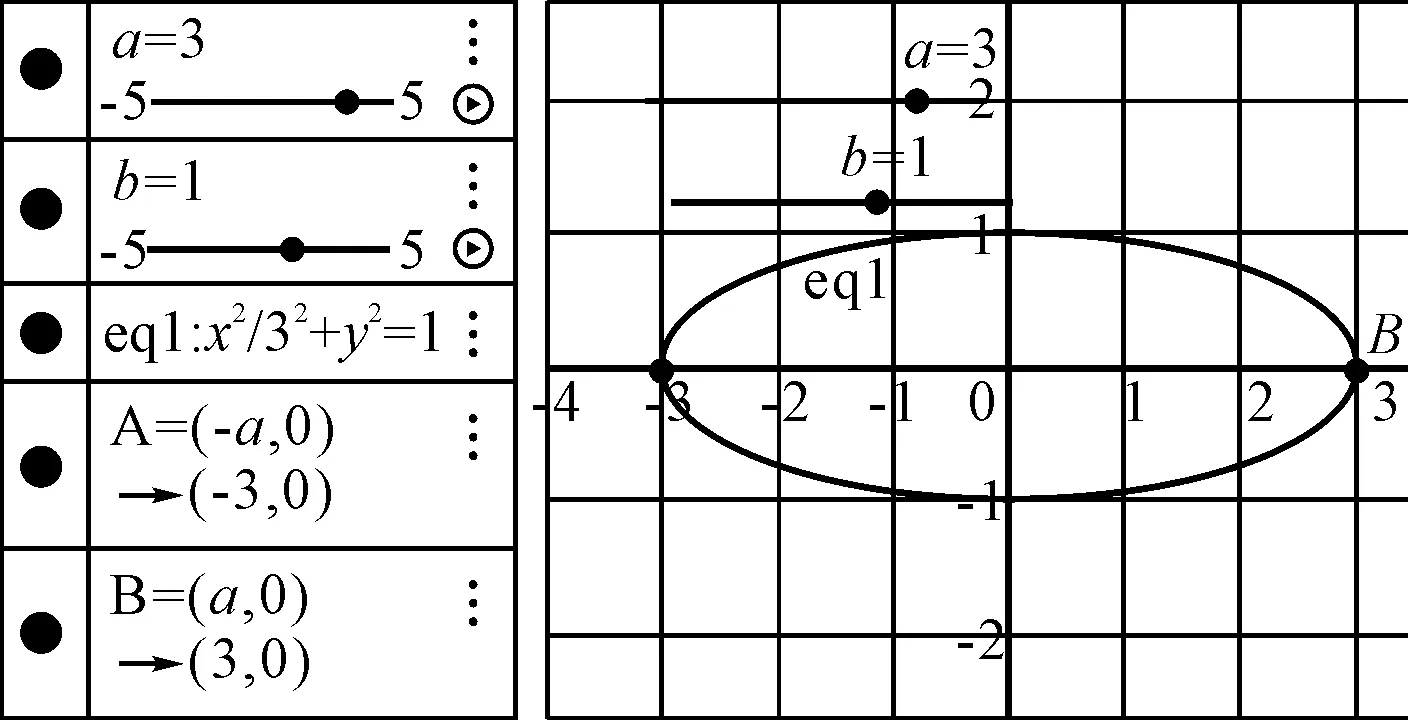
圖1

(2)設置兩個“滑動條”控制變量m,t，在輸入框中輸入直線x=m，輸入P=(m,t)，利用直線工具，作出直線PA，利用交點工具作出直線PA與橢圓E的交點C；繼續利用直線工具作出直線PB，利用交點工具作出直線PA與橢圓E的交點D，最后利用直線工具作出直線CD，利用交點工具作出直線CD與x軸的交點N，如圖2.

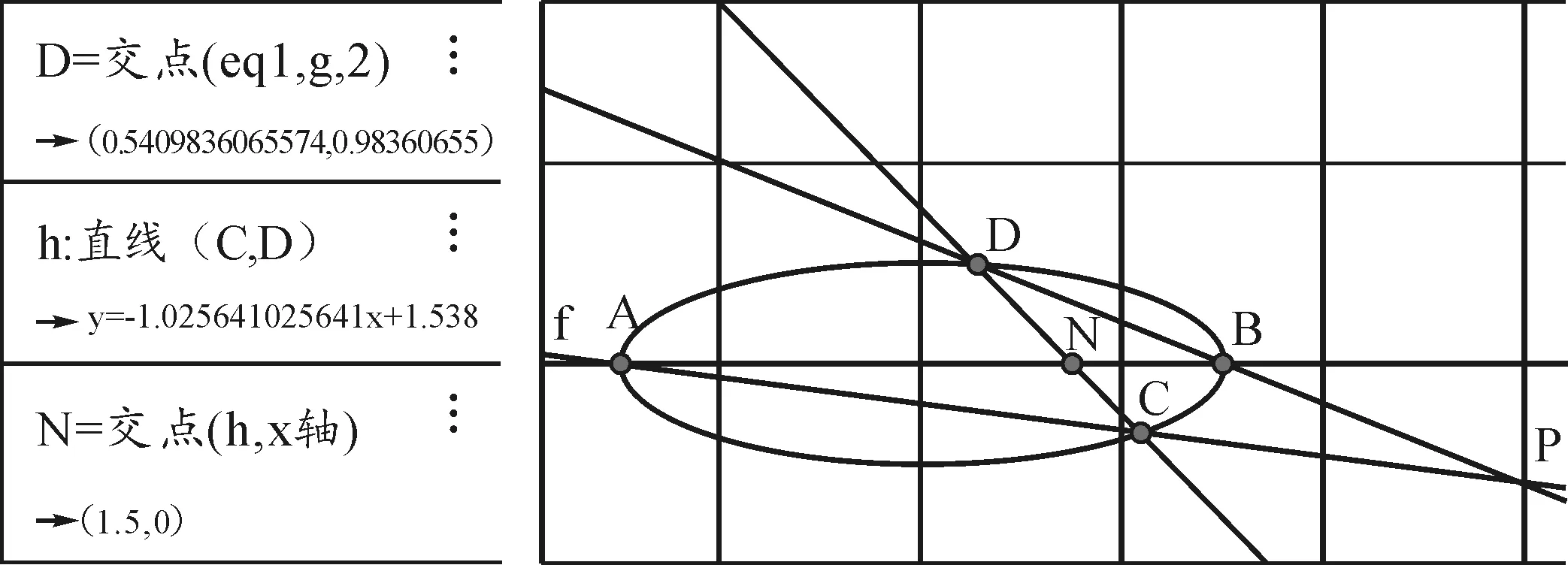
圖2

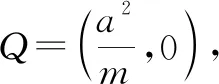
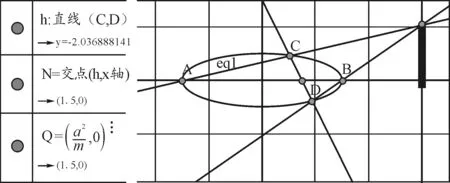
圖3

3 問題的拓展與證明

通過對以上問題的實驗探究，筆者將上述問題拓展到一般情形.

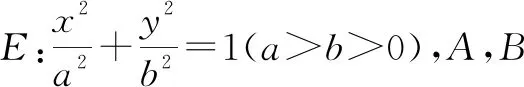
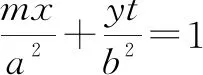
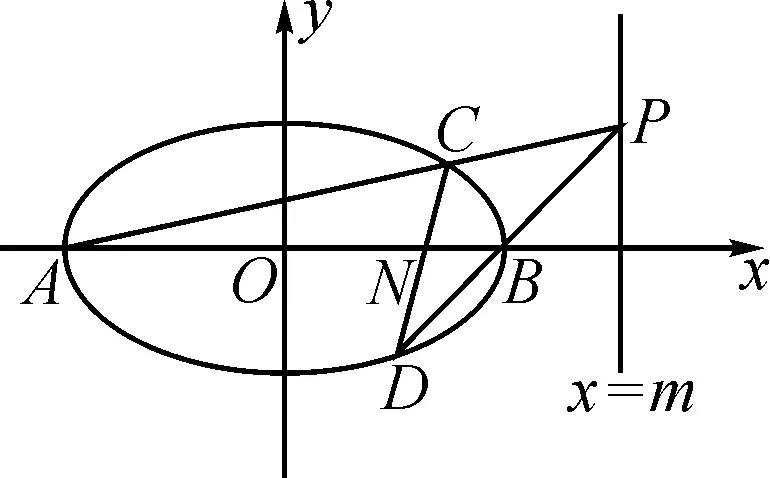
圖4

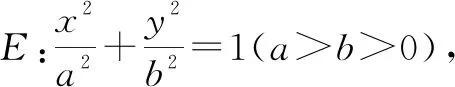
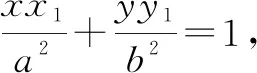
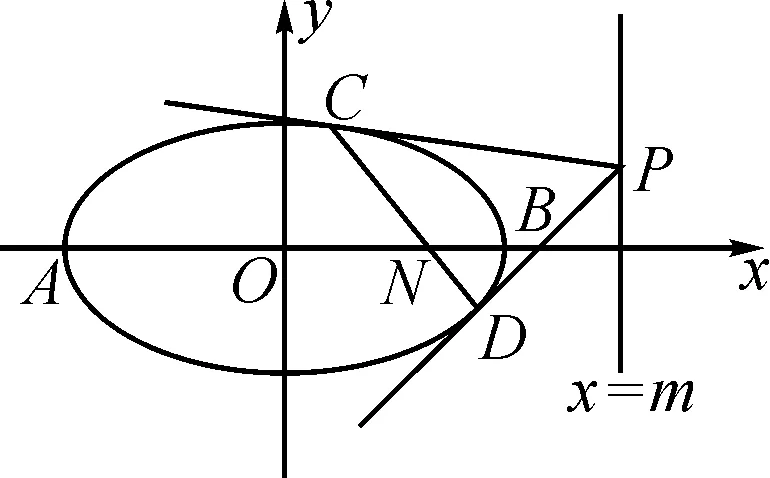
圖5

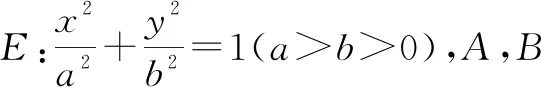
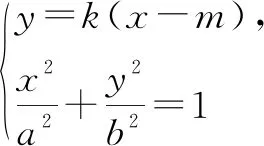
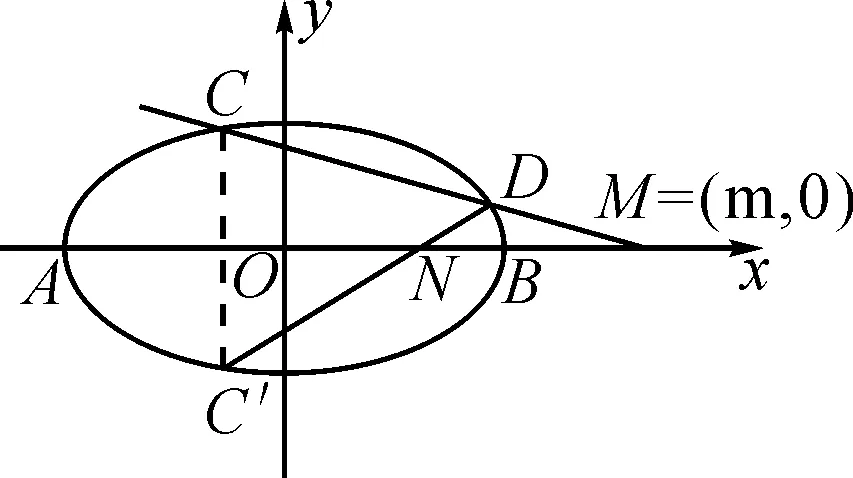
圖6

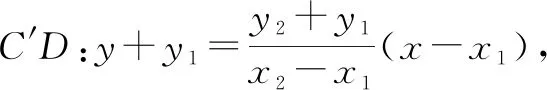
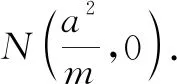
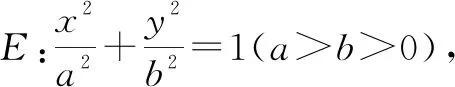
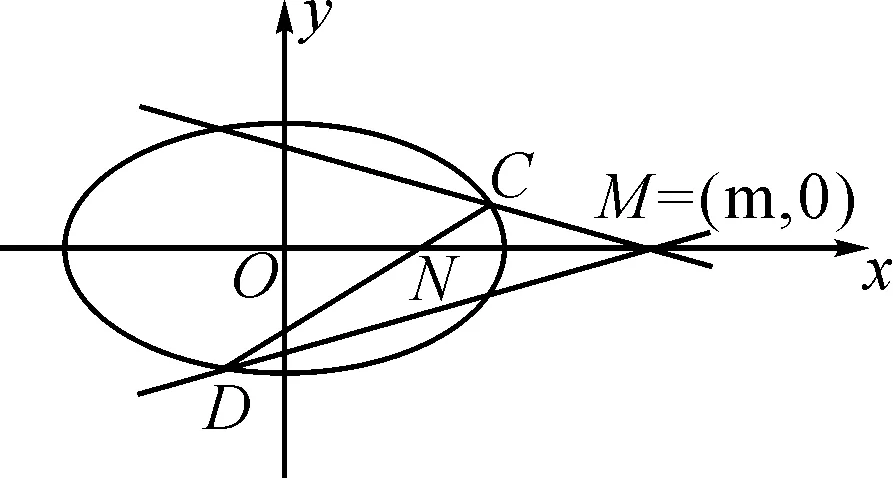
圖7

證明：可以轉化為結論3證明.

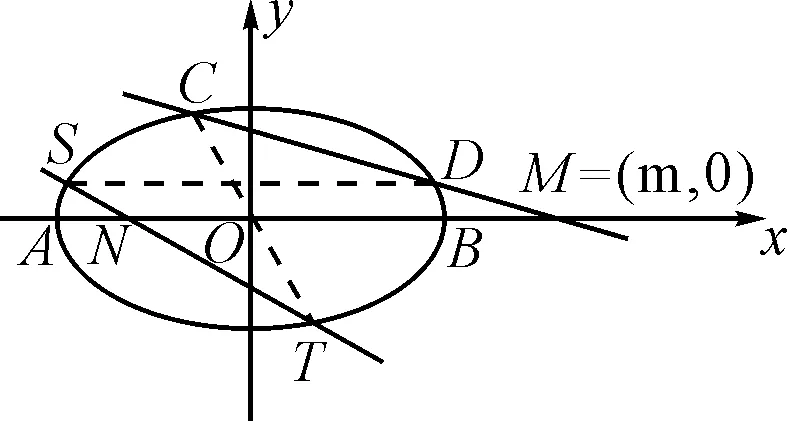
圖8

(a2k2+b2)x2+2kna2x+a2n2-a2b2=0，

令Δ>0，設S(x1,y1),T(x2,y2)，有

①

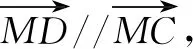
(m+x1)y2+y1(m+x2)=0，

化簡得 2kx1x2+(km+n)(x1+x2)+2mn=0

②

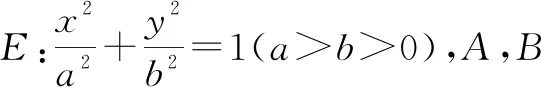
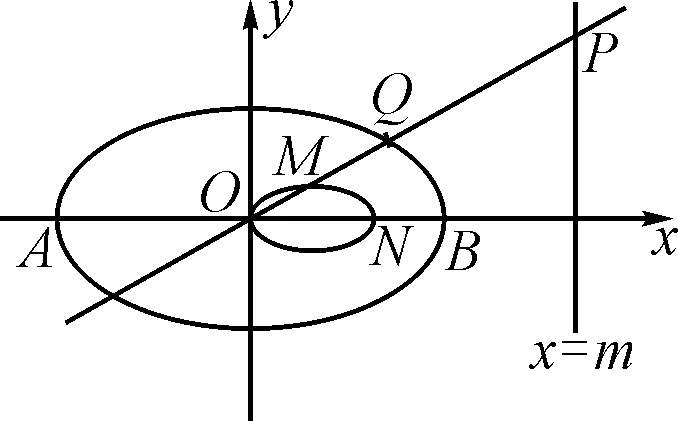
圖9

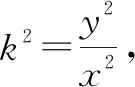
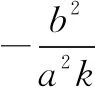
4 探究后的反思

在網絡互聯的背景下，信息技術在人們日常中的應用逐漸廣泛，并對數學教學產生了深遠影響.利用信息技術優化數學課堂教學，會起到事半功倍的效果.在本文的課堂實驗探究中，借助GeoGebra軟件，構建橢圓模型，通過控制變量不斷改變動直線和方程參數來演示圖形變化過程，讓學生觀察點的軌跡的運動情況，從而猜想出一般結論，為嚴謹的邏輯推理證明提供了實驗支持.在GeoGebra可視化動態實驗過程中，給學生搭建了一個探究直線過定點問題的平臺，結合題目中直線與橢圓的多元聯系，通過動態演示，把數與形之間的內在聯系進行直觀的表征，強化了數學知識間的聯系，加深學生的體驗，進一步揭示數學的本質，有助于激發學生學習數學的興趣，培養學生的自主探究能力，促進學生數學學科核心素養的提升[2].