“1”在數學解題中的妙用初探
?甘肅省天水市第九中學 陶建宏
1 引言
在解答數學題目時,經常會碰到一些覺得束手無策的情況,但通過仔細思考,不難發現題目中隱含的一個數“1”,若能發現這個數,將會收到意想不到的效果,下面通過幾個題目加以說明.
2 “1”的妙用
2.1 “1”在求三角函數值問題中的運用
例1已知tana=2求4sin2a-sinacosa-cos2a的值.
分析:這個題目如果由tana=2出發去求sina和cosa的值,再代入所求式子方可求出,但是在求sina和cosa的值時要分第一和第三象限兩種情況進行討論,并且在第一和第三象限sina和cosa的正負相同,在兩種情況下得到的答案相同,但作為一個解答題時必須分兩種情況進行計算.可是如果我們再好好觀察不難發現所求式子的分母是經常容易被人們忽視的“1”,而這里1=sin2a+cos2a再將分子分母分別除以cos2a,從而化為了正切的形式.
詳解:4sin2a-sinacosa-cos2a
注意:這里分母是“1”很少能引起人們的注意,以為沒有分母,而實質分母是容易被人們忽視的“1”.在三角函數部分多用1=sin2a+cos2a.
再比如,2007年全國高中數學聯賽河南省預賽(高二)中有這樣一道題目:已知7sinα+24cosα=25,則tanα=( ).
分析:對于此題如果能求出sina和 cosa的值,再利用商數關系可以求出tana的值,但是這很難求解.若對原式兩邊平方,再注意到sin2a+cos2a=1,得
(7sinα+24cosα)2=252×1=252[(sin2a+cos2a],展開整理得(24sinα-7cosα)2=0.
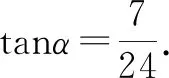
通過這兩個題目讓學生在三角函數化簡求值中注意這個很重要的數字“1”以及1=sin2a+cos2a.
2.2 “1”在指數、對數中的運用
在數學解題中,若能根據題目特征巧妙地利用“1”作代換,常能出奇制勝,取得較好解題效果.比如在指數和對數中經常會遇到一些有關“1”的問題.
例2解方程4x-2=1.
解析:因為a0=1(a≠0),所以4x-2=40,得x-2=0,即x=2.
看起來這是一個簡單的指數方程問題,但如果不知道a0=1(a≠0)這個條件,就無法更簡單求解.
例3解不等式lgx>1.
解析:因為logaa=1(a>0且a≠1) 所以lg10=1.又根據對數函數的單調性,由lgx>lg10,得x>10.
例4函數y=loga(x-4)的圖象恒過定點________.
解析:因為對數函數y=logax(a>0且a≠1)的圖象恒過點(1,0),由x-4=1,可得x=5.則函數y=loga(x-3)的圖象恒過定點(5,0).
指數函數與對數函數恒過定點是考試常考的一個知識點,它都涉及常數“1”.
通過這幾個題目可以看出在指數與對數中“1”顯得特別重要.要注意“1”這個特殊的數字,它的作用非常大,不能藐視.
2.3 “1”在求多元函數最值問題中的運用
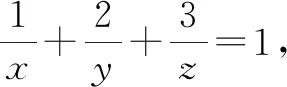
分析:這個題目是求多元函數最值的一個常見題目,學生剛開始覺得不好做,但若能靈活運用已知條件中的“1”作適當的整體代換,再利用均值不等式方可求解.
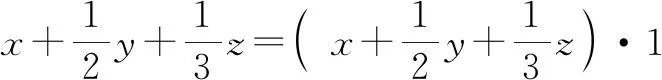
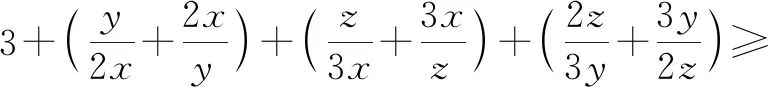
3+2+2+2=9,
當且僅當x=3,y=6,z=9時取得最小值9.
此題如果不能注意到“1”乘任意一個數都得這個數的話,這個題目就無法更簡單求解.
2.4 “1”在求多元條件下代數式的最值問題的運用
例6已知x>0,y>0且x3+y3=2,試求x+y的最大值.
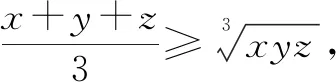
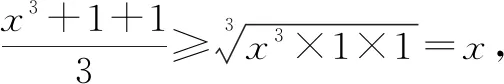
所以x+y的最大值是2,當且僅當x=y=1時取到最大值2.
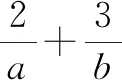
2.5 “1”在求無理式的最值問題中的運用
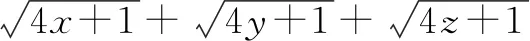
分析:解決這個題的關鍵是如何去掉根號,這樣才能利用x+y+z=1這個條件.在選修教材4-5中,學習了柯西不等式求最值,這個題就可以利用柯西不等式去求解.
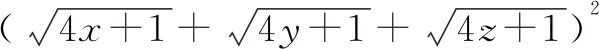
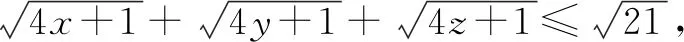
3 結束語
通過以上五類問題的典型例題,在求代數式的值或最值時,如果注意到“1”這個特殊數字,巧妙地利用“1”作代換,往往可以幫助我們把一個復雜的題目簡單化,從而達到事半功倍的解題效果.這里僅列舉了有針對性的七道例題,以達到拋磚引玉的目的.而實質上“1”這個簡單數字還有好多作用,這需要我們在平時的教學實踐中,做一個教與學的有心人,審題時要注意挖掘隱含條件,解題過程中要多做一些反思與總結,通過總結去加深理解并學以致用,從而提高解題能力、發散思維能力和探究歸納的能力.

